創設課堂質疑情境 引導學生構建學科素養
——以“對稱圖形”復習課為例

?廣東省廣州市第四十一中學 牛應林

“軸對稱”是人教版八年級數學上冊第十三章的內容，其中“對稱圖形”概念反映了數與形相互轉化的內在聯系.正是這一數學概念，溝通了代數運算和幾何性質，使得數學概念將數轉化為形、將形又轉化為數，“對稱圖形”就是對“數形轉換”的廣泛、深刻的解讀.因此，“對稱圖形”的復習課需要突出對數學基本概念的教學，但不等于就拋棄一般的數學知識，而是以最基本的數學概念為綱，以對數學概念的理解為目，在探究和拓展的過程中，不斷豐富知識的內涵與外延，綱舉目張，構建完整的數學學科素養.基于此，筆者以八年級上學期“對稱圖形”復習課為例，談談如何創設課堂質疑情境，引導學生構建學科素養.

1 以數學概念為核心，折射數學理論的基本內涵

在數學知識體系中，數學概念是最基本的出發點，也是數學知識體系進行拓展的依據.如“對稱圖形”的復習不僅有利于學生對數形轉換的認知和探究，更有利于學生在學習過程中將“軸對稱圖形”和“中心對稱圖形”體系化，而且對數與形的認識不只是停留在宏觀現象上，能夠更準確地從形的角度分析運算的規律，從而達到透過現象看本質的目的.同時，在“對稱圖形”概念形成的過程中，通過實踐探究和科學審美，能驅動學生的學習潛能，發展學生的邏輯思維能力，使學生的數學學科素養得到發展與升華.

在復習課整理知識體系的環節，筆者以導學案前置的方式，給出了“課前診斷”.

診斷:對稱美是美的一種重要形式，它能給人們一種圓滿、協調的美感，圖1中屬于中心對稱圖形的是( ).

圖1

質疑1:請說明你選擇的理由.

質疑2:另外幾個圖形有對稱特征嗎？若有，說明其是何種對稱圖形.

預設目的：在學生說明選擇中心對稱圖形的理由時，需要從“在平面內，把一個圖形繞著某個點旋轉180°，如果旋轉后的圖形能與原來的圖形重合，那么這個圖形叫做中心對稱圖形”出發，抓住其具備的特征；在完成質疑2時，同樣以軸對稱圖形的概念作為依據，分析圖形的基本特征.因此，數學概念是對出現的數學現象通過數學思想進行分析、比較、歸納、推理等總結出來的規律.對稱圖形概念反映了數和形的本質，是本節課教學活動的出發點.

2 以數學思想為準繩，反映數學思維的科學本質

準確構建和掌握數學概念是學生探究和應用數學知識的前提，是學習數學理論以及證明、運算的基礎.大部分初中生對數學概念內涵的挖掘不夠重視，認為對數學概念的認知就是記住概念，在實際應用中并不能舉一反三.對于“中心對稱圖形”這個概念，記住了“圖形旋轉180°可以重合”，可以判定正方形、矩形、菱形或圓為中心對稱圖形，但對于對稱性的意義則不得而知.因此，記住了概念和知道其內涵是遠遠不夠的，還要弄清楚概念的外延.

在“對稱圖形”的復習課上，筆者通過一道經典的例題對“中心對稱圖形”的概念進行外延拓展.

典例如圖2，在矩形ABCD中，AB=3，AD=4，點P在AD上，PE⊥AC于點E，PF⊥BD于點F，則PE+PF=______.

圖2

筆者先作如下引導：

質疑3:矩形ABCD的對稱中心在哪里？

質疑4:兩條對角線將矩形ABCD分為4個小三角形，其中哪些小三角形是中心對稱圖形？

質疑5:兩條對角線將矩形ABCD分為4個小三角形，相對的小三角形面積一定相等.相鄰的小三角形面積是否相等？請給出說明.

預設目的：通過課堂引導，讓學生探究得出矩形的兩條對角線將矩形分為4個小三角形，這些小三角形面積一定相等.在證明過程中，讓學生進行交流，找出便捷的方法，開闊自己的視野.其預案如下.

方法2：折紙法.矩形是軸對稱圖形，將矩形沿對邊中心線依次對折，如圖3，得到一個小矩形，小矩形的對角線AO將其分為面積相等的兩個直角三角形，由此可以說明矩形的兩條對角線將矩形分為4個小三角形，這些小三角形面積一定相等……

圖3

學生通過不同的說明方法對“對稱圖形”的外延有了進一步的認知，接下來典例的解答就順理成章了.

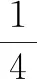
圖4

3 以數學建模為目的，彰顯數學素養的學科特征

在課堂教學實踐中，教師很容易走入經驗主義的迷途，因為所教的對象是八年級的學生，認為他們經過了一年多的初中學習生涯，對數學的認識達到了一定的水平，因此，對概念的生成、發展過程引導不到位.同時，在中考升學率和學生擇校的雙重壓力下，教師也容易簡單地將一些抽象、難理解的數學概念灌輸給學生，沒有為學生創設豐富詳細的質疑情境以幫助他們去理解，然后強迫學生下“題海”，導致結果常常事與愿違.因此，筆者變“題海”為“題舟”，將中考中的大題分解為小的質疑情境，“大題小做”.

在“對稱圖形”的復習課上，筆者以2021年江蘇省無錫市中考數學卷第17題作為課堂練習，對“對稱圖形”進行內涵和外延引導.

圖5

質疑6:對折出現的是軸對稱圖形，由此可知對稱軸兩側的對應線段相等.你得到了哪幾條線段相等？可以確定具體長度、角度嗎？

質疑7:請將圖形中的已知量與未知量標出來，觀察簡化后的圖形是什么樣的？

預案：如圖6所示.

圖6

質疑8:求AF需要數形結合，應該怎樣作輔助線？請寫出解題過程.

預案：

圖7

練習2關于中心對稱圖形類試題(略).

預設目的：練習1是對軸對稱圖形的鞏固，讓學生認識對折是軸對稱的應用；同時也使學生理解通過對稱圖形的對應關系可以找出對應相等的線段和角.另一方面，多次整合直角三角形中三邊“勾股定理”的關系，這是在沒有學習三角函數之前必須學會應用的定理.當然也有學生采用由直角三角形有一個公共角，知Rt△EFG∽Rt△EMF∽Rt△FMG，再利用相似比求出FM和EM的長度，但依然要用到“勾股定理”.

練習2在這里就不贅述了.

總之，筆者通過課堂零碎的環節預設，目的在于與初中一線教學的同仁進行深刻交流.由此得出，創設課堂質疑情境，要以數學概念為核心，折射數學理論的基本內涵；創設課堂質疑情景，要以數學思想為準繩，反映數學思維的科學本質；創設課堂質疑情境，要以數學建模為目的，彰顯數學素養的學科特征.只有這樣，才能使“質疑情境”有適宜性、發展性、內涵性，才能使學科素養的構建具備科學性、可行性、實用性.