基于2021年中考“方程與不等式”專題復習作業的設計*
?廣東省中山市東區遠洋學校初中部 麥雄軍
2021年各省市中考數學對方程與不等式的考查重點在于熟練掌握基礎知識和基本運算技能,側重于以當代實際生活為背景的問題解決,落實“以德樹人”的根本任務.2021年7月下旬,中辦、國辦印發的《關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見》(簡稱“雙減”政策),對作業提出了“發揮作業診斷、鞏固、學情分析等功能,將作業設計納入教研體系……”新的要求.這意味著教師要設計高質量且符合學情的作業,徹底減輕學生的負擔.筆者基于2021年各省市中考數學試題的研究,圍繞“方程與不等式”專題復習進行作業設計.
1 作業設計目標
通過作業,達成下列目標:
(1)復習和鞏固“方程與不等式”相關基礎知識,知道一元一次方程、二元一次方程組、一元二次方程、分式方程、一元一次不等式(組)的解法.
(2)領悟轉化、數形結合、數學模型、方程等數學思想,構建知識之間的聯系.
(3)學會解決相關綜合問題,提升分析問題、發現問題、解決問題的能力.
2 作業設計內容
2.1 夯實基礎,實施有效訓練
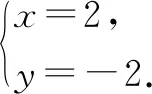
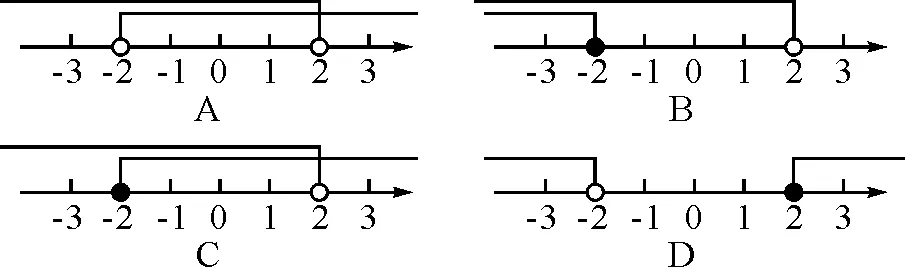
圖1
答案:C.
(3) (2021·吉林長春)關于x的一元二次方程x2-6x+m=0有兩個不相等的實數根,則m的值可能是( ).
A.8 B.9 C.10 D.11
答案:A.

答案:D.
設計意圖:作業(1)回顧了二元一次方程組的基本解法,可以采用代入消元法和加減消元法;作業(2)考查了一元一次不等式組的解法,借助數軸來理解不等式組的解集;作業(3)考查了一元二次方程根與判別式之間的關系;作業(4)考查了分式方程的解法.通過本環節的作業設計,這些基礎知識和基本技能將為下一階段的學習作好鋪墊.
2.2 積累經驗,活用思想方法

答案:3
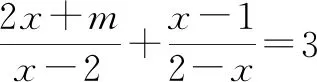
答案:m>-7且m≠-3.
(7) (2021·四川自貢)已知x2-3x-12=0,則代數式-3x2+9x+5的值是( ).
A.31 B. -31 C. 41 D.-41
答案:B
(8)(2021·湖北鄂州)數形結合是解決數學問題常用的思想方法.如圖2,直線y=2x-1與直線y=kx+b(k≠0)相交于點P(2,3).根據圖象可知,關于x的不等式2x-1>kx+b的解集是( ).

圖2
A.x<2 B.x<3 C.x>2 D.x>3
答案:C.
設計意圖:對于作業(5)中一元一次方程涉及的參數,只要抓住一元一次方程的概念,這道題便迎刃而解.作業(6)涉及分式方程的解法,把分式方程轉化為整式方程時,容易忽略分母不能為0;本題滲透了轉化的數學思想,以讓學生靈活掌握分式方程的解法.作業(7)滲透了整體的數學思想,通過轉化和整體代入解決數學問題.作業(8)滲透了數形結合的數學思想,通過圖形來直觀得到不等式的解集,抓住數學本質,積累解題經驗,達到“事半功倍”的效果.
2.3 注重綜合,發展數學能力
(9)(2021·湖南株洲)《九章算術》之“粟米篇”中記載了中國古代的“粟米之法”:“粟率五十,糲米三十……”(粟指帶殼的谷子,糲米指糙米),其意為:“50單位的粟,可換得30單位的糲米……”.問題:有3斗的粟(1斗=10升),若按照此“粟米之法”,則可以換得的糲米為( ).
A.1.8升 B.16升
C.18升 D.50升

故選:C.
設計意圖:本題旨在考查學生的閱卷理解能力,滲透數學史.本題難在用正確的數學語言表達數學問題,列出分式方程,并轉化單位.
(10)(2021·江蘇連云港)為了做好防疫工作,學校準備購進一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.
(ⅰ)這兩種消毒液的單價各是多少元?
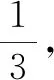
解析:(ⅰ)設A種消毒液的單價是x元,B型消毒液的單價是y元.

所以A型消毒液的單價是7元,B型消毒液的單價是9元.
(ⅱ)設購進A型消毒液a瓶,則購進B型(90-a)瓶,購買總費用為W元.

所以,當a=67時,最少費用為810-2×67=676元,此時,90-67=23.最省錢的購買方案是購進A種消毒液67瓶,購進B種23瓶.
設計意圖:本題是一道關于二元一次方程組、一元一次不等式、一次函數性質的綜合題,第(ⅰ)問也可以用一元一次方程來解答.旨在考查學生運用方程和不等式等數學知識解決生活中的實際問題,把實際問題轉化為數學問題的能力.在數學建模的過程中,提升學生發現問題、分析問題、解決問題的能力,并注重運算能力的培養,發展學生核心素養.
3 作業設計建議
3.1 作業設計應以核心素養為目標
在新時代背景下,數學教育的發展目標是提升學生數學素養.作業設計始終要以發展學生的核心素養為目標,不能盲目搞“題海戰術”,作業設計的練習不宜多,應給與學生充分思考的時間.設計的作業要讓學生經歷定理、概念的習得過程,注重學生數學抽象、邏輯推理等核心素養的培養;借助幾何直觀,滲透數形結合、轉化等數學思想,培養學生的直觀想象能力;注重學生運算能力、數學建模等核心素養的培養.總之,要把發展學生的核心素養落實到作業中.
3.2 作業設計應注重整體性
“雙減”政策要求“堅決克服機械、無效作業,杜絕重復性、懲罰性作業”,設計高質量作業的途徑之一就是從整體視角下開展教學.《義務教育數學課程標準(2011年版)》(以下簡稱《標準》)指出:“數學知識的教學,要注重知識的‘生長點’與‘延伸點’,把每堂課教學的知識置于整體知識的體系中,注重知識的結構和體系,處理好局部知識與整體知識的關系,引導學生感受數學的整體性.”[1]作業設計要從整體的角度出發,作業設計內容要體現整體性,基于《標準》和教材,以作業為載體,把數學知識之間的聯系有機融合,構建知識體系,提升學生數學思維,在問題解決中提升教育教學質量,實現高效作業.
3.3 作業設計應體現發展性
《標準》)指出:“教師教學應該以學生的認知發展水平和已有的經驗為基礎,面向全體學生,注重啟發式和因材施教.”[1]作業設計要體現層次性和發展性,從學生最近發展區出發,基于學生的知識經驗開展作業設計,避免出現偏題、怪題、難題,設計的內容由淺入深,環環相扣,由易到難,注重基礎知識和基本技能的掌握、數學思想的滲透、基本的數學活動經驗的積累,以“促進學生終身發展”為目標,落實“以德樹人”的根本任務.
3.4 作業設計內容應注重綜合性與情境性
《標準》)指出:“在注重對基礎知識和基本技能考查的同時,特別重視對具體情境中綜合運用知識分析和解決問題能力以及實踐能力的考查.”[1]作業設計內容要注重綜合性和情境性,讓學生體會數學來源于生活而又服務于生活.精選習題,精心設計情境性數學問題,讓學生在問題解決的過程中,體會數學的應用價值,提升學生的思維能力、實踐能力和解決實際生活問題的能力,發展學生的創新思維, 促進學生全面發展.

