循周期之律 探自學之道
——通過培養數學“小先生”提高學生自主學習能力*
冉春蓮
(西安交通大學蘇州附屬中學 215028)
《普通高中數學課程標準(2017年版)》指出,要提高學生從數學角度發現和提出問題的能力、分析和解決問題的能力(簡稱“四能”)[1].主動探究、自主學習有助于提高學生的“四能”.筆者在所帶班級實行陶行知先生倡導的“小先生”制:以波利亞解題法為指導,鼓勵一部分對數學感興趣(不一定是成績拔尖)的學生在老師和同學的幫助下收集素材,對學習資料進行挖掘和二次加工,以期在提高“小先生”個人水平的基礎上,創造良好的學習氛圍,培養學生在學習中注意前后聯系、凡事尋根究底的好習慣,在培養學生獨立探究能力的同時,提升學生的數學核心素養.下面以探索周期性為例介紹筆者的做法.
1 引例
在高一剛開始,筆者就給出波利亞的怎樣解題四步曲,鼓勵小先生們從是什么、為什么、怎么用等方面提高其研究數學問題的興趣,盡可能地對教學內容進行拓展、挖掘,并且注意積累總結出的結論和未解決的疑問.學生在集合部分對下面的問題(引例)進行了探索:
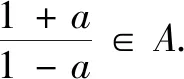
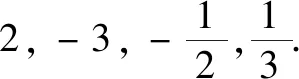
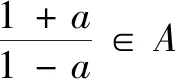
(3)還有其他的運算也具有周期性嗎?學生從“運算”出發,提出了相反數、倒數、負倒數都在周期性循環,并指出A中恰好是兩對負倒數——此時大多數學生還未學習周期性,但是聯系初中學過的循環小數,學生很自然地提出循環.新知識迅速融入已有的知識框架,學生感覺頗有收獲,體會到不能忽略任何一個知識點.
2 第一次聯系
例1已知函數f(x)對任意的x都滿足f(x)-2f(-x)=2x,則f(x)=.
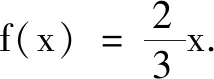
本題通過解方程組求函數解析式,其核心在于-(-x)=x,從函數觀點來看,就是函數f(x)經過若干次迭代之后可得到x,由此聯想到集合部分的引例,提出

改編題的思路非常清晰,但運算量超出學生的預料.大多數學生產生了畏難情緒.在教師的鼓勵下,小先生們身先士卒,攻克了運算難關,既提高了自身水平,也在班級樹立了威望.
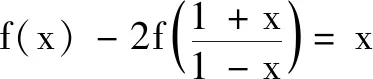
在解題反思時,學生發現解決這類題有規律性,包括運算過程可以用換元簡化,所謂“為之,則難者亦易矣”.通過建立與已有知識的聯系,不僅促進了學生數學運算素養的提升,也讓學生對抽象函數問題的解決有了更大的信心.
3 第二次聯系
例2對f(x)定義域內任一自變量的值x,若f(x+a)=-f(x)(a>0),則T=2a.
證明對f(x)定義域內任一自變量的值x,f(x+2a)=-f(x+a)=-(-f(x))=f(x),故T=2a.
通過例2,學生可以胸有成竹地給出下列結論:


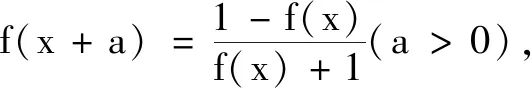
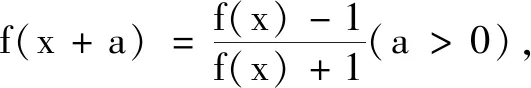
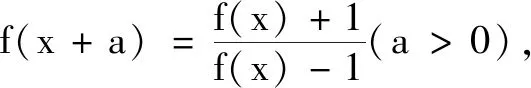
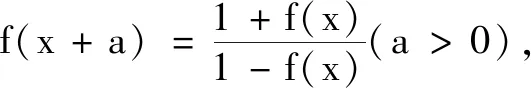
此時小先生團體已經不需要教師提醒而開始主動探索.他們聯系前面所學,總結歸納發現這一類問題的本質是周期,即函數迭代的周期性,他們提出了兩個問題:
第一,上述結論的證明過程都很相似,但這些高度近似“復制粘貼”的證明過程其實是個驗算性說明,為什么這樣形式的函數迭代之后有周期?
第二,為什么(3)(5)兩個類型的周期一致,并且周期都是(4)(6)的一半?
學生討論后的初步結果是:如果考慮函數f(x+a)=g(f(x)),(3)(5)中函數g(x)定義域和值域一致,而(4)(6)中函數g(x)定義域和值域不一致,且(3)(4)和(5)(6)剛好是互為相反數的關系.
事實果真如此嗎?作為教師,筆者并沒有直接指出原因,而是讓學生在這里作好標記,等待后續的學習并驗證.學生的歸納總結和追根究底都顯示出他們的數學抽象和邏輯推理素養已有提升,而他們未得到滿足的好奇心使得接下來的數學學習變得更加積極主動,更樂于探索知識之間的聯系以及數學公式的來龍去脈.
4 第三次聯系
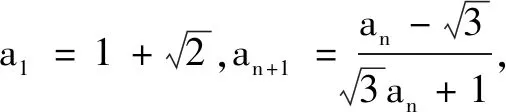
解析 {an}是周期數列,本題運算并不輕松,但其特殊的形式給了學生足夠的聯想空間——三角函數中有大量的周期性.

學生開始思考,如何將數列與三角結合解決有關周期性的問題,如:
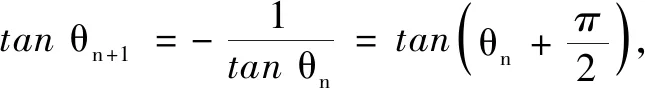

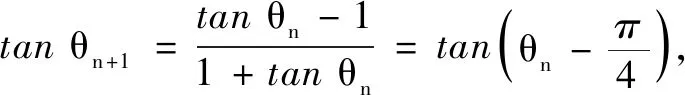
至此,學生長久以來懸而未決的疑問基本解決,并開始嘗試用這個方法盡可能多地探索周期性問題.引例在必修一剛開始提出,在選擇性必修二最終解決,問題解決的核心是周期性.初次出現于集合,在求函數解析式、函數周期的判斷、數列周期性均有應用,問題的證明則經歷了從數學運算進行驗證到結合三角函數知識進行證明的過程.在這個過程中,小先生制度漸漸在班級扎根,吸引了學生靠攏和加入,同時也取得了很多成果.
在上述過程中,學生不止獲得了基礎知識、基本技能,提升了類比推理、歸納推理等數學思想和核心素養,更重要的是有扎根于學生的數學活動經驗,讓知識、技能和思想方法有跡可循.
5 結束語
用本班的一位“小先生”的話總結本文:“我們對這個問題的研究的片段,很奇妙地和很多時候數學發展的過程非常相似:數學并不一定都是先證明后使用,反而可能是發現—猜想—證明—應用—再利用—找到根本原理,最后再建立理論體系.盡管某個結論不一定會一直記得,但其中互相關聯的任何一個環節都能讓我很快由此及彼確認結論,而這個思維過程每次回想起來都會令人感到愉悅,感到進步的快樂.”

