基于Kriging代理模型的中頻結構振動可靠性分析

方琛 秦朝紅 任方 張亞輝

(1 大連理工大學 工程力學系 工業(yè)裝備結構分析國家重點實驗室 大連 116024;2 北京強度環(huán)境研究所 可靠性與環(huán)境工程技術重點實驗室 北京 100076)

0 引言

工程結構在制造、運輸、裝配及服役過程不可避免地存在各種不確定性因素，所以在動態(tài)激勵作用下單純地計算結構的動力學響應或者響應的極值會忽視不確定性的影響。隨著計算能力和精細化建模需求的提升，結合概率論準確描述不確定性因素對動力學響應的影響，開展結構的動力學可靠度分析受到了廣泛關注。低頻問題在采用諸如有限元（Finite Element Method，F(xiàn)EM）等數(shù)值方法實現(xiàn)模型化后，通過概率模型結合抽樣或矩方法等即可得到結構的失效概率[1]。隨著頻率的升高，繼續(xù)采用FEM建模需要將網(wǎng)格劃分得足夠細，這會導致龐大的自由度數(shù)。在計算量難以負擔的同時，還會出現(xiàn)參數(shù)敏感性問題。當頻率足夠高時，充分考慮不確定性的集總參數(shù)的統(tǒng)計能量分析[2]（Statistical Energy Analysis，SEA）應運而生。可以通過響應的方差及近似概率分布描述非參數(shù)隨機的SEA模型的離散性[2-3]。

然而，實際工程結構在寬頻激勵下，不同組件的振動波長、模態(tài)密度等動力學特性差異較大，就會表現(xiàn)出中頻振動行為。傳統(tǒng)的低頻或高頻建模方法都無法直接應用。目前主要有兩種解決方案，一是傳統(tǒng)方法向中頻段的擴展[4-5]，二是基于子系統(tǒng)思想分別采用不同建模方法得到的中頻混合模型。其中Shorter和Langley基于擴散場互易關系[6]提出的混合有限元-統(tǒng)計能量分析方法（Hybrid Finite Element-Statistical Energy Analysis method，簡稱混合FE-SEA方法）[7]理論最為完善，在諸如航空航天等領域應用廣泛[8-9]。后續(xù)學者嘗試采用不同的方法替換FEM和SEA建立了不同的混合模型[10],[11]。為了實現(xiàn)中頻結構振動的可靠性分析，本文將采用混合FE-SEA方法實現(xiàn)模型化。

需要強調的是，混合FE-SEA方法將短波組件定義為統(tǒng)計性子系統(tǒng)，采用了集總參數(shù)的SEA建模，計算得到響應是已經(jīng)考慮了短波組件非參數(shù)不確定性的。而長波組件是完全確定性的，與實際不符。隨著現(xiàn)在計算能力的發(fā)展和對不確定性研究的需求，安全系數(shù)法已經(jīng)不能滿足現(xiàn)有結構的設計分析需求。Cicirello基于混合FE-SEA方法首次開展了中頻振動的結構可靠性分析[12]。Cicirello分別采用蒙特卡洛模擬（Monte-Carlo Simulation，MCS）和漸進近似拉普拉斯方法計算得到了彈簧-板組合系統(tǒng)的中頻結構可靠度。

混合FE-SEA方法的計算受制于復數(shù)總動剛度矩陣的求逆運算及譜分析形式，同等自由度規(guī)模下計算負擔遠大于FEM。那么對混合模型直接采用MCS求解可靠度的將進一步加劇計算負擔。此外基于混合FE-SEA方法建立的中頻問題的功能函數(shù)也格外復雜，采用傳統(tǒng)的可靠性分析方法求解比較困難。本文采用Kriging代理模型[13]-[15]直接建立隨機參數(shù)與響應的關系，從而避免復雜的原物理模型重分析。Kriging模型的精度依賴于樣本點的選取，對于混合方法建立的復雜的中頻振動求解模型，需要選取大量的樣本點，這樣會產生較大的計算量。為了在減少樣本數(shù)量的前提下保證計算精度，可以采用拉丁超立方試驗設計[16]（Latin Hypercube Sampling，LHS）得到布滿樣本空間的試驗組合，實現(xiàn)Kriging代理模型的全滿空間設計。故本文主要工作是基于混合FE-SEA方法的模型化，進一步考慮隨機參數(shù)構建了可靠性分析的功能函數(shù)，采用LHS結合Kriging模型構建代理模型實現(xiàn)中頻振動的結構可靠度分析。

1 中頻振動的混合FE-SEA模型

要實現(xiàn)中頻振動的結構可靠性分析，首先需要建立中頻振動的響應分析模型。本文采用經(jīng)典的混合FE-SEA方法實現(xiàn)中頻振動的模型化。混合FE-SEA方法將復雜系統(tǒng)的各個組件區(qū)分為長波變形子系統(tǒng)和短波變形子系統(tǒng)，然后分別采用FEM和SEA建模，最后通過擴散場互易關系實現(xiàn)系統(tǒng)響應的耦合求解。本節(jié)將對中頻結構的混合FE-SEA方法的基本理論進行介紹。

1.1 總運動方程

如圖1所示，混合FE-SEA方法將短波組件定義為統(tǒng)計性子系統(tǒng)，認為其是“直接場”與“混響場”的疊加。然后將混響場對直接場確定性邊界的作用定義為“混響場荷載”[6]。

圖1 混合FE-SEA模型的耦合示意圖 Fig. 1 Coupling of the hybrid FE-SEA method

為開展可靠性分析，本文進一步通過概率模型考慮長波組件的參數(shù)隨機特性，并將長波組件定義為隨機子系統(tǒng)。首先建立系統(tǒng)的總運動方程，其描述的是直接場效應和長波組件，寫作

其中()H表示共軛轉置，E[]表示集合平均，nj為第j個統(tǒng)計性子系統(tǒng)的模態(tài)密度，ω為激勵頻率。

為了聯(lián)立式(2)所示的擴散場互易關系，求總運動方程(1)建立的自由度q的互譜，表達式為

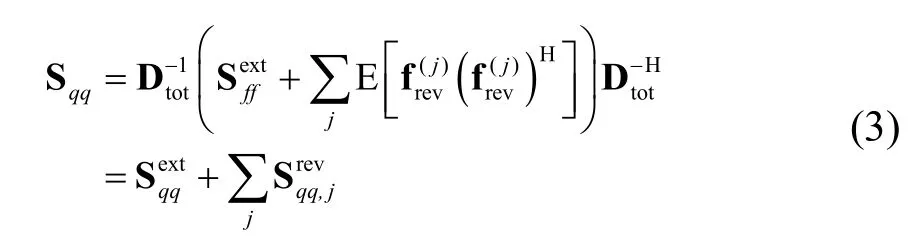
1.2 功率流平衡方程

根據(jù)功率流平衡關系，第j個統(tǒng)計性子系統(tǒng)的功率流平衡方程表示為[7]

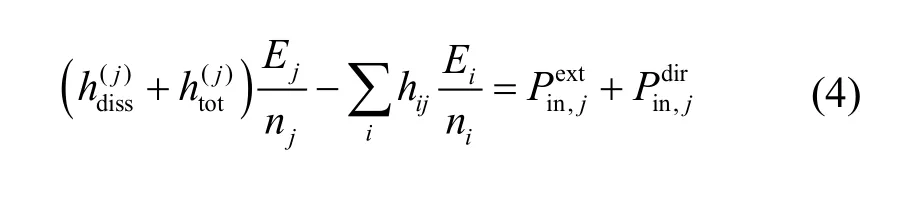
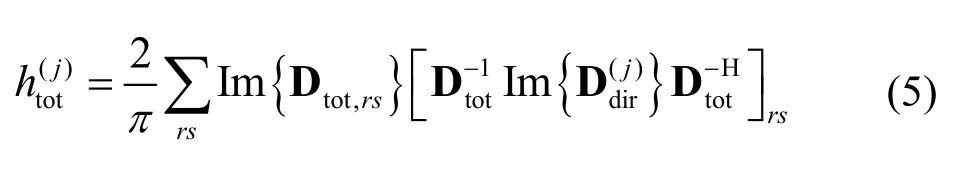
hij表示第j個統(tǒng)計性子系統(tǒng)混響場的單位模態(tài)密度輸入到第i個統(tǒng)計性子系統(tǒng)直接場的功率，表達式為

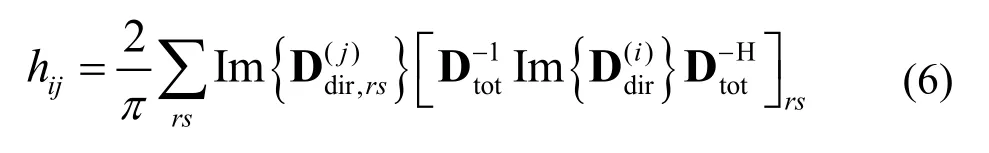
綜合式(5)～(7)，將m個統(tǒng)計性子系統(tǒng)的功率流平衡方程聯(lián)立為矩陣形式，表示為

E是由m個統(tǒng)計性子系統(tǒng)的能量組成的未知向量，是隨機子系統(tǒng)對各統(tǒng)計性子系統(tǒng)的輸入功率，N是各統(tǒng)計性子系統(tǒng)的模態(tài)密度組成的對角矩陣。L為系數(shù)矩陣，該系數(shù)矩陣的表達式為

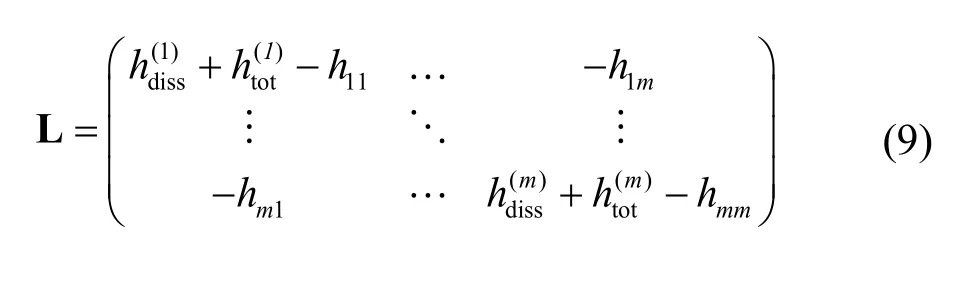
求解式(8)即可得到所有統(tǒng)計性子系統(tǒng)的能量，回代到式(3)即可求解得到的隨機子系統(tǒng)的響應Sqq。從系數(shù)矩陣L的表達式可以發(fā)現(xiàn)，混合模型求解需要首先計算總動剛度矩陣的逆，然后進行大量的求和運算，計算負擔很大。

2 中頻振動的結構可靠性分析

上一節(jié)通過混合FE-SEA方法實現(xiàn)了中頻振動的模型化，隨后即可開展結構可靠性分析。本節(jié)將建立可靠性分析的功能函數(shù)，并通過構造Kriging代理模型以避免復雜且計算量龐大的原物理模型的求解。

2.1 功能函數(shù)列式

基于混合FE-SEA方法進行結構中頻振動的模型化時，統(tǒng)計性子系統(tǒng)采用集總參數(shù)的SEA方法建模時充分考慮了非參數(shù)隨機性。在忽略了短波組件離散性基礎上，本文假設可靠性分析的n個隨機參數(shù)x=[x1,…xn]來源于定義為隨機子系統(tǒng)的長波組件的相關參數(shù)。將通過混合FE-SEA中頻隨機模型求解的響應表示為Q(x)。進一步可以將結構的極限狀態(tài)通過功能函數(shù)來表示

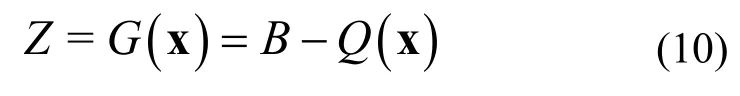
G(x)由結構的集合平均響應Q(x)和響應界限值B來決定。Z＞0、Z＜0和Z=0就表示結構處于安全、失效和極限狀態(tài)。通過采樣方法計算可靠度表達式為

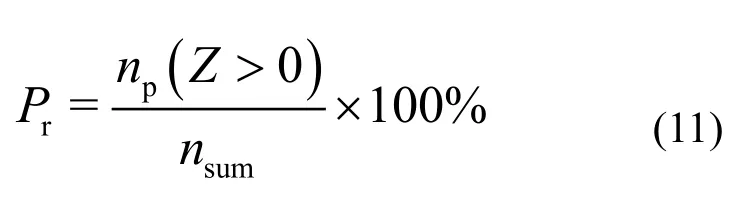
即可靠度為安全狀態(tài)的樣本數(shù)np(Z＞0)占總樣本數(shù)nsum的百分比。

2.2 Kriging代理模型

中頻問題的功能函數(shù)(10)由于響應Q(x)與隨機參數(shù)x=[x1,…xn]之間運算關系格外復雜，難以采用傳統(tǒng)的動力學可靠度方法求解。同時采用混合FE-SEA方法建立1.2節(jié)的功率流平衡方程時，必須直接對總動剛度進行求逆，然后進行一系列求和運算。如果隨機子系統(tǒng)的自由度規(guī)模較大，則計算負擔將難以承受。故采用Kriging方法建立等效響應求解的代理模型，結合滿樣本空間的LHS控制樣本點的選取，就可以建立式(10)所需的響應求解的等效方程。

Kriging代理模型是一個基于線性回歸分析建立的改進擬合模型。該模型包括回歸項和隨機項兩部分，對于一個函數(shù)y(x0)，其可以表示為

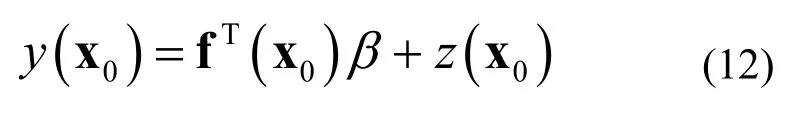
x0表示待測點；fT(x0)表示給定的多項式回歸模型；β表示待定的回歸系數(shù)；z(x0)表示隨機過程。z(x0)的均值為0，標準差為σz，協(xié)方差表示為

R(x1,x2)表示樣本點中任意兩點x1、x2之間與距離dj有關的變異函數(shù)。R(x1,x2)由核函數(shù)計算，有諸多相關方程[17]，廣泛使用的是高斯相關方程，寫作

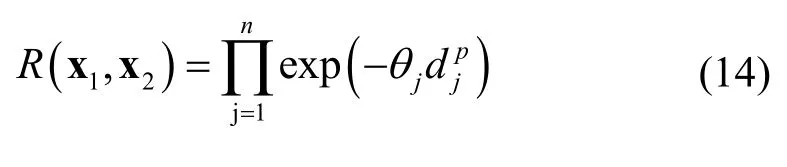
θj代表各向異性參數(shù)；p∈[0,2]表示光滑程度參數(shù)。

通過樣本數(shù)據(jù)X和對應響應Y，可以得到相關函數(shù)矩陣R。考慮待測點x0與N個樣本點X =[x1,…xN]的相關向量r (x0)，采用最大似然估計得到θj優(yōu)化值。進一步采用最小二乘法可得最大似然估計因子

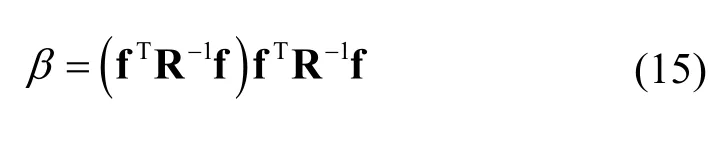
z(x)的方差估計表達式為

則Kriging代理模型在待測點x0處的預測值為

至此建立得到Kriging代理模型。

建立的Kriging代理模型的計算精度與效率依賴于樣本點的選取，為了有效的選擇充滿空間的少量樣本點，本文選擇比較主流的LHS[16]采樣方法。通過LHS建立滿空間的nk個樣本點，然后通過物理模型計算得到相應響應Q(x)。最后結合式(17)就可以建立Kriging代理模型，即一個近似的響應分析模型。

首先，建立代理模型所需的LHS樣本點要遠少于直接針對物理模型進行MCS的樣本點數(shù)。其次代理模型的計算效率要遠高于原物理模型，所以針對代理模型進行MCS即可迅速得到響應可靠度。本文采用成熟的DACE工具箱[18]建立Kriging模型，該工具箱簡便實用，被工程師和研究者們廣泛采用。

3 數(shù)值算例

本節(jié)將對如圖2所示的一個框架梁栓接板組合系統(tǒng)開展中頻結構動力學可靠度分析。該結構由一個邊長0.7m為正方體框架梁和四個長1.1m、寬0.6m的矩形板組成。梁截面為矩形，各板通過四個點栓接在框架梁上，各栓接點距離框架梁頂點0.1m。在原點o作用一個沿y軸正向的200Hz的單頻點荷載。框架梁的材料為鋼，阻尼損耗因子為0.01，板為鋁，阻尼損耗因子為0.02。

圖2 框架梁栓接板結構 Fig. 2 A framework-panel system

該模型其余材料屬性、幾何參數(shù)、荷載幅值等均為隨機參數(shù)，并考慮環(huán)境影響的不確定性。相關隨機參數(shù)的具體統(tǒng)計信息及概率分布見表1。

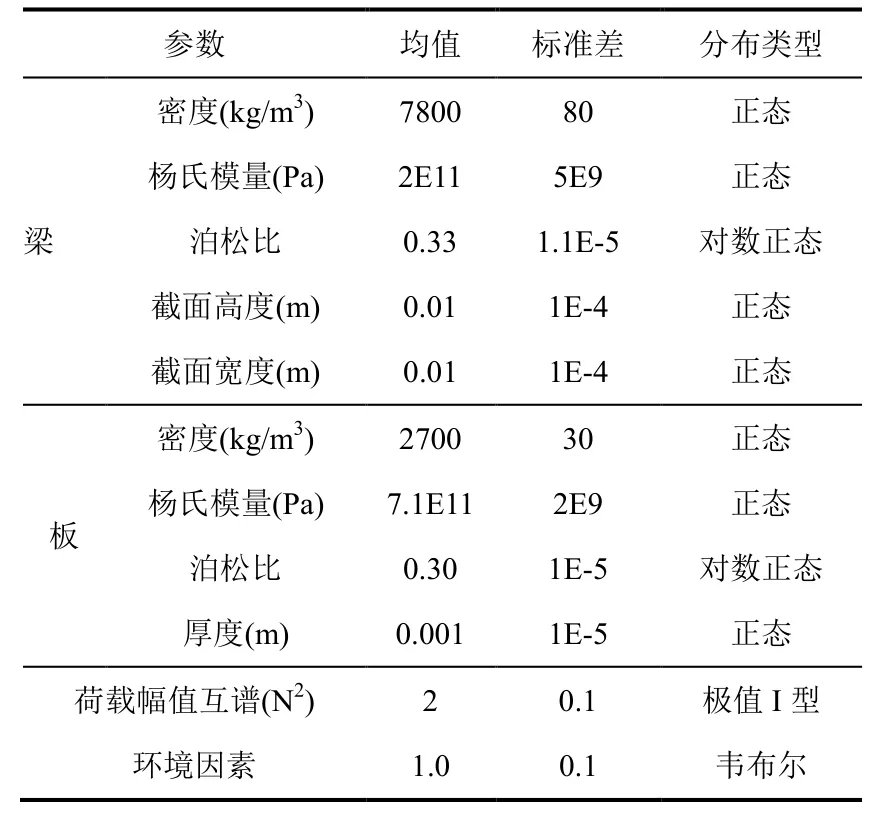
表1 隨機變量的概率分布參數(shù) Table 1 Probability distribution parameters of random variables

為開展可靠性分析，首先需要基于混合FE-SEA方法實現(xiàn)模型化。而混合模型的建模需要首先根據(jù)振動波長進行子系統(tǒng)劃分，200Hz激勵下梁和板的波長見表2，計算采用名義參數(shù)。如圖3 a)，將長波變形的梁和板面內振動定義為隨機子系統(tǒng)，采用FEM建模，網(wǎng)格尺寸為0.05m。如圖3 b)，采用SEA建模，將板短波變形的彎曲振動定義為統(tǒng)計性子系統(tǒng)。

表2 振動波長 Table 2 Vibrational wavelength

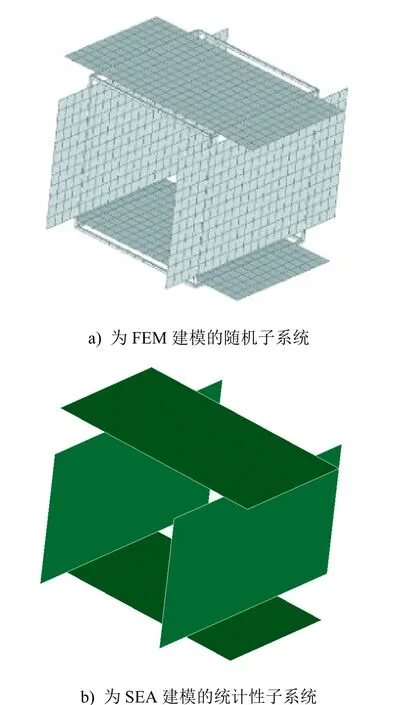
圖3 混合FE-SEA模型的劃分 Fig. 3 Subsystems of hybrid FE-SEA model

通過混合FE-SEA方法實現(xiàn)模型化后，即可開展可靠性分析。對于隨機子系統(tǒng)，選擇梁上的測點A(0.5, 0.7, 0.7)的速度幅值互譜Svv=1.66 ×10-5m2/s2為臨界變形。對于統(tǒng)計性子系統(tǒng)，選擇z=0.7m平面上的板的能量E4=5.42 ×10-4J 作為臨界能量。

對混合FE-SEA方法建立的原物理模型進行nm=105個樣本點的MCS[12]，將其計算結果作為可靠度參考解。對物理模型選取數(shù)量nk=500,600，1000的LHS樣本（隨機參數(shù)置信區(qū)間不小于99%）建立Kriging代理模型，可靠度計算結果如表3所示。通過nk=500個樣本點建立的代理模型計算的可靠度已經(jīng)接近MCS的結果，誤差均小于2%。隨著LHS樣本點的增多，誤差逐漸減小到低于0.5%。值得注意的是，該混合模型單次采樣計算都非常耗時，其中大部分時間耗費在總動剛度矩陣的求逆及相關的求和運算中。而采用代理模型計算近似響應的時間可以忽略不計。所以采用LHS采樣建立Kriging代理模型，求解可靠度的方法通過較小的計算量實現(xiàn)了中頻振動的結構可靠度求解。即使是LHS采樣數(shù)nk=1000，代理模型的計算時間只是nm=105次MCS的1%而已。而LHS采樣數(shù)為nk=500,600次時間，計算效率可以在MCS基礎上分別提升200、167倍。

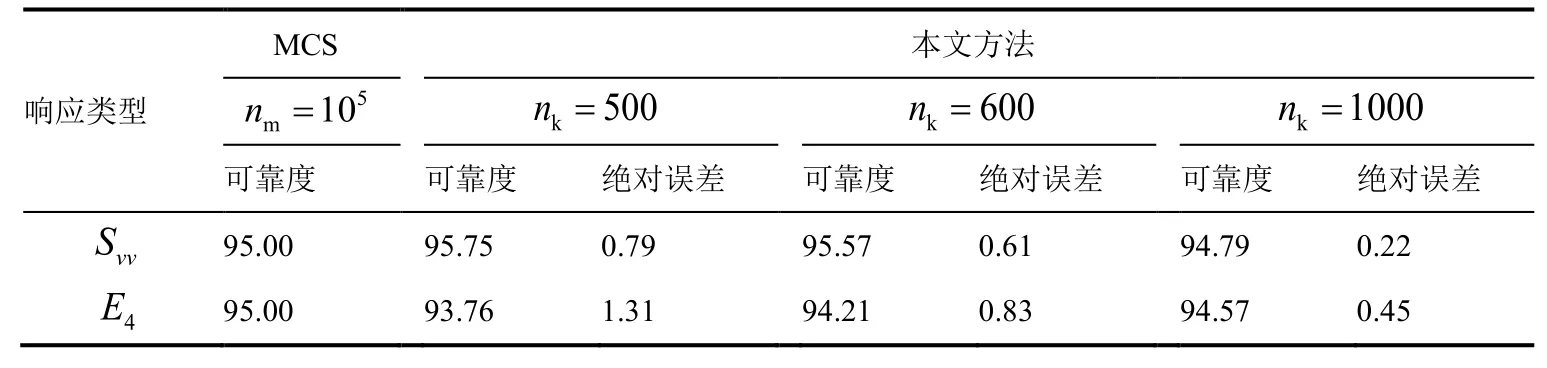
表3 結構可靠度分析結果(%) Table 3 Reliability analysis results (%)

進一步驗證更高可靠度下的結果。將測點A(0.5, 0.7, 0.7)的速度幅值互譜和z=0.7m平面上的板能量對應的臨界值重新給定為Svv=1.94 ×10-5m2/s2和E4=5.71 ×10-4J 。計算結果如表4所示，此時MCS得到的可靠度均為99%。采用nk= 1000個LHS樣本建立了Kriging代理模型，計算得到的可靠度誤差均小于1%。

表4 結構可靠度分析結果(%) Table 4 Reliability analysis results(%)

4 結論

本文開展了中頻振動的結構可靠性分析。混合FE-SEA方法將短波組件采用SEA建模，本文在忽略短波組件的離散性后通過概率模型描述長波變形組件的隨機性來開展可靠性分析。通過滿空間的LHS選取樣本點即可建立Kriging代理模型。針對一個框架梁栓接板組合結構計算可靠度。發(fā)現(xiàn)較之對物理模型通過大量采樣的直接MCS的方法，通過少量的LHS樣本點建立的代理模型可以迅速計算得到可靠度，計算效率很高。隨著LHS樣本點增多，誤差會逐漸減小。