空間幾何體中構(gòu)造輔助線的入手點
——以線線垂直問題為例

邵建鳳 李光彬

(山東省淄博市臨淄中學(xué))

空間幾何問題的解答有時需要構(gòu)造相應(yīng)的輔助線,輔助線是搭建已知與未知之間的橋梁,但在具體問題的求解中如何構(gòu)造輔助線呢? 本文以線線垂直問題為例,總結(jié)出了幾種構(gòu)造技巧,供讀者參考.

1 從最直接的關(guān)系入手

已知關(guān)系是題目條件所給的、可直接利用的,對已知關(guān)系的充分利用是構(gòu)造輔助線的首要入手點.

例1如圖1所示,在正方體ABCD-A1B1C1D1中,證明:A1D⊥BD1.

圖1

分析證明兩條異面直線垂直,常用的策略是構(gòu)造線面垂直,得到線線垂直,即把其中的一條線置于某一平面中,再證明另外一條線與該平面垂直.那么將哪條線置于平面中,如何構(gòu)造這一平面?

本題是將A1D置于某一平面中,還是將BD1置于某一平面中,可從已知中最直接的關(guān)系入手.

欲證兩條直線垂直,肯定會用到已知中的線線垂直關(guān)系,那么是否存在某條與A1D或BD1垂直的直線.不難發(fā)現(xiàn)A1D⊥AD1,這一垂直關(guān)系最為直接,因此先連接AD1,即可出現(xiàn)我們期待的結(jié)果.

證明如圖2所示,連接AD1,由于BD1?平面ABD1,故只需證明A1D⊥平面ABD1即可.由正方體的性質(zhì)易得A1D⊥AB,又A1D⊥AD1,AB∩AD1＝A,故A1D⊥平面ABD1,所以A1D⊥BD1.

圖2

2 從平面圖形的性質(zhì)入手

平面幾何圖形中的某些性質(zhì)是構(gòu)造輔助線的重要入手點,如等腰三角形、等邊三角形具有三線合一的性質(zhì),菱形對角線互相垂直平分,矩形對角線相等、互相平分等.這些性質(zhì)都是構(gòu)造輔助線的入手點.

例2如圖3 所示,已知三棱柱ABC-A1B1C1中,CA＝CB,AB＝AA1,∠BAA1＝. 證 明:AB⊥A1C.

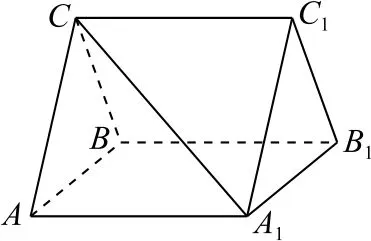
圖3

分析本題和例1一樣,也是證明兩條異面直線垂直,需要構(gòu)造線面垂直,那么是將AB置于某一平面中,還是將A1C置于某一平面中?

已知中給出CA＝CB,則△ABC為等腰三角形,具有三線合一的性質(zhì).又因為AB＝AA1,∠BAA1＝,所以△ABA1為等邊三角形,同樣具有三線合一的性質(zhì),因此可由此入手構(gòu)造輔助線.

證明如圖4 所示,取AB的中點D,連接CD,A1D,而A1C?平面A1CD,因此只需證明AB⊥平面A1CD即可.

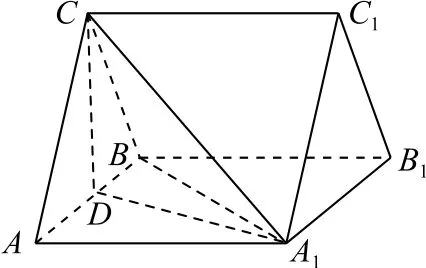
圖4

因為CA＝CB,所以AB⊥CD.因 為AB＝AA1,∠BAA1＝,所以△ABA1為等邊三角形,從而AB⊥A1D,且CD∩A1D＝D,故AB⊥平面A1CD,因此AB⊥A1C.

3 從滿足的結(jié)論入手

例3如圖5所示,在正方體ABCD-A1B1C1D1中,M為BC的中點,點N在四邊形CDD1C1及其內(nèi)部運動.若存在點N,滿足MN⊥A1C1,則點N的軌跡為( ).

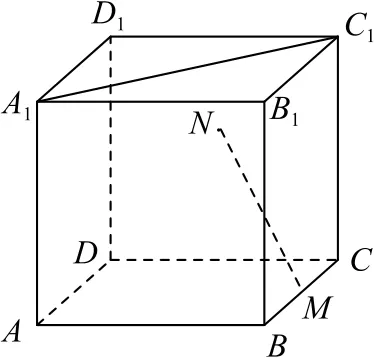
圖5

A.線段

B.圓的一部分

C.橢圓的一部分

D.雙曲線的一部分

分析本題中的點N滿足MN⊥A1C1,N是動點,MN是動線,A1C1是定線.動線與定線垂直,說明MN在一個與A1C1垂直的平面內(nèi)運動.因此通過添加輔助線,構(gòu)造出與A1C1垂直的平面,這是解決問題的關(guān)鍵.因為M是定點,因此可從點M入手構(gòu)造與A1C1垂直的直線.

解如圖6 所示,設(shè)P為棱CD的中點,連接PM.設(shè)Q為棱D1C1的中點,根據(jù)正方體的性質(zhì)知A1C1⊥PM,A1C1⊥PQ,且PM∩PQ＝P,所 以A1C1⊥平面MPQ,故點N∈平面MPQ.又點N∈平面CDD1C1,所以點N在平面MPQ與平面CDD1C1的交線PQ上,故點N的軌跡是線段,選A.

圖6

4 從基本模型入手

基本模型是指我們平時歸納總結(jié)的、存在垂直關(guān)系的一些常用模型.題目條件中如果存在基本模型的部分條件,我們可構(gòu)造相應(yīng)的輔助線,將其所隱藏的模型關(guān)系展現(xiàn)出來,從而利用模型解決問題.

例4如圖7 所示,正方體ABCD-A1B1C1D1的棱長為2,M為AA1的中點,P為側(cè)面ABB1A1的點,若D1P⊥CM,則PB的最小值為( ).

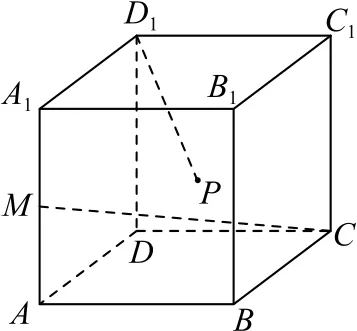
圖7

分析正方體的各個面均為正方形,在正方形中存在如下的基本模型.

如圖8 所示,在正方形ABCD中,M,N分別是BC,CD邊的中點,我們可以證明AM⊥BN.這一垂直關(guān)系在求解以正方體為背景的問題中經(jīng)常用到,如果題目已知條件中存在這種模型的部分條件,我們可添加相應(yīng)的輔助線構(gòu)造這一模型,并利用其解題.

本題以正方體為背景,在正方形ABB1A1中,M是AA1的中點,具備這一模型的局部條件,因此可進一步構(gòu)造模型.

解如圖9所示,令A(yù)B的中點為N,連接BM,B1N,B1D1,D1N.利用圖8 中的基本模型可得B1N⊥BM.

圖8

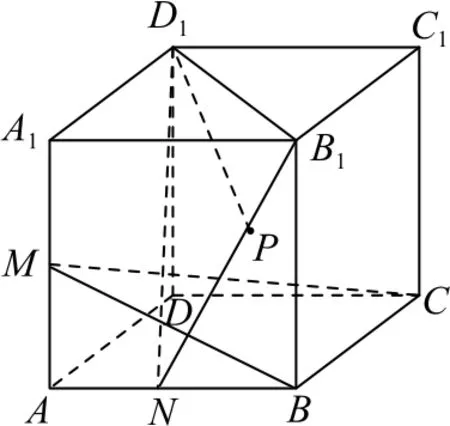
圖9

由正方體的性質(zhì)可知B1N⊥BC,且BM∩BC＝B,所以B1N⊥平面MBC,所以B1N⊥CM.又因為D1B1⊥平 面A1ACC1,CM?平面A1ACC1,所以D1B1⊥CM,且D1B1∩B1N＝B1,故CM⊥平面D1B1N,而D1P?平面D1B1N,所以點P在線段B1N上.

通過上面的分析可知PB的最小值也就是點B到線段B1N的垂直距離,利用平面幾何知識可求得PB的最小值為,故選C.

綜上所述,在空間幾何問題的求解中,準(zhǔn)確構(gòu)造輔助線是關(guān)鍵,只要我們在平時的學(xué)習(xí)中注意積累、總結(jié)輔助線的構(gòu)造技巧,結(jié)合具體題目條件準(zhǔn)確構(gòu)造相應(yīng)的輔助線,問題即可迎刃而解.

(完)