GLOBAL SOLUTIONS TO A 3D AXISYMMETRIC COMPRESSIBLE NAVIER-STOKES SYSTEMWITH DENSITY-DEPENDENT VISCOSITY*

Mei WANG (王梅)

School of Sciences，Xi 'an University of Technology，Xi'an 710048，China E-mail : wangmei0439@163.com

Zilai LI (李自來)

School of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo 454000，China E-mail: lizilai0917@163.com Zhenhua GUO(郭真華)

School of Mathematics and Information Science,Guangxi University，Nanning 530004，China E-mail : zhenhua.guo.math@gmail.com

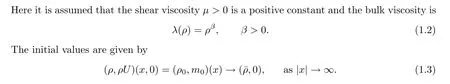
The compressible Navier-Stokes equations have been studied by many authors. There has been significant progress on the well-posedness theories of the compressible Navier-Stokes equations (1.1) when both the shear viscosity and the bulk viscosity are positive constants.It is well-known that the global well-posedness theory for the one-dimensional case is rather satisfactory; see [2, 3] and references therein. For the multi-dimensional case, the local wellposedness theory of classical solutions was established in the absence of a vacuum (see [4, 5]),and the global well-posedness theory of classical solutions was obtained for initial data close to a non-vacuum steady state (see [6]). The short time well-posedness of either strong or classical solutions containing a vacuum was studied recently by Cho-Kim [7] in the 3D case, where a natural compatibility condition on the initial values is imposed when the vacuum states do occur. Later, [8] generalized Cho-Kim’s [7] result to the 2D case. One of the fundamental questions is whether these local (in time) solutions can be extended globally in time. The first pioneering work along these lines was the well-known theory of Matsumura-Nishida [6], and after that there appeared some satisfactory results about the global well-posedness theory with small initial data close to a non-vacuum steady state(see[9]and references therein). Meanwhile,the global well-posedness of classical solutions to the 3D isentropic compressible Navier-Stokes equations with small energy was proved by Huang-Li-Xin [10]. The global existence of weak solutions with large initial data permitting vacuums was proposed in [11-13]. The analysis allowed for the initial data to be arbitrarily large with the vacuums, so the solution would also have vacuums and the global well-posedness could not be expected; see [14-16] for the blow-up results of classical solutions.

The case in which both the shear and bulk viscosities depend on the density has also received a lot of attention. However,few results are avaiable for the multi-dimensional problems,and even the short time well-posedness of classical solutions in the presence of a vacuum remains open. The first successful example is attributed to Guo-Jiu-Xin in [17], with spherically symmetric initial data and fixed boundary conditions. Later Guo-Li-Xin extended this to the free boundary conditions with discontinuously symmetric initial data [18]. Chen and Zhang in[19] showed a local existing result with spherically symmetric initial data between a solid core and a free boundary connected to a surrounding vacuum state.

Meanwhile, some progress on the global well-posedness theory of (1.1) with large data and a vacuum has been achieved since Vaigant-Kazhikhov[1] proposed the system (1.1)-(1.2).Vaigant-Kazhikhov [1] established the global well-posedness of the classical solution to (1.1)under the condition β >3 and that the initial values are uniformly away from vacuum states.Then the global existence and large time behavior of weak solutions was studied by Perepelitsa in [20] in the special case that β = γ >3. For when initial values contain vacuum states, Jiu-Wang-Xin[21] first proved the global well-posedness of the classical solution to the 2D periodic problem with large data provided that β > 3 and some compatibility conditons are satisfied.Then Huang-Li improved the index β to be β >43in [22]. For the 2D Cauchy problems with vacuum states at far fields, Jiu-Wang-Xin [23] and Huang-Li [24] independently considered the global well-posedness of a classical solution in quite different weighted spaces. It is worth pointing out that the solution established in the two-dimensional decomposition method in[1] is no longer applicable in three dimensions. For the cases of general density-dependent viscosity coefficient λ(ρ), Ye [25] had got the global well-posedness of classical solution to Cauchy problem of three-dimensionl. Recently, for the “fluid region” of the whole space or with a free boundary, which was introduced by Hoffin [26], the authors of this paper obtained that the global existence of the weak solution to 3D spherically symmetric compressible and isentropic Navier-Stokes equations with arbitrarily large initial data when the shear viscosityμis a positive constant and the bulk viscosity is λ(ρ) = ρβ, while 0 ≤β ≤γ, γ is the adiabatic exponent in the γ-law pressure function ([27, 28]).

The notation (···)+denotes the positive part of (···), and the same letter C (sometimes used as C(X) to emphasize the dependence of C on X) will denote various positive constants.

2 Main Result

For axisymmetric flow,there is no flow in the θ-direction and all θ derivatives are identically zero. Thus we consider only two variables: r, which is the radial direction, and z, the axial direction. We denote the fluid density and the fluid velocity by ρ and u=(u1,u2), respectively,while u1and u2are the radial and axial components of the velocity,respectively. More precisely,we are mainly concerned with the following axisymmetric solution to the problem (1.1):

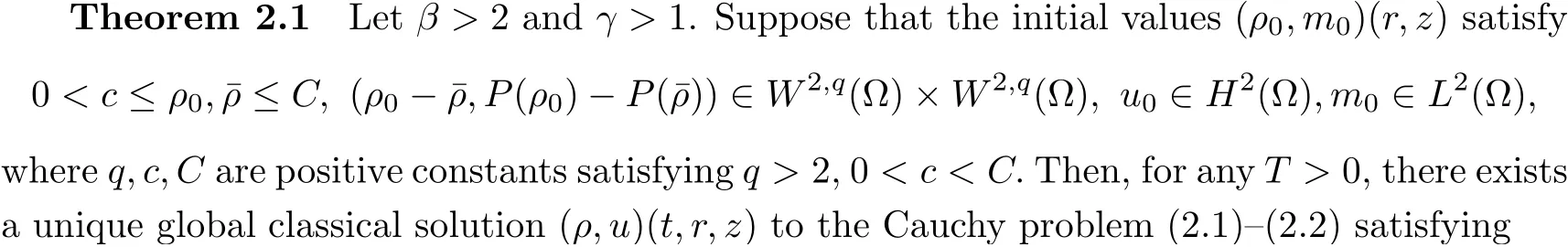
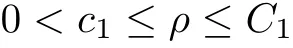
for some positive constants c1and C1.

The rest of the paper is organized as follows: in Section 3 we will present some elementary facts that can be used later. In Section 4 we get a priori estimates which will be needed to obtain the global solution. The sketch of the proof of main result is given at the end of Section 4.

3 Preliminaries

In a fashion similar to[1], we introduce some variables and denote the effective viscous flux as follows:

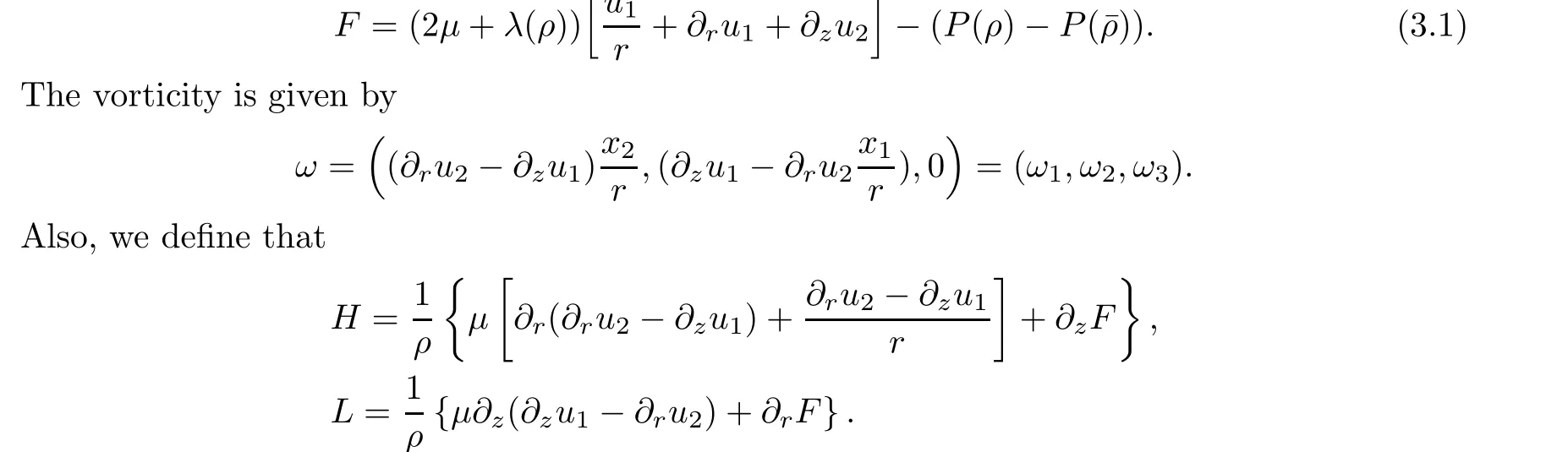
with the positive constant C independent of m, and where Amis the optimal constant.

4 A Priori Estimates

In this section, we will prove some a priori estimates and then obtain the upper and lower bounds of the density.

Step 1 Elementary energy estimates:

Lemma 4.1 There exists a positive constant C depending on (ρ0,m0) such that

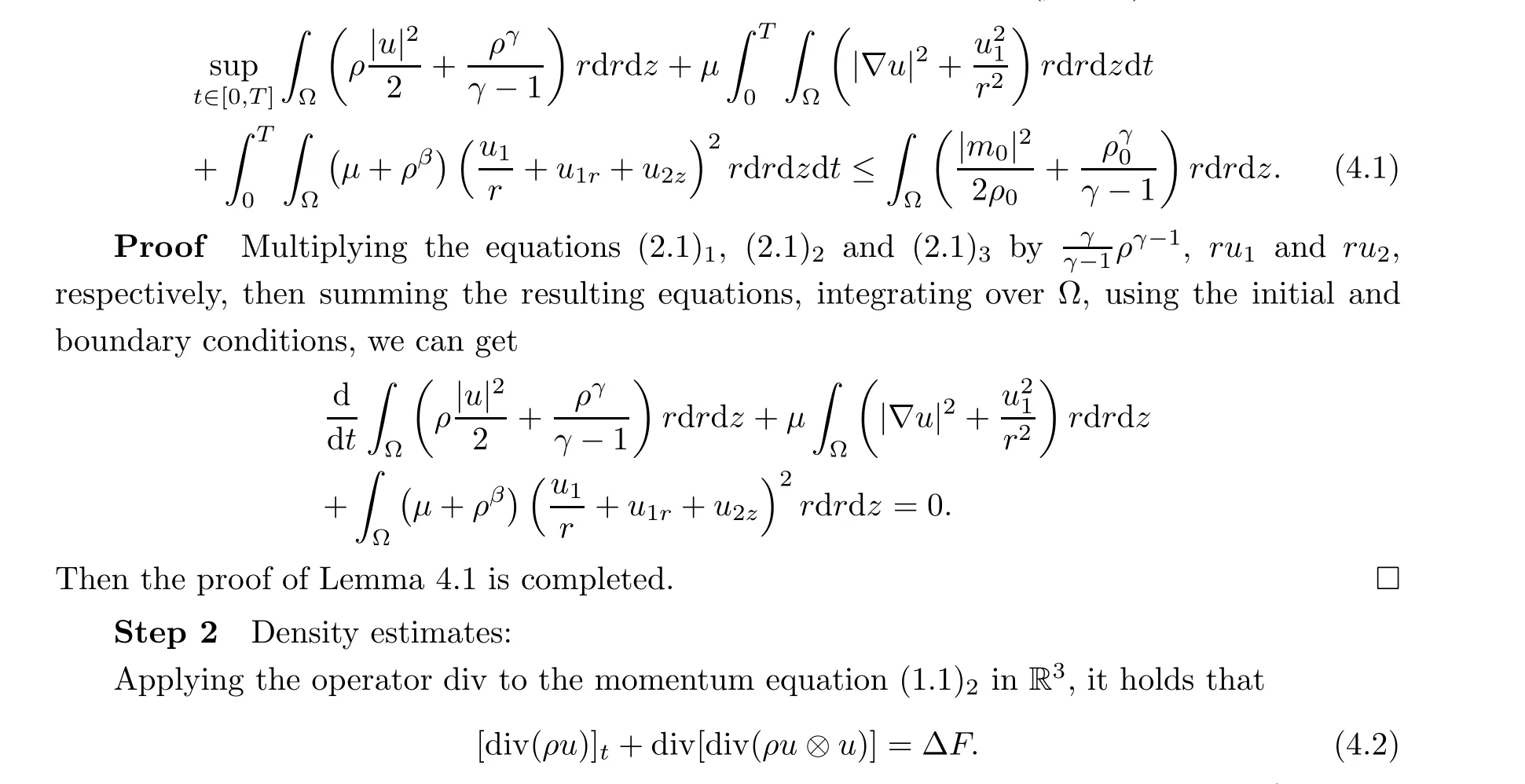
Defining

we can obtain a new transport equation as follows in Ω0:

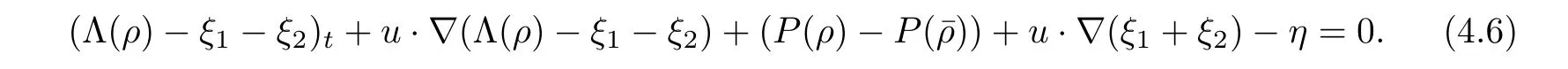
This is also the same form in the axisymmetric case where ?:=(?r,?z)in Ω,and,for simplicity,we regard equation (4.6) as the axisymmetric form in Ω. Meanwhile, we state the following estimates for a later calculation: by the elliptic estimates and H¨older inequality, we have

Lemma 4.2 For any k >1 and m ≥1, we have the following estimates in the domain Ω:

We can obtain the density’s Lpestimate by the above useful lemmas.

This completes the proof of Lemma 4.5. □

Now one can obtain the upper and lower bounds of the density by using the transport equation (4.6).

Lemma 4.6 There exist positive constants C1and C2such that

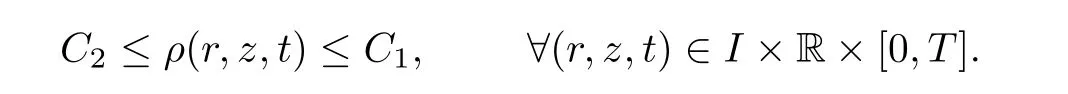
Remark We know that because the weight function r is a periodic function, i.e., r ∈I ?(0,+∞), all of the above lemmas that we have proved in Ω are also valid in Ω0. Thus, we only need to prove the fact that c1≤ρ(x,t)≤c2, in Ω0×[0,T]. In Lemma 4.6, all the norms ‖·‖prepresent the norm ‖·‖Lpin Ω0.

Proof By the definition of ξi(i = 1,2) from (4.3) and (4.4), u · ?(ξ1+ ξ2) - η =[u,RiRj](ρu), where [·,·] is the usual commutator, and Ri,Rjare the Riesz operators. Thus,from (4.6), it holds that

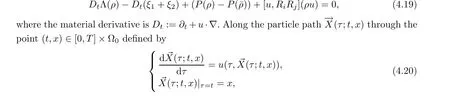
from equation (4.19), we have the ODE

The proof of Lemma 4.6 is completed. □

5 Proof of Main Result

Finally, we will give a sketch of the proof of our main result.

Proof of Theorem 2.1Under the assumptions of Theorem 2.1, the local existence of the classical solution can be proven in a way similar to that in [8]; we omit it for simplicity. In view of the lower and upper bound of the density,we can get the higher order a priori estimates and one can extend the local solution to the global one by using these a priori estimates in a standard way. The proof of Theorem 2.1 is completed. □