方程組有解問題轉化為方程有解問題的思考*

俞杏明

(江蘇省興化中學 225700)

數學問題解決過程中，經常需要把方程組有解問題，轉化為方程有解問題，這必須考慮轉化是否等價.

1 解答質疑引發思考

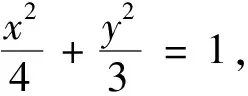
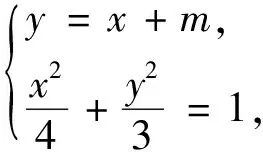
2 溯源而上挖掘隱含

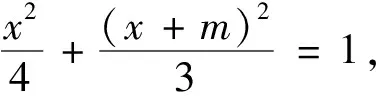
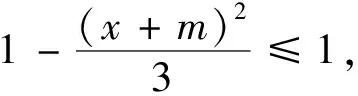
所以方程7x2+8mx+4(m2-3)=0若有解，則解一定在[-2,2]內.

3 提煉升華生成結論

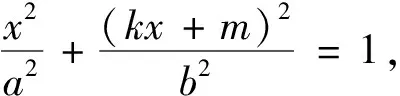
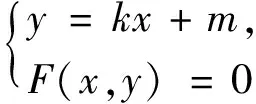
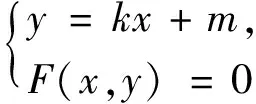
同理有：

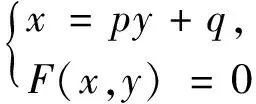
例2若2x2-2xy+y2=1，求x+2y的最小值與最大值.

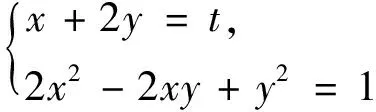
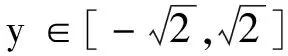
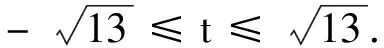
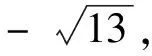
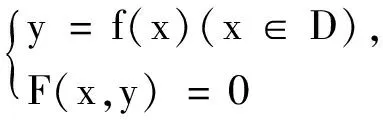
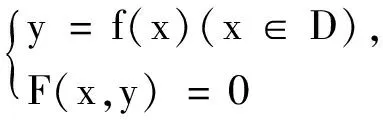
類似地，

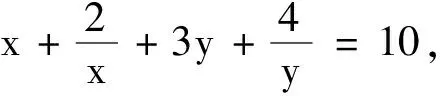
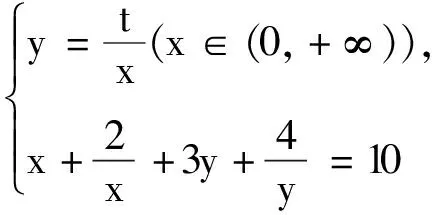
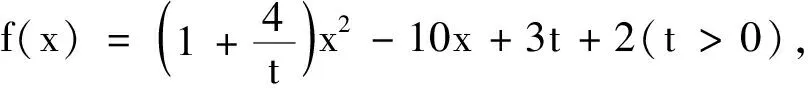
4 隱含對應一一兼顧

方程組有解問題轉化為方程有解問題時，有時會出現意想不到的錯誤.

例4若曲線C1：y2=2x與曲線C2：(x-m)2+y2=2有交點，求m的取值范圍.

這個答案顯然是錯誤的，當m取較小負數時，兩曲線處于相離狀態，沒有交點.那么，錯誤的根源是什么？如何避免這樣的錯誤？下面先從簡單事例入手進行探討.

“互聯網+健身參與”是在“互聯網+”時代背景下，應用現代化、智能化、信息化等科技創新為全民健身參與服務。例如“智能夜跑”、“悅動跑團”等健身跑模式，屬于利用“APP軟件+互聯網”技術監控體育活動運動量、消耗量、睡眠質量及其他身體健康指標等功能的智能化形式，而通過在朋友圈的“曬跑”、“曬健身”等行為大大激發了全民健身參與的興趣，各種約跑、約教練、約運動活動層出不窮，促進了運動“趣緣”群體的形成，也方便群眾省時、省力地進行體育運動。

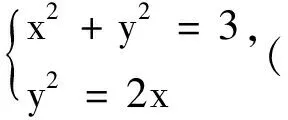
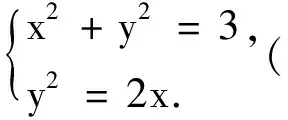
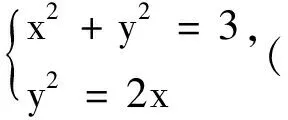
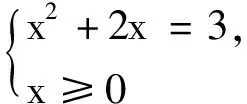
對剛才的例子進行一般化，有如下結論：

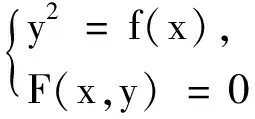
同理有：

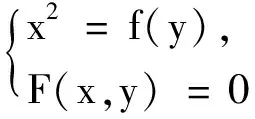
更一般地，有以下結論：

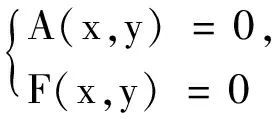
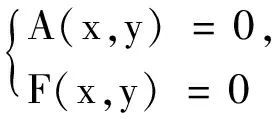
下面我們重新求解例4.

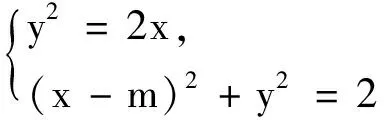
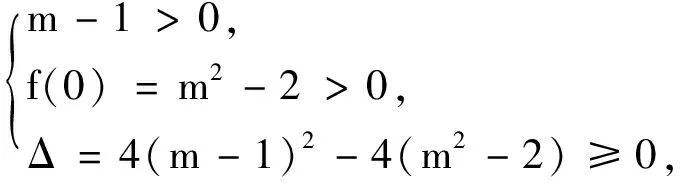
把例4改編為下面兩道例題，體現推導出的結論的效力.

例5若曲線C1：y2=2x與曲線C2：(x-m)2+y2=2有四個交點，求m的取值范圍.

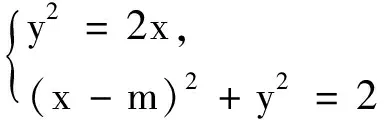
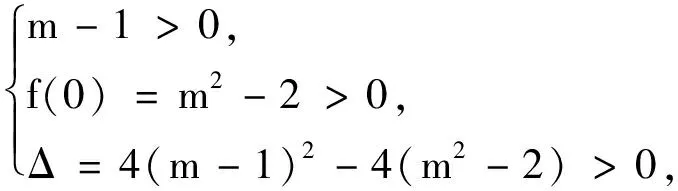
例6已知曲線C1：y2+4y=2x與曲線C2：(x-m)2+y2+4y=2有且僅有兩個公共點，求m的取值范圍.

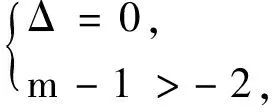
5 一點說明

代入消元法是處理方程組最基本、最常用的辦法.有些方程組盡管需要特殊技巧整理，但最終仍回歸到代入消元法軌道上.至于更多元(二元以上)的方程組，可以在文中理念下等價轉化為二元方程組，進而用文中結論求解.