LLC平面變壓器繞組損耗與漏感改進有限元計算方法

趙志剛 張學增

LLC平面變壓器繞組損耗與漏感改進有限元計算方法

趙志剛1,2張學增1,2

（1. 省部共建電工裝備可靠性與智能化國家重點實驗室（河北工業大學） 天津 300401 2. 河北工業大學河北省電磁場與電器可靠性重點實驗室 天津 300401）

有限元法常被用于平面變壓器繞組損耗、漏感等參數的精準計算。然而，受到計算與存儲成本的限制，在設計周期較為緊張的條件下，可精確計算的設計方案數量有限，增加了將局部最優點選為最終設計方案的風險。為縮減有限元法的計算與存儲成本，該文針對有限元法資源占用較大的線性方程組構建與求解這一過程進行改進。首先，通過分析平面變壓器磁場強度分布規律，依據邊緣效應影響強弱，將求解區域劃分為強邊緣效應區域與弱邊緣效應區域；其次，引入更為契合弱邊緣效應區域的一維線性單元，從而減少描述求解域場量的節點數與單元數，進而減少線性方程組系數矩陣階數，達到節約計算與存儲資源的目的；再次，通過調節相鄰單元節點分布規律，解決由于引入一維線性單元而產生的單元兼容、系數矩陣構建等問題；最后，搭建平面變壓器模型，通過對比繞組損耗、漏感的實驗值與計算值以及對比該文方法與有限元法計算、存儲成本，驗證了該文方法的有效性。

平面變壓器 有限元法 繞組損耗 漏感 數值計算

0 引言

隨著電動汽車、互聯網通信、新能源發電等領域的快速發展，具有結構簡單、零電壓軟開關（Zero Voltage Switch, ZVS）以及零電流軟開關（Zero Current Switch, ZCS）寬頻率范圍、電磁干擾較弱以及隔絕偏磁電流等優點[1-4]的LLC串聯諧振變換器（下文簡稱LLC變換器）被廣泛應用于直流配電系統、電動汽車充電裝置、服務器電源適配器等電能轉換設備中[5-12]。LLC變換器中“LLC”的含義為此變換器拓撲中影響電壓增益的諧振電感r、勵磁電感m與諧振電容r。

高頻變壓器作為LLC變換器重要組成部分之一，其繞組損耗、漏感等參數對LLC變換器的工作效率、功率密度、散熱、電壓波動等性能具有不可忽視的影響。平面變壓器作為高頻變壓器的一種，相比于傳統繞線式變壓器，具有高度更低、散熱性能較強、產品一致性較好、更易于集成等優點，被廣泛應用于LLC變換器中[13-16]。

由此可見，平面變壓器繞組損耗、漏感等參數的建模和計算方法對LLC變換器的設計制造具有一定程度的指導意義，因此也受到國內外LLC變換器設計者以及相關研究人員的廣泛關注。

在工程實際中，LLC變換器所用平面變壓器模塊的常見設計策略為：①通過快速計算方法對大量變壓器設計方案進行初步參數計算；②依據初步參數計算結果篩選出較少數量的備選設計方案，不可否認的是，這些備選方案中包含了一定數量的局部最優設計點；③通過精確計算方法對備選設計方案進行更為精準的性能參數計算，從而選定所設計磁性器件的最終設計方案[17]。

在最終設計方案選擇階段，精確計算方法的計算及存儲成本決定了在固定設計周期內，其能夠計算備選設計方案的數量。可精確計算備選方案的數量越少，將局部最優設計點選為最終設計方案的風險將越大。

顯而易見的是，通過縮減精確計算方法的計算與存儲成本，增加在一定設計周期內精確計算的備選方案數，是誤選局部最優設計點為最終設計方案問題的有效解決方案。現有平面變壓器繞組損耗與漏感精確計算方法可分為統計法與數值法。

統計法中，文獻[18]通過對大量繞組損耗與漏感數據進行響應面分析，得到繞組損耗、漏感與變壓器結構參數間的二次回歸關系。而文獻[19]則是通過大量的有限元仿真計算值訓練出變壓器結構參數與繞組損耗、漏感間的人工神經網絡。雖然以上兩種方法的計算與存儲成本較少，但需要預先提供足量的計算或實驗數據集，用以支撐二次回歸和人工神經網絡的準確性。然而工程實際中，在無法提前確定備選方案具體結構的情況下，很難預先獲取支撐統計法的數據集，從而使得統計法在設計平面變壓器過程中受到了一定程度的限制。

數值法中，文獻[20]首先通過鏡像法將平面變壓器磁心窗口磁場擴展為無限大周期平面，再借助二維傅里葉級數求解出繞組導體截面邊界磁場，最后計算出平面變壓器繞組損耗與漏感。文獻[21-22]通過3D有限元法對平面變壓器磁場強度分布進行了仿真，3D有限元法對平面變壓器的仿真更符合其實際運行情況。然而較為高昂的儲存以及計算成本（GB數量級的存儲量占用，十幾分鐘甚至小時數量級計算時間），使得3D有限元法一般無法被應用于平面變壓器設計過程中。文獻[23-24]借助2D有限元法計算出平面變壓器繞組損耗與漏感等參數，可勝任平面變壓器性能參數計算的準確度以及較低的計算與存儲成本，使得2D有限元法常用于平面變壓器繞組損耗與漏感的精確計算。

本文方法主要針對2D有限元法計算與存儲成本的縮減問題進行改進，以最終達到在平面變壓器設計過程中減少選取局部最優點為最終設計方案風險的目標。

需要補充的是，在2D有限元計算過程中，代數方程組的構建與求解過程往往占據了較大的計算與存儲資源[25]。因此，如何有效地減少代數方程組構建與求解過程的計算與存儲成本成為縮減2D有限元法計算與存儲成本所面臨的重要問題。

為有效地縮減線性方程組構建與求解階段的計算與存儲成本，本文首先分析了平面變壓器磁場強度分布規律，根據邊緣效應對磁場強度分布影響的強弱程度，將平面變壓器劃分為強邊緣效應區域與弱邊緣效應區域；其次，在區域劃分的基礎上本文方法引入一維線性單元，并將其應用于與其更為契合的弱邊緣效應區域；再次，通過限制相鄰一維線性單元與三角形單元節點重合，解決了由于引入一維線性單元所造成的單元兼容、系數矩陣構建等問題，在幾乎不影響繞組損耗、漏感計算精度的同時，有效縮減了代數方程組構建與求解過程的計算與存儲資源；最后，通過對比平面變壓器模型繞組損耗、漏感的實驗值與計算值，驗證了本文方法的有效性。

1 磁心窗口建模分析

本文方法是在磁準靜態場假設條件下對渦流場有限元法的改進，其本質仍為電磁場邊值問題，邊值問題由泛定方程與邊界條件組成。與此同時，本文方法是針對平面變壓器繞組損耗計算與漏感計算這一應用背景的改進，因此本節將主要討論針對平面變壓器電磁場求解問題時，泛定方程的構建過程與邊界條件處理過程。

1.1 磁準靜態場假設

磁準靜態場假設即忽略位移電流密度d對整個求解域場量分布的影響，可以簡化有限元法泛定方程的離散剖分過程以及后續貢獻方程構建，常被用于平面變壓器繞組損耗與漏感計算流程中。

然而，忽略位移電流密度d將影響全電流密度的大小，同時還使得整個求解域電磁場的波動性也被忽略即全電流密度作為激勵源與所引起的響應磁場強度是即時依賴關系。由此可見，磁準靜態假設的適用性判定條件為位移電流密度d遠小于傳導電流密度c，且求解域空間尺寸V遠小于時變電磁場所產生電磁波的波長，即

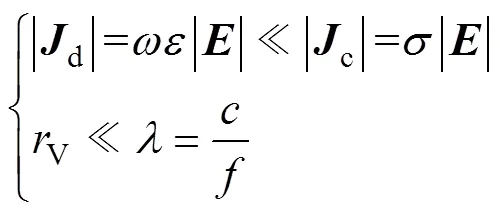
式中，為角頻率，=2p，為工作頻率；為材料介電常數；為材料電導率；為光速；為電場強度。

受到開關器件死區時間d、磁心相對磁導率r有效范圍、繞組材料趨膚深度以及功率損耗loss等因素影響，平面變壓器工作頻率一般選定在100kHz～1MHz這一數量級范圍內。在這一工作頻率范圍內，在10-5這一數量級，而銅的電導率在107這一數量級，能夠滿足位移電流密度d遠小于傳導電流密度c這一判定條件。另一方面，即便是在1MHz工作頻率條件下，時變電磁場電磁波波長仍可以達到300m，遠超平面變壓器1～30cm的空間尺寸V。由此可見，在通過有限元法計算平面變壓器繞組損耗與漏感時，可將求解域內的電磁場視為磁準靜態場。

1.2 泛定方程構建

LLC諧振變換器拓撲結構如圖1所示，為使整流二極管VD1、VD2工作在ZCS狀態的同時盡可能減小反向恢復效應，系統工作頻率一般設定在r1這一諧振頻率附近，其具體計算方法為

此時流過平面變壓器導體截面的諧振電流r波形接近于正弦波。因此電流源激勵下的時諧渦流場求解器可以較為真實地描述LLC變換器中平面變壓器及其周圍磁場。因此，可選用磁準靜態場以矢量磁位為變量的雙旋度方程作為平面變壓器場量求解所需的泛定方程。

然而，受到渦旋電流密度e的影響，無法預先確定求解域內導體截面源電流密度s，需要額外補充電流密度在導體截面上的積分等于導體截面電流這一約束條件。

泛定方程具體形式為

1.3 邊界條件處理

泛定方程構建完畢后，需要給定求解域邊界條件以構成電磁場問題的精確數學描述并使得泛定方程具備定解條件。在100kHz～1MHz這一工作頻率范圍內，平面變壓器所使用的鐵氧體磁心等效相對磁導率r在1 000～2 000甚至更高。

圖2所示為磁心窗口與磁心分界面，以相對磁導率為2 000的3F3鐵氧體磁心為例，由磁感應強度折射定律可知，當空氣側磁通密度1的入射角1=1°時，磁心側磁通密度2的折射角2已經達到88.3°。由此可見，對于平面變壓器磁心，可將磁心近似看作理想導磁介質即交界面附近窗口空氣側磁通密度1垂直進入交界面（1=0°），依據矢量磁位與磁通密度的關系可知，在交界面磁心窗口一側，的法向偏導數為0，如式（4）所示。在設置邊界條件時，磁心窗口與磁心交界面上設置諾依曼邊界條件即可滿足泛定方程定解條件。

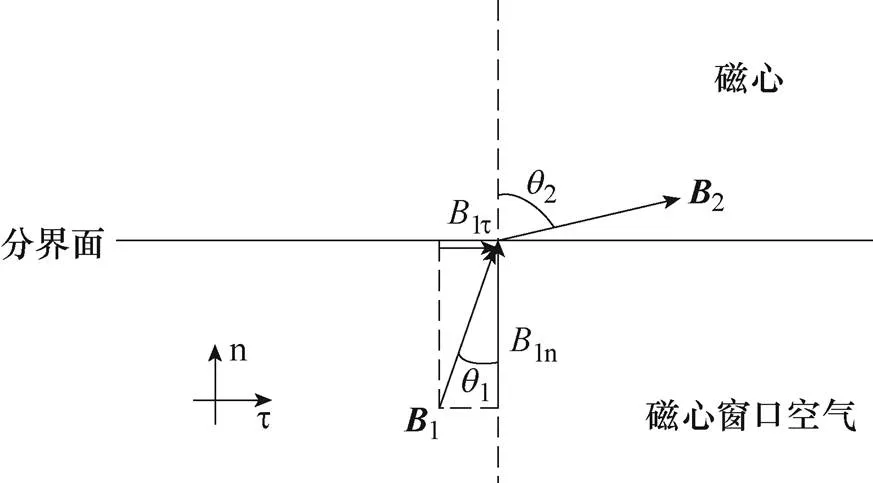
圖2 磁心與磁心窗口分界面

式中，t為交面切向單位矢量；n為交界面單位法向矢量；1t為磁通密度在交界面磁心窗口一側的切向分量；1n為磁通密度在交界面磁心窗口一側的法向分量。

通過以上方法處理后，平面變壓器的求解區域由整個變壓器壓縮到磁心窗口區域，并且如式（4）所示諾依曼邊界條件在有限元法線性方程組構建過程中自然滿足，無需特殊處理，可有效節約有限元法在計算平面變壓器繞組損耗與漏感時的計算成本。

2 改進有限元計算方法

2.1 區域劃分

以200kHz工作頻率平面變壓器磁心窗口磁場強度橫向分量H分布為例，磁心窗口橫向磁場強度H分布云圖如圖3所示，圖3中，點畫線框內磁場橫向分量H幾乎沿橫向不變，僅沿縱向變化，較為符合磁場強度一維分布假設，然而剩余區域受到邊緣效應影響，磁場強度橫向分量H在橫向上仍然有變化，不符合磁場強度一維分布假設。

圖3 磁心窗口橫向磁場強度Hx分布云圖

依據磁場強度分布規律的差異，本文方法將磁心窗口區域劃分為強邊緣效應區域ed與弱邊緣效應區域weak，磁心窗口區域劃分如圖4所示。通過針對不同區域實施不同的剖分策略，可有效降低描述求解域所必須的節點數與單元數，從而達到縮減有限元法計算與占用存儲資源的目的，在有限的設計周期內降低了選擇局部最優點為最終設計方案風險的目的。

圖4 磁心窗口區域劃分

本文方法對有限元法的主要改進部分在于，在弱邊緣效應區域使用一維線性單元剖分，而不是傳統的三角形單元，弱邊緣效應區域場量符合磁場強度一維分布假設，此區域磁場強度沿橫向不變這一特性決定了此區域可通過少量節點場量表示，從而達到降低有限元線性方程求解過程存在占用并降低此過程計算時間的目的。本節將主要針對討論弱邊緣相應區域的單元剖分問題、一維線性單元與傳統三角形單元的兼容性問題、線性方程組系數矩陣構建等問題進行討論。

2.2 單元剖分

由第2.1節可知，分布于弱邊緣效應區域磁場強度較為符合磁場強度一維分布假設，磁場強度在同一橫坐標下幾乎相等且僅沿縱向變化，2D有限元法中矢量磁位僅有軸分量A，通過式（5）對比可知，矢量磁位在弱邊緣效應區具有同一橫坐標下相等且僅沿縱向變化的特征，即

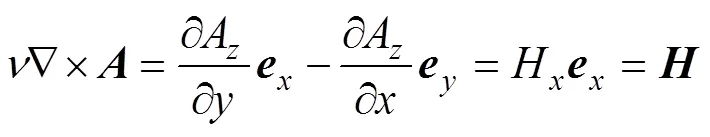
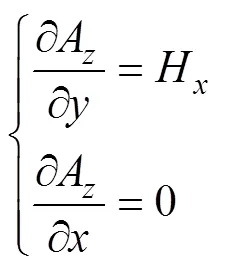
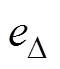
圖5 單元結構

為用剖分離散形式更為精確地表示求解域，并解決三角形單元與一維線性單元的兼容性問題，在本文方法前處理階段，三角形單元與一維線性單元需要遵守如下剖分規則。

（1）任意一維線性單元的節點不能是三角形單元邊上的點，任意三角形單元的節點不能是一維線性單元邊上的點。

（2）受鄰近效應影響，單元剖分尺寸不能僅以趨膚深度為依據。根據經驗，選擇1/4及以下銅箔厚度作為剖分尺寸的初值，具有良好的計算精度。

（3）邊緣效應主要受到縱向磁場強度H的影響，受鄰近效應影響較弱，因此應在導體邊緣處開始選擇3倍及以上最低頻率對應趨膚深度max作為強邊緣效應區域至弱邊緣效應區域的分界面，即圖4中ed應滿足ed≥3max，本文中ed=1mm。

（4）為方便后續線性方程組總體合成階段貢獻方程的參數計算，應使得節點縱坐標y與y滿足y＞y。

與此同時，在本文方法的前處理階段，可將弱邊緣效應區域壓縮，僅繪制強邊緣效應區域，網格剖分簡化處理如圖6所示，從而簡化有限元法前處理過程。

圖6 網格剖分簡化處理

2.3 單元分析

一維線性單元，以單元為例，單元組成如圖圖5b所示，通過線性插值可由、兩節點場量描述單元內部節點場量值。

為描述一維線性單元內部常量，首先需要得到僅與單元形狀有關的基函數，其表達式為

矢量磁位可通過基函數近似表示為

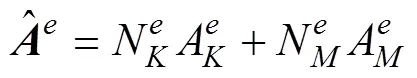
依據伽遼金法將式（7）、式（8）代入式（3）可得到任一單元（以單元為例）對有限元線性方程組的貢獻方程即

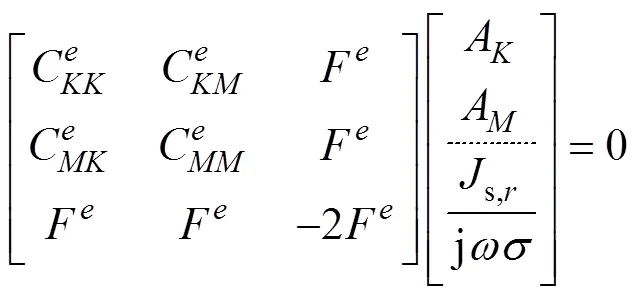
其中

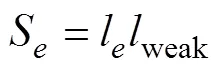
式中，s,r為導體截面中的源電流密度。

為方便后續對線性方程組的總體合成，將式（9）的系數矩陣改寫為貢獻矩陣的形式，即

式中，為單元所在導體層數；p為節點總數。

通過式（13）的改寫，將貢獻矩陣相加即可得到有限元線性方程組所對應的系數矩陣為

系數矩陣確定后即可得到本文改進有限元法待求線性方程組為

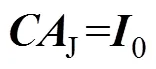
為能夠更為清晰地了解式（15）具體結構，特此列出其更為詳細的方程組形式為

式中，C為矢量磁位貢獻矩陣元素；為節點矢量磁位；F、F為源電流密度貢獻矩陣元素；s,k為導體截面中的源電流密度，2D有限元法中此物理量退化為標量；c,k為截面面積；I為通過導體截面的電流大小；r為導體截面總數。

將矢量磁位求解完畢后即可通過有限元后處理過程得到平面變壓器單位長度繞組損耗Cuel、漏磁能量mel。

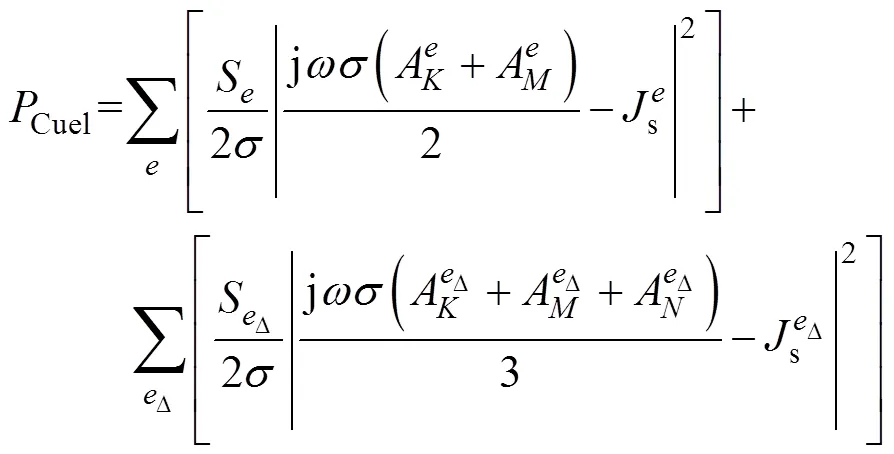
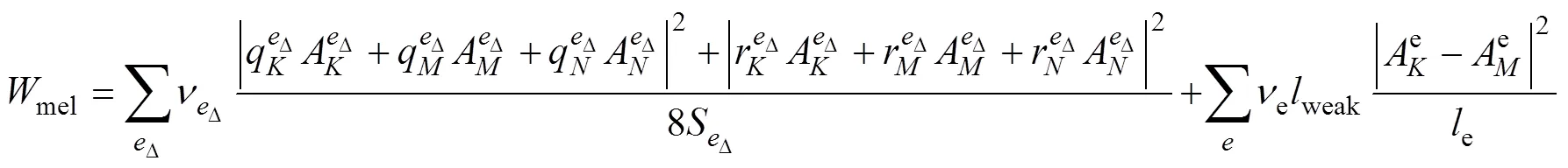
3 實驗驗證

3.1 實驗模型結構

為驗證本文方法的有效性，搭建了一臺12層平面變壓器模型與一臺4層平面變壓器模型，二者基本尺寸如圖7、圖8所示。

平面變壓器模型所用磁心材料為3F3，3F3這一材料的相對磁導率在工作頻率超過1MHz時會發生較為明顯的畸變，磁心截面平均磁場強度與磁通密度間會產生較為明顯的相位差，對后續實驗測量產生無法忽視的影響，因此本文選擇1MHz作為實驗測量的頻率上限。

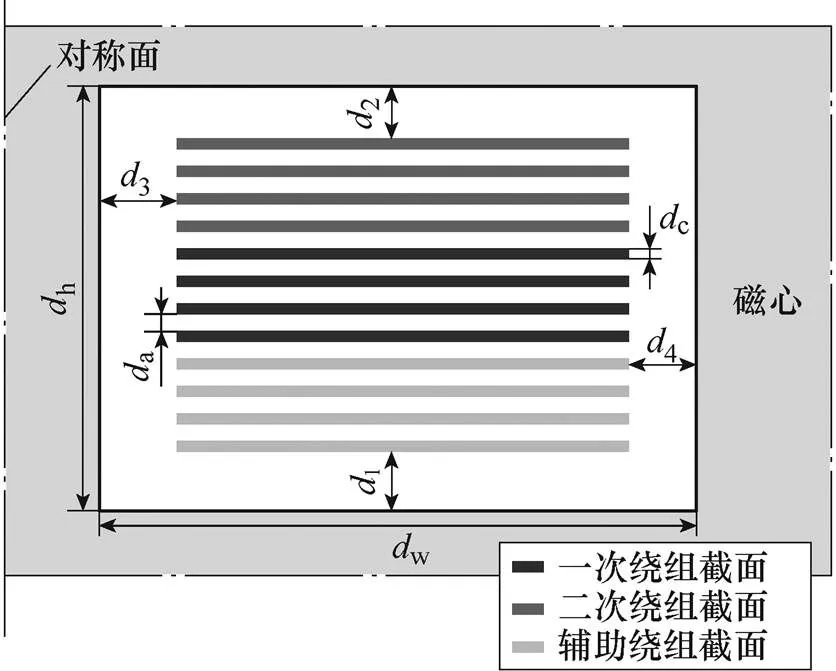
圖7 平面變壓器12層模型尺寸含義

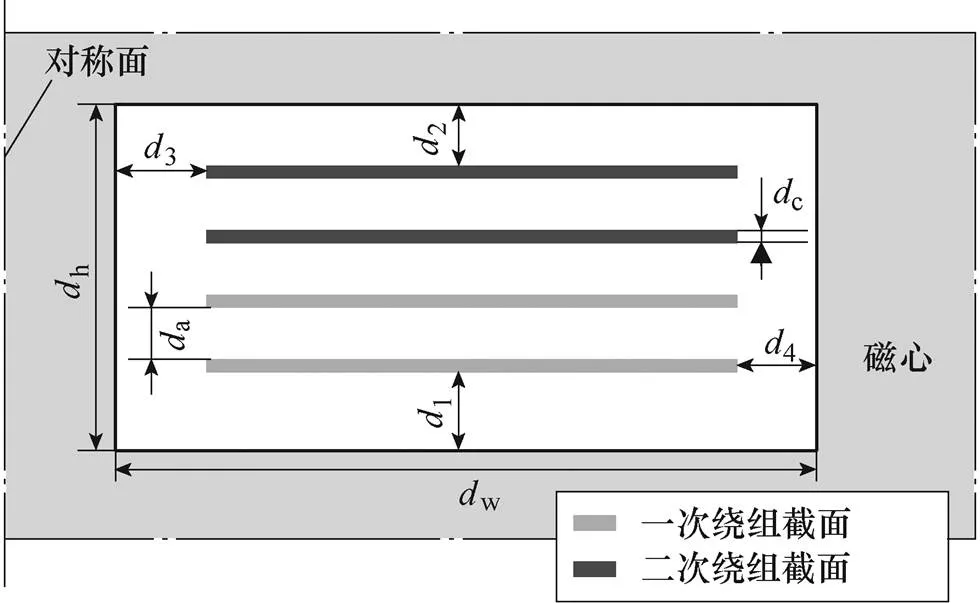
圖8 平面變壓器4層模型尺寸含義

本文方法對2D有限元法的改進集中于削減其計算成本與存儲成本，而計算精度則依賴2D有限元法的計算精度。綜合考慮2D有限元法計算精度與頻率限制，平面變壓器12層模型的實驗測量頻率將選定為200～400kHz，平面變壓器4層模型的實驗測量頻率將選定為100kHz～1MHz。

平面變壓器12層模型與4層模型的尺寸、材料以及結構的具體參數見表1、表2。

表1 平面變壓器模型尺寸

Tab.1 Sizes of planar transformer （單位: mm）

表2 平面變壓器結構以及材料參數

Tab.2 Structure parameter and material parameter of planar transformer

為方便對比分析，需要進一步計算得到一次、二次繞組損耗之和，漏感之和的計算值ssc、Cusc分別為

本文方法對2D有限元方法改進的目標：在幾乎不改變有限元法對平面變壓器繞組損耗、漏感計算精度的同時縮減2D有限元法的計算與存儲資源。因此，本節將通過兩方面驗證本文方法的有效性；一方面于3.2節對比本文方法與2D有限元法的計算、存儲資源占用；另一方面于3.3節對比本文方法與2D有限元法的計算精度差異。

3.2 計算存儲資源占用對比

本文方法與經典2D有限元法在計算規模與計算成本上的對比見表3。需要補充說明的是：

（1）計算時間所統計的是，平面變壓器12層驗證模型在200～400kHz范圍6個頻率工作點下以及平面變壓器4層驗證模型在200kHz～1MHz范圍內9個頻率工作點下，線性方程組構建、存儲與求解的總時間。所采用的線性方程組求解方法為雙共軛梯度（Biconjugate Gradient, BICG）法。

（2）本文方法與有限元法的計算目標約束為余量方程J=0在迭代過程中的相對殘差d＜1×10-6（10-4%），相對殘差d計算公式為

表3 計算規模及成本對比

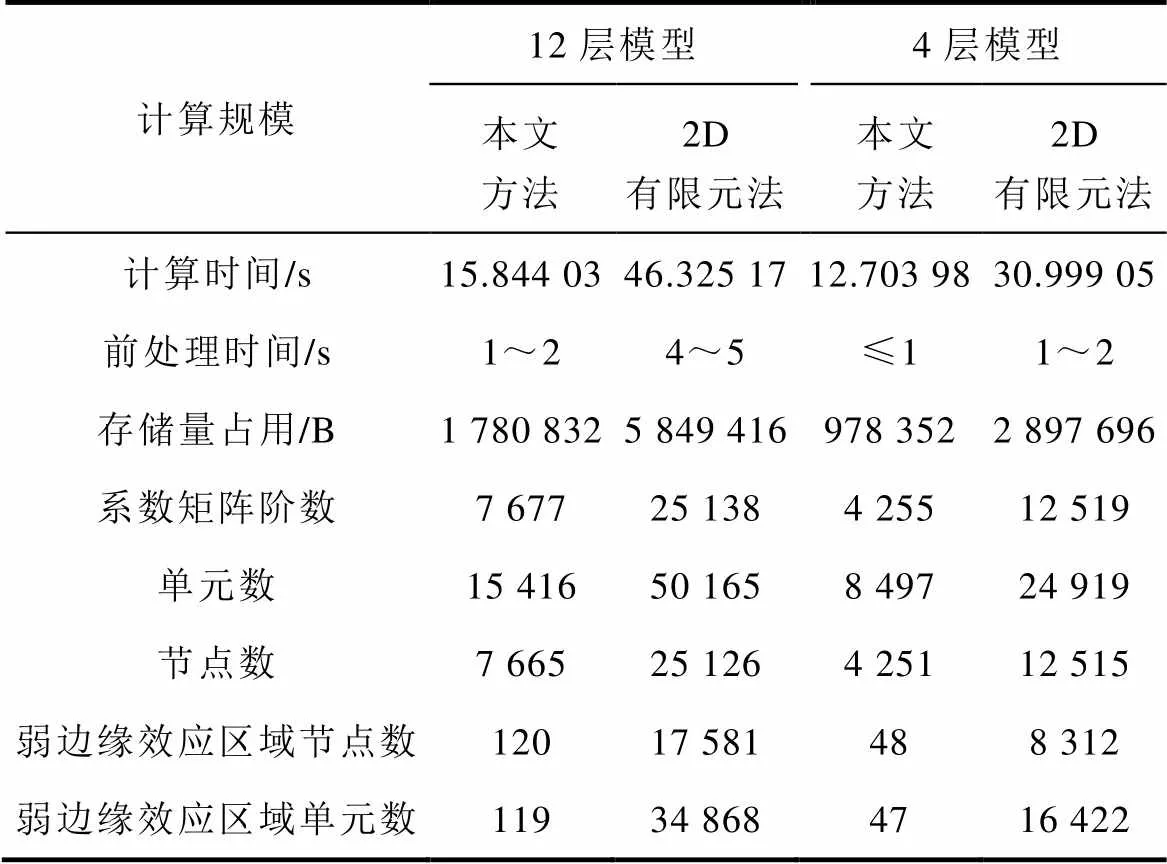
Tab.3 Scale and cost of calculating

式中,“|| ||”代表列向量的模，各矩陣、列向量的具體結構如式（15）、式（16）所示。

（3）表3中節點數、單元數是通過磁場能量m相對誤差而確定的，其具體表達式為

式中，cal為求解域范圍。

磁場能量相對誤差m所描述的是有限元法對泛定方程的求解精度，或將數值解J代入泛定方程后，等號兩側的程度，當現有磁場能量相對誤差m大于目標精度m,tar時，需要對場量變化較大位置的單元進行再次剖分。而表3中的單元數與節點數是在繞組截面區域單元邊長上限為0.05mm、空氣區域單元邊長上限為1mm、磁場能量誤差目標精度m,tar為10-6、再剖分規模為30%的前提下的剖分結果。平面變壓器12層實驗模型在3次再剖分后，m達到6.4×10-7，繞組區域單元邊長減至0.026mm左右，空氣區域單元邊長則減至0.2mm左右。平面變壓器4層實驗模型在通過4次再剖分后，m達到2.0×10-7，繞組區域單元邊長減至0.018mm左右，空氣區域單元邊長則減至0.3mm左右。

（4）前處理時間指的是從模型繪制結束至單元剖分結束所需時間，受軟件精度顯示限制，表3中僅列出精確至秒的前處理時間數據。所采用的剖分方法為三角自適應（Triangular Adaptive Uniform, TAU）法。

（5）表3中存儲量占用物理量的具體構成為系數矩陣、解向量、常數項列向量三者存儲量占用之和。所采用的矩陣存儲形式為Matlab軟件中的Sparse存儲法。

通過與2D有限元法對比可知，本文方法減少了平面變壓器12層實驗模型約65%的計算時間以及約70%的存儲量，減少了平面變壓器4層實驗模型約60%的計算時間以及約66%的存儲量。這是由于在符合磁場強度一維分布的弱邊緣效應區域，相比于三角形單元，一維線性單元可以通過較少的節點場量對較大求解區域的電磁場進行離散剖分，從而減少了描述求解域場量分布所必需的單元數與節點數。

表3中顯示，本文方法描述平面變壓器12層實驗模型的弱邊緣效應區域僅需120個節點與119個單元，描述4層實驗模型的弱邊緣效應區域僅需48個節點與47個單元，然而2D有限元法描述平面變壓器12層實驗模型的弱邊緣效應區域所需節點數高達17 581，單元數則高達34 868，而描述平面變壓器4層實驗模型的弱邊緣效應區域所需節點數則高達8 312，單元數則高達16 422。

節點數與單元數的減少對線性方程組構成與求解過程主要產生如下三方面影響。

（1）節點數的減少意味著線性方程組系數矩陣階數的減少，有效地減少了此階段的計算時間。

（2）單元數的減少決定了貢獻矩陣數目的減少，在減少存儲資源的同時，也減少了系數矩陣構建的時間。

（3）單元數與節點數共同決定了線性方程組系數矩陣的復雜程度，本文方法同時減少單元數與節點數使得存儲系數矩陣所需的存儲資源減少。

綜上所述，在處理平面變壓器電磁場求解這一問題中，通過本文方法可以有效地減少2D有限元法的單元數與節點數，從而節約了線性方程組構建與求解過程的計算資源與存儲資源。

3.3 計算精度對比

通過Agilent E4980A阻抗分析儀對平面變壓器12層模型交流電阻與漏感進行實驗測量如圖9所示。測試過程中平面變壓器模型二次側短路，輔助繞組開路，忽略勵磁電感的影響，依據變壓器Γ型等效電路可以得到變壓器一次、二次側交流電阻之和ACs和一次、二次側漏感之和ss的實驗值。

為實現對繞組損耗計算精度的驗證，還需將實驗所得一次、二次側交流電阻之和ACs進一步轉化為繞組損耗，繞組損耗實驗值Cum表示為

圖9 E4980A阻抗分析儀與平面變壓器12層驗證模型

繞組損耗實驗值PCum與計算值PCuc的對比如圖10所示，傳統2D有限元法和本文方法繞組損耗相對誤差dP如圖11所示，漏感實驗值Lssm與計算值Lssc的對比如圖12所示，交流漏感相對誤差dL如圖13所示。

以實驗值Cum、ssm為基準值計算得到繞組損耗以及一次、二次側漏感之和的相對誤差P、L，其正值代表計算值小于實驗值，負值代表計算值大于實驗值，表達式為

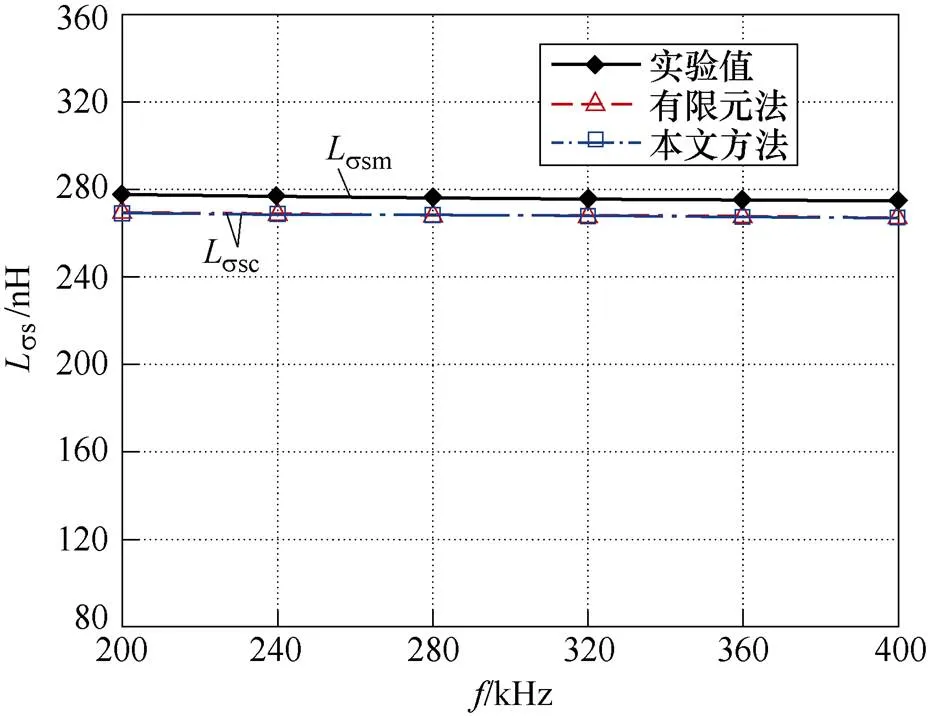
圖12 平面變壓器12層模型漏感實驗值與計算值對比

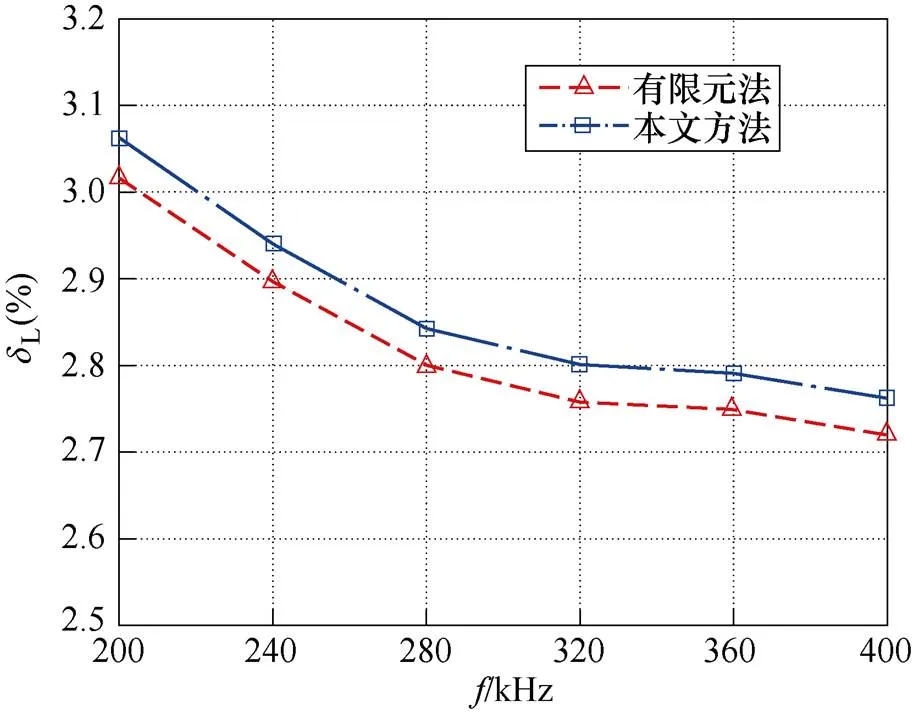
圖13 平面變壓器12層模型交流漏感相對誤差對比

由圖10～圖13可知，與2D有限元法相比，本文方法對平面變壓器12層實驗模型繞組損耗相對誤差P的提升最高處約為1.32%，對交流漏感相對誤差L的提升最高處不足0.10%。當然，不可否認的是，這與漏感ss因主要受導體外分布的磁場能量影響而受頻率變化影響較小有關。

通過Keysight E4990A阻抗分析儀對平面變壓器4層模型交流電阻與漏感進行實驗測量如圖14所示。

圖14 E4990A阻抗分析儀與平面變壓器4層驗證模型

平面變壓器4層模型的Cu實驗值與計算值的對比如圖15所示，傳統2D有限元法和本文方法繞組損耗相對誤差P如圖16所示，ss實驗值與計算值的對比如圖17所示，交流漏感相對誤差L如圖18所示。

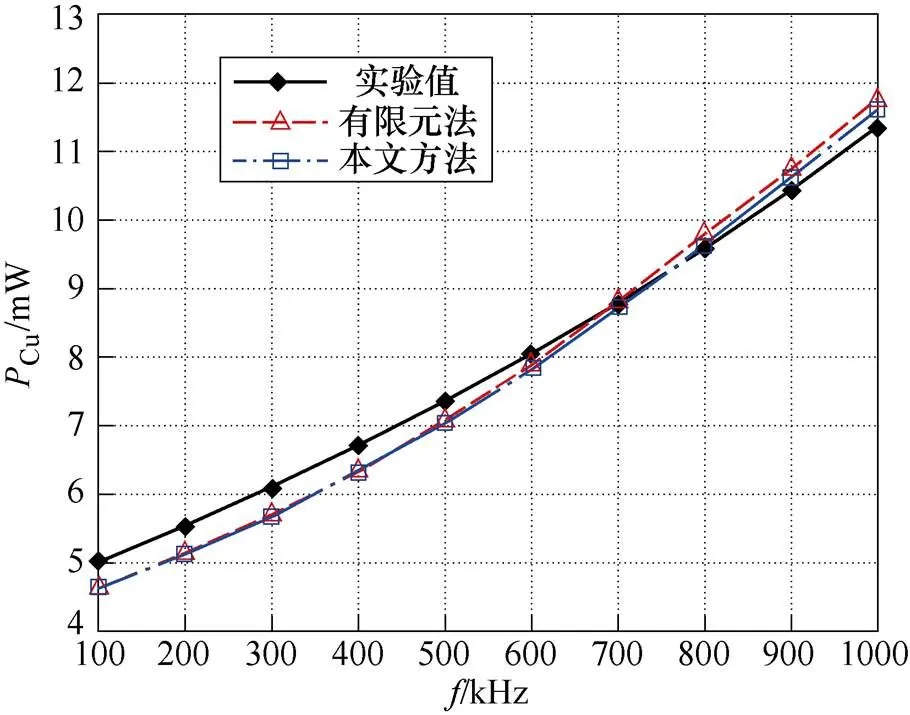
圖15 平面變壓器4層模型繞組損耗實驗值與計算值對比

由圖15～圖18可知，與2D有限元法相比，本文方法對平面變壓器4層實驗模型繞組損耗相對誤差P的提升最高處約為1.01%，對漏感相對誤差L的提升最高處不足0.10%。

綜上所述，無論是對2D有限元法在較窄頻率范圍內保障計算精度的平面變壓器12層模型，還是對2D有限元法在較寬頻率范圍內保障計算精度的平面變壓器4層模型，本文方法對2D有限元法的計算精度幾乎均未產生影響，與此同時本文方法卻具有較低的計算成本，因此可以驗證本文方法的有效性。

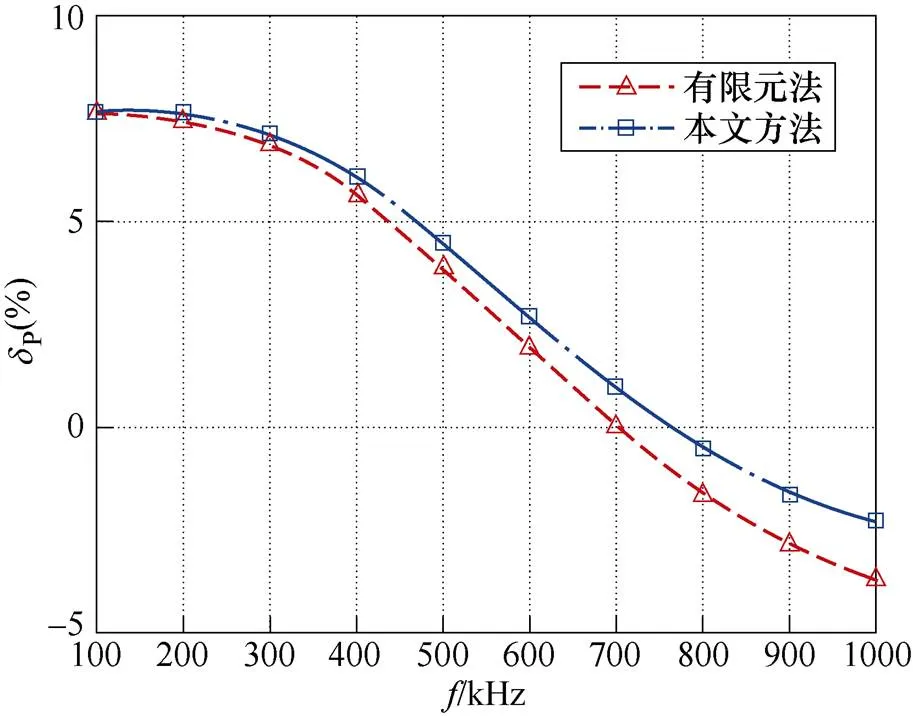
圖16 平面變壓器4層模型繞組損耗相對誤差對比

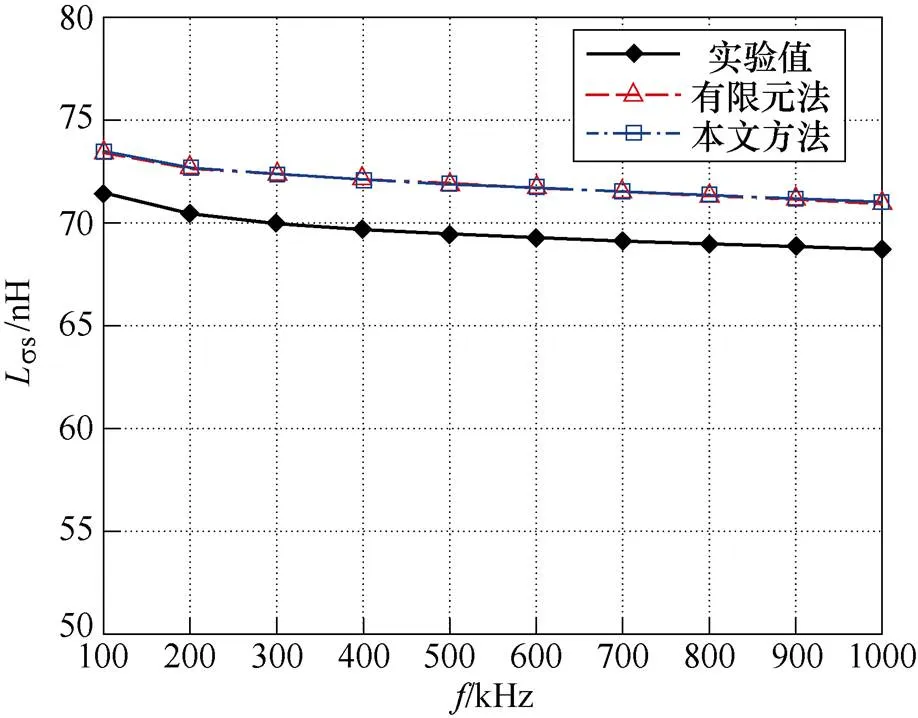
圖17 平面變壓器4層模型漏感實驗值與計算值對比

圖18 平面變壓器4層模型交流漏感相對誤差對比

4 結論

本文在2D有限元法的基礎上，針對平面變壓器繞組損耗與漏感參數精確計算問題，通過對求解域劃分并引入一維線性單元的剖分策略，提出一種針對線性方程組構建與求解過程計算且節約存儲資源的方法。并通過以上工作內容得出如下結論：

1）通過將求解域劃分為強邊緣效應區域與弱邊緣效應區域，并引入一維線性單元代替三角形單元對弱邊緣效應區域剖分離散的方法，能夠減少弱邊緣效應區域剖分所需的節點數與單元數，進而減少2D有限元法線性方程組構建與求解這一過程的計算時間與存儲占用。

2）依據平面變壓器磁場強度分布劃分求解域，并在符合磁場強度一維線性分布的弱邊緣效應區域應用與此區域契合度較高的一維線性單元，這種方法對2D有限元法對繞組損耗與漏感的計算精度幾乎不產生影響。

3）在前處理過程中，通過制定相鄰三角形單元與一維線性單元的剖分規則，即相鄰單元的節點相互重合而棱邊與節點不重合，能夠解決三角形單元與一維線性單元的單元兼容問題，并使得系數矩陣的構建過程能夠順利進行。

[1] 呂正, 顏湘武, 孫磊. 基于變頻-移相混合控制的L-LLC諧振雙向DC-DC變換器[J]. 電工技術學報, 2017, 32(4): 12-24.

Lü Zheng, Yan Xiangwu, Sun Lei. A L-LLC resonant bidirectional DC-DC converter based on hybrid control of variable frequency and phase shift[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 12-24.

[2] Shahabi A, Lemmon A N. Modeling of ZVS transi- tions for efficiency optimization of the phase-shifted full-bridge topology[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 529-544.

[3] Fei Chao, Li Qiang, Lee F C. Digital implementation of light-load efficiency improvement for high- frequency LLC converters with simplified optimal trajectory control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 1850-1859.

[4] Qian Ting, Qian Chenghui. A combined topology with coupled LLC resonance for wide-range operation[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6593-6600.

[5] 丁超, 李勇, 姜利, 等. 電動汽車直流充電系統LLC諧振變換器軟開關電壓邊界分析[J]. 電工技術學報, 2022, 37(1): 3-11.

Ding Chao, Li Yong, Jiang Li, et al. Analysis of soft switching voltage boundary of LLC resonant con- verter for EV DC charging system[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 3-11.

[6] Li Guangdi, Xia Jin, Wang Kun, et al. Hybrid modulation of parallel-series LLC resonant converter and phase shift full-bridge converter for a dual-output DC-DC converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(2): 833-842.

[7] Wu Hongfei, Li Yuewei, Xing Yan. LLC resonant converter with semiactive variable-structure rectifier (SA-VSR) for wide output voltage range application[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3389-3394.

[8] Wu Liang, Xiao Long, Zhao Jun, et al. Modelling and optimisation of planar matrix transformer for high frequency regulated LLC converter[J]. IET Power Electronics, 2020, 13(3): 516-524.

[9] 劉曉東, 董保成, 吳慧輝, 等. 基于并聯變壓器切換的LLC諧振變換器寬范圍效率優化控制策略[J]. 電工技術學報, 2020, 35(14): 3018-3029.

Liu Xiaodong, Dong Baocheng, Wu Huihui, et al. Wide range efficiency optimization control strategy for LLC resonant converter based on parallel trans- former switching[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3018-3029.

[10] 湯欣喜, 邢巖, 吳紅飛, 等. 兼顧穩態效率和暫態升壓能力的LLC變換器[J]. 電工技術學報, 2020, 35(4): 767-774.

Tang Xinxi, Xing Yan, Wu Hongfei, et al. An improved LLC converter considering steady-state efficiency and transient boost capability[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(4): 767-774.

[11] 李彬彬, 王志遠, 張丙旭, 等. 采用輔助變壓器的可調壓諧振零電壓零電流開關變換器[J]. 電力系統自動化, 2022, 46(7): 160-169.

Li Binbin, Wang Zhiyuan, Zhang Bingxu, et al. Voltage-regulatable resonant zero-voltage zero-current switching converter with auxiliary transformer[J]. Automation of Electric Power Systems, 2022, 46(7): 160-169.

[12] 袁宇波, 史明明, 舒良才, 等. 基于混頻調制的電力電子變壓器設計方法及實驗驗證[J]. 電力系統自動化, 2020, 44(22): 176-183.

Yuan Yubo, Shi Mingming, Shu Liangcai, et al. Design method and experimental verification of power electronic transformer based on mixed- frequency modulation[J]. Automation of Electric Power Systems, 2020, 44(22): 160-169.

[13] Rouhollah S, Martin O, Ali S M. Three-dimensional frequency-dependent thermal model for planar trans- formers in LLC resonant converters[J]. IEEE Transa- ctions on Power Electronics, 2018, 34(5): 4641-4655.

[14] Zhang Zhiliang, He Binghui, Hu Dongdong, et al. Multi-winding configuration optimization of multi- output planar transformers in GaN active forward converters for satellite applications[J]. IEEE Transa- ctions on Power Electronics, 2018, 34(5): 4465-4479.

[15] 林聰智, 何銘協, 任小永, 等. 基于矩陣變壓器的1MHz GaN LLC變換器[J]. 南京航空航天大學學報, 2018, 50(5): 695-700.

Lin Congzhi, He Mingxie, Ren Xiaoyong, et al. 1MHz GaN LLC resonant converter with matrix trans- former[J]. Journal of Nanjing University of Aero- nautics & Astronautics, 2018, 50(5): 695-700.

[16] Ho G K Y, Pong B M H. Multilayer flexible printed circuitry planar transformer with integrated series capacitance for an LLC converter[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(11): 11139- 11152.

[17] Zhang Zhiliang, Hu Dongdong, Ren Xiaoyong, et al. Multi-winding configuration optimization of multi- output planar transformers in GaN active forward converters for satellite applications[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(5): 4465-4479.

[18] Cove S R, Ordonez M, Luchino F, et al. Applying response surface methodology to small planar trans- former winding design[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 483-493.

[19] Li J, Water W, Zhu Boyuan, et al. Integrated high- frequency coaxial transformer design platform using artificial neural network optimization and FEM simulation[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4.

[20] Lotfi A W, Lee F C. Two dimensional field solutions for high frequency transformer windings[C]//Pro- ceedings of IEEE Power Electronics Specialist Conference-PESC '93, Seattle, 1993: 1098-1104.

[21] Fei Chao, Gadelrab R, Li Qiang, et al. High-frequency three-phase interleaved LLC resonant converter with GaN devices and integrated planar magnetics[J]. IEEE Transactions on Power Electronics, 2019, 7(2): 653-663.

[22] Shafaei R, Perez M C G, Ordonez M. Planar trans- formers in LLC resonant converters: high-frequency fringing losses modeling[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9632-9649.

[23] Spro O C, Mauseth F, Peftitsis D. High-voltage insulation design of coreless, planar PCB trans- formers for multi-MHz power supplies[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 8658-8671.

[24] 王議鋒, 劉瑞欣, 韓富強, 等. CLTLC多諧振變換器的磁集成方法[J]. 電工技術學報, 2021, 37(2): 380-388.

Wang Yifeng, Liu Ruixin, Han Fuqiang, et al. Magnetic integration method for CLTLC multi- resonant converter[J]. Transactions of China Electro- technical Society, 2021, 37(2): 380-388.

[25] 王澤忠, 全玉生. 工程電磁場[M]. 北京: 清華大學出版社, 2021.

[26] IEC 63093-9, Ferrite cores - guidelines on dimensions and the limits of surface irregularities - part 9: planar cores[S]. Brussels: CEN-CENELEC Management Centre, 2020.

Improved Finite Element Method of Winding Loss and Leakage Inductance for Planar Transformer Used in LLC Converter

1,21,2

（1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300401 China 2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province Hebei University of Technology Tianjin 300401 China）

The finite element method is often used to accurately calculate the performance parameters such as winding loss and leakage inductance of planar transformers. However, due to high storing and calculating costs, in the case of a tight design cycle, the number of design schemes that can be accurately calculated is limited, which increases the risk of selecting the local optimum point as the final design scheme. Therefore, the process of constructing and solving linear equations that occupy many resources is improved. Firstly, by analyzing the magnetic field intensity distribution of the planar transformer, according to the strength of the edge effect, the solution region of the planar transformer is divided into the strong edge effect region and the weak edge effect region. Secondly, a one-dimensional linear element that is more suitable for the weak edge effect region is introduced to reduce the number of nodes and elements necessary to describe the solution region’s field, saving computing and storing resources. Thirdly, by restricting the distribution of adjacent element nodes, the problems of element compatibility and coefficient matrix construction caused by the introduction of one-dimensional linear elements are solved. Finally, planar transformer models are built. The winding loss and leakage inductance of calculated and experimental values, as well as the calculating and storing costs of the proposed method and the finite element method, are compared, which verifies the proposed method.

Planar transformer, finite element method, winding loss, leakage inductance, numerical methods

10.19595/j.cnki.1000-6753.tces.220253

TM433

國家自然科學基金（51677052, 52077053）和河北省人才工程培養（A201902009）資助項目。

2022-02-23

2022-05-07

趙志剛 男，1981年生，教授，博士生導師，主要研究方向為電工磁材料磁性能模擬與工程電磁場數值仿真及應用。E-mail: zhaozhigang@hebut.edu.cn（通信作者）

張學增 男，1995年生，碩士研究生，主要研究方向為電工磁材料磁性能模擬、電力電子磁性器件設計與工程電磁場數值仿真及應用。E-mail: hebutzhangxz@126.com

（編輯 陳 誠）