織物透氣性對火星用降落傘氣動特性影響機理

徐欣，賈賀，陳雅倩,4，榮偉，蔣偉，薛曉鵬,*

1. 中南大學 航空航天學院，長沙 410083

2. 南京航空航天大學 航空學院，南京 210016

3. 北京空間機電研究所，北京 100094

4. 浙江大學 航空航天學院, 杭州 310058

中國首次火星探測任務“天問一號”探測器于2021年5月15日成功著陸火星,火星探測任務中探測器的進入、減速和著陸(Entry，Descent and Landing, EDL)過程是實現其火星表面軟著陸的關鍵，而火星降落傘就在這一過程中起著至關重要的減速和穩定作用[1-3]。目前，已經成功的火星探測用降落傘均為盤-縫-帶傘[1]。隨著火星探測任務的深入推進，載荷的增加必將對火星降落傘的阻力性能提出更高的要求，可是單級盤-縫-帶傘在火星科學實驗室探測任務(Mars Science Laboratory，MSL)中已經達到其尺寸極限[4-6]，NASA已將超聲速盤帆傘和環帆傘作為未來火星探測任務的候選傘型[1]，然而目前這兩種傘型的飛行試驗全部失敗，究其原因可能在于該類傘型擁有復雜的透氣特性，即復雜的幾何透氣結構和柔性織物透氣。

起初，研究者僅關注傘衣的幾何透氣性(人為地改變傘面結構如開縫隙等方式)，而忽略了織物透氣性(織物兩側存在壓差時，單位時間通過單位面積織物空氣的體積)對降落傘氣動特性的影響。1955年，Goglia等通過大量試驗數據的統計分析揭示了傘衣織物透氣量方程和多孔介質滲流理論中的Ergun公式具有一致的形式[7]，這為傘衣織物透氣性的研究提供了理論基礎。隨后的風洞試驗表明：傘衣織物透氣性會隨著雷諾數的降低而顯著降低[8]；隨著循環載荷的增大亦會降低傘衣的織物透氣性[9]。值得注意的是，針對火星用環帆傘和盤-縫-帶傘的傘衣織物透氣性影響研究，通過引入有效孔隙率(氣體通過織物材料的平均速度與自由流速度之比[10])和總孔隙率(綜合表征織物透氣性和幾何透氣量)進行了大量亞聲速風洞試驗，明確了總孔隙率與傘衣阻力系數的函數關系[2,11-14]，并以此準確估算了亞聲速條件下全尺寸火星探測用降落傘的阻力性能。關于超聲速條件下織物透氣性的影響機理研究，僅有Taguchi等[15]開展的風洞試驗發現織物透氣性的提高會降低阻力系數，同時可以降低降落傘阻力的波動；另外，目前針對傘衣織物透氣性的數值模擬亦主要基于Ergun公式開展透氣性模型研究[16-18]，且大多集中在亞聲速條件。

綜上所述，亞聲速條件下織物透氣性對降落傘的氣動特性具有顯著的影響作用，且其在循環載荷和雷諾數等影響下的動態變化復雜，而對超聲速條件下織物透氣性的影響機理至今尚不清楚且報道較少。因此，對降落傘織物透氣性進行理論分析，可以為新一代超聲速降落傘的研制提供理論參考。本文將利用數值模擬手段，將透氣性傘衣等效為多孔介質，并從傘衣厚度和相對透氣量等關鍵設計參數角度，來研究超聲速和亞聲速條件下傘衣的織物透氣性影響機理，進而對比分析不同速域下傘衣的織物透氣性對探測器-降落傘雙體系統的氣動性能的影響差異，這對于火星降落傘的織物透氣性設計有一定的理論參考價值。

1 降落傘系統模型

由于超聲速盤帆傘和環帆傘的飛行試驗全部失敗，而MSL降落傘有豐富的風洞試驗數據，故本研究以文獻[11]中提供的三維剛性MSL降落傘系統模型為研究對象，該系統由盤-縫-帶傘(圖1(a))和前體探測器(圖1(b))兩部分構成，盤-縫-帶傘名義直徑D0為21.35 m，幾何透氣性為12.84%，前體探測器由迎風面的防熱罩和背風面的后截錐組成[19]，模型示意圖及尺寸如圖1所示。本研究中所有模型均進行6.7%縮比[12]，其他主要幾何參數在表1中列出。

表1 盤-縫-帶降落傘關鍵幾何參數[12]

2 來流條件及數值模擬方法

2.1 來流條件

文獻[20]開展了真實火星大氣環境對超聲速降落傘(未考慮透氣性)的影響機理研究，結果表明：真實火星大氣影響下，傘前激波的脫體距離減小，前體尾流與傘前激波的相互作用會減弱，然而，火星大氣成分對降落傘氣動性能和流場模式的影響有限。因此，本文作為織物透氣性的初步探索研究，主要考慮低密度的大氣影響，亞聲速來流條件參考馬赫數Ma=0.4的風洞試驗[11]，超聲速來流條件參考MSL降落傘41 km高度的飛行試驗[21]，具體參數如表2所示。

表2 本研究所用的來流條件[11,21]

2.2 多孔介質滲透理論

需要特別說明的是，考慮到對于柔性降落傘，柔性變形會引起柔性織物材料中微觀孔隙的空間結構分布變化，隨之會導致傘衣的織物透氣性發生變化[9,22]。而且柔性降落傘的傘衣織物密度、彈性模量等參數均會對流場的變化產生影響，這會導致流場的影響要素過多，難以控制單一變量總結出規律性結論，因此本文作為降落傘織物透氣性研究的第1步，首先將具有織物透氣性的傘衣等效為剛性多孔性介質材料進行數值模擬，后續研究將會基于剛性降落傘的流場規律進一步考慮柔性變形的影響。

基于多孔介質理論中經典的Ergun公式(Darcy-Forchheimer法則)[23]，其控制方程可表達為

(1)

式中：ΔP為多孔介質兩側壓差；μ為空氣黏度；ρ為空氣密度；D為表征透氣性介質中孔隙尺寸的特征長度；L為介質厚度；ε為多孔介質相對透氣量，即多孔介質中空隙所占體積與介質總體積的比值(計算方法可參考文獻[17])；V為透氣量，也即等價于該壓差下氣流垂直通過織物的速率，即透氣率，一般以L/(m2·s)或mm/s為單位。

當假定降落傘織物材料的孔隙度恒定時，式(1)可重新表達為

(2)

式中：

(3)

(4)

K1和K2分別稱為黏性因子和慣性因子，分別表征黏性耗散和動能損失[17,24]，其取決于多孔介質微觀幾何特性。

具體來講，針對多孔介質理論的微觀體現，多孔介質中的壓降主要由黏性阻力和慣性阻力所致，即：一種是由黏性引起的摩擦損失，與來流的速度及黏度成正比，K1為其修正系數，其受材料內部孔隙的表面積影響，傘衣材料的孔隙數量增加和孔隙直徑的減少均會導致流體黏性耗散的增加；另一種則是由多孔介質的阻礙作用引起的流體動能損失，與來流的動能成正比，K2為其修正系數，其主要受材料孔隙的曲率影響，孔隙曲率的增加會提高流體的動能損失，與K1相似，孔隙數量的增加也會增加動能的損失[25]。

在數值仿真過程中，由于來流的黏性和密度都是確定的，因此式(1)可以進一步表達為

(5)

式中：

(6)

(7)

將傘衣織物的多孔介質看作孔隙率均勻分布且各項同性的介質，根據寧雷鳴等[17]對傘衣織物的簡化透氣性預測方法，可以得到黏性系數a和慣性系數b的表達式為

(8)

(9)

相應地，由a和b的表達式可以得到黏性阻滯系數rv和慣性阻滯系數ri的表達式為

(10)

(11)

由此可見，多孔介質的透氣性參數rv和ri僅由傘衣的厚度和相對透氣量決定。

2.3 織物透氣性模型

對于流經傘衣的流體，由于傘衣存在織物透氣性，勢必會導致流體在傘內外存在壓力下降，并形成兩種“阻力”作用(黏性阻力和慣性阻力)。在流體計算中的動量方程添加了這兩種阻力源項，來描述傘衣的織物透氣性對流場的影響，其表達式為

si=avi+b|v|vi

(12)

式中：v為流體速度。修正后的動量方程可參考文獻[26]。

需要說明的是，目前超聲速可壓縮流動中可依據的透氣性理論尚不成熟且仍在發展，而最近NASA學者采用Darcy-Forchheimer法則(Ergun公式)開展了超聲速環境下的火星降落傘透氣性數值研究，并驗證了該方法的有效性[27]；同時本研究將對亞聲速可壓縮流動(Ma=0.41)下的透氣性傘衣采用Ergun公式進行模擬驗證(見2.4節)，所得數值模擬結果與風洞試驗結果吻合較好，另外，文獻[28]開展了Ma=0.5(目前可供驗證的風洞試驗最高馬赫數)的透氣性模擬驗證，這些均說明Ergun公式在針對火星降落傘的透氣性問題仍具有一定的適用性。綜上所述，作為對透氣性傘衣研究的初步分析，本文僅考慮不同織物透氣性下傘內的流場分布與整體的阻力性能和穩定性能，故仍以Ergun公式對火星降落傘進行理論分析，下一步將對Ergun公式進行更深入的研究驗證和修正。

另外，大量風洞試驗研究表明降落傘的穩定性和阻力性能受馬赫數和孔隙率顯著影響[1]，故本文分別在亞聲速和超聲速不同馬赫數來流條件下，通過厚度和相對透氣量兩個自變量來探究織物透氣性在不同馬赫數下對降落傘氣動性能的影響。

2.4 數值模擬方法及其驗證

采用有限體積法進行空間離散，控制方程為三維可壓縮理想氣體N-S方程，利用HLLC(Harten-Lax-van Leer-Contact)格式計算無黏通量，時間格式采用雙時間步隱式推進方法，同時選用TVD(Total Variation Diminishing)格式進行多項式插值來提高計算精度，亞聲速時間步長選用2×10-5s，而超聲速來流下，為捕捉更加精確的非定常流場結構，時間步長縮短至1×10-5s，入口邊界條件設置為遠場來流，出口邊界參數采用中心差分，壁面設置為無滑移絕熱壁面。已有研究表明，對于剛性降落傘采用層流模型的計算結果亦可與試驗結果吻合較好[29]，故本計算模型采用層流模型。

為保證數值模擬的準確性，建模時采用三維結構化黏性網格進行繪制，圖2為相應的三維模型網格示意圖，壁面處進行網格加密處理，圖3為多孔介質與自由流場設置示意圖。

圖2 探測器-降落傘雙體系統的三維網格

圖3 傘衣的多孔介質區域網格[28]

采用的數值模擬方法已在前期研究[30]中進行了可行性驗證。在該流場計算方法基礎上進一步考慮多孔介質，其驗證模型選用文獻[14]中由PIA-C-7020D Type I材料所編織的傘衣的透氣性參數，根據本文發展的織物透氣性模型計算獲得該種材料的傘衣厚度及相對透氣量(表3)，另外采用文獻[14]的來流條件如表4所示，將數值模擬和風洞試驗的降落傘的平均阻力系數進行對比(表5)，發現兩者之間的相對誤差在允許的范圍之內，故考慮多孔介質后的數值模擬方法仍然可行有效。

表3 驗證算例采用的傘衣透氣性參數

表4 驗證算例采用的來流條件[14]

表5 數值模擬與文獻[14]結果對比

在上述考慮透氣性的數值方法驗證中同時開展了網格無關性驗證。如表6所示，發現粗糙網格(100萬網格數)計算結果與文獻誤差過大，中等網格(200萬網格數)和高精度網格(300萬網格數)計算結果與風洞試驗結果相比[14]誤差較小。考慮到計算效率，上述驗證模擬以及亞聲速條件下研究均選取了中等網格(200萬網格數)。另外，由于在超聲速來流下無風洞試驗數據，為更加精確地捕捉傘前激波附近的流場變化，將網格數量提升至350萬，該網格密度與前期研究[28,31]中的網格密度相似。

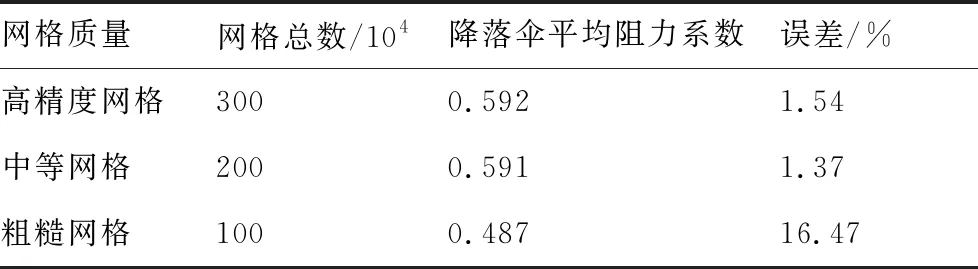
表6 不同網格計算與文獻[14]結果對比

3 亞聲速來流下織物透氣性影響機理

為衡量織物透氣性對降落傘氣動性能的影響大小及規律，分別以降落傘的阻力系數(CD)和橫向力系數(Cy)來衡量其阻力性能和穩定性能，計算方法為

(13)

(14)

式中：Fx為阻力；Fy為橫向力。

通過平均阻力系數來量化各傘型的阻力性能，阻力系數的標準差、橫向力系數的均值和標準差來量化對比穩定性能的優劣。

3.1 亞聲速傘衣相對透氣量影響

考慮到常用的傘衣材料相對透氣量一般是12%～20%，因此在數值模擬中，保持1 mm傘衣厚度，分別設計相對透氣量為8%、12%、16%、20%、24%的5組透氣性傘衣算例，并添加無透氣性傘衣(相對透氣量為0%)作為對比算例，計算結果如圖4所示。同時，為對比不同相對透氣量下，流場變化的差異性，分別截取每種相對透氣量傘衣下，阻力系數波動的一個完整波形對應的流線圖，如圖5所示。

由圖4(a)可以看出，亞聲速透氣性傘衣的阻力系數波動主要以低頻波動為主，這與超聲速來流下的波動模式存在較大差異(見4.1節)，這種低頻的波動主要是其流動模式所致：在亞聲速的來流條件下，傘內壓強升高，傘內外壓差提高，進而會提高傘衣透氣量，更多的流體流出傘衣，隨后，傘內外壓差降低，傘衣透氣量會下降，如此往復，體現為阻力系數的低頻波動。

由圖4(b)～圖4(e)可以看出，亞聲速來流下，透氣性傘衣相對透氣量的改變對降落傘阻力性能的影響并不明顯。但相比于透氣性傘衣，無透氣性傘衣由于傘內氣體缺少了從傘衣流出的這一泄壓方式，傘外壁處有附著渦的生成，傘外壓強更低，阻力系數相較于透氣性傘衣有較大的提高；同時，無透氣性傘衣僅僅通過頂孔和傘縫泄壓，傘壁處的流體全部集中涌向頂孔及傘縫處，泄壓方式的單一使得傘內壓強的變化頻率更高，這種流動模式下的無透傘衣的穩定性勢必會較透氣性傘衣有顯著下降，見圖5(a)～圖5(c)。

根據流線圖5(j)～圖5(r)可以看出，在相對透氣量16%以上時，傘衣處于一種高透氣流動模式，這種狀態下，傘內壁處的流體主要經由傘衣流向傘外，因此流體的縱向速度較高，傘內壁處流線主要以垂直于傘衣的方向流出傘衣，大幅抑制了傘內渦的形成，而因前體尾流的作用而形成的渦主要存在于遠離傘衣處，并且因縱向速度較大，很快消散。這種模式下，降落傘的阻力系數的波動程度較小，橫向力也處于一個較低的水平，降落傘的穩定性較高。

相比之下，相對透氣量8%的傘衣，其流場則處于低透氣流動模式，此時傘衣的透氣量只能允許小部分氣體流出，更多的氣體會涌向頂孔及傘縫處，如圖5(d)～圖5(f)所示，這會導致傘壁附近氣體存在更大的橫向流動，橫向力相較于高透氣性傘衣大，穩定性低。

圖4 亞聲速氣動力系數隨相對透氣量變化

圖5 亞聲速來流下不同相對透氣量流場結構對比

值得注意的是，當傘衣的相對透氣量處于12%時，傘衣處于一種臨界透氣流動模式，這種狀態下流場的流動模式呈現低透氣性模式和高透氣性模式混合的特征，即傘內流線出現縱向流動和橫向流動的交替轉換，這種轉換促成了內傘壁附近更容易有渦結構的出現，進而大幅影響了內傘壁處的壓強變化，阻力系數和橫向力系數的波動程度劇烈，如圖5(g)～圖5(i)所示。

3.2 亞聲速傘衣厚度影響

在探究傘衣厚度對氣動性能的影響時，考慮到常用傘衣厚度在0.2～1 mm，故控制傘衣的相對透氣量為12%，分別設計0.2,0.5,1,2,3 mm 這5組透氣性傘衣算例，氣動力系數的計算結果如圖6所示。

從流線圖上來看，亞聲速來流條件下，低于1 mm的傘衣被看作為一種低厚度狀態，這種狀態下，受到前體尾流的影響，傘內會有遠離傘壁面的小渦出現，但由于傘衣透氣量較大，傘內壁附近的流線主要呈現縱向流動，這種流動使得這些渦尚未到達內傘壁附近便消散了，大部分氣體由傘衣直接流出傘外，傘壁附近無明顯的渦結構生成，此時橫向力及其波動均處于較低值，如圖7(a)～圖7(f)所示。

如圖7(j)～圖7(o)所示，當傘衣厚度較厚時(高于1 mm)，此時傘衣處于一種高厚度狀態，從流線圖上來看，靠近傘壁處的氣體一部分會從傘衣處流出，但由于傘衣透氣量較低，還有一部分氣體會沿著傘衣內壁向傘縫處流動，并從傘縫處流出，此時亦可保持相對穩定的流動模式。

圖7 亞聲速來流下不同傘衣厚度流場結構對比

特殊的是，1 mm傘衣厚度下，處于一種低厚度流動模式和高厚度流動模式的臨界狀態，隨著傘內壓強的交替性變化，傘內壁處的流線亦呈現縱向流動和橫向流動交替性變化，這種流動模式的轉變使得傘內壁附近有渦的產生，如圖7(g)～圖7(i)所示，渦的產生和消散會造成傘內橫向力分布不均勻，進一步提高傘內力的波動，造成穩定性大幅下降。

4 超聲速來流下織物透氣性影響機理

4.1 超聲速傘衣相對透氣量影響

與亞聲速織物透氣性設計方案類似，在研究相對透氣量的影響時，選用1 mm厚度傘衣，同樣設計8%、12%、16%、20%、24%這5組透氣性傘衣算例以及一組無透氣性傘衣(相對透氣量0%)作為對比算例，計算結果見圖8，完整波動內對應的流場結果如圖9所示。

根據圖8(a)可以發現，和亞聲速透氣性降落傘阻力系數的波動模式相比，超聲速透氣性降落傘分別存在高頻和低頻兩種波動，低頻波動成因與亞聲速類似，不同的是增加了傘前激波的作用：傘內壓強升高，推動傘前激波向遠離傘體(上游)方向運動，致使傘內壓強降低，透氣量下降，阻力系數降低；傘內壓強的降低進一步促使傘前激波向傘內(下游)移動，傘內壓強逐漸升高，阻力系數升高，形成一個完整的低頻波動。

圖8 超聲速氣動力系數隨相對透氣量變化

圖9 超聲速來流下不同相對透氣量流場結構對比

而高頻波動作為超聲速流場獨有的波動形式，其成因根據流線圖9可以得出：由于前體窄尾流和激波的相互作用，作用點集中在中軸線附近，導致傘內中軸線附近流線出現小幅高頻波動，而遠離中軸線處的流線仍保持較為穩定的流動模式，傘內壓強無顯著變化，阻力系數的變化以小幅高頻波動為主。

由于弓形激波一直處于傘口附近，其與前體尾流的相互作用使得傘內處于高壓，此時多伴隨著傘內壓力的高頻波動；當相對透氣量越高，傘前激波愈靠近傘口(即脫體距離變小且波動較弱)，這使得傘內壓強的高壓狀態維持更長。因此，超聲速透氣性降落傘傘內處于高壓時段的時長明顯高于低壓時段。

總的來看，在超聲速的來流條件下，由于出現傘前激波與前體尾流的相互作用，傘內的渦量較亞聲速來流提升明顯，因此高頻的阻力僅出現于超聲速來流下；另一方面，亞聲速降落傘由于沒有了傘前激波的壓迫，傘內壓強將難以持續維持在高壓強區，高壓時段與低壓時段時長基本相等。

從圖9看可以看到，透氣傘衣傘后壓強明顯高于無透氣傘衣，且傘衣處由于有流線穿過，抑制了傘后附著渦的生成，對降落傘的穩定性產生積極影響。

對于透氣性傘衣，當傘衣的相對透氣量高于16%時，傘衣處于高透氣狀態，這一狀態下，傘衣透氣性較高，傘內渦量較小，這些渦主要是由傘前激波和前體尾流的相互作用而產生的，因此這些渦主要存在于遠離傘壁處，且小而分散，表現為較優的穩定性，見圖9(j)～圖9(r)。

如圖9(d)～圖9(i)所示，傘衣的相對透氣量低于12%時，此時的低透氣狀態下，傘內渦的形成原因主要是低透氣性傘衣對高速氣流的阻滯作用導致的，因此，此時傘內生成的渦大都是靠近傘內壁處，這會使降落傘的穩定性大幅下降。綜上，對于1 mm的透氣性傘衣，隨著相對透氣量由8%增加到24%，阻力系數的波動幅度呈現先升高后下降的趨勢，這可能是由于火星大氣環境中傘衣的臨界透氣量(如12%相對織物透氣量)對周圍流場的影響所致。

4.2 超聲速傘衣厚度影響

控制傘衣材料12%的相對透氣量，分別設計0.2、0.5、1、2、3、4 mm這6組不同厚度傘衣作為對比算例，氣動力系數對比如圖10所示。

根據圖11(a)～圖11(f)，當傘衣厚度小于1 mm時，傘衣處于一種低厚度狀態，該狀態下，傘衣內部靠近中軸線處由于前體窄尾流與傘前激波的相互作用，有較小渦生成，而遠離中軸線處流動模態則較為穩定，這一穩定狀態使得近傘壁處流線接近垂直的角度穿過傘衣壁面，而很少出現大角度偏轉的流線，這就大大削減了橫向力的大小和波動程度，從而提高了降落傘的橫向穩定性。

同時，這種高透氣性狀態下傘內壓強可以更容易地從傘衣泄出，抑制了傘內氣體集中涌向頂孔以及傘縫處的趨勢，傘內更容易維持在一個較平穩的流動狀態下，避免了傘內壓強的大幅度波動，這一狀態的維持使得傘內能夠長時間處于一個相對較高壓強的狀態，并伴隨有由前體窄尾流和傘前激波相互作用而導致的高頻波動。

圖10 超聲速氣動力系數隨傘衣厚度變化

如圖11(g)～圖11(r)所示，當傘衣厚度大于或等于1 mm時，此時傘衣處于一種高厚度狀態，該狀態下，傘衣內部的渦量大幅提升，渦的出現不僅僅局限于中軸線附近，而是擴散至整個傘內，傘內呈現較強的非定常流動模式，縱向力波動勢必提高；同時這種流動模式使得傘內流體獲得了更大的橫向力，內傘壁附近的流線大都與傘壁成一定角度，甚至存在接近平行于傘衣的流線，傘內渦出現明顯的橫向不均勻分布，降落傘的橫向力大小及其波動提高。

圖11 超聲速來流下不同傘衣厚度流場結構對比

同時，這種狀態下，隨著傘衣厚度的增加，根據式(10)和式(11)，材料本身對氣流的阻滯能力會下降，此時這種下降可能占據了主導，傘內壓強變化平穩，對傘的往復性沖擊變小，體現為傘前激波的脫體距離的運動幅度更小，激波位置更加穩定，降落傘的穩定性隨厚度增加而升高。

4.3 織物透氣性對穩定性的影響

1) 當觀察超聲速透氣性降落傘的橫向力系數時，發現橫向力系數隨時間的變化呈現比阻力系數更高頻率的波動，即使是穩定性較優的0.2 mm、相對透氣量12%盤-縫-帶傘衣，其傘內的壓強不均勻分布仍處于較高水平，如圖12所示。

2) 以超聲速來流下1 mm傘衣為例，相對透氣量8%及20%的橫向力系數隨時間變化的對比結果(圖13)可知，低織物透氣量的傘衣的橫向力系數隨時間變化頻率更高，變化幅值更大。而盤帆傘型的簡化模型可參考文獻[30]，傘面包含數目眾多的縫和隙結構，在NASA開展的高空飛行試驗[32-33]中，為了保持超聲速盤帆傘/環帆傘與盤-縫-帶傘總孔隙率相當，超聲速盤帆傘/環帆傘采用了比盤-縫-帶傘織物透氣性更低的傘衣，因此，盤帆傘/環帆傘內會呈現更大幅度的橫向波動。

3) 對1 mm傘衣的傘內上下各90個計數點的壓強大小進行觀察，得出傘內壓強的分布情況如圖14所示，結果發現靠近上部傘帶中點的a點呈現出明顯的應力升高，而傘盤上靠近頂孔處對稱的b、c點，其壓力也呈現明顯的不對稱分布。

圖12 0.2 mm厚度傘衣的橫向力系數隨時間變化

圖13 不同相對透氣量傘衣橫向力系數隨時間變化對比

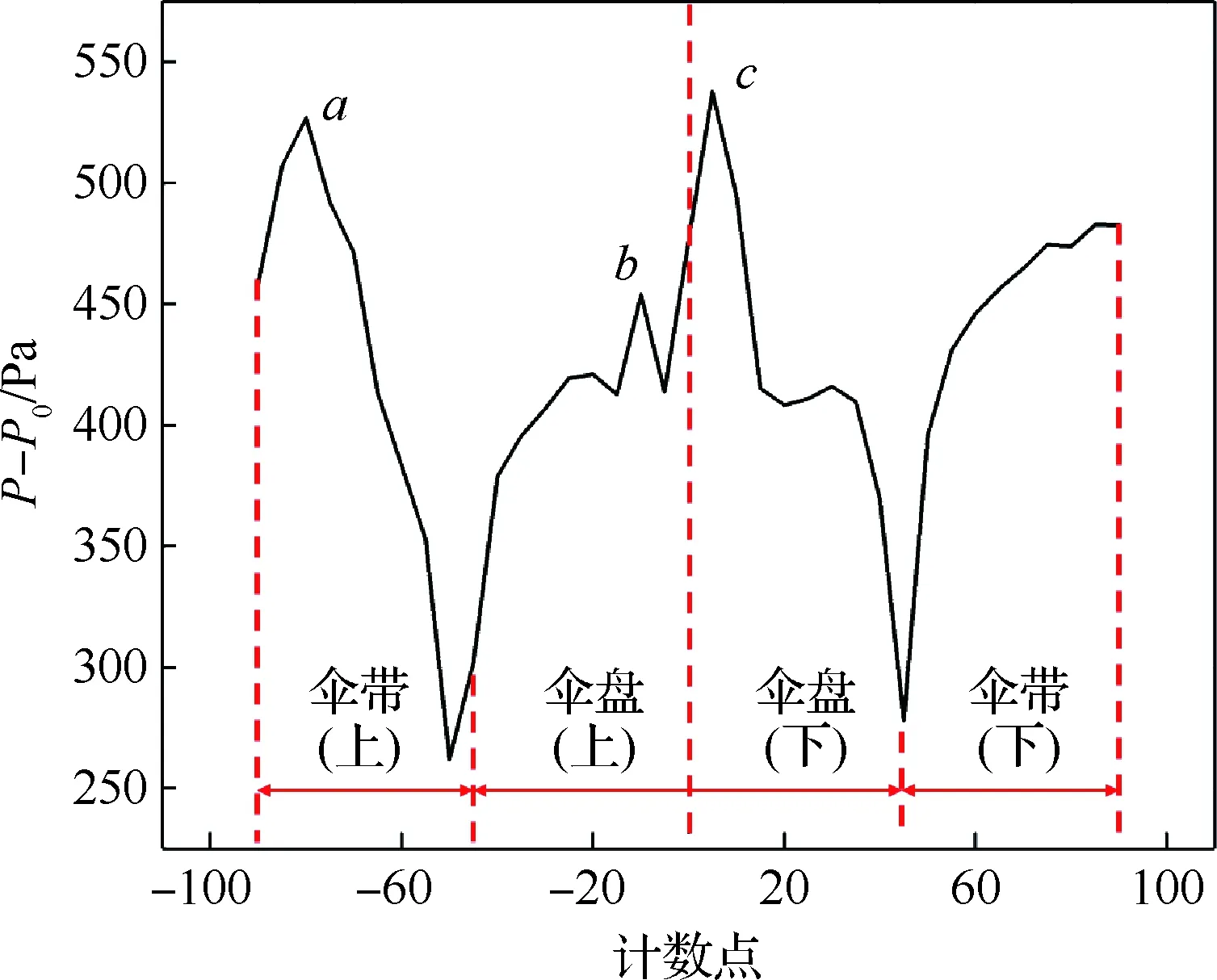
圖14 1 mm厚度傘衣的傘內壓強分布

綜上所述，對于透氣性分布更加復雜的超聲速環帆傘/盤帆傘，傘內壓力不均勻及應力集中問題將會比較嚴重，且在橫向波動較劇烈的情況下極易造成傘衣的某些區域壓力集中，使得傘衣出現傘衣失效和破裂。

5 結 論

利用數值模擬的方法，通過厚度和相對透氣量兩個自變量來探究織物透氣性在不同馬赫數下對降落傘氣動性能的影響。主要結論如下(其中結論1)～3)對于亞聲速和超聲速來流均適用)：

1) 總體來講，傘衣透氣性的加入可以將降落傘從結構縫隙單一泄壓模式轉變為結構縫隙/織物傘衣的雙重泄壓模式，故透氣性傘衣相較無透氣傘衣阻力系數下降顯著；相較而言，傘衣相對透氣量的增加，傘衣平均阻力系數總體呈現減小趨勢，但是由于透氣量的增加，其對傘內流場的復雜影響主要體現在壓力的波動變化，所以對阻力系數變化的波動程度影響較為明顯，但其影響程度低于透氣性的加入帶來的阻力性能變化。

2) 對于1 mm厚度的傘衣，相對透氣量處于16%～24%時，傘內流動模式更加穩定，對降落傘的穩定性有著較大提高，且阻力性能的損失較低。

3) 對于12%相對透氣量的傘衣，0.2～0.5 mm傘衣厚度能夠有效降低傘內的波動，對降落傘的穩定性有較大的提高，而厚度大于3 mm的傘衣雖然同樣可以達到較優的穩定性，但也會增加降落傘的重量。

4) 在本研究的低密度大氣環境中，厚度0.2～3 mm、相對透氣量8%～24%的透氣性降落傘在超聲速條件下工作時，前體尾流與傘前激波相互作用使得傘內處于高壓，此時可觀測到傘內壓力呈現高頻波動；當相對透氣量增加，傘前激波愈靠近傘口，傘內壓強的高壓狀態更持久，這使得傘衣阻力系數中的低頻大幅波動較亞聲速時有所抑制。總體來講，與亞聲速條件相比，超聲速條件下透氣性傘衣的阻力系數和橫向力系數波動均較小，穩定性較好。

鑒于NASA開展的超聲速盤帆傘(SSDS)和超聲速環帆傘(SSRS)飛行試驗[32-33]的失敗可能與其復雜的結構透氣性和織物透氣性有關，在未來的研究中將主要考慮：真實的火星大氣環境下，織物透氣性對超聲速火星降落傘的氣動特性的影響機理；在具有織物透氣性的降落傘基礎上進一步考慮結構透氣性的耦合影響，開展在相同的總孔隙率條件下，織物透氣性和結構透氣性分配比例的影響機理研究，從而設計氣動性能更加優異的孔隙率配比方案。