基于三階剪切計算連續性方法的編織復合材料板三尺度分析模型
萬傲霜, 王振名,李頂河
中國民航大學 航空工程學院,天津 300300
與傳統的多向層合復合材料相比,編織復合材料具有優良的面外性能,在航空航天、汽車和船舶等領域的應用日益廣泛[1-2]。美國航空航天局于1988年啟動先進復合材料技術(ACT)計劃,將編織復合材料應用于飛機結構(見圖1)[3-4]。編織復合材料也被大量應用于直升機,包括機身蒙皮、主旋翼槳葉、尾梁和尾槳等[5]。
編織復合材料性能不僅取決于組分材料的力學性能和纖維體積分數,還取決于介觀尺度上編織纖維束的幾何構型,需要采用介觀力學方法精確模擬計算編織復合材料的力學響應,這對計算能力提出了很高的要求。為了兼顧計算成本和計算精度,基于均勻化方法的復合材料多尺度分析得到了大量研究。Terada和Kikuchi[6]、Matsui等[7]采用相關變分表述,將均質材料的兩尺度建模方法用于具有精細周期性微觀結構的非均質材料。Smit等[8]提出了一種在宏觀/微觀尺度上均考慮材料黏彈性和大變形的均勻化方法。Feyel和Chaboche[9]采用多級有限元方法建立了新的復合材料多尺度模型,考慮了纖維和基體力學性能之間的差異。基于漸近均勻化理論[10-11],Ghosh等[12]建立了非均質材料(包括多孔材料和復合材料)的多尺度彈塑性分析的有限元模型。Miehe[13]基于精細尺度的位移場結果,分析了微觀結構線性位移、周期性波動和邊界常應力的全局變分問題。Cao[14]計算得到了復合材料彈性靜力學問題解的迭代兩尺度漸近展開式。Zhang等[15]利用多尺度有限元方法,建立了宏觀尺度位移與微觀尺度應力應變之間的關系。袁欣和孫慧玉[16]利用均勻化方法計算分析了三維編織復合材料在不同溫度下的恒溫松弛模量,并進一步建立了由恒溫松弛模量確定變溫松弛模量的一般方法。楊強等[17]基于多尺度漸進展開理論,對復合材料彈性問題控制方程進行尺度分解,建立了復合材料宏觀和細觀尺度響應之間的關聯。胡殿印等[18]采用通用單胞(GMC)方法,建立了平紋編織復合材料的宏細觀多尺度模型,通過與傳統有限元單胞模型的宏細觀力學響應分析計算結果對比,驗證了模型的正確性。

圖1 編織復合材料飛機結構件[3-4]
現有的均勻化方法研究大多集中于一階均勻化理論,該理論假設施加于計算胞元(CUC)或代表性體積元(RVE)的宏觀尺度變形梯度是常值,導致大尺寸CUC或大應變梯度情況下的數值模擬結果不夠理想。為了捕捉復合材料場梯度和微觀結構引起的局部效應,通過引入適當的高階校正量,進一步發展了二階均勻化理論,假設宏觀變形梯度在CUC求解域上線性變化[19-23]。
由于上述兩尺度分析方法難以捕捉編織復合材料這種具有復雜內部結構的復合材料在各尺度上的大量振蕩信息,有必要對編織復合材料進行三尺度分析,包括對纖維和基體的微觀尺度分析、對纖維束和基體的介觀尺度分析、對復合材料結構的宏觀尺度分析,大量學者對此開展了研究。Trucu等[24]、Abdulle和Bai[25]系統研究了采用不同偏微分方程三尺度問題的計算收斂性。Ma等[26]采用兩尺度漸近展開方法,得到了介觀尺度問題的特征函數和特征值,并進一步推導了均勻化單元函數,建立了3個尺度下均勻化系數和材料系數之間的關系。基于均勻化理論和多尺度漸近展開方法,Yang等[27-31]提出了一種研究非均質材料在微觀、介觀和宏觀尺度上耦合傳導輻射和熱力學問題的高階三尺度分析方法。但是,這種方法必須結合高階單元解和一致解來構造三尺度漸近解,限制了該方法的應用。
為了克服均勻化理論和廣義連續理論的局限性,文獻[32-35]提出了計算連續性(C2)方法,可以對有限大小非均質體進行粗尺度連續性描述,該方法的粗尺度控制方程在不相交胞元組成的計算連續域上表示,確定了胞元位置后,在細尺度上確定控制方程的弱形式。這種不進行尺度分離的多尺度分析方法可以在不假設細尺度胞元無限小的條件下提供細尺度信息,并且不需要高階連續性、高階邊界條件和引入新的自由度。最近,C2方法被應用于等效單層理論框架下的復合材料層合板多尺度分析[36-37]以及三階剪切變形理論(TSDT)框架下的混凝土結構和復合材料曲梁多尺度分析[38-40]。
因此考慮到編織復合材料的宏觀力學性能取決于細觀組分材料性能和介觀纖維束編織構型,為了在可接受的計算成本下準確計算編織復合材料的位移場和應力場,有必要建立三尺度有限元模型。因此,本文提出一種基于三階剪切計算連續性方法的編織復合材料板三尺度分析模型。采用基于TSDT的八節點四邊形板單元對宏觀尺度模型進行離散,推導三尺度三階剪切計算連續性(TOS-C2)方法及其有限元方程;構建編織復合材料板三尺度TOS-C2方法的計算框架,利用含夾雜三維立方體的數值算例,檢驗該方法的有效性;利用三尺度TOS-C2方法,模擬計算平面編織復合材料板的微觀、介觀、宏觀尺度位移場和應力場。
1 理論模型
1.1 三階剪切變形理論
首先三階剪切變形理論的位移假設為
(1)
其中:
(2)
式中:(x,y,z)為板上某一點的坐標;h為板的厚度;u0、v0、w0分別為中心面上一點(x,y)在x、y、z方向的位移;u1、v1分別為(x,y)的剪切轉角;?w/?x、?w/?y分別為(x,y)的彎曲轉角。根據位移假設,應變分量可推導為
(3)
其中:
(4)
由式(3)可以看出,橫向剪切應變沿板厚呈拋物線變化,并在板的上表面和下表面達到0,不需要使用剪切校正因子。外載荷的應變能和外力功可表示為
(5)
其中:
(6)
式中:C為剛度矩陣;A為面積;w為位移;εx、εy、εxy、εyz、εxz為應變分量;σx、σy、σxy、σyz、σxz為應力分量;q為面積力。式(5)為推導有限元方程的基礎。
層合板的本構關系為
(7)
式中:Cij為剛度系數。
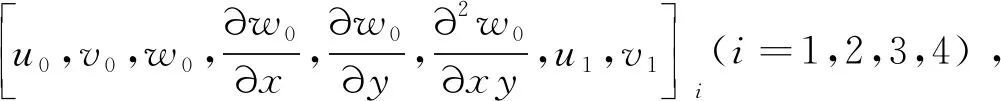
(8)

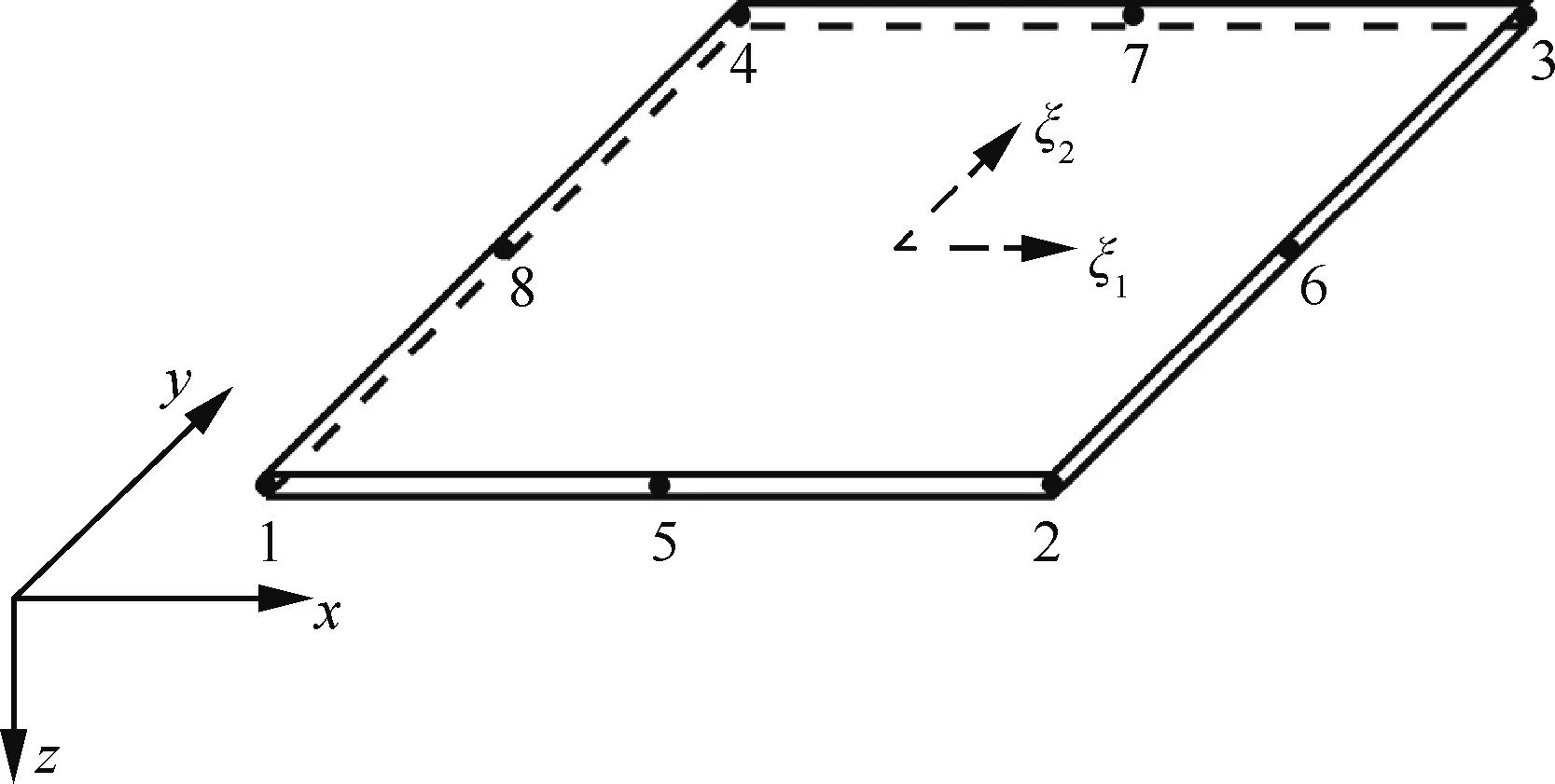
圖2 八節點四邊形板單元(坐標系原點位于板單元中心面上)
根據式(3),應變-位移的關系可寫為
(9)
式中:εp和εt分別為面內應變和彎曲應變;Lp和Lt分別為面內應變和彎曲應變的位移關系矩陣。
任意一點的位移矢量u可表示為
u=Nde
(10)
式中:[N]5×48為形函數矩陣,下標表示該矩陣的維度,具體表達式見附錄A;節點位移矢量[de]48×1為
(11)
式中:上標(i)為節點編號。
那么,面內應變和彎曲應變可以用節點位移矢量來表示
(12)
式中:Bp和Bt分別面內和彎曲為應變-位移矩陣,表達式為
(13)
總應變可寫為
(14)
[Bp]3×48、[Bt]2×48、應變-位移矩陣[B]5×48的表達式見附錄A。
1.2 三尺度計算連續性方法
基于C2多尺度方法的位移和應變分解,三尺度計算連續性模型的位移場和應變場分別可表示為
(15)
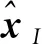
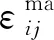
(16)
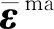
α,β,…,δ=1,2,3
(17)
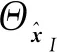
1.3 有限元方程
1.3.1 微觀尺度
由單絲纖維和基體組成的微觀尺度問題的弱形式定義為
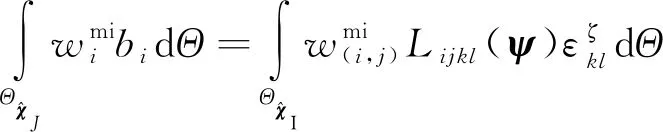
(18)
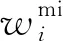
將微觀權函數umi和試探函數wmi用形函數Nmi(ψ)進行離散:
(19)
式中:dmi、cmi分別為權函數和試探函數的節點值。
將式(14)~式(16)、式(19)代入微觀尺度胞元問題的弱形式中,并且考慮到試探函數cmi的任意性,微觀尺度胞元問題權函數在節點處解的表達式為
(20)
式(20)可以簡寫為
(21)
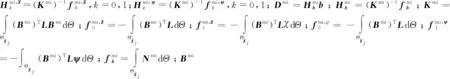
1.3.2 介觀尺度
由纖維束和基體組成的介觀尺度問題的弱形式定義為
(22)
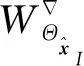
同樣地,將介觀權函數ume和試探函數wme用形函數Nme(χ)進行離散,表達式為
(23)
式中:dme、cme分別為權函數、試探函數的節點值。根據介觀應變的泰勒展開式,用權函數和試探函數對其進行表示為
(24)
其中:
α=1,2,3
(25)
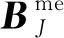
將式(16)、式(21)、式(24)代入介觀尺度胞元問題的弱形式中,并且考慮到試探函數cme的任意性,介觀尺度胞元問題權函數在節點處解的表達式為
(26)
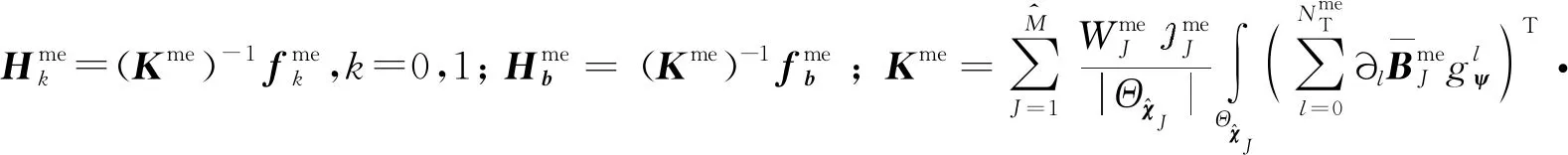
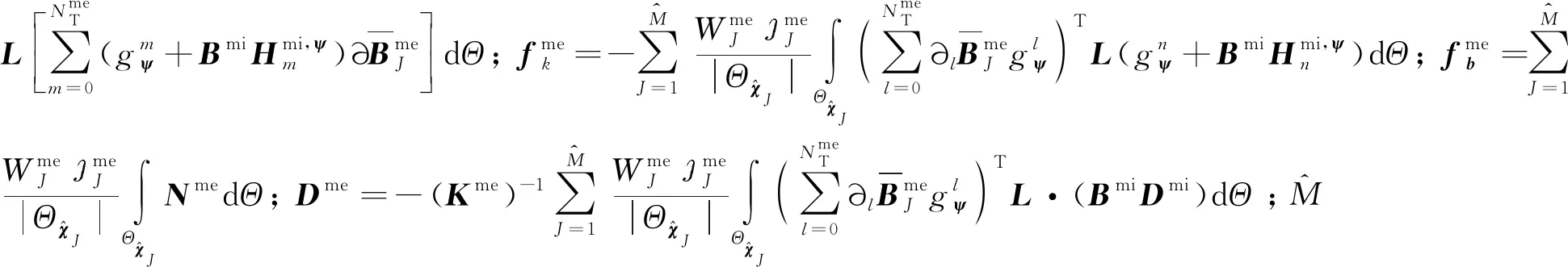
1.3.3 宏觀尺度
宏觀尺度問題的弱形式可定義為
?wma∈WΩx
(27)
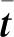
同樣地,將宏觀權函數uma和試探函數wma用形函數Nma(χ)進行離散,表達式為
(28)
式中:dma、cma分別為權函數和試探函數的節點值。根據宏觀應變的泰勒展開式,用權函數和試探函數對其進行表示為
(29)
其中
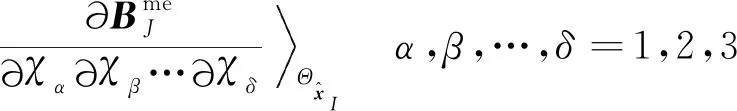
(30)
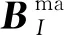
式(21)、式(26)可以寫為
(31)
(32)
式中:
(33)
將式(31)、式(32)代入宏觀尺度問題的弱形式中,并且考慮到試探函數cma的任意性,宏觀尺度問題權函數在節點處解的表達式為
dma=(Kma)-1fma
(34)
其中:
(35)
2 計算框架
圖3為三尺度三階剪切計算連續性(TOS-C2)
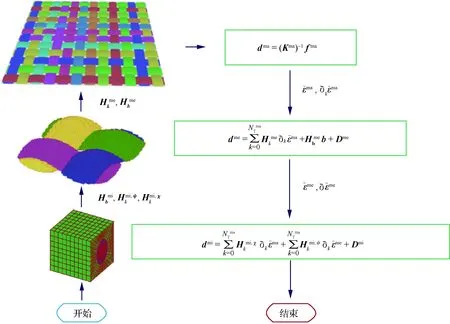
圖3 三尺度TOS-C2方法計算框架
方法的計算框架,具體流程如下:
1) 建立宏觀問題、介觀胞元和微觀胞元的有限元模型。
4) 由宏觀尺度模型的有限元方程,計算宏觀位移dma(見式(34))。
7) 后處理得所需尺度模型位移和應力分布。
基于Microsoft Visual Studio軟件,通過編寫程序實現上述計算框架。
3 數值算例
3.1 驗證算例
利用含夾雜的三維立方體算例來驗證所提出的三尺度TOS-C2方法。分別采用直接數值模擬(DNS)方法和三尺度TOS-C2方法建立有限元模型(見圖4、圖5),并進行對比分析。該驗證模型中的夾雜是指彈性模量較高的區域,類似微觀尺度上纖維束胞元模型的的單絲纖維。對于三尺度TOS-C2模型,微觀尺度胞元如圖4(a)所示;圖4(b)表示8個微觀尺度胞元組成的介觀尺度胞元模型夾雜域(見圖4(c))中的1個單元;整個介觀尺度胞元模型如圖4(d)所示。微觀和介觀尺度胞元模型均采用Hex8單元,其中介觀模型中采用非局部積分。由于1個宏觀尺度單元由4個介觀尺度胞元組成,宏觀尺度模型(見圖4(e))共包含256個介觀尺度胞元,分別在x、y方向有8個單元。對于DNS模型,單元尺寸則由微觀夾雜決定,整個DNS模型(見圖5(a))由夾雜(見圖5(b)、圖5(c))和基體組成。夾雜的材料屬性取彈性模量E=10.0 GPa,泊松比μ=0.3,基體的材料屬性取E=1.0 GPa,μ=0.3。宏觀模型的邊界條件為
(36)
將由DNS模型和三尺度TOS-C2模型計算得到的應力和位移結果進行對比分析,如圖6~圖8所示。從圖6中可以看出,三尺度TOS-C2模型計算得到的宏觀位移結果與DNS模型吻合良好,但宏觀應力計算結果存在一定偏差。為了將三尺度TOS-C2模型的介觀位移和應力結果與DNS模型進行對比,選取如圖4(e)所示一條線上的A、B、C作為分析對象。圖7、圖8、表1對比了介觀尺度胞元模型和DNS模型的位移及應力結果,可以看出2種模型的介觀尺度位移計算結果吻合良好,但應力計算結果存在一定偏差。需要指出的是,因為考慮到需要將DNS模型的計算量控制在可求解范圍內,網格劃分較為稀疏(TOS-C2介觀和微觀胞元模型分別為3×3×3和9×9×9單元數,而DNS模型中與介觀和微觀尺度相對應均采用3×3×3單元數),導致應力計算結果與DNS模型存在一定偏差,考慮到位移計算結果吻合良好,認為該模型的計算誤差在可接受范圍內。DNS模型和三尺度TOS-C2模型的單元數、節點數、計算時間和CPU數量見表2,可以看出三尺度TOS-C2模型在計算效率上有顯著優勢。此外,三尺度TOS-C2方法不僅可以有效分析含夾雜三維立方體的應力應變響應,由于該方法采用三階剪切變形理論,不存在剪切閉鎖問題,所以也能有效分析編織復合材料板的應力應變響應。
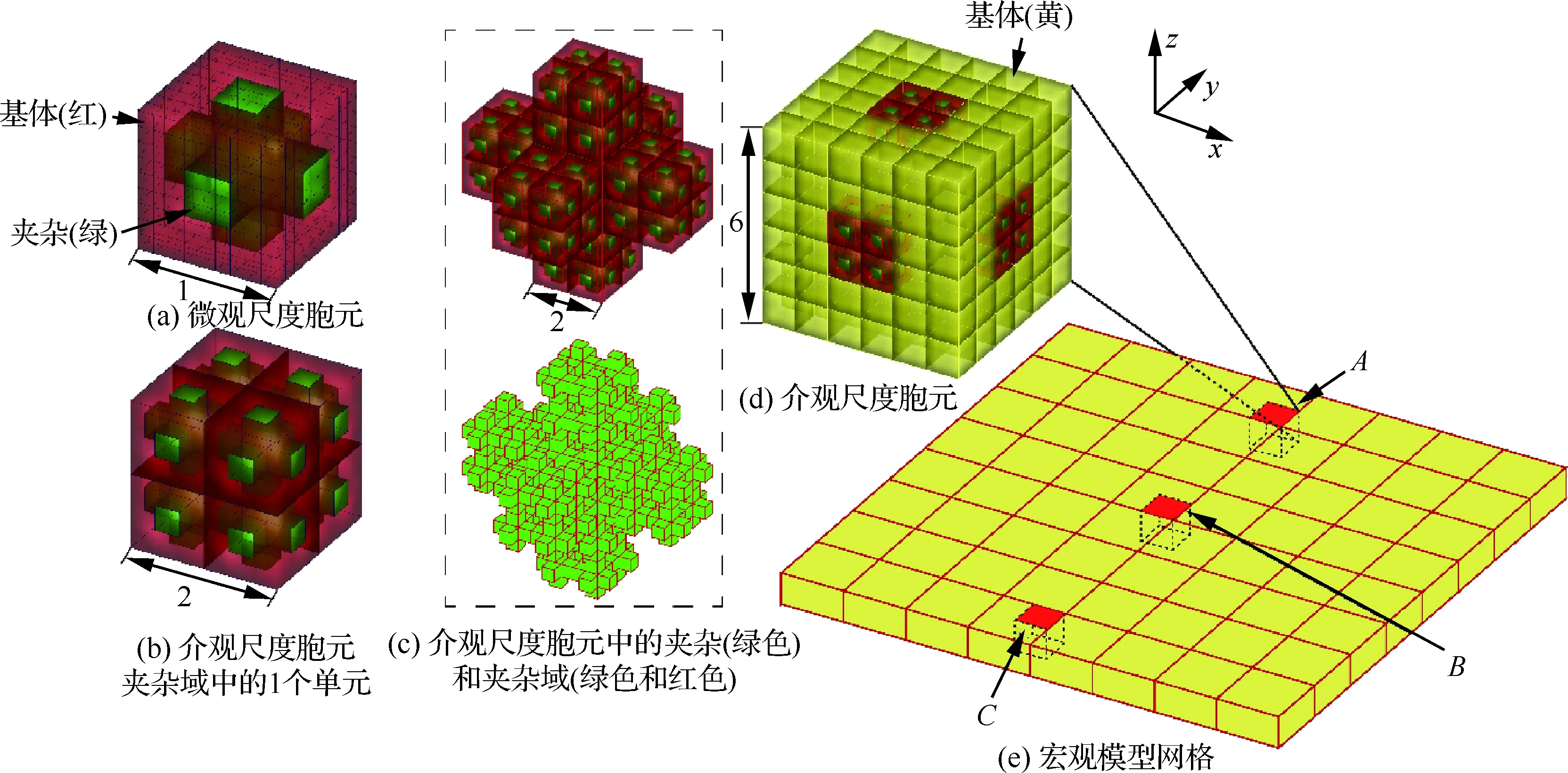
圖4 含夾雜三維立方體的三尺度TOS-C2模型
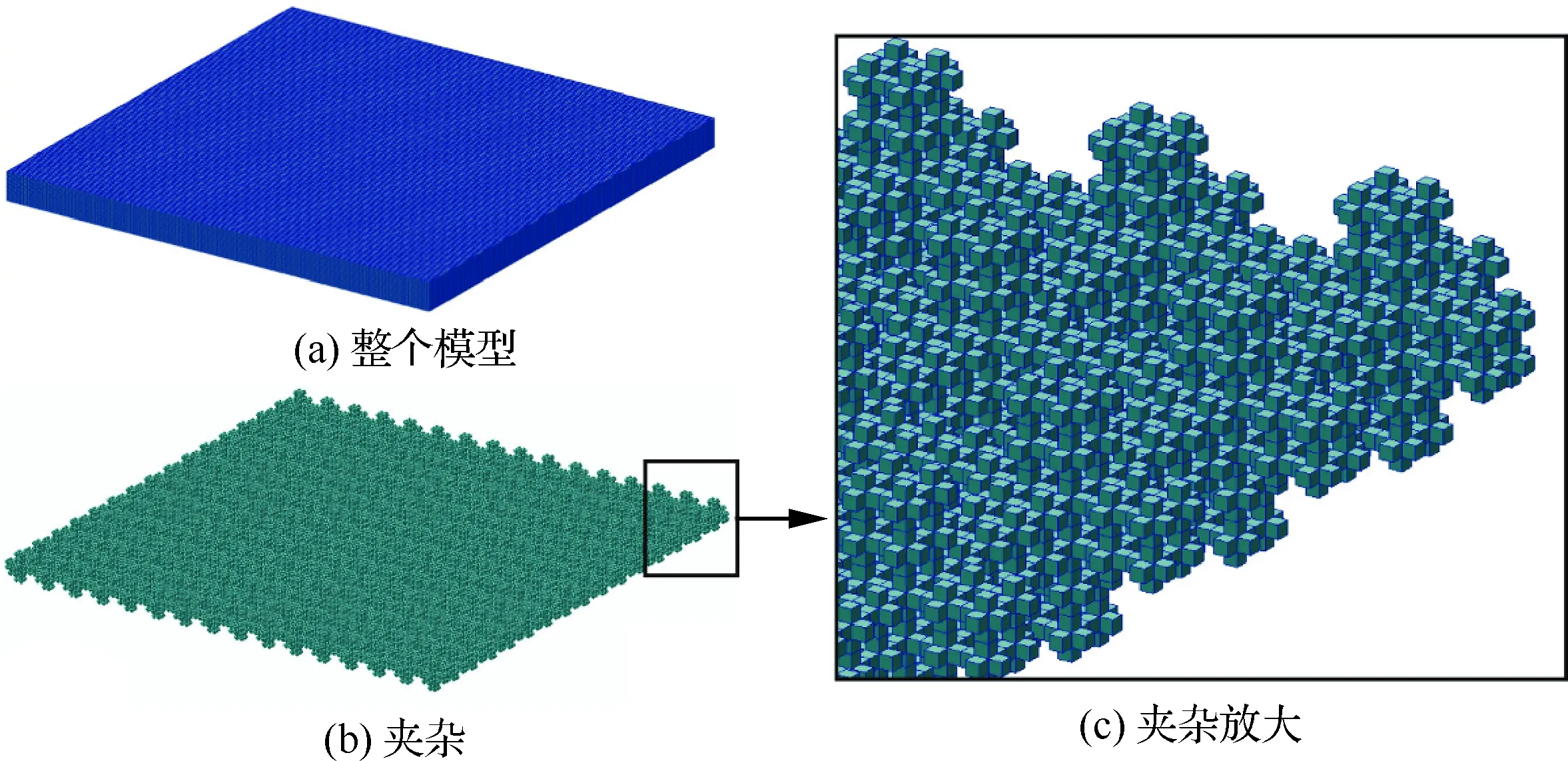
圖5 含夾雜三維立方體的DNS模型
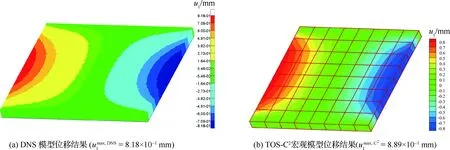
圖6 含夾雜三維立方體位移和應力計算結果

表1 含夾雜三維立方體A、B、C 3點處DNS模型和TOS-C2介觀胞元模型的位移和應力計算結果

表2 含夾雜三維立方體DNS模型和三尺度TOS-C2模型的計算量
3.2 平面編織復合材料板三尺度TOS-C2模型
圖9~圖11為采用提出的三尺度TOS-C2方法對平面編織復合材料板進行三尺度分析的過程和結果。圖9(b)為宏觀尺度模型(見圖9(a))中第25個單元的第4個積分點對應的介觀尺度胞元模型,分為2個部分,即介觀基體(見圖9(c))和編織纖維束(見圖9(d))。圖9(e)為放大后的介觀尺度纖維束,其中1個單元的求解域包含8個微觀尺度胞元(見圖9(f)、圖9(h)),圖9(g)、圖9(i)分別為8個微觀尺度胞元以及微觀尺度胞元中的單絲纖維。該三尺度模型中,介觀尺度和微觀尺度基體的材料屬性都是E=2.1 GPa,μ=0.3,微觀模型中單絲纖維的材料屬性為E=210 GPa,μ=0.3。宏觀尺度模型的邊界條件為四邊固支,并在底部施加均勻分布載荷p=1 Pa。
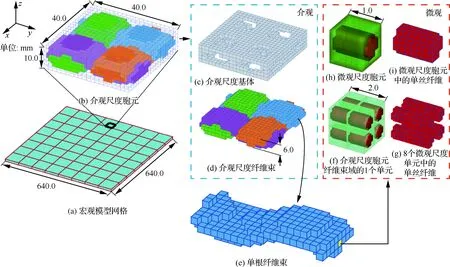
圖9 平面編織復合材料板的三尺度TOS-C2模型
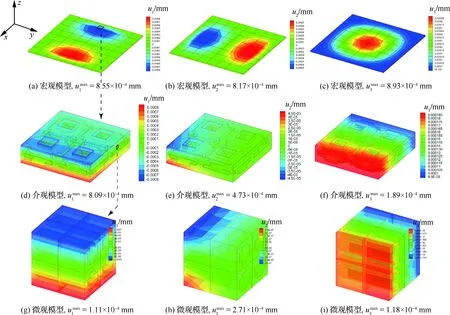
圖10 平面編織復合材料板三尺度TOS-C2模型的位移計算結果
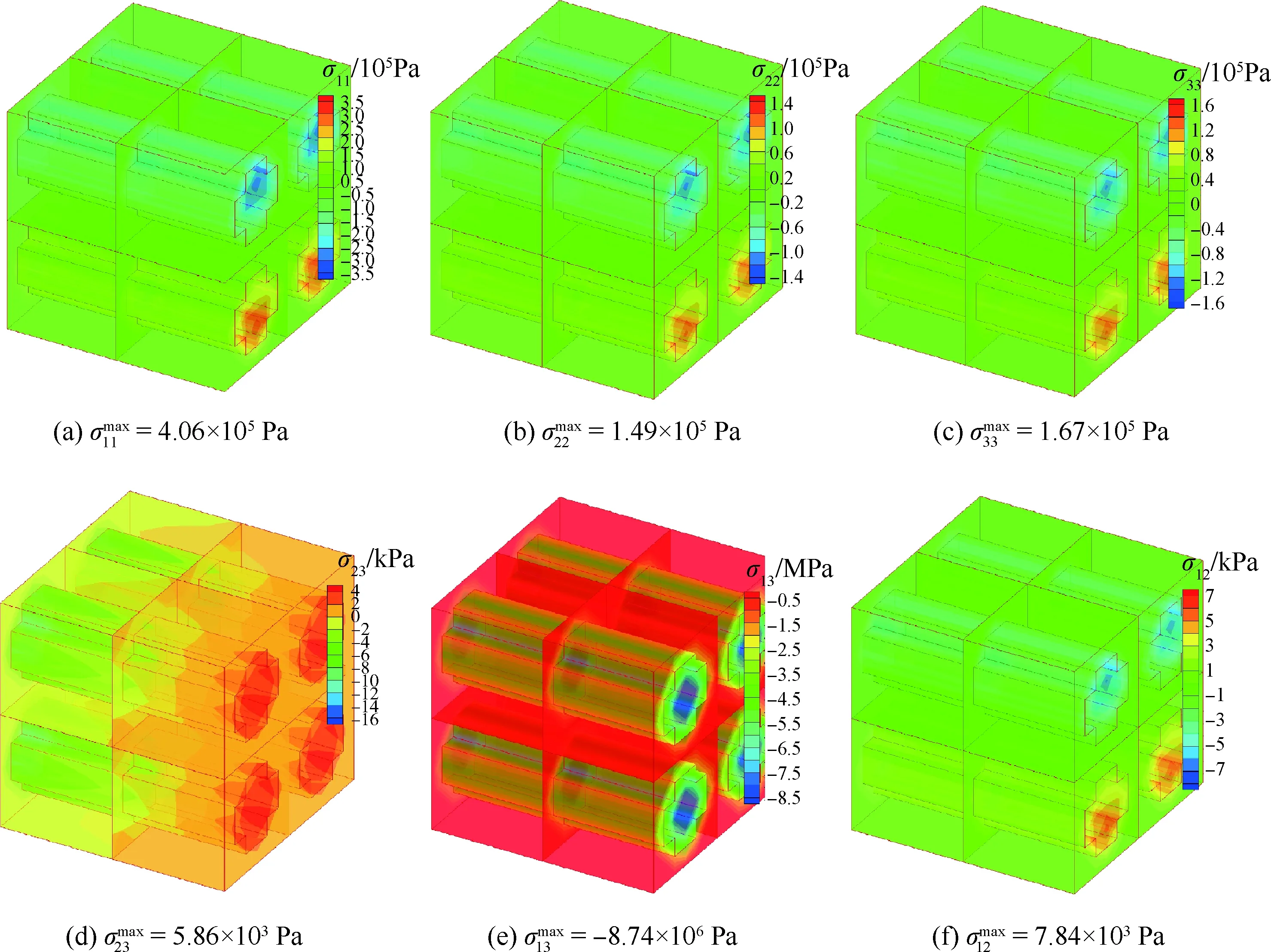
圖11 平面編織復合材料板TOS-C2微觀模型的應力計算結果

4 結 論
基于三階剪切變形理論(TSDT)和計算連續性(C2)方法,提出了新的編織復合材料板三尺度分析模型,得到如下主要結論:
1) 采用基于TSDT的八節點四邊形板單元對宏觀尺度模型進行離散,可以考慮剪切變形和沿厚度方向非線性剪切應變變化引起的轉動慣量。
2) 利用含夾雜三維立方體的數值算例,驗證了提出的三尺度三階剪切計算連續性(TOS-C2)方法的有效性,三尺度TOS-C2模型的位移和應力計算結果與直接數值模擬(DNS)模型吻合良好。
3) 提出的三尺度TOS-C2方法可以詳細描述編織復合材料板的微觀和介觀尺度結構以及三尺度位移和應力分布,為編織復合材料板航空航天結構設計和力學性能分析提供技術支持,并且,由于三尺度TOS-C2方法中宏觀和介觀尺度應變均采用泰勒級數展開,該方法可以適用于應力變化劇烈的復雜單元問題。

