基于新型權重解析法的永磁電機預測轉矩控制
顏黎明,郭鑫,趙冬冬
1. 長安大學 汽車學院,西安 710064
2. 西北工業(yè)大學 自動化學院,西安 710072
永磁同步電機(PMSM)以其高功率密度、高功率因數及高效率等優(yōu)點廣泛應用于航空航天行業(yè),多電飛機作動器、全電飛機電推進系統等領域[1-2]。在永磁同步電機控制理論方面,繼矢量控制和直接轉矩控制之后,有限集模型預測控制(FCS-MPC)以其概念直觀、動態(tài)響應快及易于處理多變量非線性控制等諸多優(yōu)點在電力驅動領域得到了學術界的廣泛研究[3-4]。有限集模型預測控制由智利學者Rodriguez等于2004年首次提出并應用于電壓源逆變器[5]。2018年,ABB集團在歐洲率先將模型預測脈沖模式控制應用于大功率工業(yè)電力驅動系統(ACS6080)。這種方法與在20世紀70年代提出的矢量控制相比,在相同的開關頻率下,定子電流總諧波失真(THD)顯著降低[6-7]。結合德國學者德彭布羅克和日本學者高橋在20世紀80年代提出的直接轉矩控制(DTC)的思想,選擇模型預測轉矩控制(MPTC)的控制變量為電磁轉矩和定子磁鏈幅值[8]。在預測階段,基于永磁同步電機的離散數學模型和逆變器產生的離散電壓矢量,預測下一時刻的電磁轉矩和定子磁鏈幅值[9]。在優(yōu)化階段,根據電磁轉矩及定子磁鏈跟蹤誤差最小來設計代價函數,并在下一個采樣時間選擇和應用最優(yōu)電壓矢量,使代價函數最小化[10]。在代價函數中,由于電磁轉矩與定子磁鏈幅值具有不同的量綱,需要添加權重因子以協調兩者之間的權重。然而,相較于線性控制理論的參數分配方法,權重因子的設置缺乏嚴格的理論依據,多采用試錯法與評級法進行。因此,權重因子的設置一直是學術界的研究熱點與難點。近年來,國內外學者主要從標準化代價函數、無權重因子法、排序法等方面展開研究[11-15]。文獻[16]針對感應電機預測轉矩控制,提出定子磁鏈誤差跟蹤項的權重因子為額定轉矩與額定定子磁鏈之比,賦予轉矩跟蹤與磁鏈跟蹤同等的重要性,即標準化代價函數。結果表明,這種配置方法是次優(yōu)方案而不是最優(yōu)方案。文獻[17-18]提出了取消權重因子的控制方案,即以定子磁鏈矢量作為唯一控制變量從而使得代價函數不包含權重因子。文獻[19]在推導電磁轉矩、磁鏈幅值與定子磁鏈矢量之間解析關系的基礎上,提出了永磁同步電機預測磁鏈控制,省略了代價函數中權重因子的設計過程。另一些學者將多目標優(yōu)化理論中的排序方法引入FCS-MPC的“優(yōu)化”階段,同樣不需要權重因子。文獻[20]提出基于分組排序法的感應電機預測轉矩控制,依據轉矩跟蹤誤差和磁鏈跟蹤誤差分別對電壓矢量排序編號,2組序號平均值最小者為最優(yōu)電壓矢量。文獻[21]則提出基于分層排序法的感應電機預測轉矩控制,先選擇使轉矩跟蹤誤差最小的3個矢量,然后再在其中選擇使磁鏈跟蹤誤差最小的矢量作為最優(yōu)電壓矢量。此外,還有一些學者將智能優(yōu)化理論引入模型預測轉矩控制中[22]。文獻[23]利用多目標遺傳算法實現了感應電機模型預測轉矩控制的權重因子優(yōu)化,即電磁轉矩、定子磁鏈和開關頻率的權重因子在離線狀態(tài)下進行了優(yōu)化,然后在實驗中進行了驗證。在文獻[24]中,針對永磁同步電機的模型預測轉矩控制,提出了使用混沌突變的粒子群優(yōu)化的權重因子設計,其中優(yōu)化目標為降低轉矩脈動和定子電流失真。實驗結果表明,該方法能較好地解決權重因子的設置問題,但也增加了系統的復雜度和微處理器的計算負擔。目前,對代價函數權重因子耦合關系的研究多采用仿真方法。文獻[25]針對感應電機模型預測轉矩控制的研究結果表明,不同的權重因子下轉矩的均方根與磁鏈的均方根成反比關系,權重因子過大或過小都會導致系統失穩(wěn)。然而,權重因子的穩(wěn)定邊界值在理論上是無法得到的。文獻[26]以定子電流畸變最小為目標,推導了不同維度的轉矩與磁鏈之間的關系,構建了模型預測電流控制與模型預測轉矩控制之間的關系。
在前人研究的基礎上,本文根據永磁同步電機中電磁轉矩、定子磁鏈和定子電流之間的內在關系,推導代價函數中權重因子的解析表達式。首先闡述模型預測電流控制、模型預測轉矩控制和模型預測磁鏈控制的基本原理;然后描述權重因子解析表達式的推導過程,分析參數失配的影響機制,并對所提出算法進行實驗驗證。
1 數學模型建立與代價函數設計
1.1 永磁同步電機的數學模型與預測模型
基于空間矢量理論,三相永磁同步電機的數學模型為
(1)
ψs=Lsis+ψfejθr
(2)
(3)
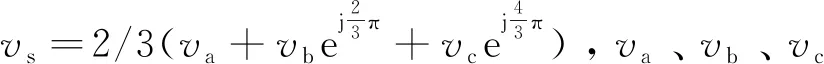
基于一階前向歐拉離散方程
yn+1=yn+Tsf(yn,xn)
(4)
永磁同步電機連續(xù)數學模型(式(1)~式(3))可轉化為離散預測模型,
(5)
ψs(k+1)=ψs(k)+Ts(Rsis(k)+vs(k))
(6)
(7)
式中:p為極對數;Ts為控制周期;is(k+1)、ψs(k+1)、Te(k+1)為k+1時刻的狀態(tài)變量;is(k)、ψs(k)、Te(k)為k時刻的狀態(tài)變量。


圖1 有限集模型預測控制具體框圖
1.2 預測電流控制的代價函數設計
在模型預測電流控制中,代價函數設計為
(8)

預測電流控制是融合了有限集模型預測控制與經典矢量控制思想的控制策略,具有結構簡單、代價函數無需權重因子等優(yōu)點。但是,預測電流控制無法實現電磁轉矩的直接快速調控。同時,由于預測電流控制是一種電壓集的窮舉法,因此在弱磁控制中無法實現電壓外環(huán)反饋控制,目前采用勵磁電流查表法實現弱磁控制[6]。
1.3 預測轉矩控制的代價函數設計
眾所周知,預測轉矩控制是有限集模型預測控制思想與直接轉矩控制相融合的控制策略。預測轉矩控制可以實現電磁轉矩的直接調控,與預測電流控制相比,具有更快的電磁轉矩動態(tài)響應。同時,基于轉子轉速與母線電壓可直接給出定子磁鏈幅值參考值,實現弱磁控制[28]。預測轉矩控制的代價函數通常以電磁轉矩跟蹤誤差與定子磁鏈跟蹤誤差最小為優(yōu)化目標
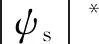
(9)

為了探究不同權重因子下永磁同步電機定子電流總諧波含量、定子磁鏈均方差以及電磁轉矩均方差的變化規(guī)律,進行了MATLAB仿真研究。定子磁鏈均方差及電磁轉矩均方差的計算公式為
(10)
(11)
式中:n為采樣點數,為了提高計算精度,在穩(wěn)態(tài)下,n=3×105;ψs_av、Te_av為采樣點的代數平均值;|ψs|nom、Tnom分別為定子磁鏈、電磁轉矩的額定值。

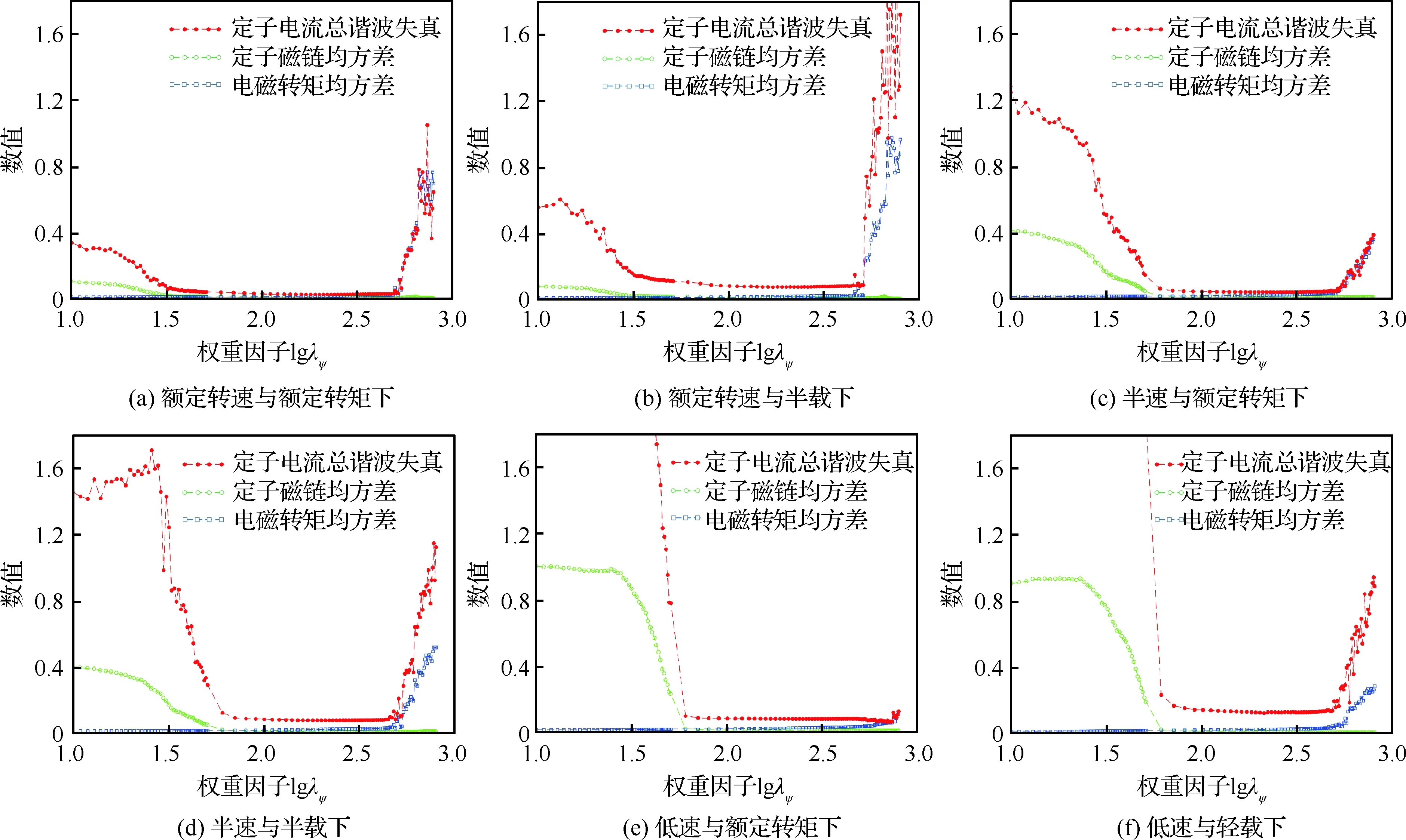
圖2 不同工況不同權重因子下永磁同步電機的定子電流總諧波失真、定子磁鏈均方差與電磁轉矩均方差
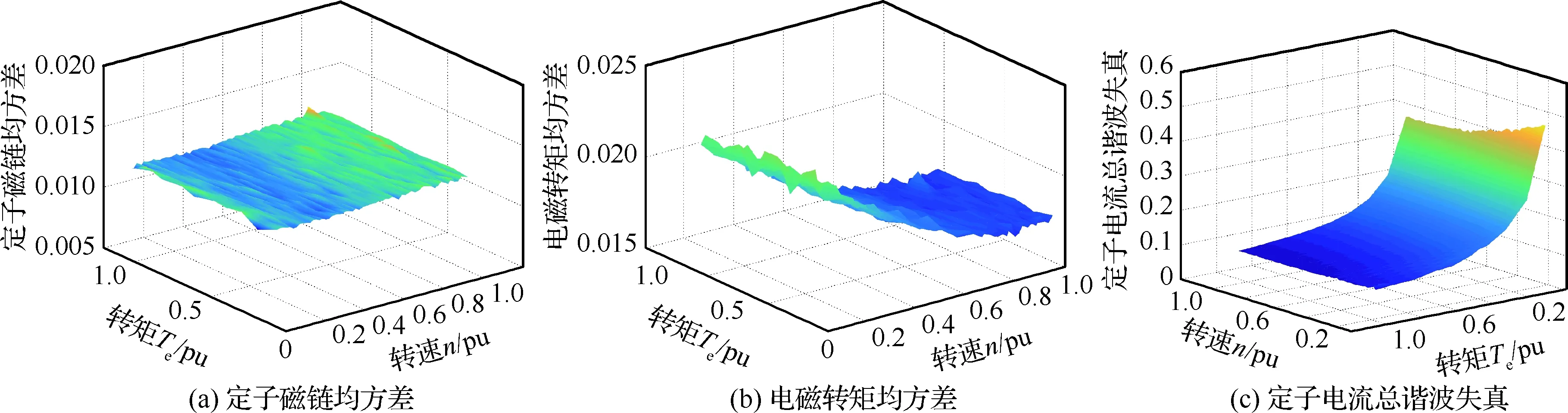
圖3 不同工況與標稱權重因子下永磁同步電機的定子電流總諧波失真、定子磁鏈均方差與電磁轉矩均方差
1.4 預測磁鏈控制的代價函數設計
為保留預測轉矩控制的優(yōu)點,同時克服預測轉矩控制中權重因子設置困難的問題,一些學者提出了模型預測磁鏈控制理論。預測磁鏈控制的代價函數設計公式為
(12)
{cos[θs(k+1)]+jsin[θs(k+1)]}
(13)
θs(k+1)=θr(k)+ωrTs+δsr
(14)
(15)

由式(13)~式(15)可知,預測磁鏈控制以定子磁鏈為控制目標,易于實現弱磁控制,具有快速的動態(tài)響應且不含權重因子。但是,定子磁鏈參考值的計算公式過于復雜,且其中含有電機參數,這降低了控制系統的魯棒性。
1.5 預測磁鏈控制與預測電流控制的關系
預測電流控制的代價函數如式(8)所示,而預測磁鏈控制的代價函數如式(12)所示。已知ψs=Lsis+ψfejθr為定子磁鏈矢量計算的電流模型。因此,進一步簡化代價函數式(12),可得
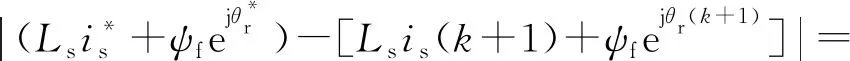
(16)

(17)
由式(17)可知,比較預測磁鏈控制與預測電流控制的代價函數只相差系數Ls。而代價函數的功能是選擇使其最小的電壓作為最優(yōu)電壓,因此兩者在電壓尋優(yōu)方面是等價的。
2 基于新型權重因子解析法的模型預測轉矩控制
2.1 權重因子的解析算法
在永磁同步電機的有限集模型預測控制中,以定子電流跟蹤誤差最小為優(yōu)化目標的代價函數可以表示為
(18)
1.5節(jié)已詳細闡述過2個代價函數式(8)、式(12)在電壓尋優(yōu)方面的等價性,因此根據ψs=Lsis+ψfejθr,該代價函數式(18)可以轉化為以定子磁鏈跟蹤誤差最小為優(yōu)化目標。
已知永磁同步電機的電磁轉矩計算公式可被表示為Te=3p|ψf||ψs|sinδsr/2Ls。因此,式(18)可以進一步等價于


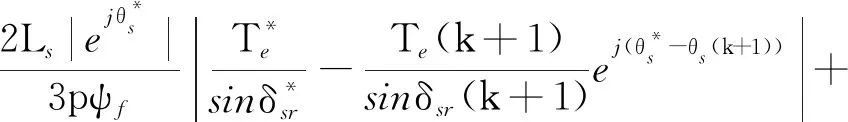

(19)
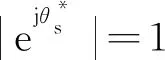
(20)
可以看出,該代價函數式(20)以電磁轉矩和定子磁鏈為優(yōu)化目標,等價于式(18)。
根據上述分析,將式(20)適當變形,可以得到基于解析權重因子的預測轉矩控制代價函數
(21)
式中:λAWF為權重因子。由式(15)可知角度δsr(k+1)隨著電磁轉矩的變化而變化,而λAWF中含有角度δsr(k+1)信息,因此λAWF隨電磁轉矩的變化而變化。
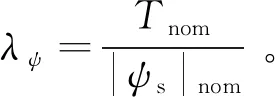

圖4 AWF-MPTC和T-MPTC的定子電流總諧波失真、定子磁鏈均方差和電磁轉矩均方差
2.2 電機參數對權重因子解析算法的影響機制

2.3 參數在線辨識

1.45×10-2
(22)
在永磁同步電機同步旋轉d-q坐標系中,永磁同步電機的q軸定子電流方程為
(23)
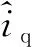
(24)
根據波波夫超穩(wěn)定性理論,系統的穩(wěn)定條件為
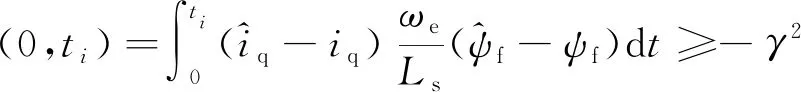
(25)

圖5 參數匹配及參數失配下的AWF-MPTC的定子磁鏈均方差、電磁轉矩均方差和定子電流總諧波失真
式中:γ2為正實數。永磁體磁鏈辨識的自適應律可以表示為
(26)
2.4 算法總體框架


圖6 所提出的AWF-MPTC的總體框圖
3 實驗驗證
在圖7中的永磁同步電機實驗平臺上對AWF-MPTC與T-MPTC進行實驗驗證。永磁同步電機的參數設置如下:Rs=2.83 Ω、Ls=14.7 mH、ψf=0.321 Wb、Tnom=13.2 N·m、nnom=1 500 r/min。

圖7 永磁同步電機實驗平臺
AWF-MPTC與T-MPTC的動態(tài)性能如圖8和圖9所示,速度指令設置為2.0 s時500 r/min、4.0 s時1 500 r/min、6.0 s時800 r/min。實驗結果表明,與傳統T-MPTC相比,本文所提出的AWF-MPTC具有較小的轉矩脈動和定子電流THD(總諧波失真)。當轉速為800 r/min時,AWF-MPTC的轉矩脈動為2.0 N·m,而T-MPTC的轉矩脈動為3.0 N·m。當轉速為500 r/min時,AWF-MPTC 的定子電流THD為11.48%,而T-MPTC的定子電流 THD為13.76%。
負載轉矩突變情況下AWF-MPTC的動態(tài)性能如圖10所示。實驗結果表明,在負載轉矩突變的情況下,轉速有略微下降,出現了動態(tài)降落,之后迅速在基準值建立新的平衡。由此表明,AWF-MPTC在突加負載時的動態(tài)性能良好。
T-MPTC和AWF-MPFC的穩(wěn)態(tài)性能如圖11和圖12所示。其中圖11為額定轉矩與額定轉速下AWF-MPTC與T-MPTC的穩(wěn)態(tài)性能對比圖。圖12為PMSM驅動器的控制算法在4.0 s時從T-MPTC切換到AWF-MPTC。可以看出,轉矩脈動從3.5 N·m降低到2.5 N·m,定子電流THD從13.21%降低到11.08%。與T-MPTC相比,AWF-MPTC穩(wěn)態(tài)性能的改善,一方面得益于解析權重因子,另一方面得益于精確的預測模型。

圖8 AWF-MPTC的動態(tài)性能
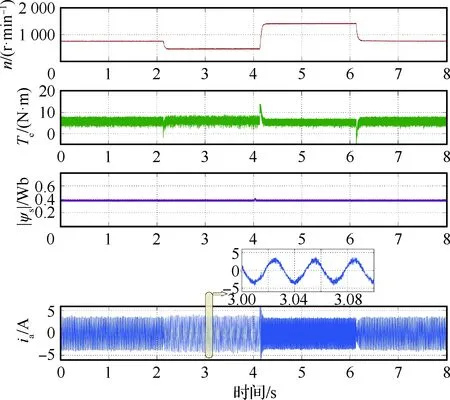
圖9 T-MPTC的動態(tài)性能
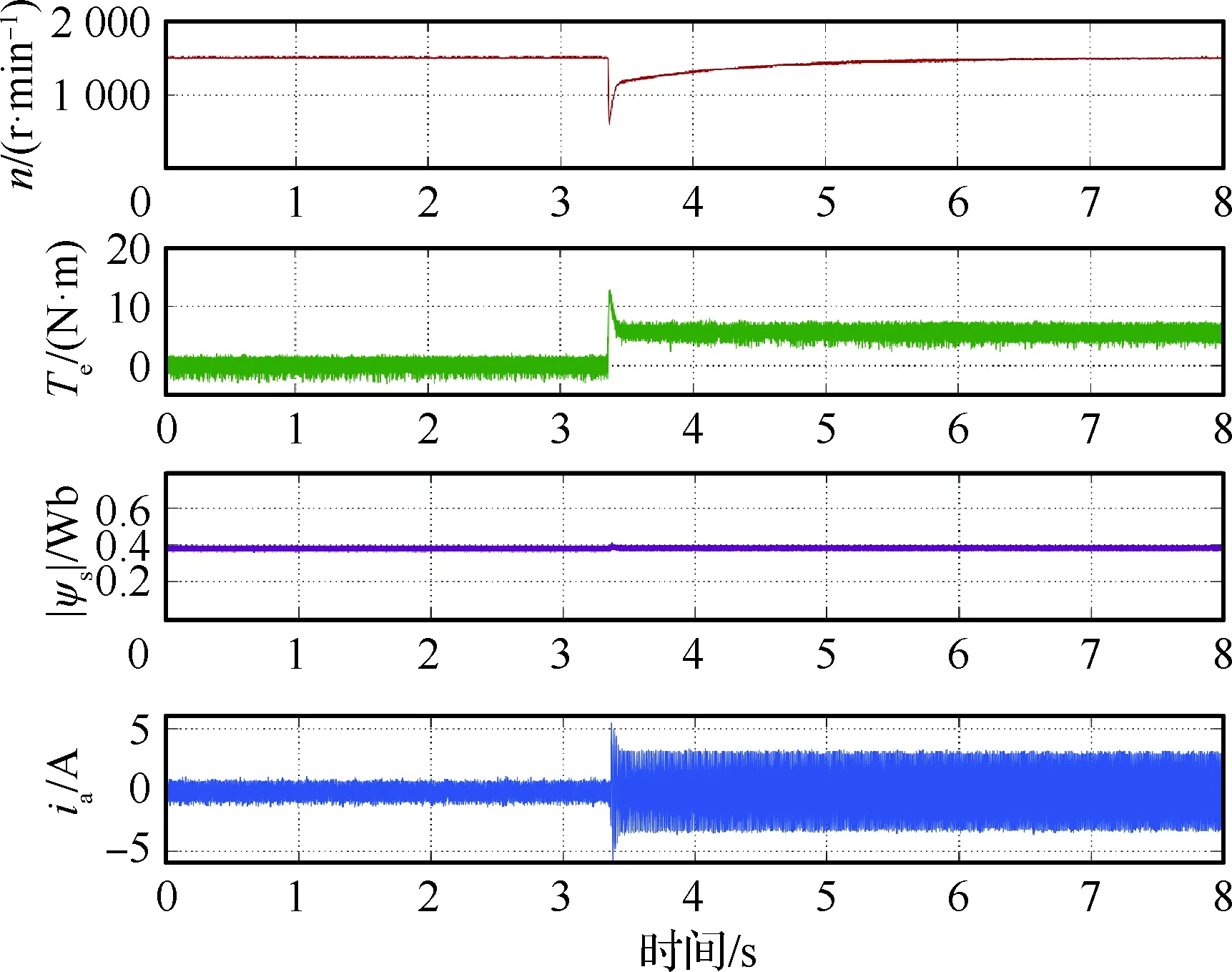
圖10 負載轉矩突變時AWF-MPTC的動態(tài)性能
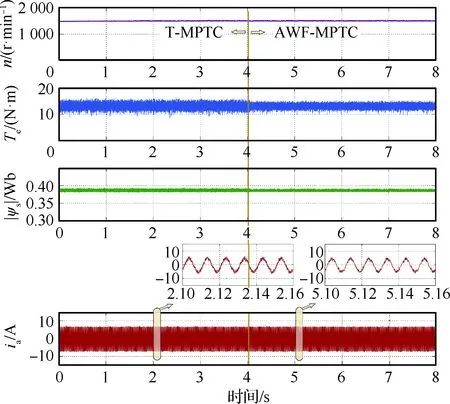
圖11 額定狀態(tài)下T-MPTC和AWF-MPTC的穩(wěn)態(tài)性能
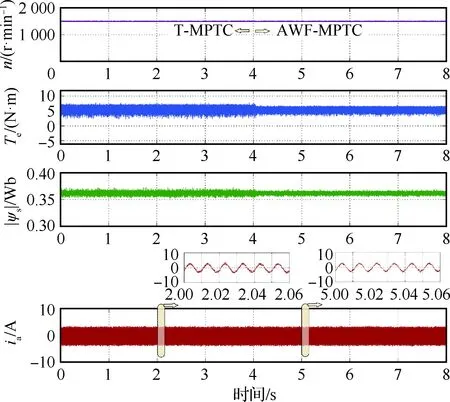
圖12 T-MPTC和AWF-MPTC的穩(wěn)態(tài)性能


圖13 當時T-MPTC、不帶參數辨識AWF-MPTC、AWF-MPTC的魯棒性能

圖14 當時T-MPTC、不帶參數辨識AWF-MPTC、AWF-MPTC的魯棒性能
4 結 論
通過分析永磁同步電機電磁轉矩與定子磁鏈幅值的內在關系,提出了一種永磁同步電機模型預測轉矩控制權重因子的解析計算方法,并仿真對比分析了本文所提出的AWF-MPTC與傳統T-MPTC的定子電流THD、定子磁鏈RMS、電磁轉矩RMS。由于AWF-MPTC的權重因子解析方程依賴于永磁同步電機的參數,因此本文采用在線參數辨識來提高其計算精度和預測模型的精度。實驗結果表明,所提出的AWF-MPTC算法比傳統算法具有更好的動態(tài)性能、穩(wěn)態(tài)性能和魯棒性。但是AWF-MPTC的代價函數不包含開關頻率項及其權重因子,這將是后面要研究的內容。

