基于嵌套網格變幾何軸對稱進氣道非定常數值模擬
羅炯,李志宏,陳科,向歡
航空工業成都飛機設計研究所,成都 610091
隨著飛行器速度不斷提高,未來飛行器飛行范圍得到了極大擴展,速域覆蓋從低速、超聲速到高超聲速,對動力提出了更高的要求,任何單一動力形式都無法滿足從低速到高超聲速的寬速域工作需求,渦輪/沖壓組合動力是最有希望滿足這一需求的動力形式。進氣道作為推進系統的關鍵部件,其性能對飛行器性能有至關重要的影響,必須在寬馬赫數范圍內穩定工作,另外還要求:總壓損失小、出口流場均勻、工作穩定、抗干擾能力強、阻力小等[1]。這就對進氣道寬速域設計提出了巨大挑戰。
如何使進氣道在寬速域范圍內保持良好的工作狀態,一直是組合動力高速飛行器的設計難點,國內外對此開展了很多研究。常用的方法是針對固定幾何進氣道設計抽吸、溢流[2],盡量降低進氣道起動馬赫數,但這種方法效果有限,并不能提高總體性能,甚至可能增加飛行器溢流阻力。此外,更有效的方法是,通過變幾何調節,改善進氣道起動性能,使進氣道能更好地兼顧設計點及非設計點的性能。在各種壓縮形式的變幾何進氣道中,軸對稱進氣道利用中心錐和唇罩內表面對來流進行壓縮,具有壓縮效率高、流場畸變較低等優點,多年來一直受到國內外眾多研究機構和學者的關注,并在高速飛機和導彈上得到了廣泛應用。
20世紀60—70年代,美國針對變幾何軸對稱進氣道進行了深入研究。洛馬公司研制的“黑鳥”SR-71高空高速戰略偵察機(圖1)采用中心錐可前后移動的軸對稱進氣道方案[3],巡航馬赫數可達3.2。美國馬里蘭大學的Colville等就以SR-71軸對稱進氣道為基礎,用CFD的方法研究了多種改變幾何外形的方法及其效果,包括轉動外罩唇角度、中心錐錐角改變等[4-6]。NASA德萊頓飛行研究中心提出了一種在中心錐上開槽(圖2)的方法來拓寬軸對稱進氣道工作范圍[7],在非設計點狀態時,中心錐上的槽道打開,增加喉道的面積,適應低速流量需要,并用F-15飛機掛載進行了進氣道飛行驗證。日本ISAS的研究人員為串聯TBCC發動機ATREX設計了變幾何軸對稱進氣道,在法國ONERA的超聲速風洞完成了變幾何自動調節試驗[8]。東京大學的Kobayashi等還發明了一種中心體由一個頂錐和多個圓盤組成的的多級盤式軸對稱進氣道[9],進氣道中心錐上圓錐盤之間的距離的改變使得中心錐長度隨之改變,從而控制進氣道的流量系數和總壓恢復系數。國內南京航空航天大學對于變幾何進氣道研究也有較多進展,滕建等設計了一種中心錐帶凹腔的變幾何軸對稱進氣道,后退圓錐頭部可提高流量系數[10];李建用設計點馬赫數6.0的軸對稱進氣道數值模擬發現,中心錐向前移動時,不但可以提高低馬赫數下氣動性能,還可以改善起動性能[11]。

圖1 黑鳥SR-71飛機

圖2 中心錐變體進氣道
真實飛行過程中,在進氣道幾何調節和來流擾動的共同影響下,進氣道流場具有強烈的非定常特征,而這種非定常流動極容易造成進氣道的不起動。Wagner等在風洞試驗中采用轉動進氣道出口斜板的方式實現出口反壓的變化,分析了反壓變化引起的進氣道不起動的流場結構[12]。國防科技大學的游進通過數值模擬和試驗相結合的方法對混壓式進氣道再起動特性及調節方法的機理和相關影響因素進行了研究[13]。南京航空航天大學的劉凱禮等對迎角動態變化的二元進氣道進行了非定常數值模擬,進氣道特性有明顯遲滯現象,低速區非定常效應影響顯著[14];王衛星等采用非定常數值方法研究了高超聲速進氣道自起動過程中非定常流動特性,分析了流道外形及來流對進氣道自起動過程中流動特性影響[15]。
目前對于進氣道數值模特的研究一般采用傳統的定常模擬方法,向歡等采用嵌套網格非定常方法對戰斗機大迎角時進氣道氣動特性進行了數值模擬[16],該文中進氣道外形不變,而進氣道變幾何調節過程涉及到進氣道外形的變化,非定常數值模擬研究有待進一步加強。
本文對可調軸對稱進氣道,使用嵌套網格技術數值模擬中心錐前后動態調節非定常過程,同時在調節過程改變來流條件和進氣道出口反壓條件,討論了中心錐動態調節過程中流場變化規律和進氣道性能變化規律,研究了軸對稱進氣道調節的非定常過程在臨界反壓下中心錐移動速度對進氣道起動性能的影響,為進氣道方案設計和改進提供參考。
1 物理模型及計算方法
設計點馬赫數為3.5的單級軸對稱混壓式進氣道的二維模型圖如圖3所示。它由一個軸對稱的中心錐和外罩組成,其半錐角角度為13.5°,內收縮比為2.60。當來流馬赫數發生變化,中心錐體也會相應地前后移動。計算馬赫數為2.5~3.5,飛行高度11 km,攻角0°。不同馬赫數Ma之間的中心體移動規律如圖4所示。從馬赫數2.5~3.5,中心錐一共后移400 mm。錐面激波不斷后退,激波角不斷減小。在每個馬赫數變化的區間內,假定中心錐的位移隨馬赫數線性變化。
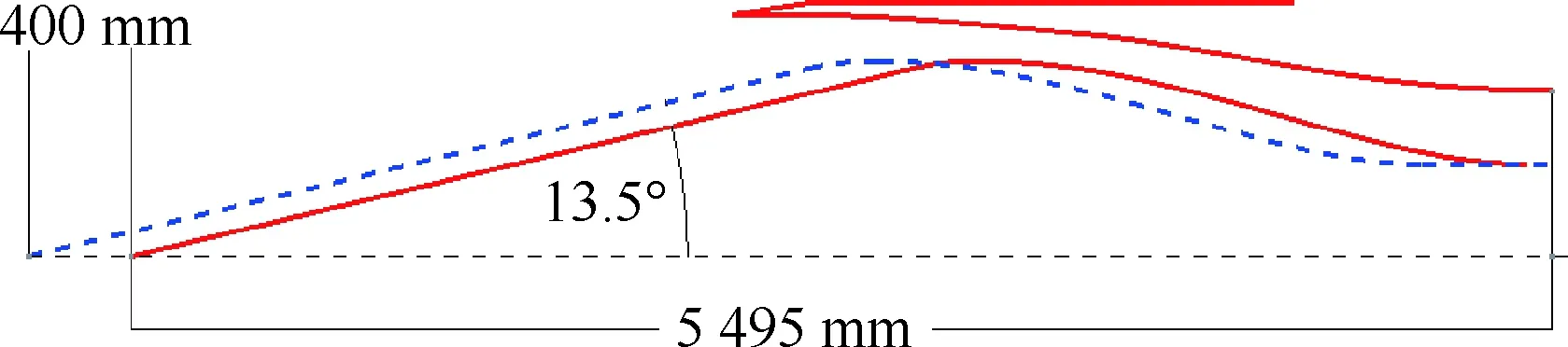
圖3 軸對稱進氣道方案
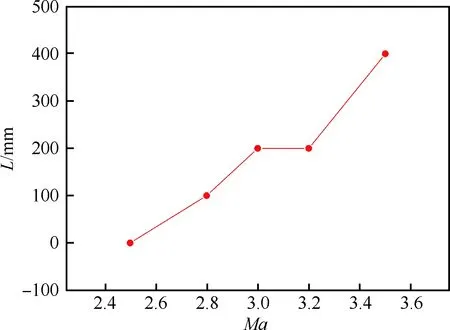
圖4 中心錐移動變化規律
本文所用計算軟件是Metacomp Technologies公司的CFD++,該軟件基于有限體積法求解RANS方程,軟件可計算結構化或非結構化網格,擁有MPI并行計算能力,其中無黏項是2階TVD格式,黏性項采用中心離散格式,湍流模型采用Realizablek-ε模型。對于定常狀態,初始流場為來流條件,此時整個流場的流動參數都和來流一樣。當出口流量不再變化時,認為得到穩態結果。非定常計算采用URANS方法,初始流場為初始時間的穩態流場,采用隱式LU-SGS時間推進方法,通過引入子迭代即雙時間步使得時間方向上達到較高的精度,總時間步設置為0.5 ms,其中子迭代設置10步即可讓子迭代內殘差能夠下降3個數量級。嵌套過程如圖5~圖8所示,其中背景網格數為16萬,嵌套網格數為3萬。嵌套網格會把背景網格中多余的部分切割下來,得到我們想要的完整網格。進氣道模型生成的非結構網格如圖7所示。網格總數為5萬,物面第1層網格厚度為0.012 mm。進氣道內部網格適當加密,以便能解析更真實流動狀態。遠場邊界為3.0 m,避免計算過程激波的影響。在模擬中心錐的移動時,使用了CFD++中嵌套網格技術。將中心錐用網格包裹,嵌套入背景網格之中,當中心錐移動時,包裹中心錐的嵌套網格整體移動即可。
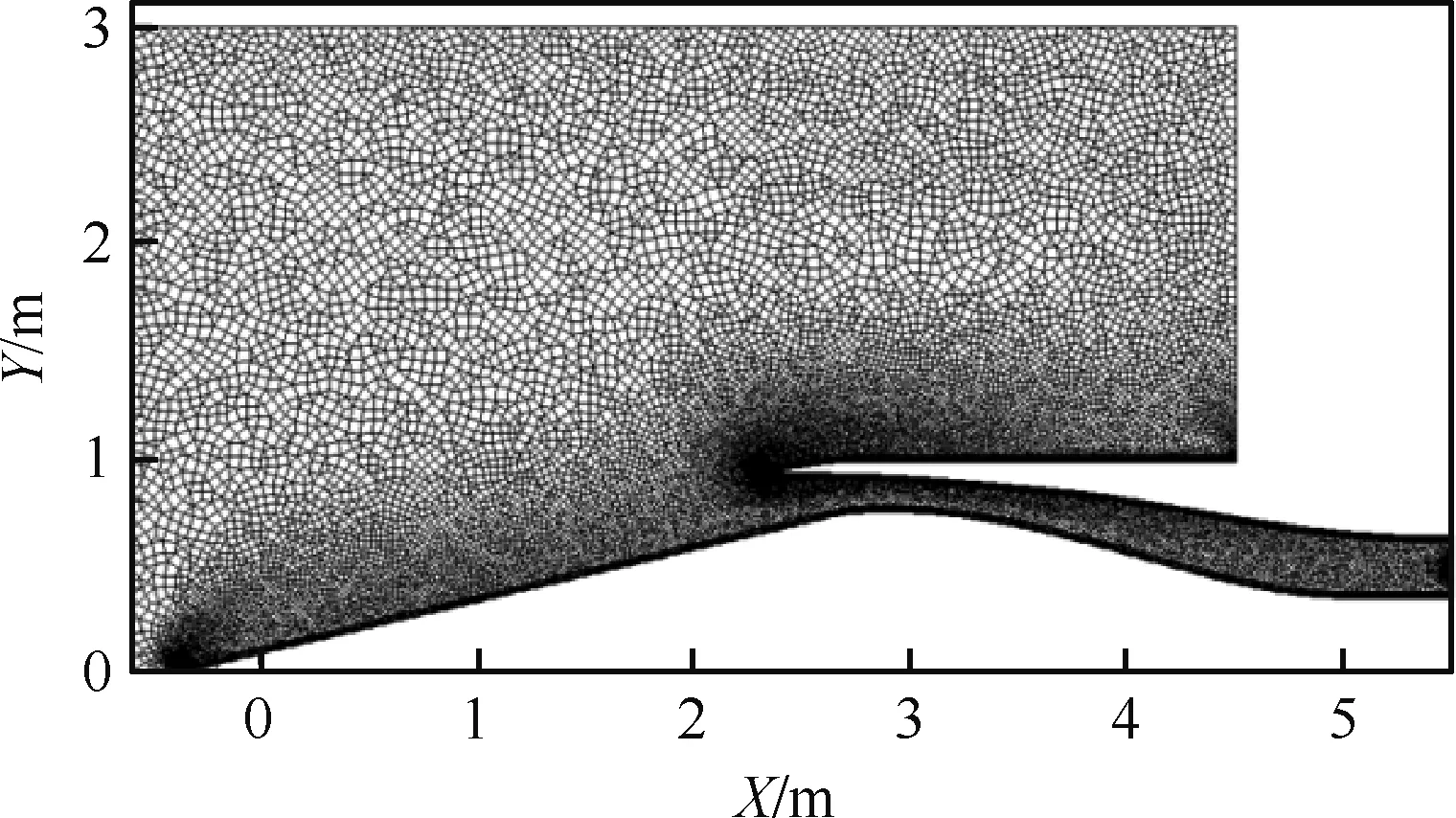
圖5 定常計算網格

圖6 背景網格

圖7 嵌套網格
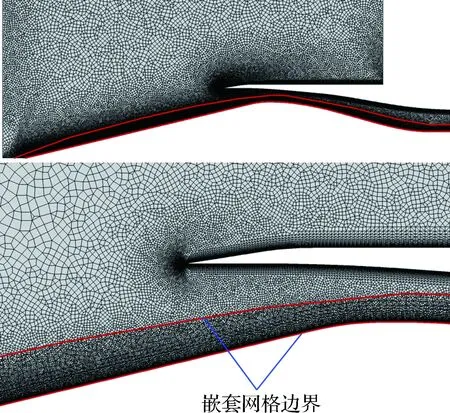
圖8 非定常計算網格
本文先對典型馬赫數工況進行了定常模擬,通過逐步增加反壓,研究了典型馬赫數下進氣道的抗反壓能力。然后對進氣道動態調節過程進行了非定常模擬,研究了進氣道動態調節時的流場變化規律。
2 定常狀態計算分析
圖9給出了設計狀態Ma=3.5在不同進氣道出口反壓Pb下馬赫數分布和密度梯度的模分布云圖,其中密度梯度的模清晰地反映了流場的激波結構。正激波被推出之前,錐面激波基本封住了唇口,流量系數接近100%,隨著不斷增加出口反壓,正激波最終被推出。表1給出了流量系數和總壓恢復系數隨反壓的變化情況,定常狀態計算下,進氣道出口反壓增大到43.5P∞(P∞為遠場來流壓力)時進氣道仍然處于起動狀態,超過此反壓進氣道將不起動,此時進氣道處于臨界狀態。進氣道進入不起動狀態后,進氣道出口的流量系數和總壓系數均出現大幅降低。反壓較小時,結尾激波處在進氣道喉道后的擴張段,此時結尾激波前馬赫數較高,總壓損失較大;隨著反壓增大,結尾激波移動到喉道處,波前馬赫數降低,結尾激波損失較小,進氣道總壓恢復系數得到提高。
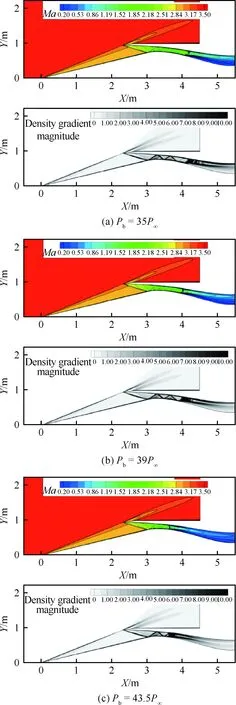
圖9 Ma=3.5不同反壓下進氣道出口流場結構
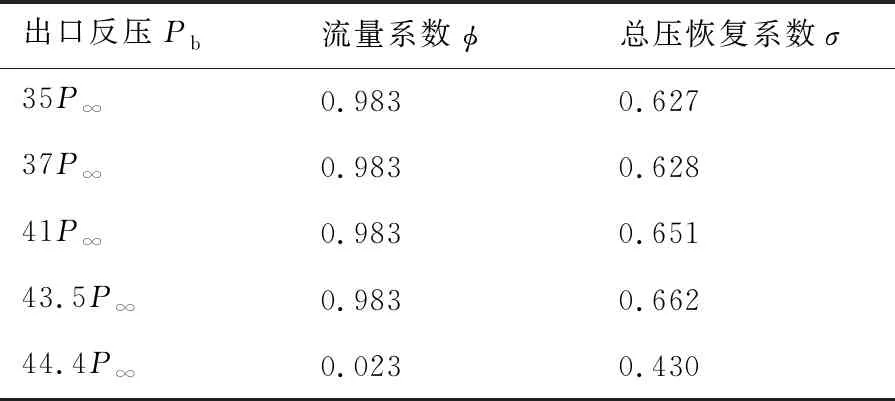
表1 Ma=3.5時進氣道性能
圖10給出了Ma=2.5~3.2工作狀態進氣道馬赫數分布和密度梯度的模分布云圖。隨著馬赫數的增加,第1道斜激波不斷增強,氣流進入進氣道后經過多道斜激波增壓減速,在進氣道喉道后形成一道末激波將氣流減速到亞聲速。表2給出了各個馬赫數的起動狀態進氣道工作狀態時進氣道出口反壓、流量系數和總壓恢復系數。隨著馬赫數增加,中心錐不斷后移,錐面斜激波角減小,到設計狀態馬赫數3.5形成封口,流量系數也隨之增加。由于馬赫數3.0~3.2中心錐沒有移動,故馬赫數3.2下總壓恢復系數偏小,馬赫數3.2~3.5中心錐向后移動了200 mm,內收縮比增大,大幅改善了設計點馬赫數3.5總壓恢復系數。
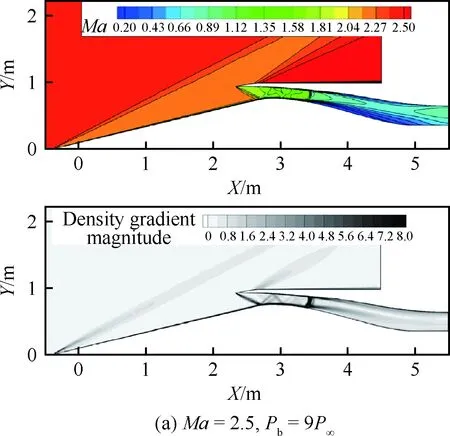
圖10 Ma=2.5~3.2工作范圍進氣道流場
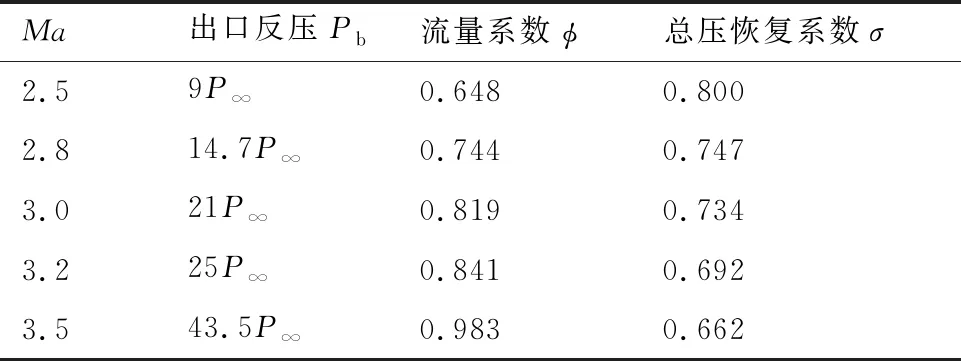
表2 不同來流調節進氣道性能
3 非定常狀態計算分析
根據進氣道的設計,當馬赫數從2.5增加到2.8,中心錐后移D=100 mm,進氣道出口反壓會從9P∞增加到14.7P∞,圖11~圖12給出了計算來流馬赫數隨時間變化及出口反壓隨時間變化,兩者均為線性變化,通過非定常方法數值模擬此動態過程。分別用1 s總時間來實現這一過程,研究非定常的流場變化情況。初始時刻t=0 s時流場為Ma=2.5時定常計算得到的穩態流場。
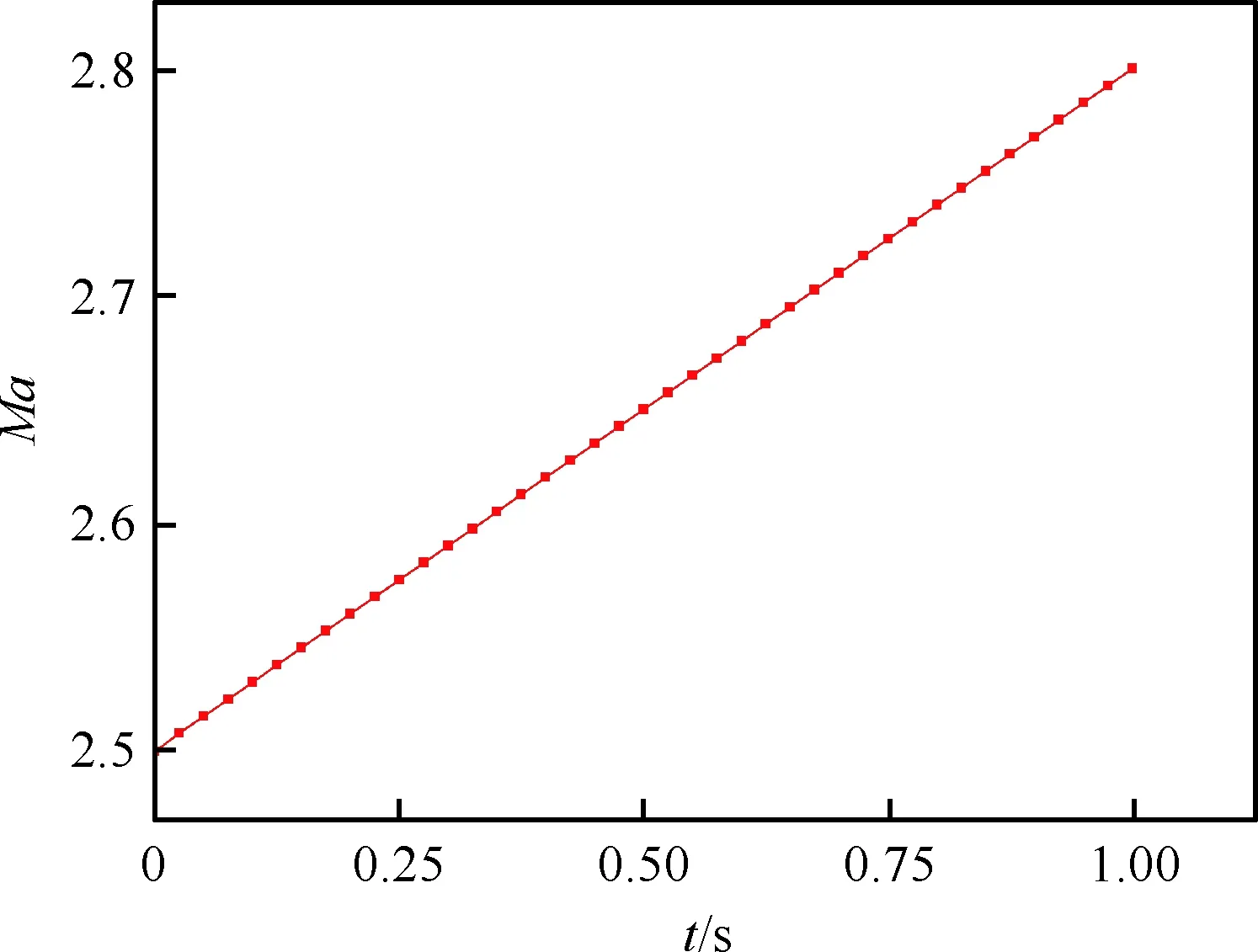
圖11 來流馬赫數隨時間變化
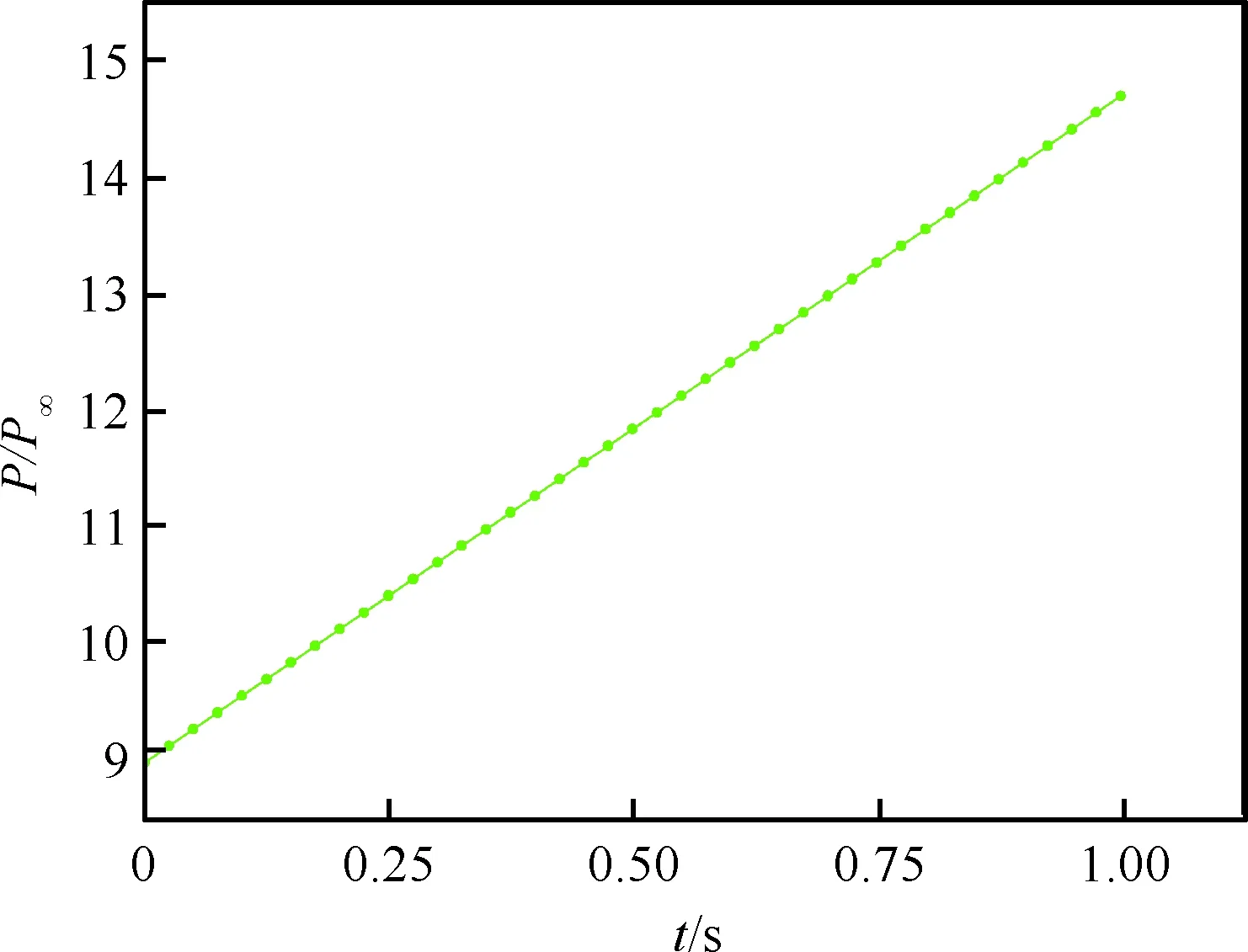
圖12 進氣道出口反壓隨時間變化
圖13給出非定常計算結果各個時刻的馬赫數云圖分布,圖14給出了非定常計算各個時刻流場激波結構變化情況。中心錐移動過程中,來流馬赫數不斷增加,錐面激波逐漸向唇口移動,唇口反射激波不斷增強,唇口到喉道處形成了激波串,將流體進一步增壓減速,結尾激波保持在喉道附近,進氣道保持起動狀態。圖15~圖16給出了進氣道流量系數及總壓恢復系數隨時間變化規律,流量系數基本隨時間線性增加,總壓恢復系數基本隨時間線性減小。表3給出了計算結束時刻進氣道出口流量系數和總壓恢復系數與定常狀態對比,相比于定常狀態,非定常計算結果得到的流量系數降低了0.019,總壓恢復系數降低了0.015。
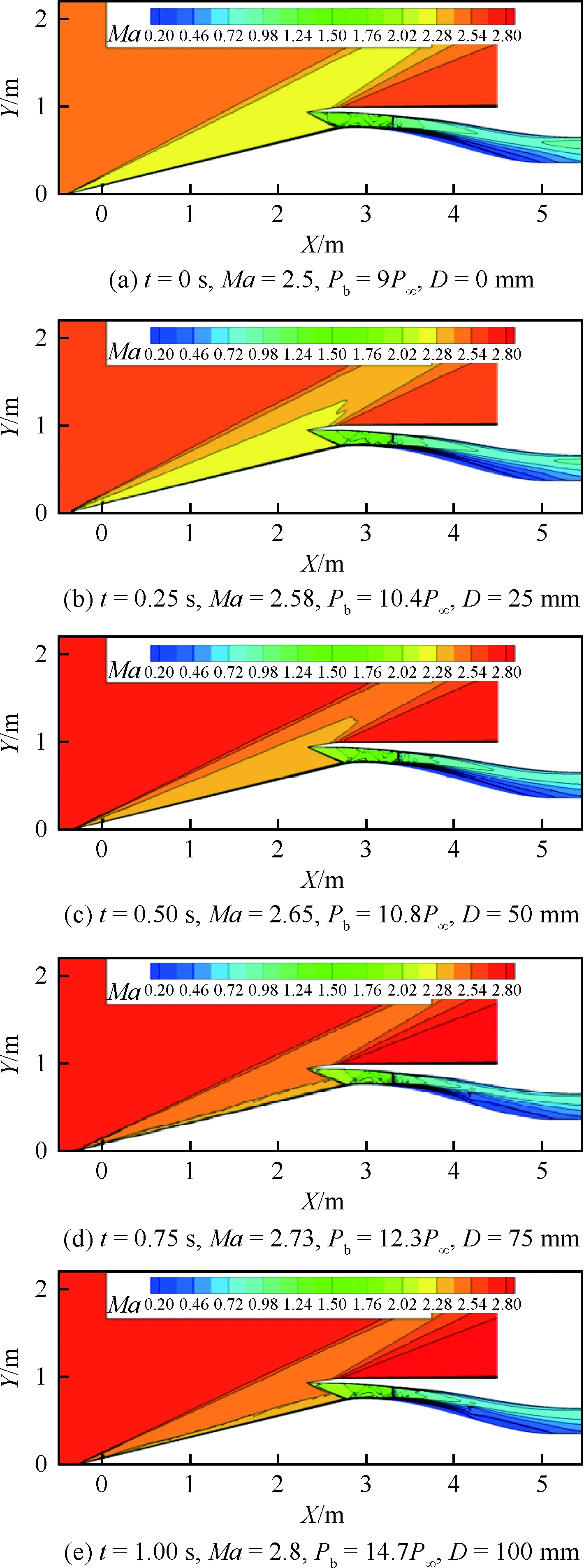
圖13 不同時刻馬赫數云圖分布(Ma=2.5~2.8)
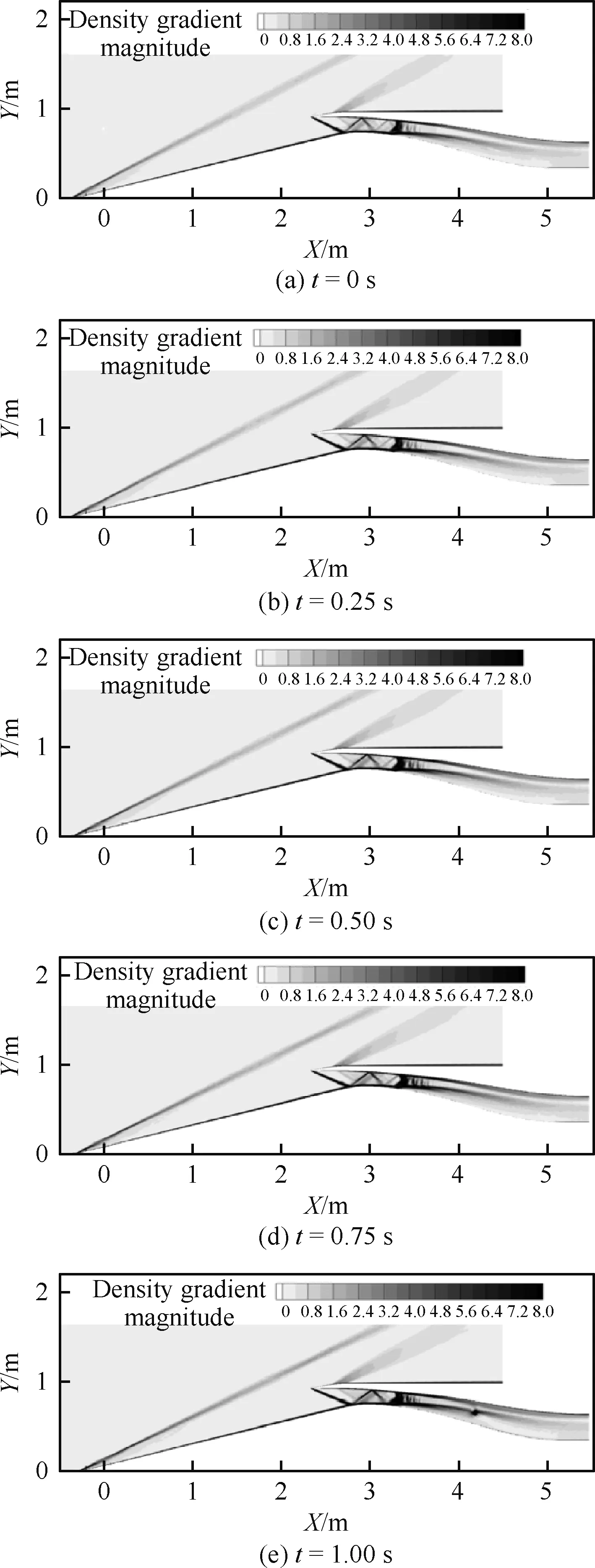
圖14 不同時刻流場激波結構(Ma=2.5~2.8)
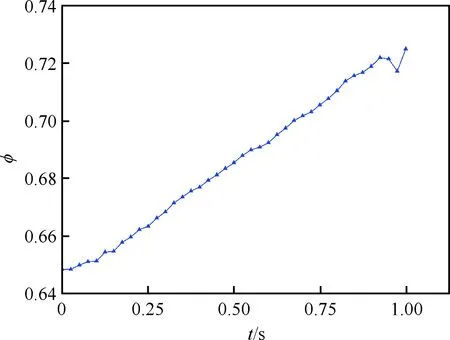
圖15 進氣道流量系數隨時間變化
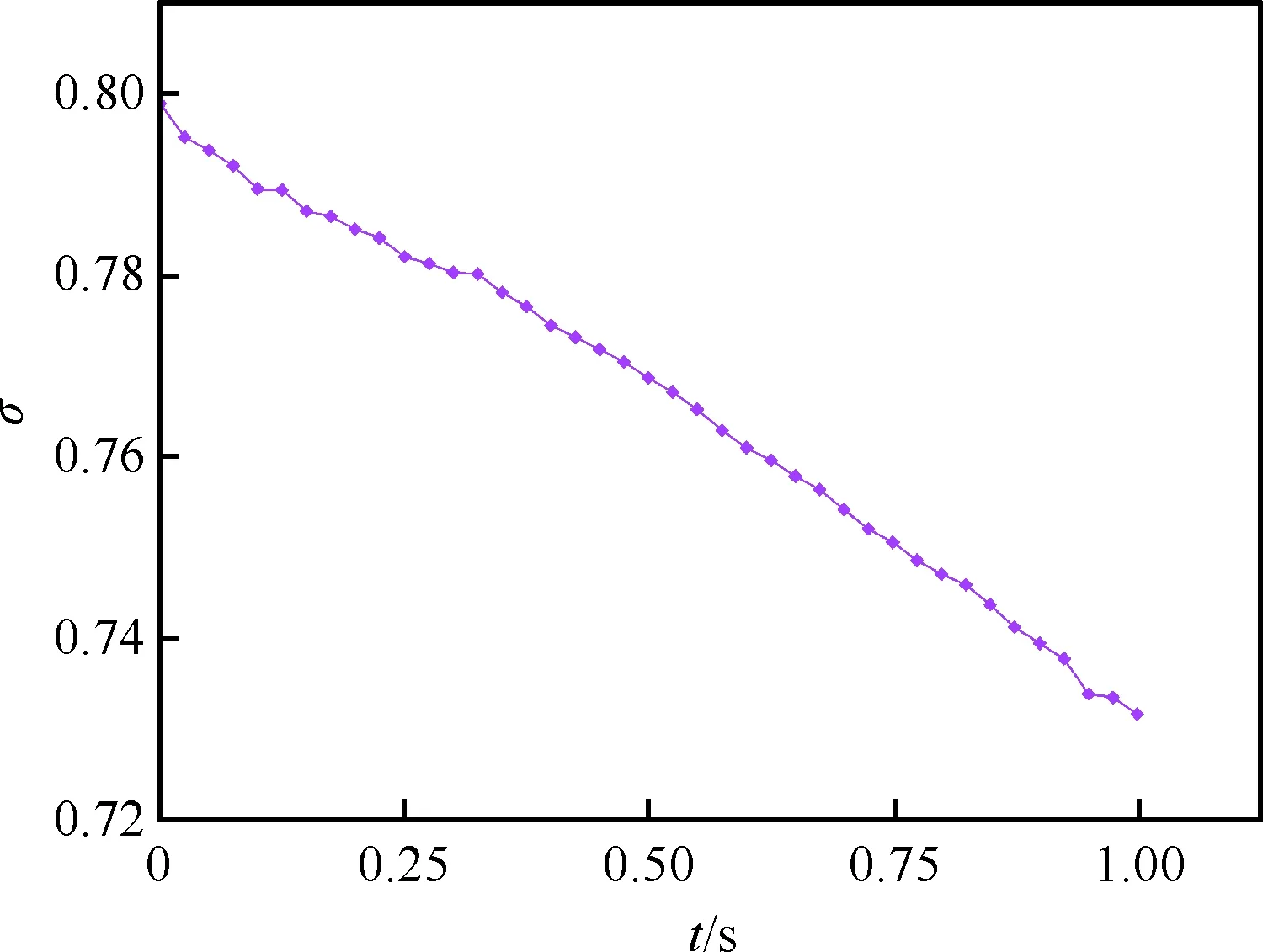
圖16 進氣道總壓恢復系數隨時間變化

表3 動態調節時進氣道性能變化(Ma=2.8)
考慮中心錐不移動,來流條件從馬赫數3.0增加到3.2,進氣道出口反壓從21P∞增加到25P∞,假定來流馬赫數和反壓隨時間線性增加,通過非定常方法數值模擬此動態過程。整個過程耗時1 s,初始時刻t=0 s流場為Ma=3.0時定常計算得到穩態流場。圖17給出了非定常計算得到馬赫數云圖分布在各個時刻變化,隨著來流馬赫數增大,錐面激波逐漸靠近唇口,唇口激波前馬赫數不斷增大,唇口激波強度增加,結尾激波小幅向后移動,基本保持在喉道附近,進氣道處于起動狀態。表4給出了馬赫數為3.2時,定常狀態和非定常狀態計算得到進氣道性能,流量系數變化不大而總壓恢復系數下降0.01。
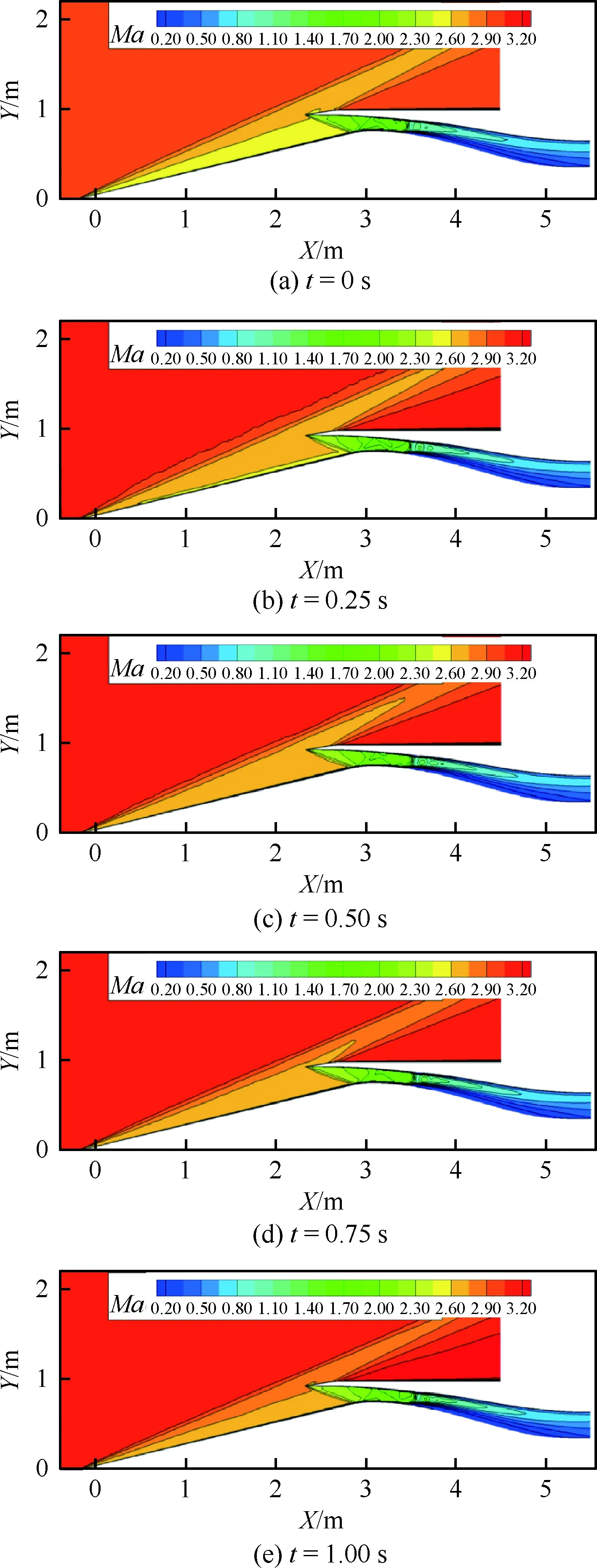
圖17 不同時刻馬赫數云圖分布(Ma=3.0~3.2)

表4 動態調節時進氣道性能變化(Ma=3.2)
4 結 論
通過CFD數值模擬分析了某款混壓式軸對稱進氣道在典型工況的抗反壓能力和設計點基本性能,之后又通過非定常方法模擬了進氣道在典型工況點間動態調節的過程中流場變化和進氣道性能變化規律,得到了以下結論:
1) 在同一來流馬赫數下,隨著進氣道出口反壓的提高,進氣道內結尾激波向喉道移動,波前馬赫數降低,激波損失減小,總壓恢復系數得到提高,當進氣道出口反壓超過一定值后,結尾激波被推出進氣道內,整個進氣道處于不起動狀態。
2) 非定常數值模擬中心錐移動過程,在馬赫數2.5~2.8過程中,中心錐向后移動了100 mm,錐面激波逐漸向唇口靠近,唇口激波逐漸增強,結尾激波基本保持在喉道附近,進氣道處于起動狀態。
3) 非定常計算和定常計算結果對比可知,進氣道受到動態過程小擾動影響性能略微下降。

