分布參數不確定性重要性分析的高效求積公式法

劉俊超,李璐祎

(西北工業大學 航空學院,陜西 西安 710072)

在工程實際中,由于生產水平、加工工藝等因素的制約,結構系統的材料特性、結構尺寸和制造誤差等變量中廣泛地存在多種不確定性[1]。一般按照不確定性的來源可將其分為2類:客觀的不確定性和主觀的不確定性。客觀的不確定性與變量內在的固有隨機性有關,是不可縮減的固有屬性,而主觀的不確定性與不完善的信息及有限的數據有關,可隨著認知的深入和數據的豐富而減小[2]。

靈敏度分析常常用來衡量模型輸入不確定性對模型輸出不確定性的貢獻程度[3]。靈敏度分析分為局部靈敏度分析和全局靈敏度分析。其中,全局靈敏度分析又被稱為重要性測度分析,用來衡量變量在其整個不確定性范圍內變化時對輸出性能統計特征的貢獻程度[4]。目前國內外學者們對輸入變量的重要性測度分析方法做了大量的研究,比如Saltelli[5]提出了基于非參數的方法,Sobol[6]提出了基于方差的重要性分析方法,Borgonovo[7]提出了矩獨立分析方法。由于基于方差的重要性測度分析方法具有模型獨立、重要性測度與輸入-輸出關系一一對應等良好的特性,是目前國際上最常使用的方法之一[8]。

上述提到的重要性測度分析方法并沒有考慮輸入變量分布參數的不確定性,但實際上由于認知和測量水平的限制,輸入變量的分布參數并非是確切可知的,因此分布參數具有不確定性的重要性分析方法得到了越來越多的關注[9]。分布參數的不確定性有多種描述方式,常見的有區間模型[10]、模糊集模型[11]以及主觀概率密度函數[12]等。對于存在分布參數不確定性的情況,輸入變量和分布參數的不確定性傳遞過程可定性地描述為:分布參數→輸入變量→輸出變量→輸出性能統計特征。因此分布參數的不確定性會引起輸出性能統計特征的不確定性,這就要求在進行重要性分析時考慮分布參數在其整個變化范圍內對模型輸出性能統計特征的影響。

對于分布參數具有不確定性的模型,本文借助輸入變量基于方差的重要性分析思想,建立了衡量分布參數對輸出統計矩影響的重要性測度指標,并針對直接求解分布參數重要性測度指標需要3層蒙特卡洛(Monte Carlo,MC)抽樣,計算成本過高的問題,提出2種基于代理抽樣概率密度函數(surrogate sampling probability density function,SSPDF)[13]的求積公式(cubature formula,CF)方法來解決此問題。所提分析方法首先將求積公式運用到分布參數不確定性基于方差的重要性測度指標求解過程中,以提高分布參數重要性測度指標中嵌套的期望和方差算子的計算效率;其次,引入代理抽樣概率密度函數方法,以降低輸入變量參數不確定性向輸出性能統計矩傳遞過程中的計算量;最后,將單層蒙特卡洛(quasi-Monte Carlo,QMC)方法[5]與求積公式相結合,以降低重要性測度指標求解過程中嵌套的期望和方差算子的計算量。

1 分布參數基于方差的重要性測度指標

當輸入變量X的分布參數具有不確定性時,輸出的統計特征值也將具有不確定性。衡量輸入變量的單個分布參數或多個分布參數的交互作用對模型輸出統計特征值(這里以均值、方差為例)方差的貢獻程度,可以為改變分布參數以減小模型輸出的不確定度提供依據[14]。

當輸入變量X=(X1,X2,…,XdX)的分布參數Θ具有不確定性時,模型輸出將同時具有主觀不確定和客觀不確定,可表示為

Y=g(X,Θ)

(1)

式中,Θ=(Θ1,Θ2,…,ΘdΘ)是輸入變量X的dΘ維相互獨立的分布參數變量。在本文中,參數的主觀不確定性用主觀概率密度函數fΘ(θ)來描述[12]。當Θ取某一特定值θ(·)時,輸入變量X的不確定性由條件概率密度函數fX(x|θ(·))來衡量。

當輸入變量X的分布參數Θ具有不確定性時,輸出的均值和方差不再只受到輸入變量X的不確定性影響,而是可以描述為分布參數Θ的函數

因此,類似于輸入變量的基于方差的重要性測度的定義,分布參數Θ分別對Μ和D的主重要性測度和總重要性測度如(4)～(5)式和(6)～(7)式所示

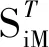
2 分布參數基于方差的重要性測度指標求解的高效方法

從(4)～(7)式可以看出,求解參數的重要性測度指標的關鍵仍在于求解嵌套的期望和方差算子。然而,不同于輸入變量基于方差的重要性測度指標,參數的重要性測度指標求解過程需要將參數的不確定性傳遞到輸出均值和方差,是一個分布參數Θ和輸入變量X嵌套的雙層抽樣過程。如果利用抽樣方法求解(4)～(7)式中指標,則整個過程是一個“3層嵌套”的抽樣過程,計算量太大難以為工程實際所接受[15]。求積公式利用少量的積分點和權重便能計算輸出的均值和方差,并且對更高維度的輸入仍有良好的適用性與精確度[16]。Li等[13]提出的代理抽樣概率密度函數方法可以將參數不確定性向輸出均值和方差傳遞過程中的雙層抽樣簡化為單層,在很大程度上提高了參數不確定性傳遞的效率。因此,本文將CF和SSPDF引入到參數的重要性分析中,首先提出了參數重要性測度指標求解的S-DLCF算法,然后再結合QMC方法,提出了S-SLCF算法。

2.1 求積公式

對于一個模型Z=φ(Θ)(Z可以是(2)式中的均值M或(3)式中的方差D),由于CF估計統計矩是在標準正態空間中進行的[17],因此首先通過Rosenblatt變換或Nataf變換將該模型轉化為獨立標準正態變量λ=(λ1,λ2,…,λdΘ)的一個函數[18]

Z=φ(Θ)=φ(R-1(λ))=ρ(λ)

(8)

式中，R-1(·)表示Rosenblatt變換或Nataf變換；ρ(λ)表示獨立標準正態變量λ的多元函數。

因此,根據(8)式,Z的一階和二階中心距,也即Z的期望和方差,可以表示為

式中,fλ(λ)表示獨立標準正態變量λ的聯合概率密度函數。

根據求積公式的理論,(9)～(10)式中的積分可利用少量合適的積分點和相應的積分權重高效地計算得出,可以表示為[19]

式中,N是求積權重ωj與相應的積分點λj的數目。

Xu等[18]已經證明了CF能夠精確估計大多數問題中函數的一階矩和二階矩。表1～2中列出了目前已知的最有效的5類求積公式,從其中可以看出,CF所需的積分點個數與變量維數有關且呈二次增長關系。

表1 公式Ⅰ～Ⅳ的積分點個數[18]

表2 公式Ⅴ中的積分點個數[18]

對于中低等維度變量,積分點的個數只有幾十個或幾百個,體現出了高效性[19]。公式Ⅰ、Ⅱ和Ⅴ受限于變量維度,公式Ⅳ的計算誤差隨變量維數的增加而增加,公式Ⅲ的計算誤差相比較而言更加穩定[16]。

因此,本文選擇公式Ⅲ計算嵌套的期望和方差,其表示形式為

(13)

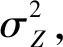
2.2 代理抽樣概率密度函數方法

2.1節中的求積公式方法可以高效地求解(4)～(7)式中嵌套的期望和方差算子。然而,在求解過程中首先需要將參數Θ的不確定性傳遞到輸出的均值和方差,該過程需要雙層嵌套的輸入變量X和參數Θ抽樣。為解決計算成本昂貴的問題，Li等[13]提出了代理抽樣概率密度函數方法。

考慮(8)式中的輸出均值模型,通過引入SSPDFhX(x|θ*),可將輸出均值M表示為

(14)

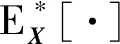
根據方差的計算式V(Y)=E(Y2)-E2(Y),(9)式中的輸出方差模型引入SSPDFhX(x|θ*)后,可將輸出方差D表示為

(15)

由(14)～(15)式可知,當在輸出均值和方差函數的計算過程中引入SSPDFhX(x|θ*)時,輸入變量X是由含有確定參數θ*的SSPDFhX(x|θ*)產生,不依賴于真實的分布參數。因此,在計算M和D時,分布參數Θ在外層變化,內層所產生的輸入變量X的樣本可重復使用。

采用(14)～(15)式計算M和D時,SSPDFhX(x|θ*)的選取是關鍵。文獻[13]指出,當輸入變量X隨其具有不確定性的分布參數Θ改變時,hX(x|θ*)應該覆蓋輸入變量X的整個變化范圍。一種簡單而直接的方法是,根據分布參數Θ的變化范圍確定相應的輸入變量X的極限分布,然后根據輸入變量X的極限分布確定SSPDFhX(x|θ*)。具體的選取方法可參考文獻[13]。

2.3 基于代理抽樣概率密度函數的雙層求積公式(S-DLCF)算法

將(2)～(3)式中的輸出期望和方差模型統一表示為2.1節提到的Z=φ(Θ),參數Θ的不確定性可以通過2.2節的代理抽樣概率密度方法傳遞到輸出Z。從(4)～(7)式可以看出,求解重要性測度指標的關鍵是計算分布參數對Z方差的貢獻VΘi[EΘ～i(Z|Θi)]和VΘ～i[EΘi(Z|Θ～i)],而這些方差貢獻均是期望和方差算子的嵌套。由于該算法的雙層嵌套過程較長,將其分為兩部分進行描述。

首先,求解SiZ,也即通過S-DLCF求解分布參數Θi對Z的主重要性測度,其基本步驟如下所示[19]

1) 估計無條件期望E(Z)和方差V(Z)

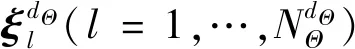
②根據2.2節方法確定SSPDFhX(x|θ*),并由hX(x|θ*)抽取輸入變量X的NX個樣本xk(k=1,…,NX),進而求得相應的模型輸出Y。

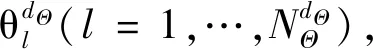
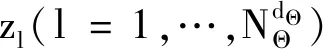
2) 估計EΘ～i(Z|Θi)和VΘi[EΘ～i(Z|Θi)]

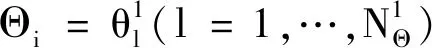
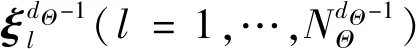
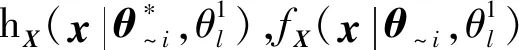
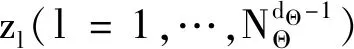
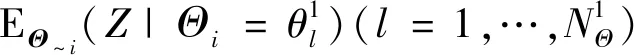
3) 將求得的V(Z)和VΘi[EΘ～i(Z|Θi)]代入(4)或(5)式中便可得到SiZ。

1) 和求解主重要性測度時的步驟1)相同。

2) 估計VΘi(Z|Θ～i)和EΘ～i[VΘi(Z|Θ～i)]

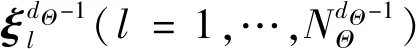
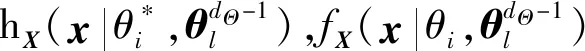
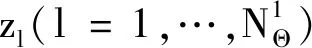
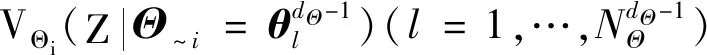
Θ～i)]。

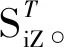
2.4 基于代理抽樣概率密度函數的單層求積公式(S-SLCF)算法

該算法將QMC方法[5]的思想引入到求解嵌套的期望與方差中。對于模型Z=φ(Θ),以方差貢獻VΘi[EΘ～i(Z|Θi)]和VΘ～i[EΘi(Z|Θ～i)]為例,準蒙特卡洛法求解嵌套期望和方差可表示為

(16)

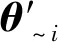
根據(16)式,通過將積分維度從dΘ維擴展到2dΘ-1維,可將(10)式或(11)式中的雙層嵌套積分簡化為單層積分,只需要分別估計期望E[G(Θ)]和無條件期望E(Z)便可得到VΘi[EΘ～i(Z|Θi)],進而可得主重要性測度,這大大簡化了求解過程。

同樣地,求解VΘ～i[EΘi(Z|Θ～i)]可被簡化為

(17)

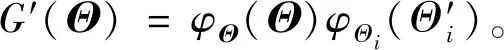
利用S-SLCF方法求解分布參數Θi對Z的主重要性測度和總重要性測度的基本步驟為：

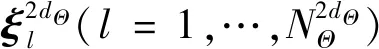
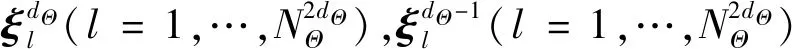
3) 根據2.2節確定相應的SSPDFhX(x|θ*),用hX(x|θ*)抽取輸入變量X的NX個樣本xk(k=1,…,NX),進而求得相應的模型輸出Y。

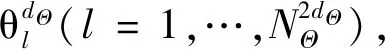
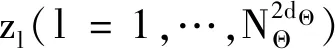
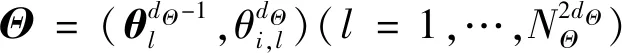
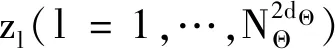
8) 將E[G(Θ)]和E(Z)代入到式(16)中得到VΘi[EΘ～i(Z|Θi)],將該結果及步驟5)中求得的V(Z)代入到(4)式或(5)式中得到SiZ。

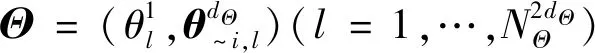
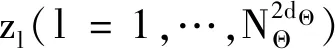
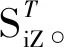
2.5 2種算法的比較

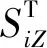
3 算例分析

在本節的算例計算過程中,為了驗證所提方法的效率和精度,以MC方法所得結果作為參考解[20],以QMC方法所得結果作為對比解。在求解分布參數的主重要性測度指標和總重要性測度指標時,MC方法的模型調用次數為dΘ×NΘ×NΘ×NX,QMC方法的模型調用次數為(dΘ+2)×NΘ×NX,其中MC方法中的樣本量統一為NX=NΘ=2 500,QMC方法中的樣本量統一為NX=NΘ=30 000,以保證所求的重要性測度指標收斂。

3.1 可加性非線性模型

根據SSPDF的選取原則,該算例中選取SSPDF為正態分布N(4,22)來抽取輸入變量X的樣本。

2種所提方法計算得到的重要性測度指標如表3所示,eQMC,eS-DLCF,eS-SLCF分別表示各方法相對于MC方法得到的參考解的相對誤差。其中，4種方法的計算量分別為3×(2 500)3,5×(30 000)2,37×1 000,5 000。

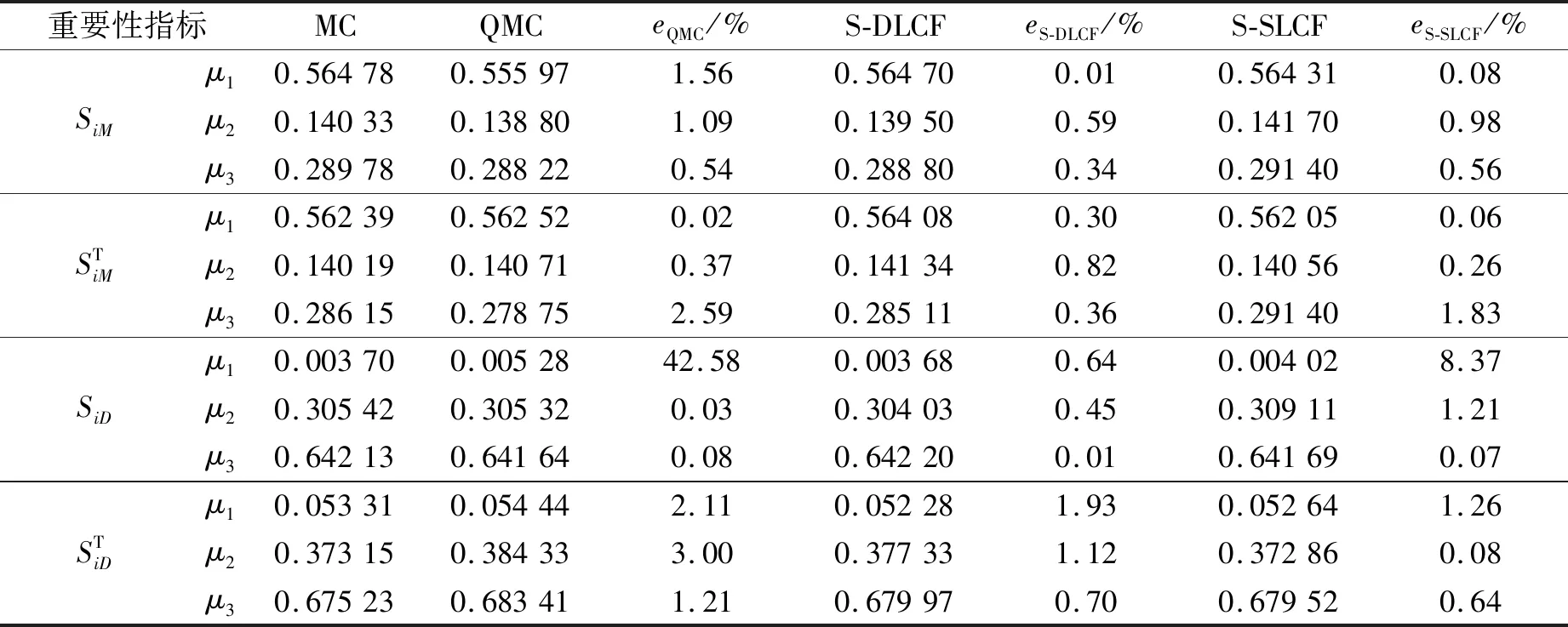
表3 算例3.1的重要性測度指標的計算結果

3.2 鉚接結構

在航空工業中,真實的鉚接過程非常復雜,本文以無頭鉚釘為例,將鉚接過程簡化為如圖1所示的2個階段。第Ⅰ階段中,鉚釘從狀態A(沖擊前的初始狀態,無變形)到狀態B(中間狀態,鉚釘和孔隙之間無縫隙)。第Ⅱ階段中,鉚釘從狀態B到狀態C(鉚釘受沖擊后的最終狀態,頭部被加工成型)。

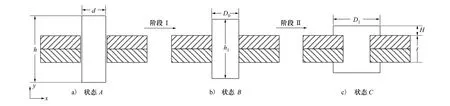
圖1 簡化的無頭鉚釘鉚接過程

為了建立鉚接過程中的鉚釘擠壓應力與幾何尺寸之間的數學關系,可以假設以下幾個理想條件:

1) 鉚接過程中鉚釘孔直徑不變

2) 鉚釘體積的改變忽略不計

3) 鉚接過程結束后,鉚釘的受力面為圓柱面

4) 鉚釘材料具有各向同性

鉚接前,圖1a)中的狀態A下鉚釘的初始體積V0可以由(18)式表示

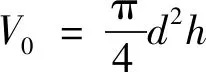
(18)

式中,d和h分別表示狀態A下鉚釘的直徑和長度。

第Ⅰ階段后,狀態B下鉚釘的體積可由(19)式表示為

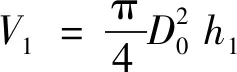
(19)

式中,D0和h1分別表示狀態B下鉚釘的直徑和長度。

第Ⅱ階段后,假設鉚釘在狀態C下的上下表面的尺寸相同,則狀態C下鉚釘的體積可由(20)式表示為

(20)

式中：t為薄壁件的整體厚度；D1和H分別表示狀態C下鉚釘頭的直徑和長度。

根據硬化強度理論,y方向上的最大擠壓應力σmax可以由(21)式表示為

σmax=K(εy)nSHE

(21)

式中：K為強度系數；nSHE為鉚釘材料的硬化因子；εy為鉚釘頭在鉚接過程中y方向上的真實應變。真實應變εy由第Ⅰ階段中產生的應變εy1和第Ⅱ階段中產生的應變εy2組成,因此,εy可由(22)式表示為

εy=εy1+εy2

(22)

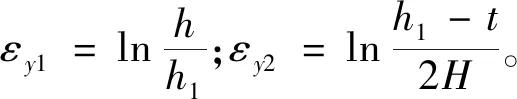
已經假設鉚釘在鉚接過程中體積不變,由(18)～(22)式可得鉚釘的最大擠壓應力可以由(23)式表示為

(23)

本文選取的鉚釘材料為2017-T4,其硬化指數nSHE=0.15。為保證鉚釘上下端有一定的余量,假設鉚釘頭高度H=2.2 mm。根據材料手冊,鉚釘的擠壓強度為σsq=565 MPa,如果最大擠壓應力大于擠壓強度,鉚釘就可能會失效,因此可以建立極限狀態方程如(24)式所示

g=σsq-σmax

(24)

在整個鉚接過程中,假設各隨機變量之間相互獨立且服從表4所示的正態分布,其均值存在主觀不確定性且服從表5所示的正態分布。

表4 無頭鉚釘的輸入變量的分布參數

表5 無頭鉚釘的輸入變量均值的分布參數

根據選取原則,該算例中輸入變量d,h,D0,t和K的SSPDF分別為N(5,0.62),N(20,2.52),N(5.1,0.1022),N(5,0.12)和N(547.2,16.4162)。

表6展示了4種方法得到的重要性測度指標以及每種方法所需調用功能函數的次數,從中可以得出,4種方法的計算量分別為5×(2 500)3,7×(30 000)2,181×10 000,18 000。從表中可以看出，相比于MC方法和QMC方法,S-DLCF方法和S-SLCF方法在滿足計算精度的前提下,2種新方法都能有效降低分布參數重要性分析過程中的計算量,并且S-SLCF方法比S-DLCF方法的計算量更少,表現了S-SLCF方法在重要性測度指標求解過程中更高的計算效率。

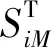
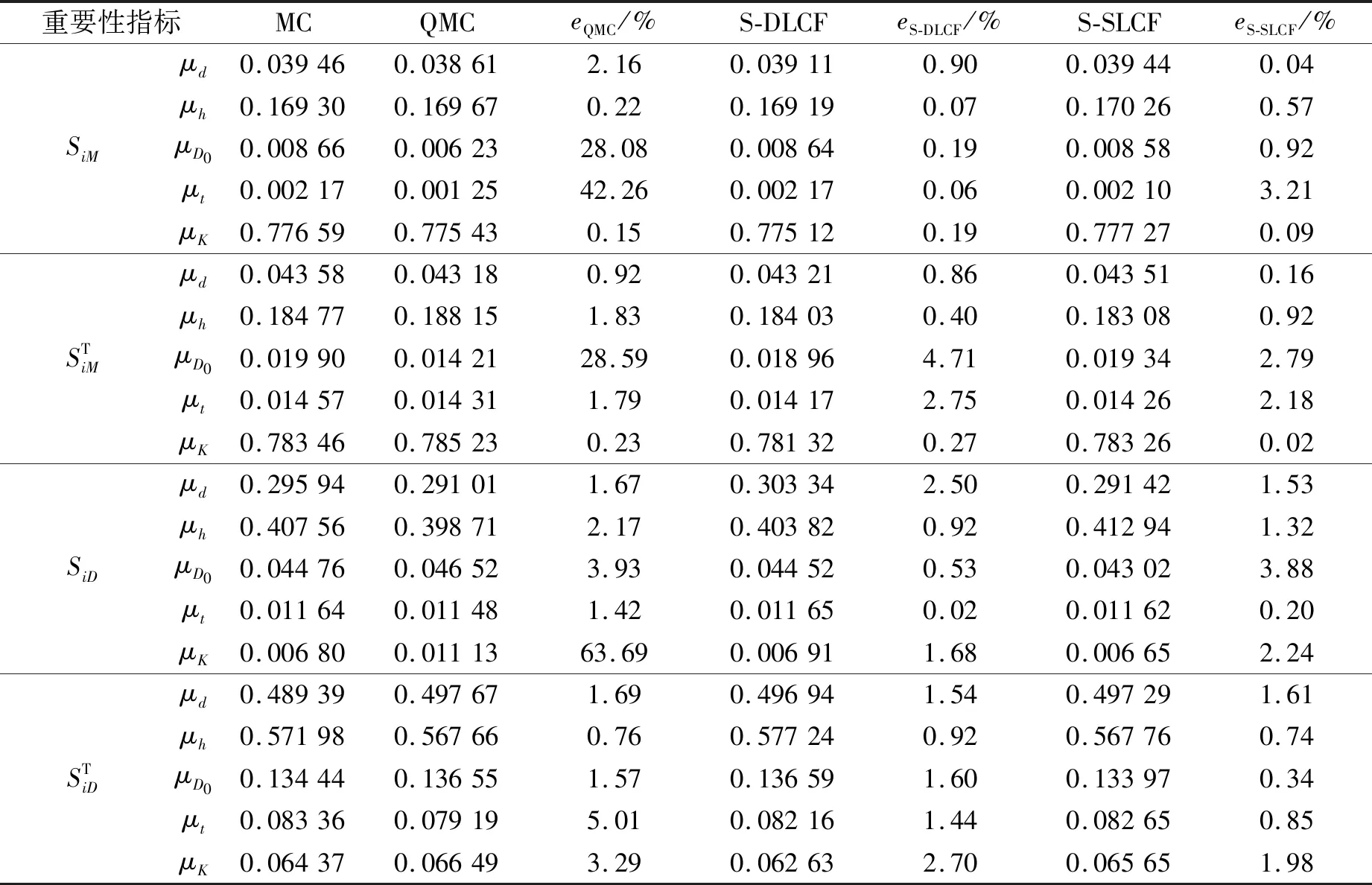
表6 算例3.2的重要性測度指標的計算結果

圖2 算例3.2在不同方法下計算得出的輸出均值重要性測度對比圖

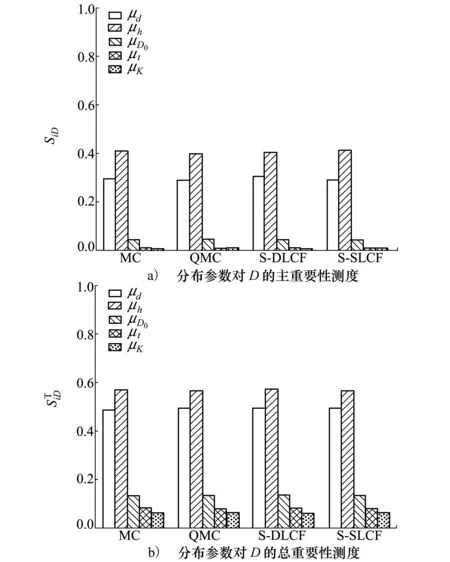
圖3 算例3.2在不同方法下計算得出的輸出方差重要性測度對比圖

4 結 論

本文研究了分布參數具有不確定性時的重要性分析問題,首先定義了衡量分布參數不確定性對輸出均值和方差影響的重要性測度指標。其次,針對傳統MC方法在進行參數重要性分析時計算量大、工程難以接受的缺點,以求積公式為基礎,結合SSPDF,提出了參數不確定性重要性測度求解的兩種新算法,大大降低了參數不確定性重要性分析的成本。

所提新算法的效率和精度取決于兩方面:一方面是CF的選擇,另一方面是SSPDF的選取。對于CF的選擇,依賴于問題的維數,本文選擇的是求積公式Ⅲ,該公式在求解低等到中等維度的問題時有較好的精度及效率;對于SSPDF的選取,一個合適的SSPDF應該覆蓋分布參數確定的輸入變量的整個變化范圍,本文采用了與原輸入變量具有相同分布的方法確定SSPDF。

通過數值算例和工程算例的分析結果可以得出,所提的新算法在求解主重要性測度和總重要性測度時都體現出了較高的精度,并能準確對分布參數的重要性進行排序。與QMC方法比較,2種新算法在大幅度減少計算量的同時表現出了更優的計算精度;而S-DLCF與S-SLCF相比,S-DLCF所得結果的相對誤差更小,計算結果更有效;而S-SLCF通過引入準蒙特卡洛法,真正意義上將求解分布參數不確定性下的重要性測度指標時的3層MC抽樣方法簡化為單層抽樣,計算過程更加簡潔。在工程實際中,可以根據具體的問題選擇不同的算法。