基于改進K-means算法和總時最短機制的無人機群多目標分配圍獵策略

胡濱,朱亞輝,杜致澤,趙子昕,周延年

(1.西北工業大學 自動化學院,陜西 西安,710072;2.陜西學前師范學院 數學與統計學院,陜西 西安 710061；3.西北工業大學 機電學院,陜西 西安,710072;4.交通運輸通信信息集團有限公司 衛星通信事業部,北京 100011;5.空軍工程大學 防空反導學院,陜西 西安 710043)

通過無人機之間的配合協作，無人機群能夠完成單體無人機難以應付的復雜問題[1]。空中目標圍獵是多無人機群的典型應用場景，它源于自然界中普遍存在的捕食狩獵行為，在多年的研究發展中對圍獵形式，圍獵目的進行了豐富的擴展[2-3]。其中多目標圍獵作為重要的戰術環節是目標圍獵的一個熱點問題，可以作為抓捕敵方重要人員或在對抗中壓制敵方重要目標的有力手段[4]。然而多目標圍獵任務涉及智能體較多，因此也更具有挑戰性。

多目標圍獵策略影響了任務整體實現的復雜度，合理的策略是實現成功圍獵的必要條件，因此對于無人機群多目標圍獵任務需要制定高效圍獵多個目標的策略。圍捕策略是一種特殊的編隊控制策略，根據不同目標數目，分為單目標圍獵和多目標圍獵。目前，協調多架無人機執行目標圍獵任務的研究方法主要有基于虛擬結構法、基于行為法、人工勢場法和圖論法。常見的單目標圍獵策略有受自然現象啟發的狼群捕獵模式。Muro等[5]參考狼群的狩獵過程，提出了一種多智能體協同圍獵模型。該模型對追捕者的溝通要求較低，同時不需要構建狼群中的等級制度來維持系統內秩序。Atamurat等[6]研究了在歐氏空間中所有個體速度相同情況下的單目標圍獵問題，對圍捕模型進行分析得出了圍獵成功的條件。Chen等[7]研究了高速逃逸目標的圍獵問題，給出了能夠成功圍獵的條件，包括所需執行者的最小數量、初始分布狀態以及圍捕策略。在多目標圍獵方面，Lopez等[8]對多智能體和多個動態目標的圍獵博弈進行研究，對所有博弈方設定最優策略，采用圖論方法為智能體分配控制策略，最后對有限時間內的圍獵效果做出分析。Amini等[9]提出了一種基于動態事件觸發機制的圍獵控制方法，利用分布式動態事件觸發結構，在降低通信量的同時實現非完整智能體系統的多目標圍獵任務。可以看出目前對于多目標圍獵的研究還不成熟，往往需要依賴復雜的計算和控制策略，而且許多研究是將多個目標考慮為一個整體進行分析，針對多個目標分別圍獵的研究較少。

處理復雜問題時，在全局中采用分布式、在局部采用集中式的方式在規模中等的任務分配中有較好的性能[10]。現階段對于單目標圍獵問題的研究比較成熟，且相對于多目標，單目標圍獵更容易實現。因此在無人機群圍獵多個獨立目標時，考慮將復雜的多目標圍獵問題通過聚類劃分轉換為多個簡單的單目標圍獵問題從而降低問題難度。常見的聚類算法有基于劃分的K-means[11]及Voronoi算法[12]、基于密度的DBSCAN[13]算法以及基于圖論的譜聚類算法[14]等。Elango等[15]利用K-means算法進行多機器人的任務分群從而最小化任務之間的距離。Bai等[16]分析了多種聚類算法，并提出將聚類策略與目標插入度量相結合的形式，保證了訪問所有目標位置的總旅行時間在一個合理的可計算上界內。選擇合適的算法有利于對多個目標進行快速劃分，K-means聚類算法應用廣泛，計算復雜度低，具有較好的收斂速度。因此本文使用K-means算法對多目標圍獵問題進行初步劃分。

圍獵的實現需要每個無人機個體執行明確的任務指令，即到達確定的位置。通過任務分配可以確定每個UAV需要執行的子任務。Wang等[17]研究了多智能體系統中協同控制的任務分配機制，指出通過協同分配協議可以在間歇通訊情況下得到較好的分配結果。Lee等[18]提出了一種面向資源的分散拍賣算法，該算法考慮了智能體的資源消耗問題以及有限通訊范圍問題。在分配任務時會出現沖突現象即同一個任務的最佳執行個體不唯一，此時就需要設計分配機制。設計準則可以是系統的資源消耗最少，任務完成的時間最短等。在實際情況中，防止目標在圍捕之前逃逸，將目標快速圍捕是最重要的。上述研究雖然可以實現最優解，但任務完成的總時間不一定最短。Bai等[19]研究了多個分散車輛訪問一組目標的動態任務分配問題，提出了基于事件觸發和時間觸發的2種動態任務分配算法。但該算法較為復雜。因此本文考慮無人機群中的個體在速度相同的情況下，以完成圍獵任務總時間最短為目標，設計任務分配算法并使該算法的計算量盡可能小。

本文主要研究適用于空中無人機群多目標圍獵任務分配策略的整體解決方案。為了得到更好的圍獵性能，采用混合式方法的思想，先利用分布式方法對系統進行分層處理，之后針對每個獨立的子系統利用局部的集中式方法完成圍捕任務的分配。通過對任務不斷細分，實現復雜任務的簡單化。

本文的創新點如下：

1) 改進了K-means法，通過該分布式算法可以將多目標圍獵問題分解為多個相互獨立的、能夠滿足圍獵條件的單目標圍獵系統。該算法計算量小、操作簡單，能夠處理大規模無人機群的任務分層。

2) 針對一個單目標圍獵子系統，通過任務分解使單體無人機只需完成簡單明確的子任務即可完成單目標的圍獵。考慮到實際圍獵情況，以完成圍獵任務的總耗時最少為決策條件，設計了一種任務分配策略，能夠以較少的計算量得到使任務完成時間最短的分配方案。

1 圍獵問題描述

首先給出單目標被成功圍獵的定義。當發現待圍獵目標時，目標周圍的n個UAV逐漸靠近,將目標限制在半徑為r的范圍內。根據圍獵的臨界條件[20],完成圍獵需要3個智能體分布在目標同一平面內,即為了確保目標被成功圍獵,須滿足n≥3。此時以待圍獵目標的位置pt為中心,在半徑r的圓上作內接n多邊形,當控制UAV占據多邊形的n個頂點形成圍獵陣型時可以認為圍獵成功。

考慮到實際情況,允許UAV的位置pu與多邊形頂點之間存在Δr的偏差。即

r-Δr≤‖pu-pt‖≤r+Δr

(1)

式中：pu為UAV的位置;pt為待圍獵目標位置。圍獵效果如圖1所示。

圖1 圍獵成功示意圖

2 任務分層與任務分配問題描述

通過任務分層可以將無人機群多目標圍獵問題分解成與待圍獵目標一一對應的多個單目標圍獵子系統。子系統結構更簡單且相互獨立,從而可以降低無人機群多目標圍獵系統的耦合性。子系統內部繼續對圍獵任務進行分解,將單目標圍獵任務分解成多個簡單的子任務并分配給具體的UAV個體。任務分層與任務分配問題如圖2所示。

圖2 任務分層與任務分配示意圖

考慮在無人機群多目標圍獵系統中有M個待圍獵目標,定義待圍獵目標個體的集合T為

T={ti|1≤i≤M}

(2)

同時空間中存在N個UAV,定義UAV個體的集合U為

U={uj|1≤j≤N}

(3)

為了保證所有的目標都能被成功圍獵,需要滿足N≥3M。

任務分層目標:分層結果需要保證每個待圍獵目標ti對應一個子系統Si,并且每個子系統中包含的UAV數量q需要滿足q≥3。子系統Si表示為

Si={uij|1≤i≤M,1≤j≤q}

(4)

子任務的集合表示為

S={Si|1≤i≤M}

(5)

任務分配是指:在圍獵子系統Si中,若存在q個UAV,則會對應q個子任務。子系統i中待分配的子任務tik的集合表示為

Ti={tik|1≤i≤M,1≤k≤q}

(6)

子系統i中的UAV個體uij可以對tik做出評價,評價的效用值用bijk表示。對于可以執行的任務bijk≥0,若不能執行tik,則bijk=0。把完成任務所需的時間作為評價指標時,uij完成tik的時間越短,則bijk的值越大。

任務分配問題可以描述為

(7)

且需滿足

(8)

通過(8)式可以保證子系統中的每個UAV都有需要待執行的子任務,同時每個待執行的子任務都必須由一個UAV去完成。

3 改進K-means算法的任務分層方法

傳統的K-means算法能夠對大量數據進行劃分,從而形成所需數目的數據簇,同一個簇中數據元素之間的相近度較高,經過該算法的劃分,每個數據只能隸屬于一個數據簇。該算法的劃分依據是最小誤差函數,該誤差函數可以描述各個數據與聚類中心的偏差情況。一般選用數據和中心的歐式距離作為誤差函數。

根據任務分層的要求,將K-means算進行改進。改進后的算法主要有以下特點:

1) 將N個待圍獵目標的坐標設置為聚類中心,并且該聚類中心不隨著算法的迭代而發生變化。

2) 劃分完成后分別判斷每個子系統內的UAV個數是否滿足要求,如果存在數量不滿足的子系統,則重新劃分。

改進的K-means算法步驟如下:

步驟1 設在空間R內存在由n個UAV組成的無人機群,以UAV位置坐標為元素的數據集記為p={p1,…,pn},同時存在m個待圍捕目標,將目標的位置坐標設置為初始的m個聚類中心,表示為pti,i∈{1,…,m}。用(9)式計算pj相對于pti的距離dij。

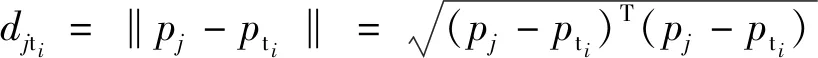
(9)

根據計算結果,pj會被規劃到距離最近的數據中心i所代表的數據簇Ci內。

Ci={pj|‖pj-pti‖≤‖pj-ptq‖,1≤q≤m}

(10)

步驟2 通過步驟1，初步形成m個子系統。之后判斷每個子系統內的UAV數量是否滿足要求。

步驟3 對于數量不滿足的子系統Se,計算不包含在子系統Se內的元素與屬于Se的聚類中心pte的距離,將距離該中心最近的元素劃分至Se。在調整子系統內元素數量時,可能出現子系統內的元素被抽離后,該子系統元素個數不滿足要求的情況,需要重新補充。為了防止同個元素被來回調動所造成的算法循環，需要限制被調動的元素不再考慮補充到原來的子系統中。

（19）分期出杳入宴，恍惚經緯萬方。（《太上說玄天大聖真武本傳神呪妙經註》卷二，《中華道藏》30/549）

步驟4 重復步驟2～3直至所有子系統內的元素滿足要求。

改進K-means算法的流程圖如圖3所示。

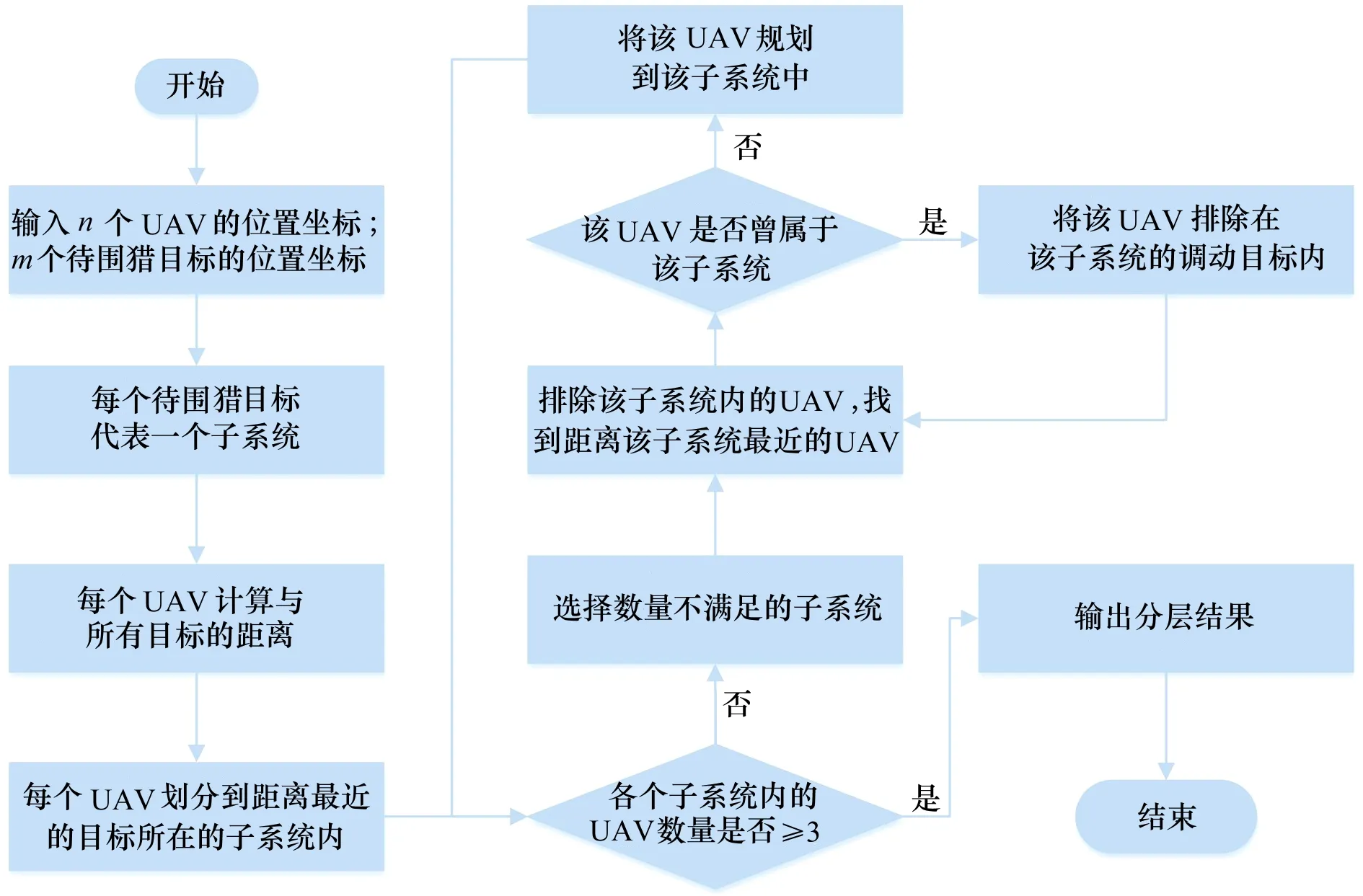
圖3 改進K-means算法流程圖

4 基于總時最短機制的任務分配策略

系統分層后,每個子系統需要根據UAV的數量規劃子任務并給出子任務的分配結果。通過設計任務分配機制,可以使整個系統得到能夠實現需要的較為優化的解。

本文的任務分配機制是優先考慮任務完成的總時間最短。子系統內UAV完成圍獵任務的總時間取決于完成子任務時間最長的UAV。假設同一子系統內的UAV同時執行任務且速度相同。這意味著UAV完成子任務需移動的距離d越短則完成子任務的用時t越少,即t∝d。基于上述設定,總時最短的分配機制可轉化為分配結果使UAV完成子任務移動的距離最大值是眾多分配方案中最小的。

對于一個包含q個UAV的子系統Si,任務分配算法步驟如下:

步驟1 選取距離待圍獵目標最近的UAV作為任務分配中心記為ui1,計算該UAV到半徑為r的圍獵圓上的最近點,并將該點設為圍獵圓的內接正q邊形的一個頂點z1。同時將該頂點位置作為子任務分配給ui1。

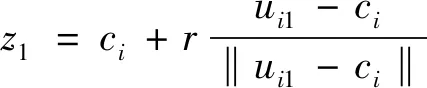
(11)

步驟2 任務分配中心計算得出其余q-1個頂點的位置。將q-1個頂點位置作為子任務集向其他UAV發布。UAV個體uij,j∈{2,…,q}到頂點zk,k∈{2,…,q}的距離記為dijk。每個UAV分別計算與q-1個頂點的距離,得到該UAV的距離數據集dij,任務分配中心對每個數據集進行匯總得到矩陣Ai,此時Ai∈R(q-1)×(q-1)。

(12)

步驟3 若uij執行子任務tik,則從矩陣Ai中刪除uij對應的列向量dij和子任務tik對應的行向量,此時Ai的階數減1。

步驟4 任務分配中心找到矩陣Ai中的最大值,該值對應的UAV完成子任務的時間最長。若最大值不唯一,則找出所有最大值對應的列向量中的最小值,最小值表示該值對應的UAV完成子任務用時最短。最小值對應的UAV和子任務相互匹配,同時進行一次步驟3。若最大值唯一,則找出最大值所在列向量中的最小值。若最小值不唯一,則先將該列向量排除,并重復步驟4,直到該列向量中的最小值唯一,最小值對應的UAV和子任務相匹配。

步驟5 循環步驟3～4,直到所有子任務分配完成。

任務分配的流程圖如圖4所示。

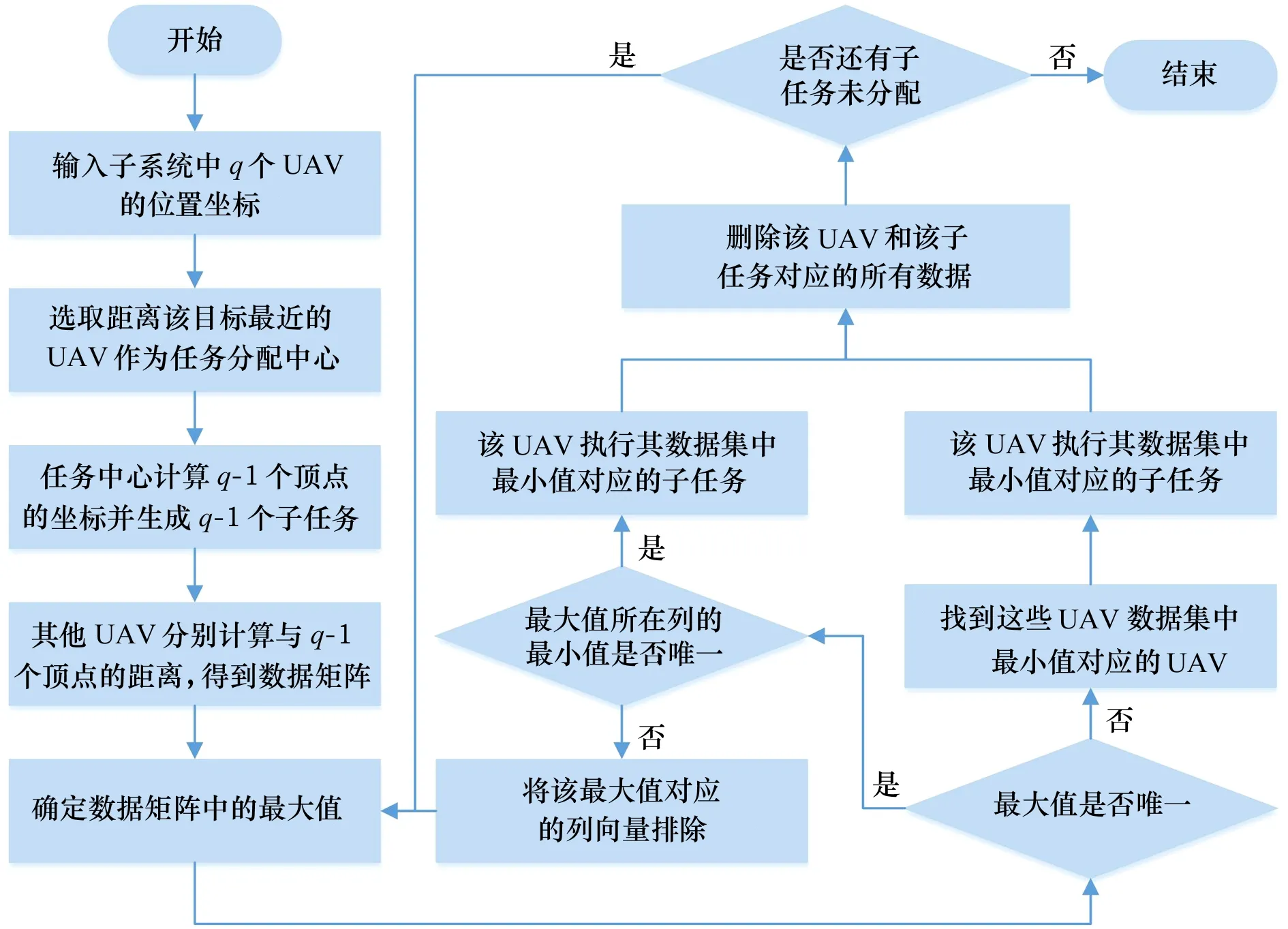
圖4 任務分配流程圖

5 實驗仿真

為了驗證本文提出的多目標圍獵策略的有效性,設計了一個仿真實驗，指派9個UAV分別圍獵3個目標。該系統的初始狀態如圖5所示。

圖5 多無人機圍獵系統初始狀態

UAV的位置是隨機確定的,表1～2給出了仿真中各UAV和待圍獵目標位置。

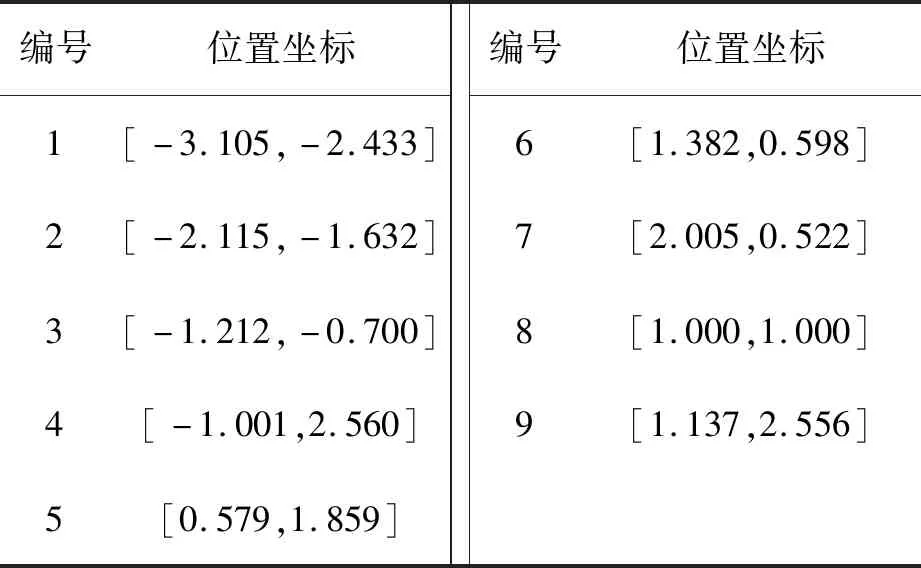
表1 仿真中各UAV位置

表2 仿真中待圍獵目標位置

根據第2節所述任務分層與任務分配策略,首先使用改進的K-means算法對系統進行分層,分層效果如圖6所示。可以看出,分層算法能夠生成與待圍獵目標數量相同的子系統,并且能夠對數目不滿足的子系統進行補全。由圖6b)～6c)可以看出,被調動過的UAV不會被重復調動,最終使得每個子系統都滿足成功圍獵的要求。

系統分層后每個子系統進行子任務的生成與分配,為了比較本文提出總時分配機制的性能,同時使用匈牙利算法對子任務進行分配。基于總時最短機制的分配結果如圖7所示。基于匈牙利算法的分配結果如圖8所示。

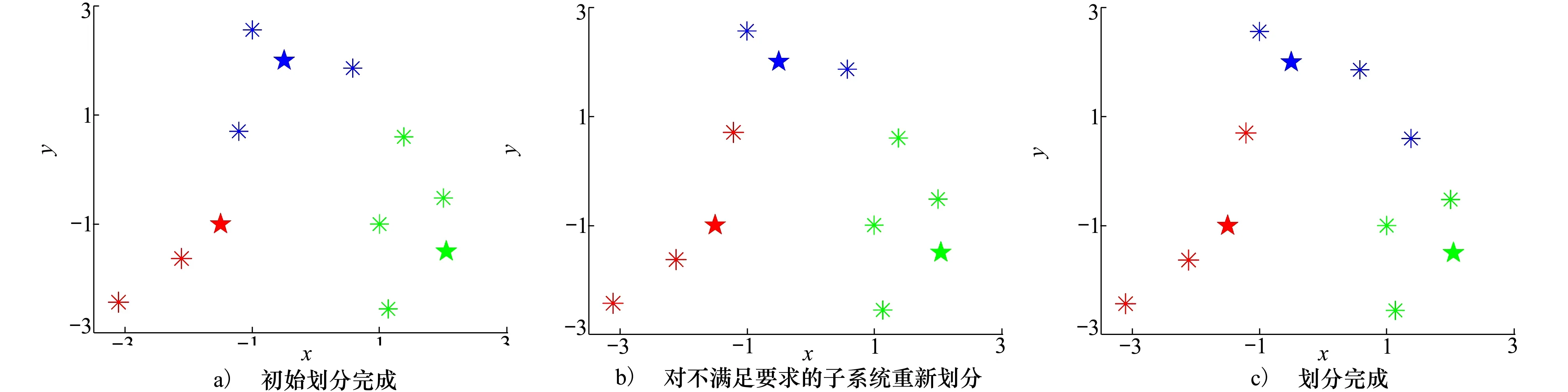
圖6 任務分層效果

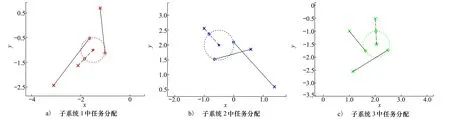
圖7 各子系統基于總時最短機制的任務分解結果

圖8 各子系統基于匈牙利算法的任務分解結果

各子系統內子任務對應的坐標如表3所示,任務分配中心對應子任務為1號子任務,其他子任務按照順時針進行編號。

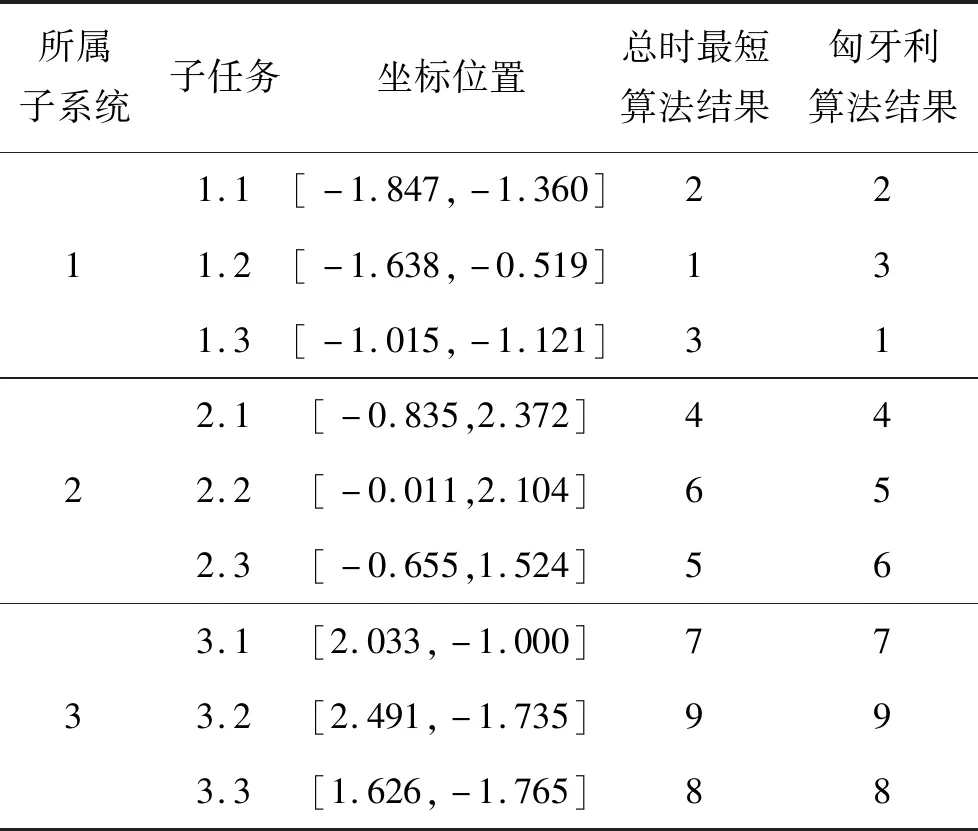
表3 各子系統中各子任務位置及對應關系

為了分析2種算法的效果,比較了2種分配結果對應的完成圍獵任務的總時間,為了方便計算,設智能體的速度都為1,結果保留2位小數,如表4所示。結果表明本文提出的分配算法能夠滿足總時最短的要求。

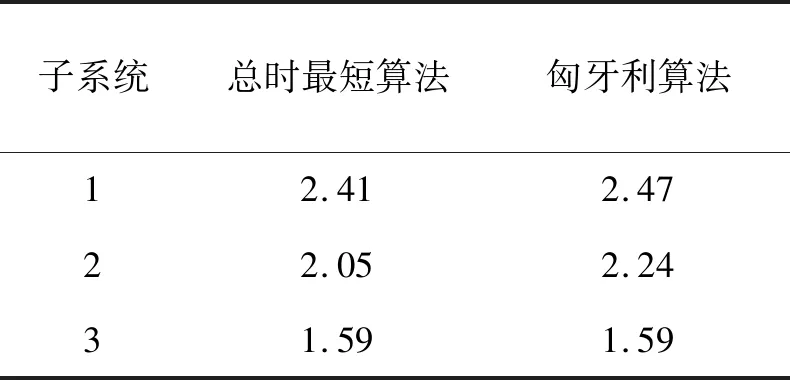
表4 2種算法的完成任務用時對比

根據仿真結果可以看出本文提出的任務分配策略會選擇總時最短的分配方案,例如圖7b)所示子系統2的分配情況,子任務2.2對于5號UAV和6號UAV都是距離最近的子任務。因此會出現分配沖突,此時通過計算,6號UAV完成子任務2.3的時間比5號UAV完成子任務2.3的時間更長,因此為了使完成任務的時間最短,將子任務2.2分配給6號UAV。

6 結 論

本文提出的多目標任務分配策略將復雜的系統逐步分解為多個簡單子任務,將計算任務分散在單體UAV上,提高了系統的靈活性。該策略首先通過改進K-means算法使系統分層形成多個子系統,實現系統的解耦。之后每個子系統作為單獨的任務單元將任務細分并以完成任務的總時間為主要考慮因素對子任務進行分配,使UAV在最短時間內完成目標的圍獵任務。通過仿真實驗可以證明該策略易行且有效。