可調數目吸引子共存的混沌系統及同步控制

顏閩秀，謝俊紅

(沈陽化工大學 a.信息工程學院； b. 工業環境-資源協同控制與優化技術遼寧省高校重點實驗室，沈陽 110142)

0 引言

混沌系統是隨時間不可預測的系統，對初始條件和參數的變化具有極端的敏感性。混沌用于許多非線性科學領域，如信息處理、安全通信等[1-2]。最近幾年，一些非線性混沌動力系統的研究成為熱點。如Hyperjerk系統、多穩態、共存吸引子混沌系統等[3-5]。這些混沌系統可以分為兩個主要類別：一是具有自我激發吸引子的系統類別；二是具有隱藏吸引子的系統類別。值得注意的是，有自我激發吸引子和隱藏吸引子兩者都存在的系統。如何生成混沌系統是個有趣的方向。

一種是在簡單的數學模型中發現非線性系統中的混沌，最具有代表性的是SprootB構造了含有五項式和兩個非線性項以及六項式和一個非線性項的混沌系統[6]。另一種方法構造具有特殊奇異吸引子的混沌系統，如多渦卷吸引子、多翼吸引子等[7-8]。平衡點的個數在一定程度上決定了動力學性質。一般認為，沒有平衡點的混沌系統能夠產生隱藏吸引子。大量的研究表明，具有多個不穩定平衡點的混沌系統往往具有更豐富的動力學行為且更容易產生吸引子的共存。因此許多學者傾向于構造混沌系統，并通過平衡點的類型來區分動力學特性，如鞍點、不穩定焦點和其他類型平衡點的混沌系統[9-11]。

近期，混沌系統中吸引子的共存引起了學者們的廣泛關注。Li等[12-13]通過數值實驗研究了Lorenz混沌系統中的吸引子的共存，并提出了產生共存吸引的方法。Kengne等[14]提出了Jerk系統中吸引子的共存。Bao等[15-16]發現，基于憶阻器的混沌系統可以產生不同類型的共存吸引子。Li等[17-18]深入研究了基于憶阻器的混沌系統中的共存吸引子，并考慮將其應用在圖像加密中。基于以上研究，不難發現，較傳統的混沌系統，具有吸引子共存的混沌系統動態行為更加復雜，應用在同步通信中具有較好的潛力。因此，提出具有吸引子共存的混沌系統是有意義的。從建立具有簡單系統和復雜行為的角度出發，提出了一個具有無限多吸引子共存的混沌系統，且將雙曲正切函數加入該系統，并對該系統的動態特性進行了必要的理論和實驗研究。研究表明該系統所產生的吸引子共存具有可調性，理論研究上能夠產生無限多的吸引子共存。此外，將主動反推全局同步控制的方法應用在該系統中。該主動控制方法是以嚴格反饋設計的形式實現控制系統平衡點鎮定的遞推過程，反推同步控制方法廣泛應用于非線性系統的控制中[19-20]。進一步，設計了反饋控制律，然后對反饋控制律進行修正，進而設計出真正的控制器，實現了系統的全局同步控制。

1 系統模型

建立系統模型為

(1)

其中，x1,x2,x3為狀態變量，a,b為系統常數，當a=-1.5,b=15,c=2,d=0.5時，系統(1)為混沌系統。在仿真中，將初值取為(0.1，0.1，0.1)，圖1展現了系統(1)的吸引子。

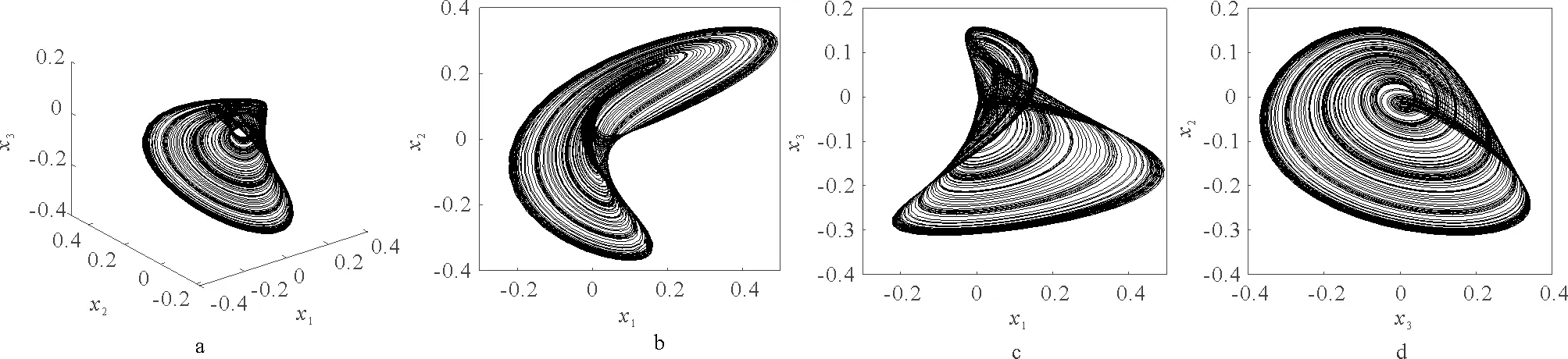
圖1 系統(1)的相圖Fig.1 Phase diagram of system (1)

當參數a=-1.5,b=15,c=2,d=0.5時，計算出系統(1)的李雅普諾夫指數為

L1=0.15,L2=0,L3=-1.17

(2)

通過式(2)可看出，最大李雅普諾夫指數為L1=0.15且指數之和總是為負數。

計算李雅普諾夫維數得到

(3)

其中,j滿足最大整數為

(4)

根據式(2)和式(3)看出，李雅普諾夫指數為(+,0,-)且維數為分數維，符合混沌系統的基本性質。

為了再次驗證系統(1)為混沌系統，選取a作為控制參數，通過MATLAB繪制其分岔圖和李雅普諾夫指數圖，如圖2所示。

圖2展現了系統(1)在a∈[-3,-1]區間的分岔圖及李雅普諾夫指數譜。圖2a分岔圖表明系統(1)在a∈[-3,-1]區間內系統由周期運動進入混沌運動。當a=-1.5時，圖2a的分岔圖中有成片的密集點且相對應的圖2b的李雅普諾夫指數為(+,0,-)，再次說明了系統(1)是混沌的。

系統復雜度的特性是應用在通信領域中的重要理論基礎，為了驗證該混沌系統的復雜行為，以譜熵(SE)為例，SE采用傅式變換并與Shannon熵進行結合得到SE的值，具體算法如下所示。

步驟1去直流。偽隨機序列的長度為N，利用式(5)除掉其中直流部分，能量的信號能夠被頻譜更加精確地表現。

(5)

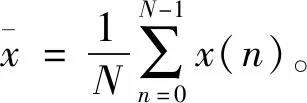
步驟2對x(n)進行離散傅式轉換。

(6)

其中，k=0,1,2,…,N-1。

步驟3計算相對功率譜，依據式(6)中的X(k)序列前半部分，根據Paserval定理，計算某個特定的頻率點功率譜。

(7)

其中，k=0,1,2,…,N/2-1

序列的總功率

(8)

那么，相對功率譜概率

(9)

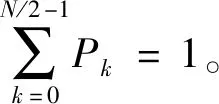
步驟4根據式(7)、(8)和(9)，并與Shannon熵進行結合，計算信號的譜熵

(10)

若PK=0，則PKlnPK=0，se的大小將在ln(N/2)處收斂，為了便于分析se，將其進行歸一化處理

(11)

可見，若序列的振幅不明顯，則說明結構簡單，那么，所得到的譜熵值也就越小，相應地，復雜度也就越小，否則，復雜度就越大。

根據上述SE算法，對系統(1)進行了計算，并于圖3展示了SE的計算結果。

圖3展示了系統(1)在a∈[-3,-1]區間譜熵的復雜度，譜熵的最大測量值接近于0.7且振幅較為明顯，因此，復雜度相對較高。一般地，譜熵的復雜度有明顯下降時，系統為周期態，反之，系統為混沌態，該仿真實驗結果與圖2基本一致。

圖2 系統的動態特性Fig.2 Dynamic characteristics of the system

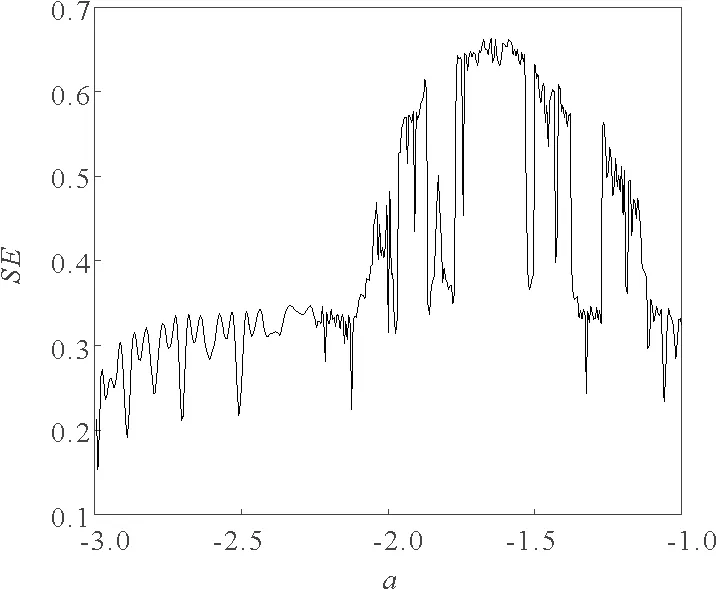
圖3 SE復雜度Fig.3 SE complexity

2 可調數目的吸引子共存

基于系統(1)，為了使具有可調數目的吸引子共存，考慮建立雙曲正切函數的序列用于生成具有無限吸引子共存的混沌系統，建立函數

(12)

其中，n為非負整數，參數λ可調節，此時取λ=100。可看出，隨著n增大，函數θi(xi)的零點得到擴展。利用θ1(x1)取代系統(1)中等式右邊的x1，那么在特定參數下，得到的新系統將會沿x1的方向產生共存吸引子。

首先，考慮沿x1軸的方向產生共存的吸引子，利用θ1(x1)取代系統(1)中等式右邊的x1，得到系統

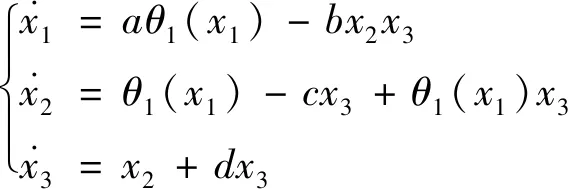
(13)

系統(1)將會沿x1的方向產生混沌吸引子的共存，如圖4所示，分別給出了n=0,1時的系統(1)的吸引子共存。

圖4a和b分別展示了n=0和n=1時的混沌共存吸引子，其中，圖4a中的混沌共存吸引子對應的初值為(2i-3,0.1,-0.1)，其中i=1,2，圖4b中的混沌共存吸引子對應的初值為(2i-5,0.1,-0.1)，其中i=1,2,3,4。這些混沌吸引子的共存形狀相似，但是軌跡并不相同。若繼續增大n，系統將會沿x1軸方向產生更多的混沌吸引子共存。

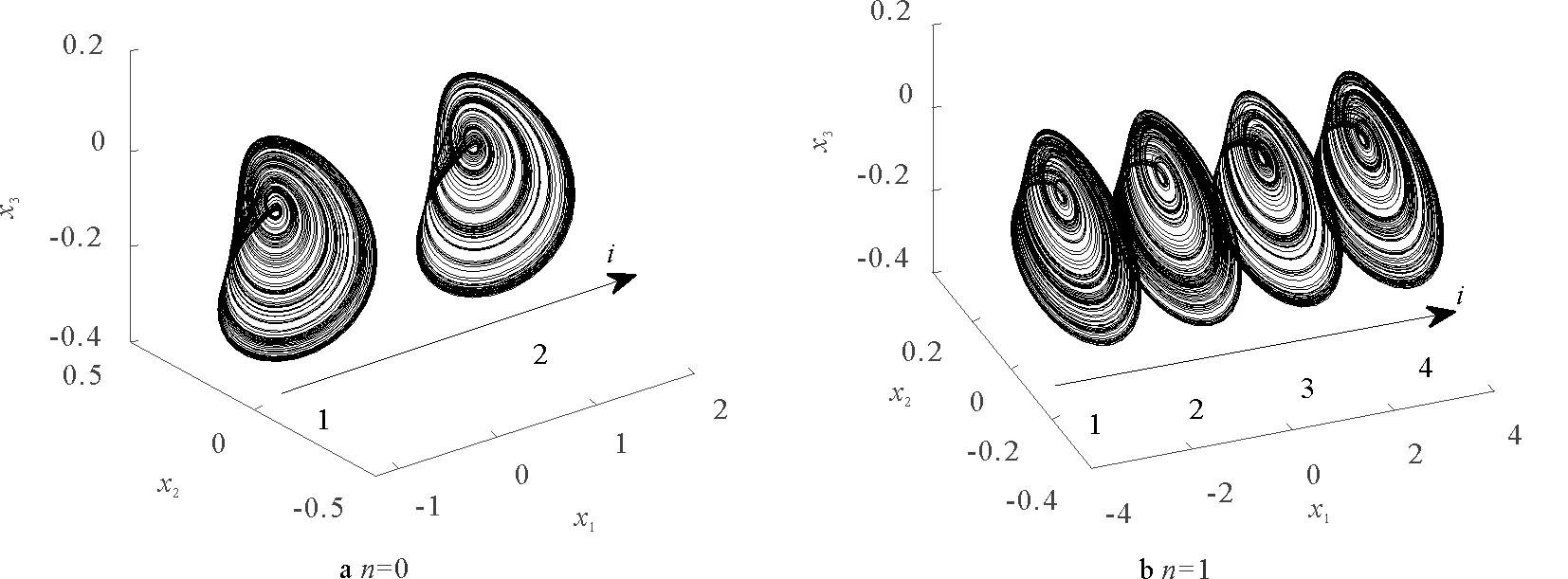
圖4 混沌吸引子共存 Fig.4 Coexistence of chaotic attractors

其次，考慮用H2(x2)取代系統(13)中等式右邊的x2，得到系統(14)

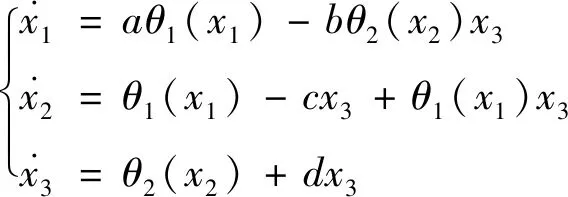
(14)

系統(14)將會沿x1和x2軸方向產生共存的混沌吸引子，圖5分別給出了參數n=0,1時的吸引子。

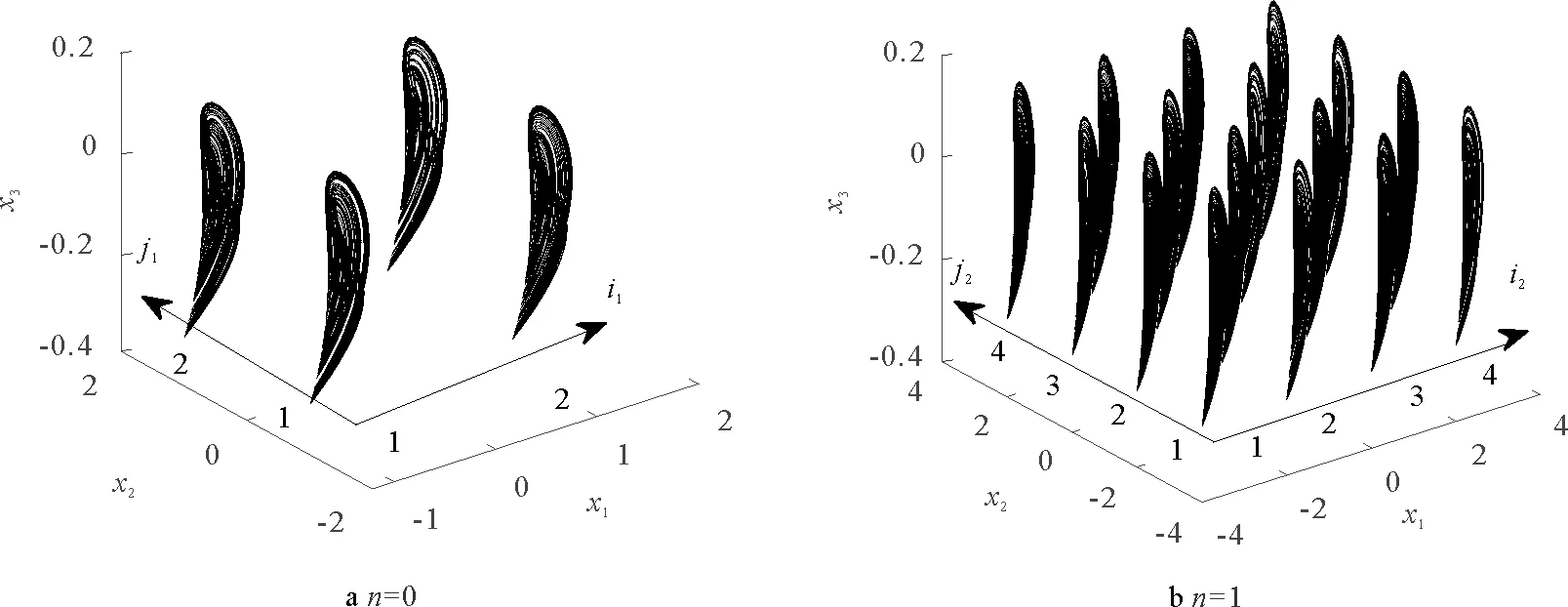
圖5 x1和x2軸上的吸引子共存 Fig.5 Coexistence of attractors on x1 and x2 axes

圖5a和b分別展示了2×2,4×4的吸引子，這些吸引子對應的初始條件分別為(2i1-3,2j1-3,-0.1),(2i2-5,2j2-5,-0.1)，其中，i1,j1=1,2，i2,j2=1,2,3,4。

最后，考慮用H3(x3)取代系統(14)中等式右邊的x3，得到系統(15)：

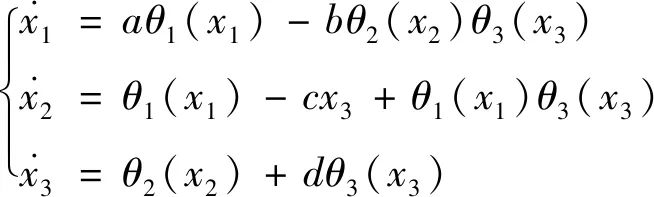
(15)

系統(15)將會沿x1、x2和x3軸方向產生共存的混沌吸引子，圖6分別給出了當n=0,1時的系統(15)的吸引子。

圖6a和b分別展示了2×2×2,4×4×4的吸引子，它們所對應的初始值分別為(2i1-3,2j1-3,2k1-2.8),(2i2-5,2j2-5,2k2-4.8)，其中，i1,j1,k1=1,2，i2,j2,k2=1,2,3,4。

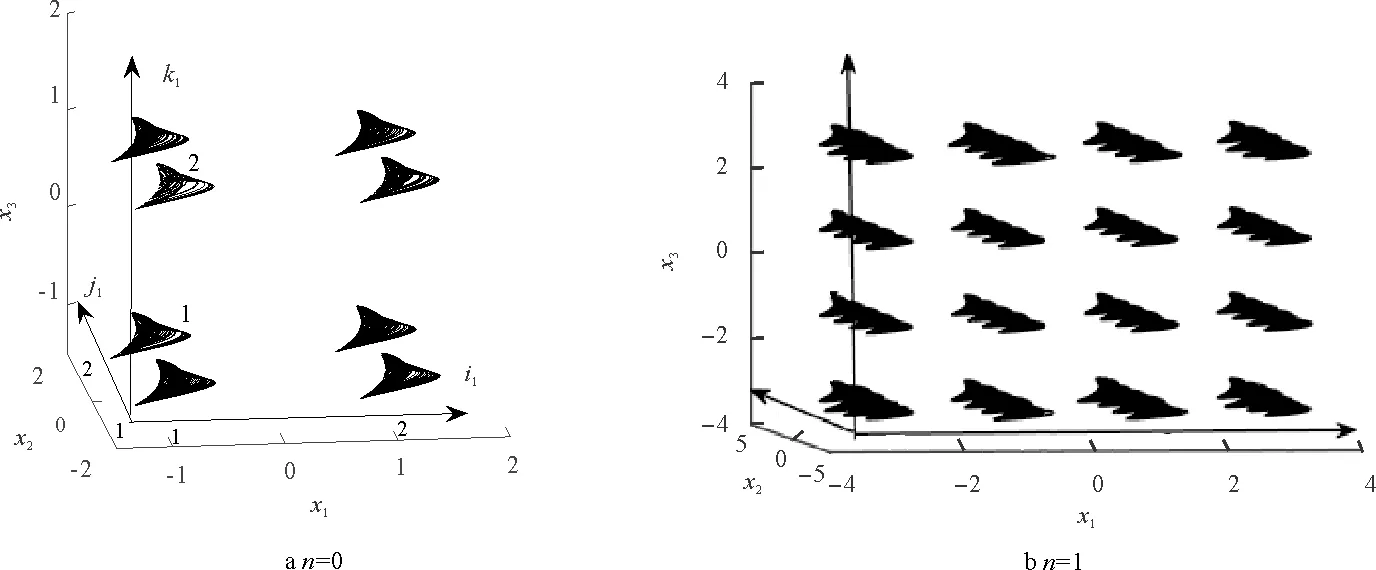
圖6 x1、x2和x3軸方向上的吸引子共存Fig.6 Coexistence of attractors on x1,x2 and x3axes

通過上述研究表明，系統(1)在函數(12)的作用下，通過調整n可以改變吸引子共存的生成個數。通常，若沿r個方向來產生吸引子的共存，系統(13)(14)(15)生成的吸引子共存個數至少為Nr=(2n+2)r,r=1,2,3。當n→∞,Nr→∞時，即吸引子共存個數趨近于無限多個。

3 混沌系統的主動反推全局同步控制

反推控制的設計方法是針對不確定系統的一種系統化的控制器綜合方法，它能夠應用在線性系統與非線性系統中。特別地，應用在非線性復雜系統中時，它能使在線計算時間的目的減少，同時，通過設計反推使得V函數和控制器的設計過程系統化及結構化。

這里，基于含有雙曲正切函數的系統(14)，采用主動反推同步控制的方法用于實現非線性復雜系統的同步控制。

選取系統(14)為驅動系統，如式(16)：

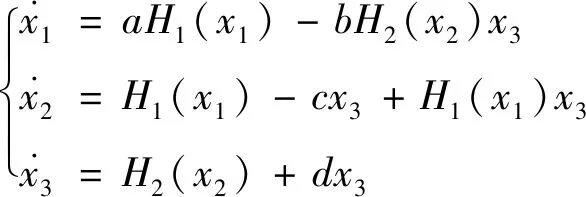
(16)

其中，x1,x2,x3為狀態變量，a,b,c,d為系統的參數。

相應的響應系統如式(17)：

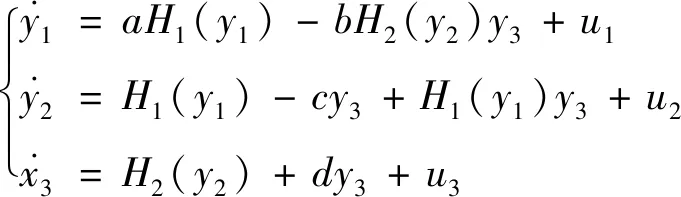
(17)

其中，yi為狀態變量，ui是反饋控制律，i=1,2,3。

系統(16)和系統(17)之間的同步誤差定義為

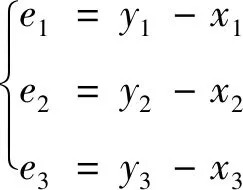
(18)

同步誤差系統為

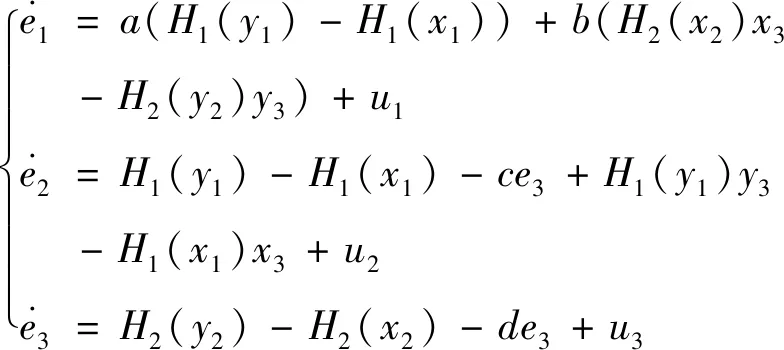
(19)

考慮設計反饋制律為

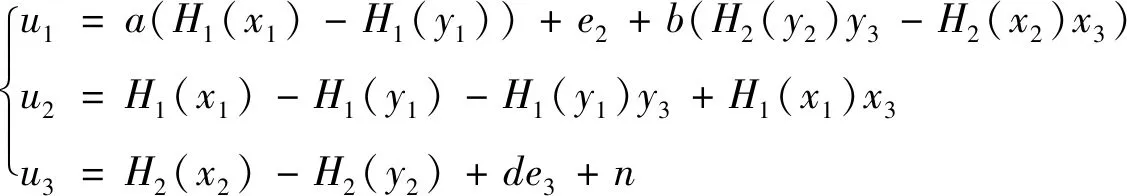
(20)

將式(20)代入式(19)，誤差系統簡化為

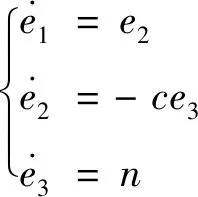
(21)

選取李雅普諾夫函數為

(22)

其中，

θ1=e1

(23)

對式(22)進行求導得到

(24)

其中，令：

θ2=e1+e2

(25)

簡化式(24)為

(26)

接下來，選取李雅普諾夫函數為

(27)

進行求導得到

(28)

同理，

(29)

經過反推得到

(30)

令n=-3e1-5e2-3e3-kθ3，得到

N=-kθ3

(31)

將式(30)代入式(29)得到

(32)

其中，它在R6上是半正定和二次的函數。

根據李雅普諾夫穩定性理論可知， 當t→∞時，全部的ei(0)∈R,(i=1,2,3),誤差系統ei(t)→0,(i=1,2,3)。誤差系統全局漸近穩定，驅動與響應系統實現全局同步。

最后，將反饋控制律更新為

(33)

圖7 系統(16)和(17)誤差同步Fig.7 Error synchronization of system (16) and (17)

其中，k為控制增益，k>0，控制增益k取值越大，同步誤差收斂于零的速度越快，所需要的時間就越短。如圖7所示，系統(16)和(17)實現誤差同步。

數值仿真實驗時，選擇參數(a,b,c,d)=(1.5,15,2,0.5)，控制增益k=20，初值驅動系統X(0)=(0.1,0.1,0.1)和響應初值Y(0)=(5.8,-4.9,-1)。

圖7表明誤差同步在較短的時間內收斂于零。數值分析和實驗結果一致。驗證了該方法的有效性。

4 結論和展望

本文提出了一種模型較為簡單的混沌系統。描述了該系統的基本特性，為能夠生成混沌吸引子提供了基礎。進一步地，將雙曲正切函數加入該系統，使得該系統能夠產生無限多吸引子共存且吸引子的個數具有可調性。理論研究表明該系統能夠生成無限多個吸引子的共存，為生成無限多吸引子共存的混沌系統提供了理論依據。此外，在含有雙曲正切函數系統的基礎上設計了反饋控制律及系統的控制器，實現了系統的全局同步控制。理論研究和數值模擬仿真驗證了主要研究結果。該系統具有無限多個可調數目的吸引子共存，與傳統混沌系統相比其動力學行為更復雜。下一步計劃將其應用在安全通信中。