變體制導炮彈氣動特性分析及彈道仿真

賈 昂,王旭剛,李廣才

(1.南京理工大學 能源與動力工程學院,江蘇 南京 210094;2.淮海工業集團有限公司,山西 長治 046000)

變體飛行器在飛行過程中能夠改變局部或整體外形,實時適應多種任務需求,在多種飛行環境下保持最優的飛行效率和氣動性能[1]。

將變體技術應用于飛機或無人機設計中,國內外已經開展了很多的研究[2-6]。對于巡航導彈,目前已經對變后(前)掠巡航導彈、變展長巡航導彈、組合變形翼巡航導彈、傾斜翼巡航導彈等開展了研究[7-13]。文獻[14]對變體技術在助推-滑翔飛行器(高超聲速飛行器的典型代表)上的應用前景進行分析。

大口徑制導炮彈具有威力大、打擊精度高、性價比高等優勢,通過引入變體飛行技術可大幅度提高其射程,進而提升大口徑火炮在未來戰爭中的遠程精確打擊和超遠程火力壓制的能力,具有重要的研究意義。

文獻[15,16]分別針對亞音速條件和超音速條件設計了變后掠翼導彈氣動外形,總結了彈翼后掠角變化與氣動參數之間的關系。王旭剛等[17]為不同飛行階段的變后掠翼巡航導彈設計了彈道和控制指令,仿真結果表明所設計的彈道及指令合理,并且制導精度高。針對變后掠翼航彈的彈道優化問題,趙日等[18]采用粒子群算法對不同投放條件下的滑翔彈道進行優化設計,結果表明超音速投放相比亞音速投放增程效果明顯。為提高變后掠翼導彈的末速,文獻[19]基于hp-自適應偽譜法對其末端彈道進行優化,采用后掠角和攻角雙變量控制方案,建立多約束條件下的彈道優化模型,提出求解策略,結果表明導彈能夠在保證命中精度的同時落速更大,落角更佳。

本文為增加制導炮彈的射程,將變體飛行技術應用于滑翔增程制導炮彈的設計中,結合可變形彈翼,設計了一種變體制導炮彈。首先經過迭代優化設計變體制導炮彈的氣動外形,描述變體制導炮彈的控制方式和彈道特點;隨后利用工程化算法計算炮彈在不同彈翼外形時的氣動參數,同時對氣動特性及操縱特性隨后掠角的變化規律進行分析;最后為充分發揮變體制導炮彈的性能,基于氣動特性分析的結果制定炮彈飛行過程中的變體策略,并采用hp-自適應偽譜法對變體制導炮彈和固定外形制導炮彈的滑翔段彈道以射程最遠為目標進行優化和對比。

1 變體制導炮彈設計

1.1 變體制導炮彈氣動外形設計

為提高控制效率,減小舵面鉸鏈力矩,限制制導炮彈跨聲速飛行時的靜穩定性,本文設計的變體制導炮彈采用鴨式布局。變體制導炮彈的主要目標是為了增大射程,因此滿足穩定性和操縱性要求的前提下,以射程為目標迭代優化設計變體制導炮彈的氣動外形,設計流程圖如下。

變體制導炮彈長度為2 m。為使炮彈頭部器件布置合理并減小波阻,頭部采用卡門形母線,長徑比為2.6;為減小彈身中段空氣阻力,同時保證足夠的空間來容納各種彈載設備以及變形機構、火箭助推發動機等,彈身中段選擇常規的圓柱形,長徑比達到10.3。對于帶有火箭發動機的增程炮彈,一般采用較小船尾角船尾或者無船尾的尾部設計,故尾部采用圓柱式無船尾角的設計。

為了保證氣動特性、操控性和結構強度,變體制導炮彈選用根梢比大的梯形舵面;為了滿足變體制導炮彈在升弧段増加彈丸的穩定性同時對彈丸進行減旋的需要,尾翼翼展應盡量小。

彈體中部有“一”字型排列的可變形彈翼,與常規固定外形彈翼不同,變形彈翼采用機械結構搭配柔性蒙皮,彈翼形狀隨飛行環境和飛行任務改變(彈翼后掠角改變的同時會改變翼展和翼面積)進而獲得最優的飛行性能。

在其他幾何參數固定時,彈翼根梢比對空氣動力特性影響較小,三角翼(根梢比無窮大)的升阻比比梯形翼大,故采用三角形彈翼。三角形彈翼過小的后掠角對應大的翼展,提供較大的升阻比,但同時導致制導炮彈的操縱性較差。而過大的后掠角對提高升力效果不明顯,經過迭代優化設計,彈翼后掠角變化范圍在30～60°,最終確定的變體制導炮彈外形如圖2所示。

圖1 變體制導炮彈氣動外形設計流程圖Fig.1 Flow chart of aerodynamic shape design of morphing guided projectile

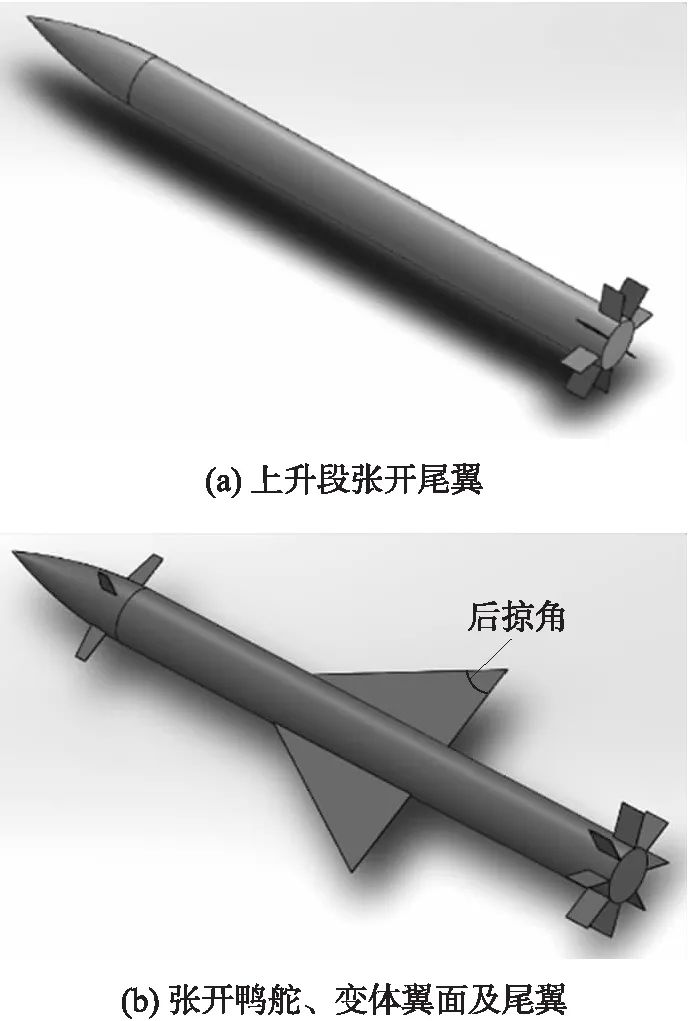
圖2 變體制導炮彈外形圖Fig.2 Shape diagram of morphing guided projectile

1.2 變體制導炮彈控制方式

變體制導炮彈采用鴨式布局,頭部兩對“十”字形布置的鴨舵分別對俯仰和偏航方向進行控制。由于鴨舵會對彈翼和尾翼產生下洗影響,因此結合鴨舵控制滾轉效率不高和變體制導炮彈彈翼外形可變的特點,提出一種通過彈翼的非對稱變形來提供滾轉控制力矩的方法:當一側彈翼后掠角增大導致彈翼面積減小時,該彈翼受到的升力減小,另一側彈翼外形保持不變則其受到的升力基本不變,兩側彈翼上的升力差將產生滾轉力矩,控制炮彈滾轉方向穩定。

1.3 變體制導炮彈彈道特點

變體制導炮彈采用火箭助推與滑翔增程相結合的復合增程方式。炮彈發射出炮口后折疊尾翼張開(如圖2(a)所示)保持穩定飛行,隨后火箭發動機點火,推動彈丸(爬高)增程。火箭發動機工作結束后炮彈繼續爬升飛行,期間彈道參數探測系統開始工作,到彈道頂點前后彈上鴨舵及變形翼面打開(如圖2(b)所示)。隨后變體制導炮彈根據操控指令控制舵面偏轉和彈翼變形,操縱彈體姿態使其滑翔至彈道終點。

與常規的制導炮彈不同,由于可變形彈翼大幅提高了炮彈的升阻比,并且在滑翔階段采用了變體飛行技術保持氣動特性較優,使得變體制導炮彈的射程得到顯著提升。

2 變體制導炮彈氣動特性分析

本文利用現有的工程化算法,基于模塊化思想,以大量實際試驗數據為基礎,結合部件組合法對炮彈氣動力進行快速估算,與一般工程估算方法和經驗公式的計算結果相比,具有適應性強和精度高的優點。

假設任一瞬時彈翼受力僅與飛行姿態及外形有關,與氣動力變化過程無關,對其氣動特性進行分析。

2.1 升阻特性分析

分別計算炮彈彈翼后掠角在30°、40°、50°、60°時不同馬赫數及攻角對應的升力系數和阻力系數。

變體制導炮彈升力系數隨馬赫數和攻角變化如圖3所示。分析可知,變體制導炮彈的升力系數與攻角呈線性關系,隨攻角增大而增大;不同后掠角外形升力系數隨馬赫數變化的趨勢一致,隨馬赫數增大先增大后減小。以60°后掠角外形、6°攻角為例,馬赫數由0.5增大到0.8時,升力系數由3.68增大到4.22,馬赫數達到1.2時升力系數為4.31,馬赫數達到1.5時升力系數又減小為3.59。

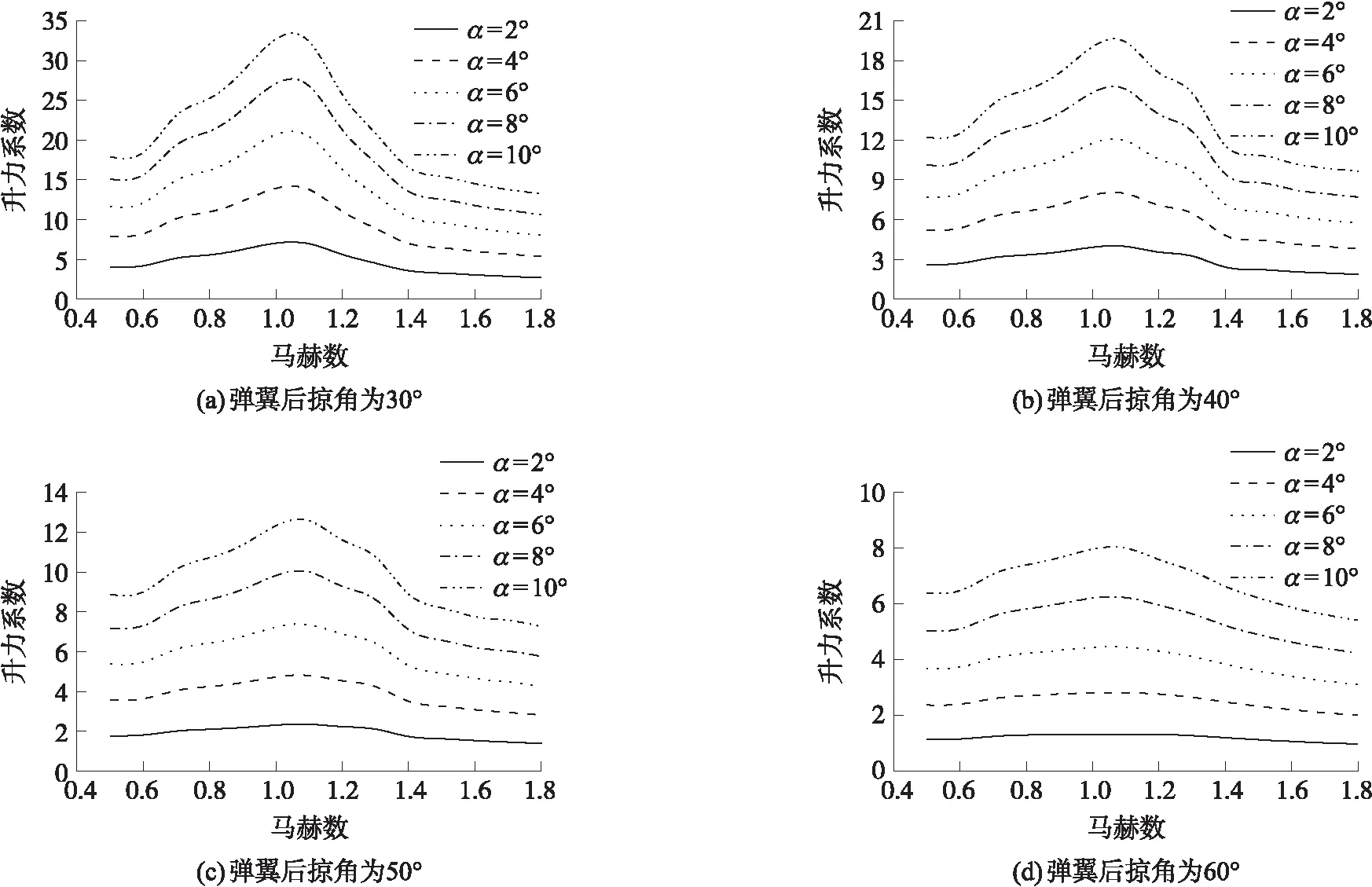
圖3 不同彈翼后掠角時炮彈升力系數變化Fig.3 Variation of lift coefficient with different sweep angles

變體制導炮彈的阻力系數隨馬赫數和攻角變化如圖4所示。分析可知,不同后掠角外形阻力系數的變化規律同升力系數相似,隨攻角增大而增大,隨馬赫數先增大后減小。以60°后掠角外形、6°攻角為例,馬赫數由0.5增大到0.8時,阻力系數由0.69增大到0.84,馬赫數達到1.2時阻力系數增大到3.48,馬赫數到1.5時阻力系數減小到2.55。

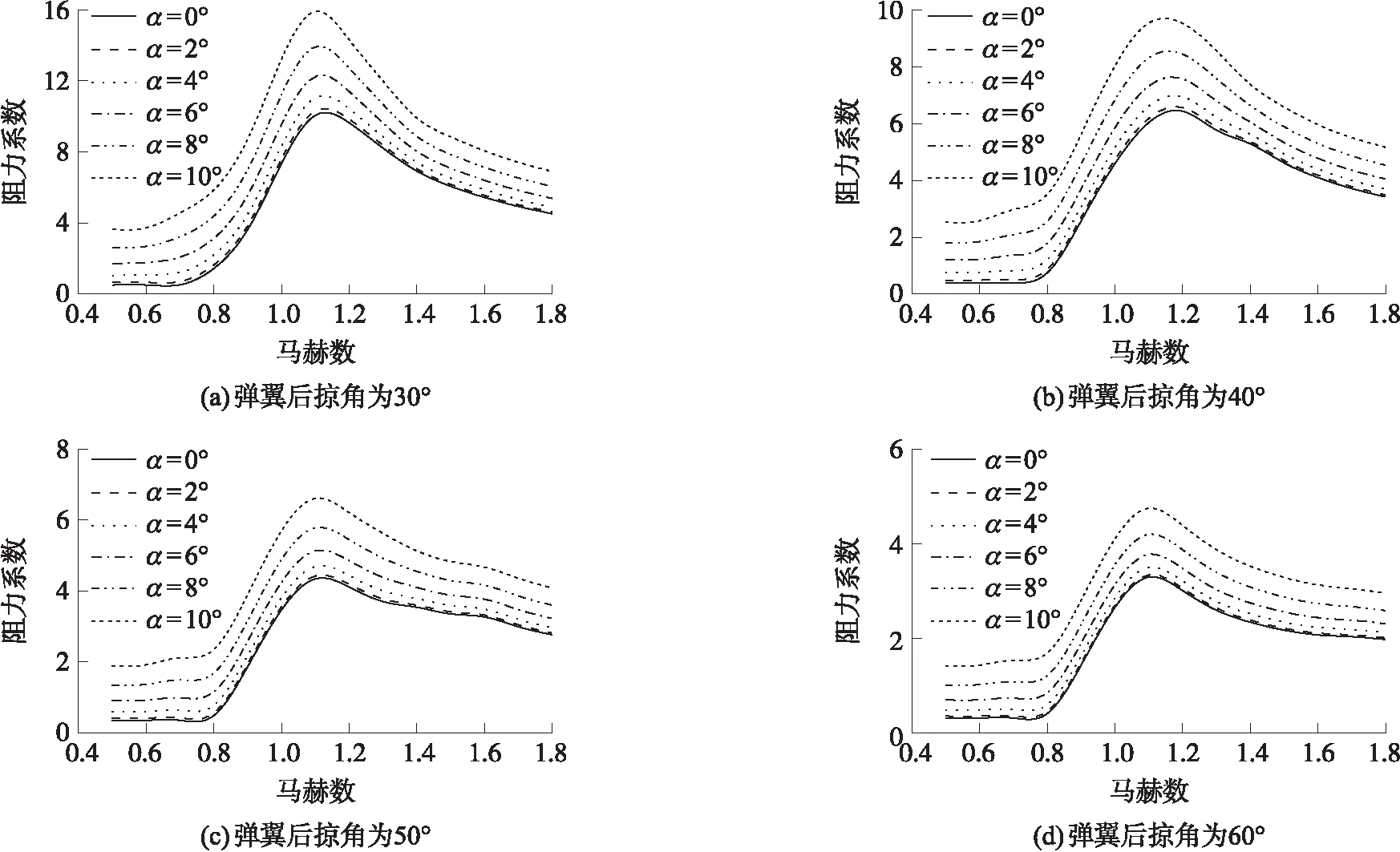
圖4 不同彈翼后掠角時炮彈阻力系數變化Fig.4 Variation of drag coefficient with different sweep angles

如圖5所示,彈翼后掠角的變化對炮彈升阻比影響較大。炮彈飛行馬赫數在1.1以上時,60°后掠角外形的升阻比最大,最高可以達到1.73;隨著飛行速度的減小,50°后掠角外形更具優勢,在馬赫數為0.8和0.9時其升阻比分別達到5.63和2.94,相比60°后掠角外形高出6.9%～12.5%;當炮彈飛行馬赫數降低至0.7及以下時,30°后掠角外形的升阻比最大,最高可達8.36。因此隨著飛行速度的減小彈翼后掠角應該變小,使得彈翼展長和面積增大以提高升阻比,可以以此作為變體制導炮彈飛行過程中變體方案的設計依據。

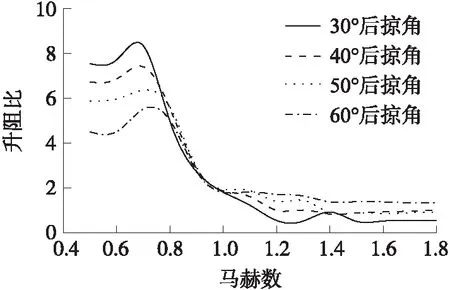
圖5 不同外形最大升阻比隨馬赫數變化Fig.5 Varialion of maximum lift-drag ratio with Ma number

2.2 靜穩定度分析

炮彈靜穩定度的計算表達式如下:

(1)

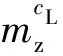
對于變體制導炮彈而言,在火箭發動機工作完成后的上升段彈道,此時鴨舵和彈翼未張開,應提高靜穩定度;在鴨舵和彈翼張開后的有控飛行段,即遠程滑翔段彈道,應減小靜穩定度,以保證良好的操縱性。

如圖6所示,火箭發動機完成工作后炮彈的靜穩定度保持在4%～21%之間,并隨馬赫數減小而增大,滿足上升段穩定性要求。

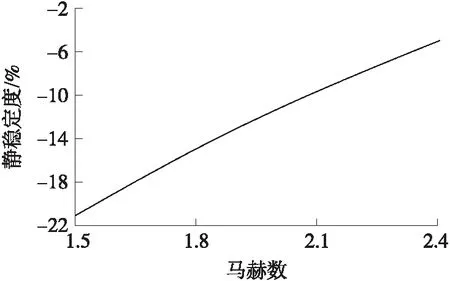
圖6 上升段靜穩定度變化曲線Fig.6 Curve of static stability in ascending stage

變體制導炮彈不同外形靜穩定度隨馬赫數和攻角的變化規律如圖7所示,可知變體制導炮彈不同外形在不同飛行速度的靜穩定度始終保持在0.1%～6.5%之間,在整個滑翔飛行過程中滿足要求。

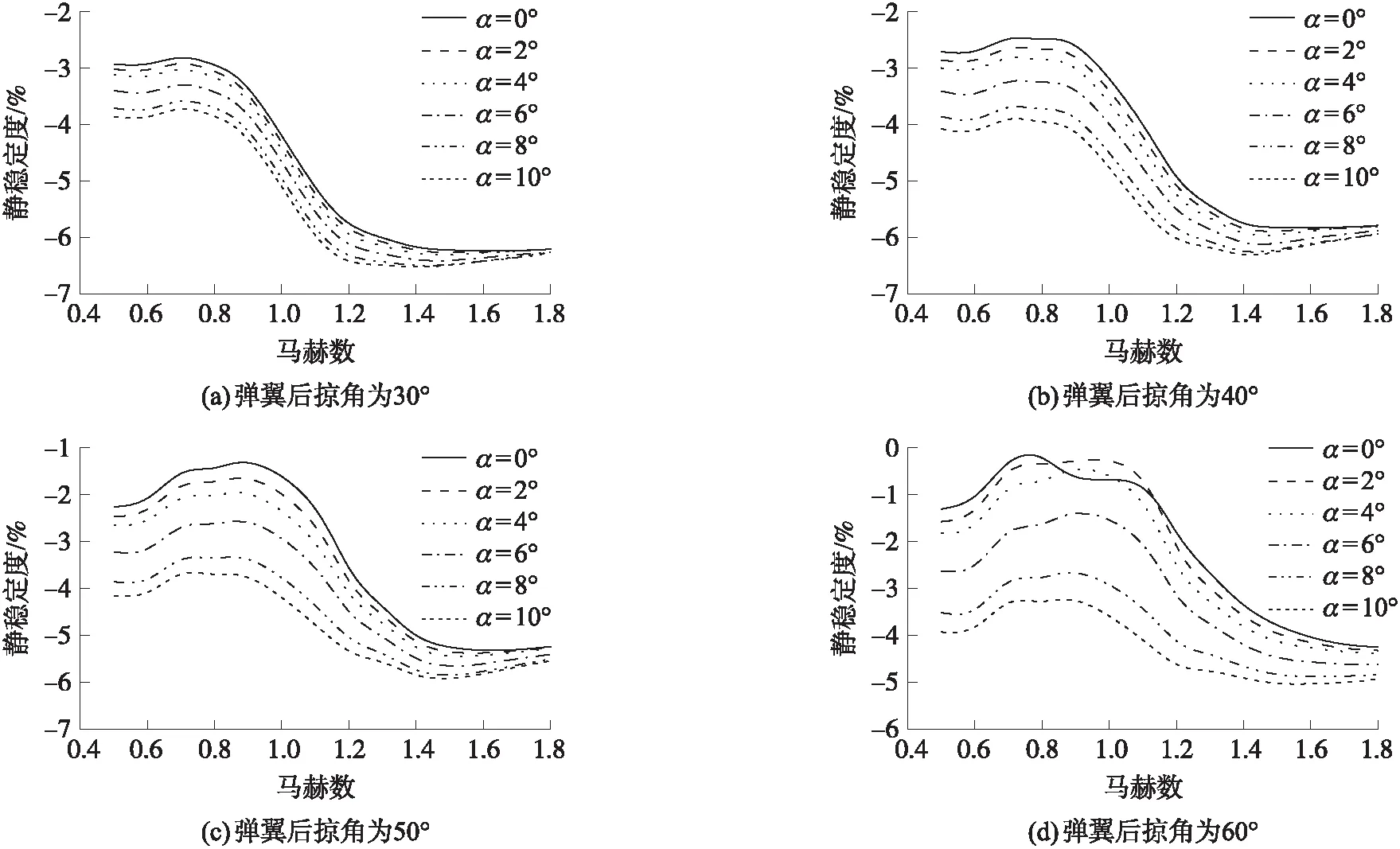
圖7 變體制導炮彈不同外形時靜穩定度變化Fig.7 Curve of static stability of morphing guided projectile with different shape

2.3 操縱特性分析

假設制導炮彈在飛行過程中都處于瞬時平衡狀態,即

(2)

攻角α和舵偏角δ之間的關系可以由下式求得,得到制導炮彈的操縱比:

(3)

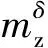
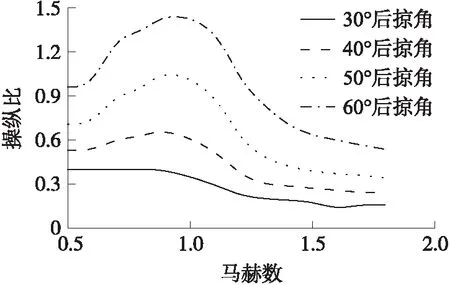
圖8 舵偏角5°時不同外形操縱比隨馬赫數變化Fig.8 Variation of steering ratio with Mach number fordifferent shapes when the canard deflection angle is 5°

3 變體制導炮彈彈道規劃及仿真

3.1 變體制導炮彈變體方案

為了優化變體制導炮彈在飛行過程中的氣動性能,需要制定合適的變體策略以充分發揮變體制導炮彈的優勢。根據前文后掠角對炮彈升阻比影響的分析可知,在剛開始滑翔飛行時,制導炮彈速度較高,此時采用60°后掠角外形升阻比最大;隨著炮彈飛行馬赫數減小至1.1后,彈翼后掠角應該減小至50°以獲得更大的升阻比;在炮彈飛行馬赫速降低至0.7以下時,采用30°后掠角外形飛行,這樣可以保證炮彈在整個滑翔飛行過程中升阻比較大。基于此方案對變體制導炮彈的滑翔段彈道進行優化設計。

表1 變體制導炮彈變體方案Table 1 Morphing scheme of morphing guided projectile

3.2 變體制導炮彈彈道優化模型

為準確描述變體制導炮彈滑翔時的位置和姿態信息,對其受力情況進行簡化:①僅考慮炮彈在縱向平面內的運動;②并且忽略彈翼后掠角變化引起的炮彈質心位置的改變;③將變體制導炮彈看成一個可操控的質點。在此基礎上,建立其在滑翔段的質心運動方程組:

(4)

式中:x為射程,y為射高;v為炮彈的速度;θ為彈道傾角;S為參考面積;ρ為空氣密度;α為攻角;δ為舵偏角;CD和CL分別為全彈的阻力系數和升力系數。

優化問題的本質是在滿足動態約束、路徑約束、邊界約束的前提下尋求最優控制方式u(t),使得性能指標J在從一個狀態轉移到另一個狀態時最小(或最大)的非線性最優控制問題(Optimal Control Problems,OCP),可用Bolza模型描述:

(5)

式中:x(t)∈Rn為n維狀態向量;u(t)∈Rr為r維控制向量;J∈R是性能指標;Φ為Mayer型代價函數;g為Lagrange型代價函數;φ為邊界約束;c為狀態轉移過程中參數約束。根據變制導炮彈彈道優化問題對模型中的參數和約束進行具體定義。

由彈道方程可知,炮彈在飛行過程中的狀態主要由速度、彈道傾角、射程、射高和攻角決定,選取這些變量作為狀態變量。對各種狀態變量的約束稱為狀態約束,在滑翔彈道起點和終點處的約束稱為端點約束。

對速度和彈道傾角在落點處加以約束以確保對目標的毀傷效果:

(6)

在炮彈飛行過程中為保證彈道的平滑和良好的飛行性能,控制變量也受到限制,即:

δ≤|δmax|

(7)

本文設計的變體制導炮彈主要目標是增程,故彈道優化的目的是使其射程最大化,即射程負值極小的問題:

minJ=-x(tf)

(8)

3.3 最優控制問題轉換

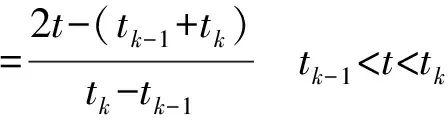
(9)

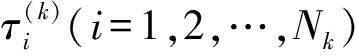
設Li(τ)=(i=1,2,…,N(k))為N(k)階Lagrange插值多項式,即

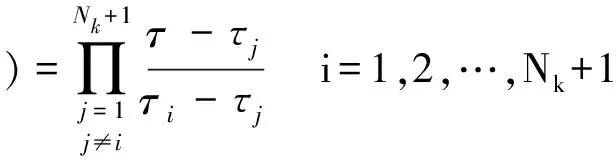
(10)

對狀態變量和控制變量的近似可以采用上式,這樣連續最優控制問題就被離散轉換為多區間NLP問題。

轉化后的NLP問題可以由非線性規劃算法求解,可以增加近似多項式的維數或者增加子區間數,來更新NLP問題,在降低計算量的同時最大限度保證精度要求。

選取狀態軌跡的曲率作為提高求解精度方式的判別準則,當某區間的誤差過大時,若各采樣點的曲率都符合標準,該區間內狀態軌跡平滑,曲率具有一致性,采取增加區間內插值多項式的維數來提高求解精度;否則認為該區間內曲率具有非一致形式,區間狀態軌跡相對來說是非平滑的,此時為提高求解精度需進一步細化區間。

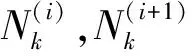
(11)

式中:N(+)為新增加的配點數。

為了細化區間,需要計算得到曲率與曲率平均值的比值,增加子區間的網點位置就是比值最大時對應的采樣點;在每個新增加的區間內,每次新增配點數為N(0)(大小由實際情況決定)。

3.4 變體制導炮彈彈道仿真

基于hp-自適應偽譜法分別對變體制導炮彈以及固定外形制導炮彈以射程最大為目標進行優化,仿真的初始條件如下:v0=800 m/s,θ0=55°,m=100 kg,參考面積S=0.018 87 m2,在出炮口后的5～30 s內火箭發動機工作,推力為2 400 N/s。

飛行過程中彈道、速度、攻角、彈道傾角、舵偏角等的變化規律如圖9～圖14所示。

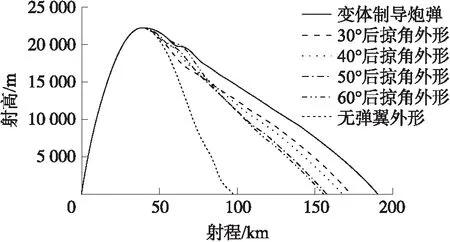
圖9 彈道曲線Fig.9 Curve of trajectory

如圖9所示,無論是變體制導炮彈還是固定外形制導炮彈,彈道軌跡都比較平滑。固定外形制導炮彈最終射程達到155.5～173 km,變體制導炮彈彈翼外形根據變體方案隨飛行速度變化,在飛行過程中保持氣動特性較優,獲得了更大的升阻比,使其滑翔能力更強,最終射程可以達到190.5 km,相比固定外形制導炮彈提高了10.1%～22.5%。

如圖10所示,小后掠角彈翼外形對應更大的展弦比和翼面積,在超音速階段所受阻力也更大,因此后掠角越小,速度衰減越快,而變體制導炮彈在超音速時采用大后掠角外形速度衰減較慢,保留了較大的存速,在亞音速滑翔飛行段更有優勢。同時由于對終點速度的限制,不同外形最終的速度均為160 m/s。

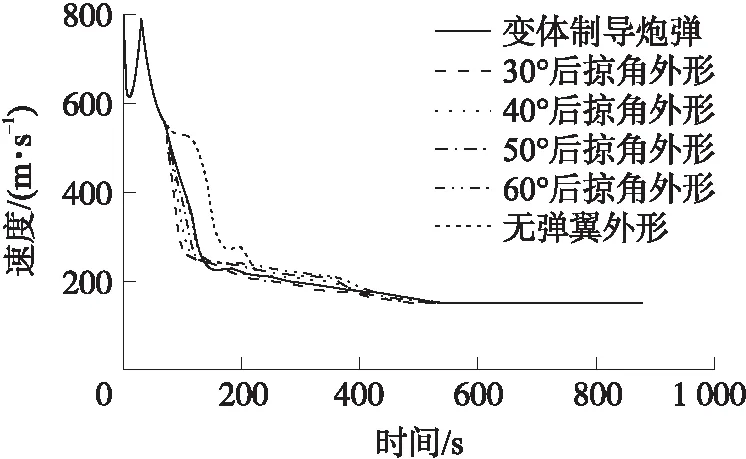
圖10 速度變化曲線Fig.10 Curve of velocity

如圖11所示,由于變體制導炮彈操縱比隨后掠角的增大而增大,所以在操縱機構執行能力有限,即鴨舵最大舵偏角受到限制時,同樣的舵偏角大后掠角外形對應的平衡攻角更大,小后掠角外形則較小。從圖中可以看出,跨音速飛行段大后掠角外形出現了攻角過大的情況,變體制導炮彈在跨音速段通過改變彈翼外形可以避免攻角過大,同時在亞音速滑翔時攻角也保持較小范圍內。

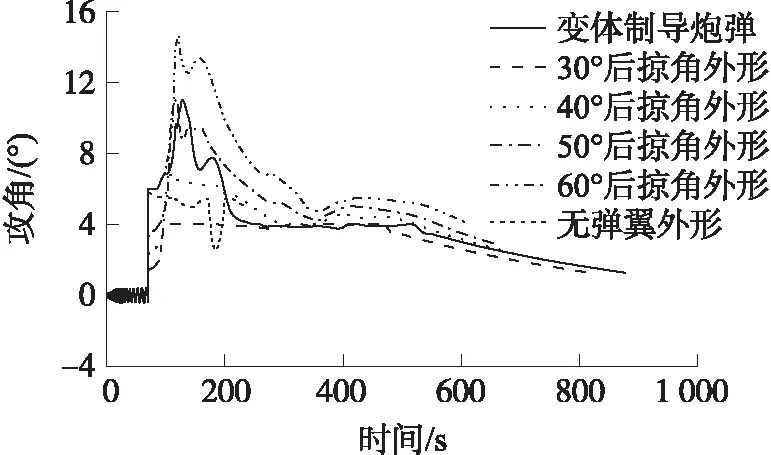
圖11 攻角變化曲線Fig.11 Curve of attack angle

如圖12所示,變體制導炮彈的彈道傾角相比固定外形制導炮彈變化幅度更小,整體變化更加平緩。

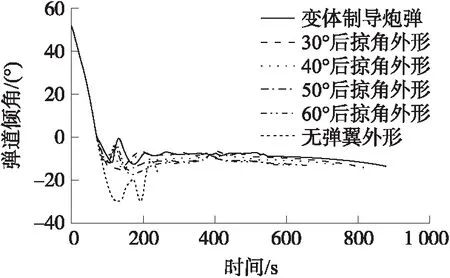
圖12 彈道傾角變化曲線Fig.12 Curve of trajectory inclination

如圖13所示,變體制導炮彈為了獲得更大的升阻比提高滑翔能力,在不同彈翼外形時都需要保持較大的舵偏角來獲得更大的平衡攻角,在整個飛行過程中舵偏角與其他固定外形制導炮彈相比較大。

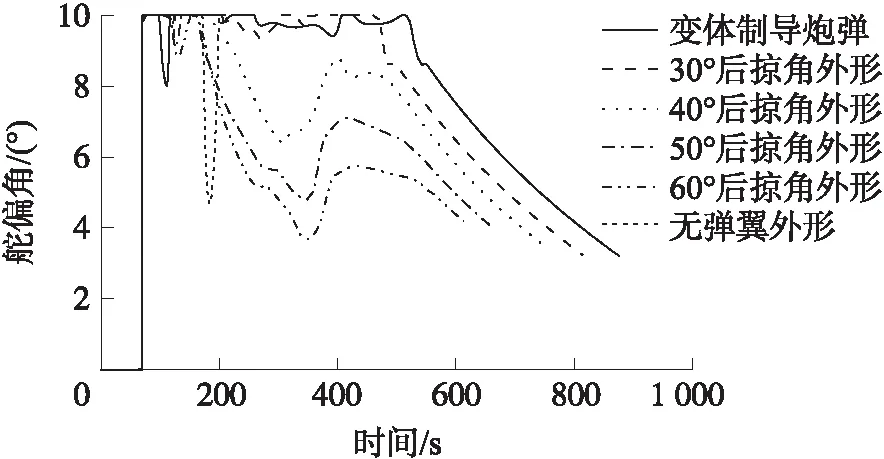
圖13 舵偏角變化曲線Fig.13 Curve of canard deflection angle

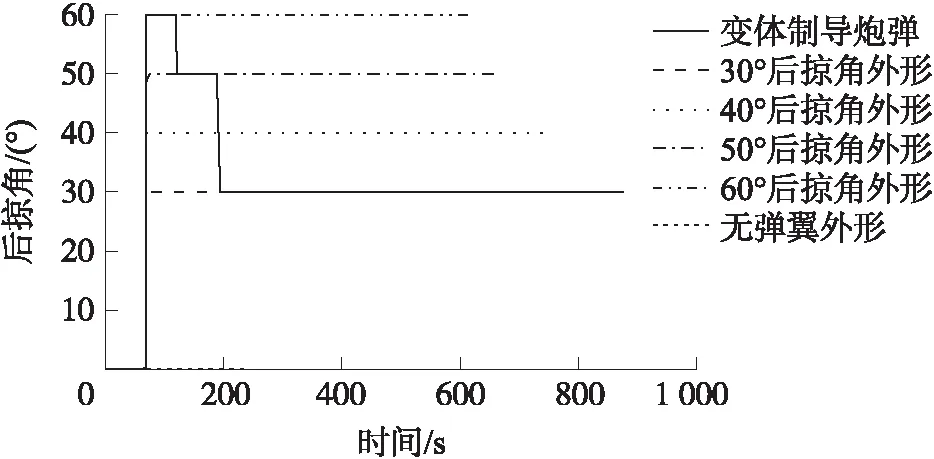
圖14 彈翼后掠角變化曲線Fig.14 Curve of sweep angle

4 結論

本文設計了鴨式布局變體制導炮彈的氣動外形及控制方式;計算其氣動數據并且對氣動特性及操縱性進行分析;基于氣動特性分析的結果規劃了滑翔段飛行時的變體方案,采用hp-自適應偽譜法以射程最遠為目標對變體制導炮彈和固定外形制導炮彈的滑翔段彈道進行優化,仿真結果表明:

①所設計的變體制導炮彈具有良好的氣動特性和操縱特性。

②后掠角變化能夠改善變體制導炮彈在滑翔段的氣動特性,通過改變彈翼外形可以使變體制導炮彈在滑翔飛行過程中保持較優的氣動特性。

③與固定外形制導炮彈相比,變體制導炮彈射程更遠,增幅可達10.1%～22.5%,最遠達到190.5 km。

④變體制導炮彈在超音速飛行過程中速度衰減更慢,滑翔飛行時攻角和彈道傾角波動更小,結果可為變體制導炮彈以后的研究提供參考。