彈性介質中多孔石墨烯增強復合材料截錐殼的振動

黃小林,李糧杰,張燕寧,郝稀奇

(桂林電子科技大學 建筑與交通工程學院，廣西 桂林 541004)

0 引言

石墨烯以其高強、輕質的特性成為優異的增強材料[1]。將石墨烯納米片沿基體材料某一個或多個方向連續梯度分布而制成的功能梯度石墨烯增強復合材料(functionally graded graphene platelets,FG-GPLs)，在航空航天、機械、交通、土木工程等領域有廣闊的應用前景。因此，近年來，對FG-GPLs結構力學特性的研究受到了極大關注[2-5]。

文獻[6]用有限單元法研究了熱環境下FG-GPLs層合板/殼的振動響應，發現熱荷載會引起結構應變畸變，進而影響其固有頻率。文獻[7]通過微分求積法，分析了不同邊界條件下FG-GPLs圓柱殼和環形板的自由振動和靜力彎曲，提出了當石墨烯納米片的長寬比和長厚比處于一定范圍時，可忽略其形狀對結構剛度的影響。文獻[8]基于一階剪切變形理論，建立了FG-GPLs截錐中厚殼的振動方程，研究了石墨烯分布模式和質量分數對結構非線性振動的影響。

由于制造工藝的缺陷，在制備FG-GPLs結構過程中不可避免會產生孔隙，因此，研究含孔隙結構的FG-GPLs的動力學特性很有必要。文獻[9]考慮了含內部孔隙的FG-GPLs梁的振動響應和彈性屈曲行為，提出了高斯隨機場下多孔結構的力學模型，建立了泊松比和孔隙的對應關系。根據開孔泡沫金屬模型，文獻[10]用伽遼金(Galerkin)法和四階龍格庫塔法研究了彈性地基上多孔FG-GPLs板的非線性振動和動態屈曲問題，并通過試驗確定了孔隙對板結構的影響規律。文獻[11]基于克希霍夫-拉夫(Kirchhoff-Love)殼體理論，用瑞麗里茲(Rayleigh-Ritz)法研究了FG-GPLs圓柱殼的自由振動，發現邊界條件和孔隙同時對殼體的力學響應有顯著影響。文獻[12]以虛擬彈簧剛度模擬同邊界條件，基于一階剪切變形理論計算了外部激勵下FG-GPLs圓柱殼的受迫振動，提出了剛度阻尼因數比質量阻尼因數對動撓度幅值的影響更大。文獻[13-14]分別用傅里葉微分求積和廣義微分求積法計算了多孔FG-GPLs截錐殼的固有頻率，發現殼體厚度與固有頻率近似線性相關，而且孔隙對固有頻率的影響不可忽略。

可見，目前關于FG-GPLs構件力學行為的研究中，對板/梁結構研究的較多[15-17]，而對圓錐殼特別是含孔隙的圓錐殼的研究則較少。這是因為，一方面，圓錐殼的靜/動力平衡方程為變系數的高階偏微分方程，求解困難;另一方面，含孔隙的石墨烯增強功能梯度材料物性參數的計算方法比較復雜，不易理解。因此，本文先假定孔隙的體積組分，基于傳統多孔材料物性參數的模型計算FG-GPLs材料的物性參數。然后，考慮周圍彈性介質的影響，建立彈性介質中FG-GPLs截錐殼振動的控制方程并求解。最后，詳細討論孔隙、石墨烯、彈性介質等因素對振動頻率和動力響應的影響，為此類結構的優化提供理論基礎。

1 截錐殼模型物性參數

彈性介質中的截錐殼如圖1所示，彈性介質中含內部孔隙的石墨烯增強材料(FG-GPLs)截錐殼受橫向動荷載q(s,θ,t)作用。殼體厚度和母線長度分別為h和L，截錐殼的小頭半徑、大頭半徑和半錐角分別為R1、R2和γ，s、θ和z方向的中面位移分別為u、v和w,頂點到截錐殼上端和下端的距離分別為S1和S2，彈性介質的壓縮剛度和剪切剛度分別為Kw和Kp。假設截錐殼由基體材料和增強相石墨烯納米片組成。石墨烯納米片和內部孔隙在殼厚度方向均連續分布。圖2為孔隙的分布類型。孔隙分布歸納為4種類型：(a)T1為離中面越遠孔隙越少的對稱分布；(b)T2為離中面越遠孔隙越多的對稱分布；(c)T3均勻分布；(d)T4為從內側到外側孔隙越來越少的分布。

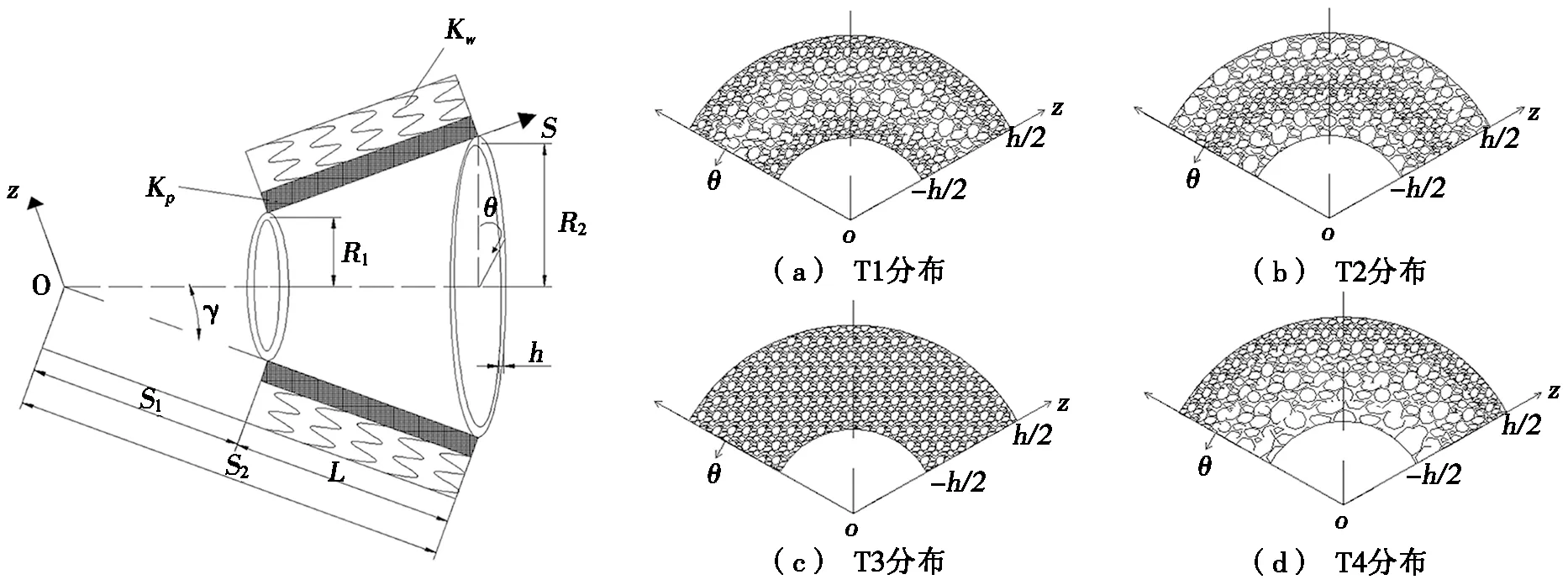
圖1 彈性介質中的截錐殼 圖2 孔隙的分布類型

設孔隙的體積組分沿厚度的分布為[10]:

(1)

其中:e0，e1，α和e2分別為T1,T2,T3和T4分布的孔隙系數。

此截錐殼的彈性模量、剪切模量和泊松比用混合律可表示為:

E(z)=E0(1-VP);

(2)

G(z)=G0(1-VP);

(3)

v(z)=v0(1-VP),

(4)

其中：E0，G0和v0分別為無孔隙時截錐殼的楊氏彈性模量(Pa)、剪切模量(Pa)和泊松比。

假設質量密度為：

(5)

其中：ρ0為不含內部孔隙的石墨烯增強截頂圓錐殼的的密度；em0，em1，α′和em2為質量密度系數。

(6)

從式(6)可看出：給定孔隙體積的分布系數e0，e1，α和e2，可分別計算質量密度的孔隙系數度em0，em1，α′和em2。

假設各種孔隙分布板的質量相同，有：

(7)

根據修正的Halpin-Tsai細觀模型，無孔隙的FG-GPLs截錐殼的有效彈性模量可表示為:

(8)

其中:Em為基體材料的彈性模量；VGPL為石墨烯的體積組分；ξL,ξW,ηL和ηW定義為:

(9)

無孔隙的FG-GPLs截錐殼的泊松比和密度用混合律可表示為:

ν0=νGPLVGPL+νm(1-VGPL)，ρ0=ρGPLVGPL+ρm(1-VGPL),

(10)

其中：ρGPL和νGPL分別為石墨烯的質量密度和泊松比；ρm和νm分別為基體材料的質量密度和泊松比。

無孔隙的FG-GPLs截錐殼的剪切模量為:

(11)

假設石墨烯沿殼厚度有3種分布類型(見圖3)。其中，(a)G1為石墨烯數量由內、外側向中面逐漸減少的分布。反過來，(b)G2為內、外側向中面逐漸增大的分布。而(c)G3為均勻分布。3種分布石墨烯的體積組分VGPL假設為：

(a) G1分布 (b) G2分布 (c) G3分布

(12)

其中：Vi1,Vi2和Vi3分別為G1，G2和G3石墨烯分布下體積分數的最大值。

設3種分布類型的石墨烯總體積分數相等，則有如下關系式：

(13)

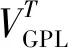
(14)

2 振動方程及求解

假設截錐殼在變形過程中始終與彈性介質緊密接觸，且忽略其阻尼與慣性力的作用，則彈性介質對截錐殼的反作用力為[18]：

(15)

引入變量φ=θsin(γ)和應力函數F。應力函數與面內力的關系為：

(16)

令s=S1ex,F=F1e2x，基于Donnell經典薄殼理論和Hamilton原理，可推導此截錐殼振動的控制方程為：

(17)

L21(F1)+L22(w)=0,

(18)

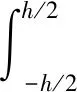
設截錐殼的邊界條件為兩端簡支，其動撓度的形式解為：

(19)

(20)

其中：系數Ki見文獻[18]，再將式(19)和式(20)代入式(17)，兩邊同乘以exsin(m1x)sin(n1φ),得：

(21)

其中：W={W11,W12,...Wm1,n1...}T為動撓度列向量，M和K分別為質量矩陣和剛度矩陣；q={q11,q12,...qm1,n1...}T為荷載列向量，且:

(22)

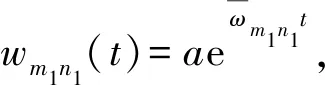
det(ω2M+K)=0。

(23)

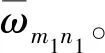
當q(x,φ,t)≠0時，用Newmark數值積分法可求得其動撓度。本文采用的Newmark積分法的2個計算參數分為β=0.5，γ=0.25，時間步長Δt=0.001s。

3 比較算例和參數分析

表1計算了彈性介質中純金屬功能梯度材料(functionally graded materials，FGM)截錐殼的量綱歸一化頻率。基體材料鎳和增強材料陶瓷的物性參數見表2。增強材料的體積分數在厚度的分布為:

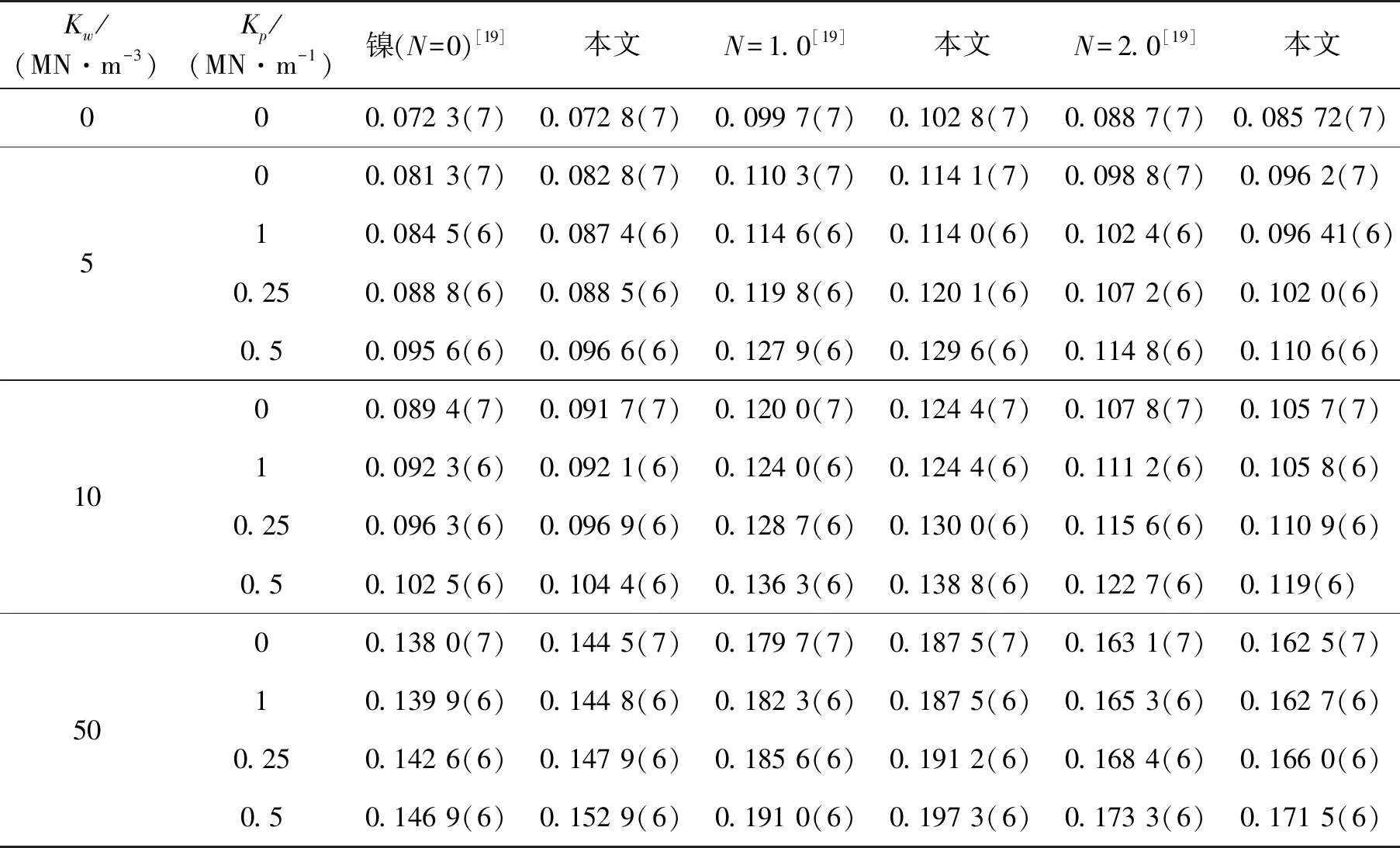
表1 彈性介質中純金屬功能梯度材料截錐殼的量綱歸一化頻率

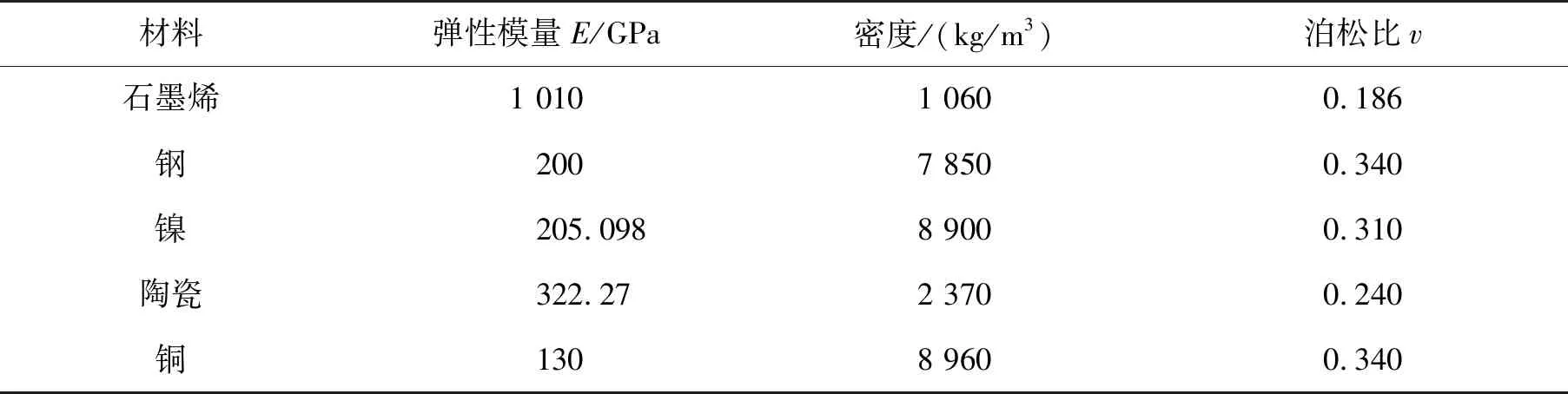
表2 材料物性參數

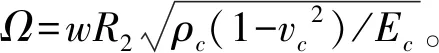
表3計算了含孔隙的石墨烯增強復合材料(FG-GPLs)圓柱殼的固有頻率。當半錐角γ→0時，S1→∞，S1sinγ=R，S2=S1+L，x0=L/S1時，截錐殼退化為圓柱殼。殼體基體材料為鋼，石墨烯納米片的幾何尺寸為長aGPL=2.5×10-9m，寬bGPL=1.5×10-9m，厚hGPL=1.5×10-6m，圓柱殼柱殼尺寸R=1 m，L/R=20，h=0.002R，石墨烯質量分數WGPL=1.0%。

表3 含孔隙的FG-GPLs圓柱殼的固有頻率 Hz

由表1和表3可看出：本文的計算結果和相關文獻的結果是比較接近的。

表4和表5列出了不同孔隙分布和石墨烯分布、不同孔隙系數和彈性介質參數下截錐殼的量綱歸一化頻率。從表4和表5中可看出：4種孔隙類型的量綱歸一化頻率均隨孔隙系數e0的增大而減小，而且T1分布的量綱歸一化頻率比其他3種分布都大，說明在4種孔隙分布中，T1分布對截錐殼整體剛度的削弱程度最小。在3種石墨烯分布中，G1分布的量綱歸一化頻率最大，G2分布最小，說明按G1分布植入石墨烯納米片更能提高截錐殼的整體剛度。另外，量綱歸一化頻率隨剪切參數Kp及壓縮參數Kw彈性參數的增大而提高，而且兩者比較，剪切參數Kp比壓縮參數Kw提高的程度更為顯著，說明在介質的彈性壓縮和彈性剪切性質中，剪切變形的影響程度更大。例如，在孔隙分布和石墨烯分布為T1和G1，e0=0.1時，Kw從0增大到1.0，量綱歸一化頻率只提高5%。而Kp從0只增大到0.1時，量綱歸一化頻率卻提高了7.6%。

表4 T1和T2孔隙分布下FG-GPLs截錐殼的量綱歸一化頻率

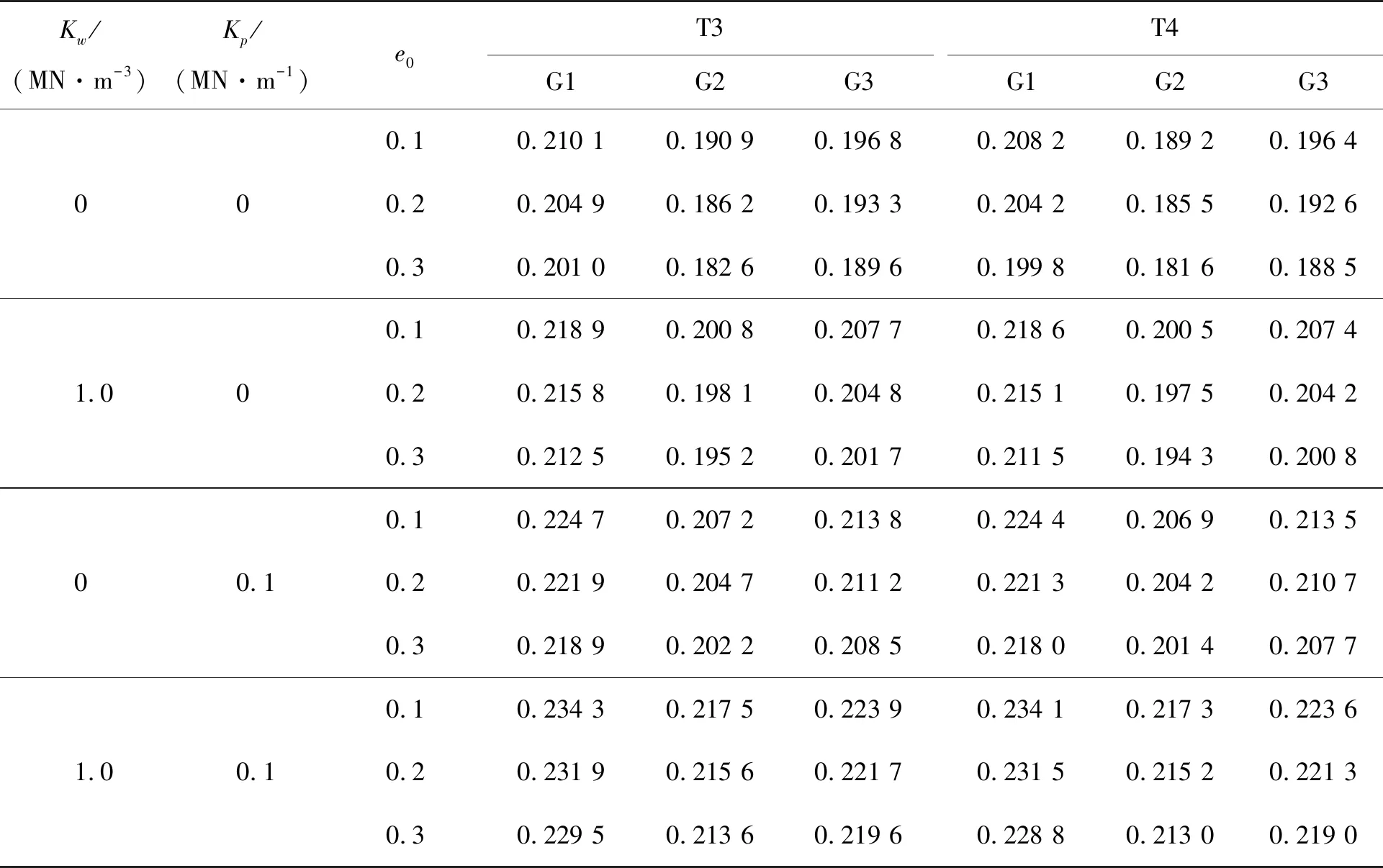
表5 T3和T4孔隙分布下FG-GPLs截錐殼的量綱歸一化頻率

圖4為T1和T3孔隙分布的量綱歸一化頻率Ω隨石墨烯質量分數的變化曲線。由圖11可看出：Ω隨著石墨烯質量分數WGPL的提高而增大，而且WGPL越大，Ω的增長越快。以T1/G1為例，當WGPL=1.0%時，Ω約提高20.51%，說明添加少量石墨烯納米片能顯著提高截錐殼的整體剛度，這是因為石墨烯的彈性模量遠比基體材料大而質量密度又遠比基體材料小。此外，綜合表4和表5可得：不同石墨烯分布類型的增長速度不同，G1最大而G3最小，再次證實了G1分布能更有效提高材料的整體剛度。

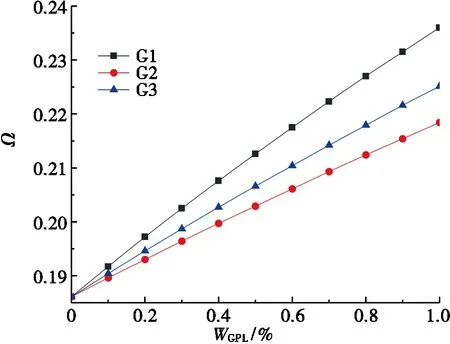
(a) T1分布

圖5～圖7計算了不同彈性介質參數、孔隙系數、石墨烯質量分數下截錐殼的動撓度，其中，橫向動荷載q(s,θ,t)=8 000 sin(500t)Pa,動撓度的坐標點為(S1+L/2,π/2)。

由圖5可看出：動撓度隨彈性介質參數的增大而減小，對T1/G1類型，彈性介質參數(Kw,Kp)=(1,0)比(Kw,Kp)=(0,0)的動撓度幅值約低30.55%，(Kw,Kp)=(0,0.1)比(Kw,Kp)=(0,0)動撓度幅值約低47.37%，可見，同對量綱歸一化頻率一樣，剪切參數Kp比壓縮參數Kw的影響更顯著，印證了介質的剪切參數對圓錐殼有限剛度的影響比壓縮系數大。

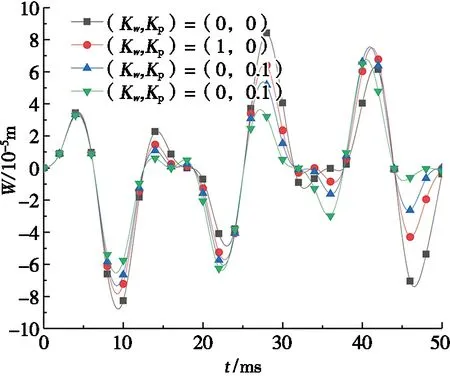
(a) T1/G1

圖6為孔隙系數對截錐殼動撓度的影響。從圖6a中可看到：孔隙系數e0從0.1增大到0.3時，最大動撓度提高約14.7%，這是由于孔隙系數越大，孔隙率越大，圓錐殼的有效剛度變小。而在同為G1石墨烯分布的情況下，當孔隙系數e0=0.3時，T1孔隙分布的最大動撓度比T3分布的最大動撓度只小了8.52%,說明孔隙分布對動撓度的影響并不顯著。

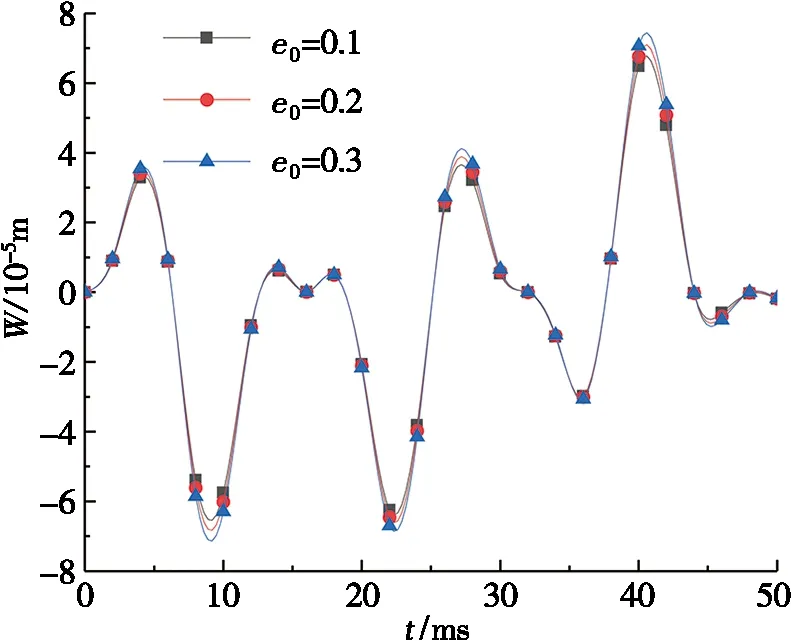
(a) T1/G1

圖7為石墨烯質量分數對截錐殼動撓度的影響。從圖7a和圖7b可知：石墨烯質量分數WGPL從0%提高到0.6%，T1/G1類型的截錐殼的動撓度幅值減少約36.83%，T1/G3動撓度幅值減小約45.66%，石墨烯納米片可顯著提高截錐殼的整體剛度，因此，動撓度幅值隨石墨烯質量分數的提高而明顯減小。

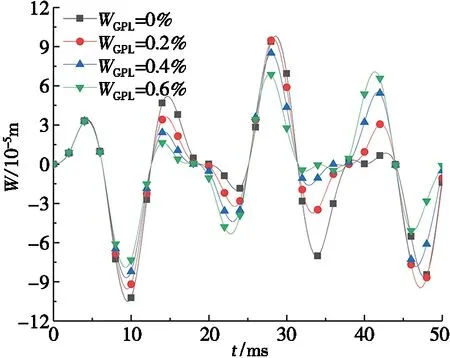
(a) T1/G1

4 結論

(1)與孔隙系數相比，孔隙的分布類型對振動頻率和動力響應的影響更為顯著。由振動頻率的結果可看出，在T1,T2,T3和T4 這4種孔隙分布類型的截錐殼中，T1的整體剛度最大，而T2的整體剛度最小。

(2)在基體材料中植入少量的納米片可顯著提高截錐殼的振動頻率和降低動撓度的幅值，而且不同的石墨烯分布類型，其影響程度不同。在G1,G2和G3這3種石墨烯分布類型中，G1的影響程度最大，而G2最小，故T1孔隙分布和G1石墨烯分布截錐殼的剛度最大。

(3)彈性介質提高了截錐殼的振動頻率，并且降低了動撓度的幅值。與壓縮剛度參數相比，剪切剛度參數的影響更為明顯。