超聲滾擠壓軸承套圈加工參數優化

徐紅玉,付浩然,王曉強,靳園園

(河南科技大學 機電工程學院，河南 洛陽 471003)

0 引言

軸承作為機械裝配的基礎零部件，其使用性能對機械設備的壽命有很大影響。由于軸承長期承受高速動載荷作用，軸承套圈極易發生疲勞破壞，從而影響軸承的綜合性能。為有效提高軸承套圈的表面質量和疲勞壽命，對其進行表面強化具有重要的工程應用價值。

在表面強化領域，超聲滾擠壓作為一種近凈成形強化技術，通過改變表面微觀形貌和增強物理力學性能，從而達到較高的表層性能，近年來國內外學者進行了大量的試驗研究。文獻[1]針對軸承套圈脫碳、尺寸變形、表面燒傷等問題，進行超聲滾壓光整強化加工，來改變軸承套圈的表層性能，進而提高其耐磨損、抗疲勞特性。文獻[2]通過對45鋼表面超聲滾壓加工，由性能測試發現表面粗糙度得到降低，硬度得到提高，顯微組織晶粒進行了細化。文獻[3]通過超聲擠壓45鋼，設計正交試驗分析不同加工參數對表層粗糙度和硬度的影響，并與常規擠壓進行對比，表層性能得到改善。文獻[4]通過利用超聲波振動的機械表面增強技術，對Ti-6Al-4V試樣處理后的試驗結果(如表面粗糙度、表面顯微硬度和壓縮殘余應力)進行評價和比較。文獻[5-7]將超聲滾擠壓技術應用到軸承套圈表面，通過建立表層性能的預測模型，對工藝參數進行優化，進一步改善了軸承套圈表面完整性，延長了軸承使役壽命。文獻[8]基于灰色關聯分析，研究了超聲滾擠壓軸承套圈最優加工參數，并分析了加工參數對表層性能的影響規律，最后通過建立灰色關聯度的預測模型進行了驗證。文獻[9]為提高軸承套圈表層性能進行正交試驗，建立加工參數與表層性能之間的響應曲面模型，采用模擬退火算法對表層性能進行優化，得到最優加工參數組合。文獻[10]研究了超聲噴丸鋁合金表面后的微觀形貌以及物理力學性能改善狀況，表面顯微硬度提高，殘余壓應力以及晶粒細化提高了材料疲勞壽命。文獻[11]通過對激光切割的加工參數進行正交試驗，由極差、方差分析得到表面質量最優時的加工參數組合，并建立反向傳播神經網絡預測模型驗證其可行性。文獻[12]基于泰勒公式建立誤差傳遞的半參數模型，利用最小二乘法進行參數及半參數求解，并將該模型應用于軸承套圈的磨削加工中，進行方差分析和檢驗。文獻[13]針對傳統進化算法收斂速度緩慢、搜索能力差的問題，提出了一種改進的進化學習算法，并進行試驗與傳統進化算法對比，識別度得到顯著提高。

文獻[14]對軸承鋼進行車削試驗，研究工藝參數對性能特征的綜合影響，通過響應面方法對工藝參數和性能特征之間的關系進行建模，并進行多目標優化，找到最優工藝參數值。文獻[15]將熵權理論與灰色理論相結合，研究冷滾打加工參數對花鍵的影響程度，基于灰色關聯度得出最優冷滾打加工參數組合。文獻[16]通過提出改進的鴿群優化算法，引入模糊交叉變異分子增強算法的搜索能力，并與差分進化算法、粒子群算法、傳統鴿群算法進行優化對比，該算法經過測試尋優能力提高了47.73%。文獻[17]通過對車削合金時加工參數的優化，將信噪比與灰色關聯分析結合進行多目標優化，并與基于信噪比的單目標優化進行對比分析。

綜上所述，以上學者在表面強化方面取得了一定的成就，但是對于軸承套圈表層性能的優化分析以及加工參數影響規律研究還較少。本文以42CrMo鋼作為試驗材料進行超聲滾擠壓正交試驗，將田口信噪比與熵權理論結合，探討加工參數對表層性能的影響顯著性以及最優加工參數組合，并通過主效應分析得到各表層性能最優時的加工參數組合和加工參數對表層性能的影響規律。

1 軸承套圈超聲滾擠壓試驗

1.1 試驗原理

超聲滾擠壓是一種將傳統滾擠壓與超聲波結合的近凈成形技術。它是通過超聲波發生器將交流電轉化為振動的電信號，再由換能器與變幅桿的作用，將其轉變為擴大的機械振動，傳遞到滾擠壓工具頭進行加工。此時，滾擠壓工具頭在靜載荷和動載荷雙重作用下，高速撞擊材料表面，使其發生金屬塑性流動，從而改善表面質量。超聲滾擠壓加工原理如圖1所示。

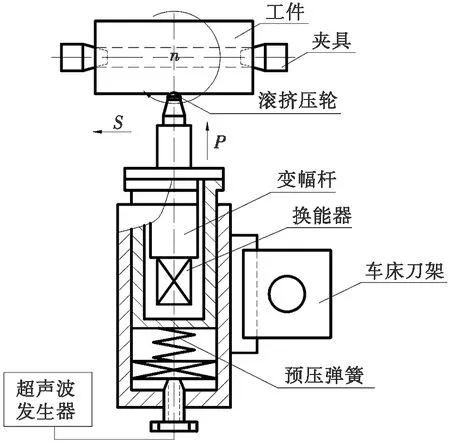
圖1 超聲滾擠壓加工原理圖

1.2 試驗材料及設備

本次采用淬火處理的42CrMo鋼制棒料等效試驗，長度為300 mm，直徑50 mm。為使加工精度更高，超聲滾擠壓試驗是在CKJ6142數控車床上操作的，分別用表面粗糙度輪廓儀、X射線應力儀、維氏硬度儀測量表面粗糙度、殘余應力、硬度。試驗加工過程如圖2所示。

圖2 超聲滾擠壓加工過程

1.3 試驗設計與結果

超聲滾擠壓試驗主要工藝參數：轉速n(r/min)、進給速度f(mm/min)、振幅A(μm)、靜壓力F(N),進行L25(54)正交試驗，水平設置如表1所示，正交試驗結果如表2所示。

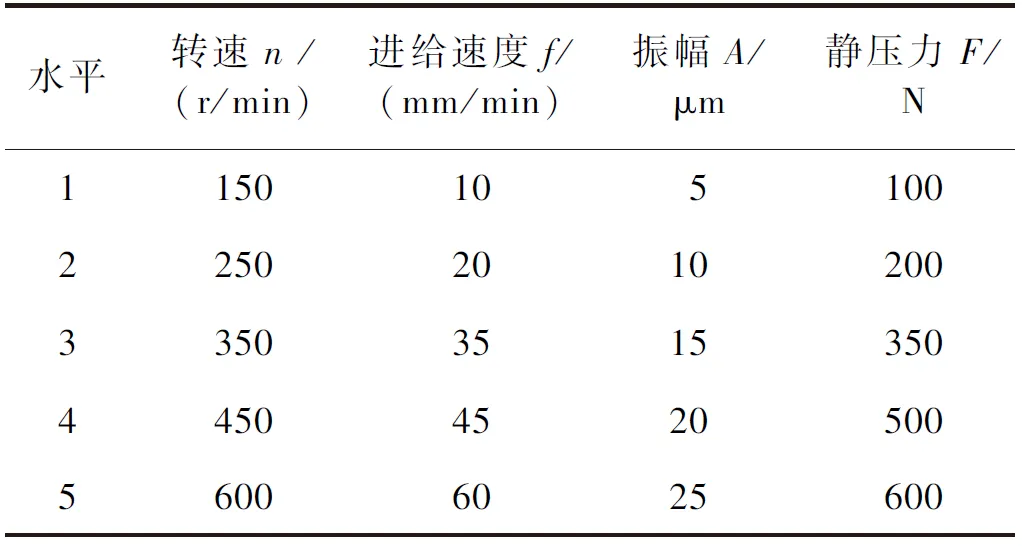
表1 正交試驗工藝參數水平設置

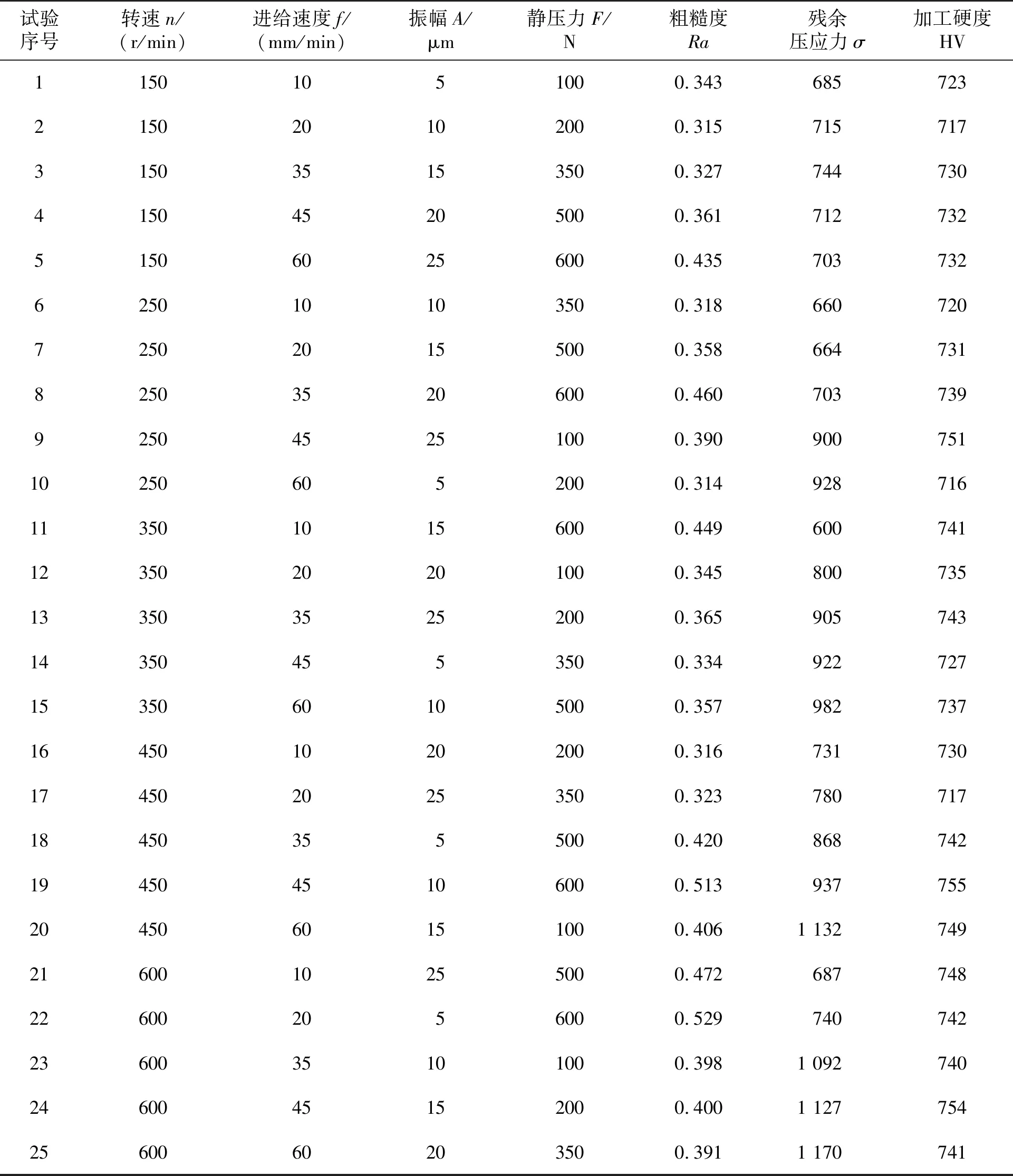
表2 正交試驗結果

2 表層性能預測模型建立

2.1 二階響應回歸模型

二階響應回歸方程通過采用最小二乘法擬合，建立數學回歸理論模型來分析影響因子與結果之間的聯系，具有較強的穩定性[18]。本文以超聲滾擠壓的加工參數為自變量，以軸承套圈的表層性能為因變量，構建二階響應回歸預測模型。表面粗糙度二階回歸方程：

Ra=0.296 7+0.000 893n+0.012f-0.024 77A-0.000 779F-0.000 001n2-0.000 14f2-0.000 661A2+

0.000 001F2-0.000 024nf+0.000 063nA+0.000 588fA-0.000 003fF。

(1)

殘余壓應力二階回歸方程：

σ=633+0.137n+9.09f-18.1A+0.178F-0.000 08n2-0.088 2f2-0.046A2+0.000 427F2+0.002 56nf+

0.051 3nA-0.001 105nF+0.171fA+0.000 87fF-0.024AF。

(2)

加工硬度二階回歸方程：

HV=738.92-0.090 28n+3.737 9f-13.886A+0.221 25F+0.000 057n2-0.039 516f2-

0.055 93A2+0.000 557F2-0.008 256nf+0.040 523nA-0.000 720nF+0.183 75fA-

0.000 672fF+0.019 472AF。

(3)

2.2 預測模型分析

通過擬合方程生成的表面粗糙預測模型殘差圖可以看出，在零點附近數據為隨機分布，如圖3所示。為了得到精度較高的表層性能的預測模型，對二階響應回歸模型進行方差分析，表面粗糙度的相關系數R=98.28%，調整相關系數Radj=98.26%；殘余壓應力的相關系數R=98.46%，調整相關系數Radj=97.69%；加工硬度的相關系數R=98.88%，調整相關系數Radj=98.65%。表面粗糙度、殘余壓應力、加工硬度的P值均小于0.000 1。P為可置信水平，一般小于0.05認為可接受的錯誤水平，P值越小可信度越高，表層性能的P值均小于0.000 1，進一步說明了模型擬合效果較好。

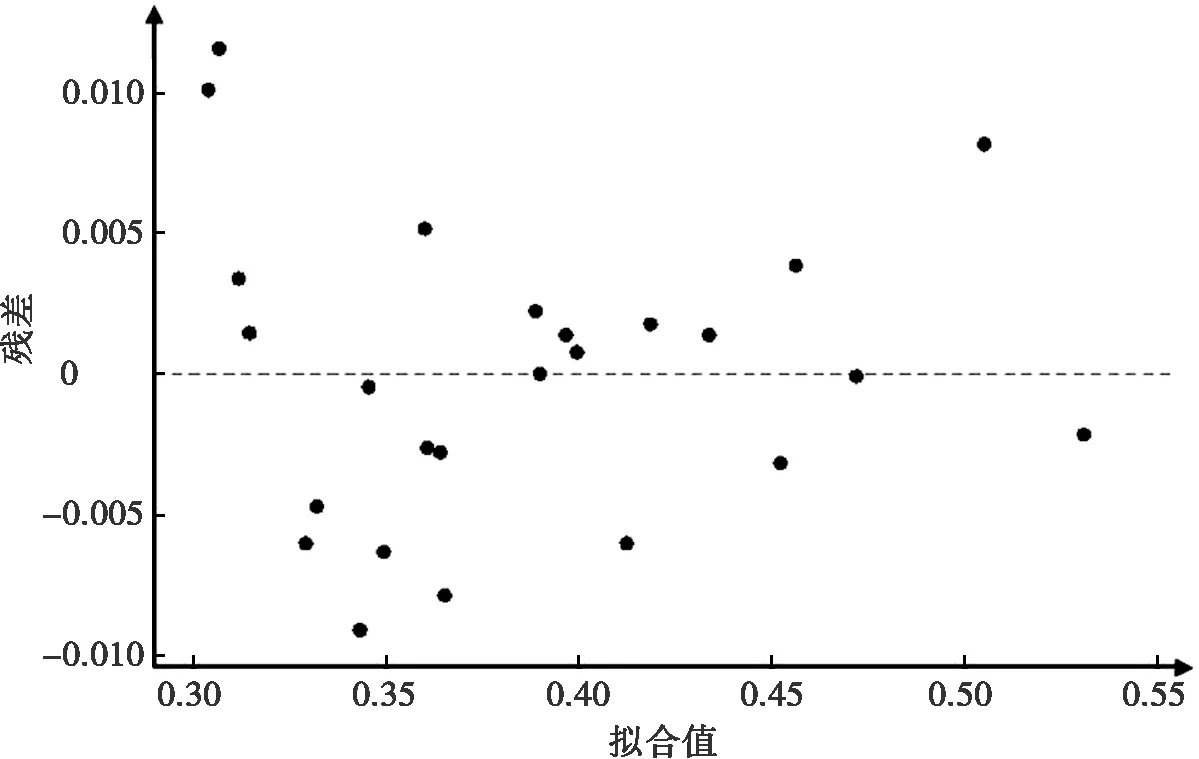
圖3 表面粗糙度預測模型殘差圖

3 超聲滾擠壓加工參數優化及分析

在多目標優化方面，由于各目標在全局分析過程中所占權重不同，因此采用熵權理論[19]對軸承套圈表層性能的權重進行評價，結合田口算法與主效應分析法對超聲滾擠壓加工參數進行綜合分析，研究加工參數對軸承套圈表層性能的顯著性和影響規律，獲得最優加工參數水平。

3.1 基于熵權理論的表層性能權重確立

根據超聲滾擠壓試驗結果建立表層性能的評價矩陣，如式4所示：

(4)

其中:n為表層性能的評價水平；m為評價指標；Dm×n為各水平評價指標的響應值。

將表2試驗結果代入式(4)中，得到表面粗糙度、殘余壓應力、加工硬度的評價矩陣。因評價指標單位各不相同，需要對其進行無量綱化處理。由軸承套圈表層性能特性可知表面粗糙度越小越好，采用式(5)處理；殘余壓應力和加工硬度越大越好，采用式(6)處理。

(5)

(6)

其中：aij為評價矩陣第i行元素;maxaij為評價矩陣第i行中最大值;minaij為評價矩陣第i行中最小值。

經過處理以后得到表層性能的規范矩陣：

根據超聲滾擠壓軸承套圈在生產和實際方面的應用，確定表層性能的主觀熵權，基于規范矩陣通過式(7)～式(10)對主觀熵權進行修正，得到綜合熵權。表層性能熵權計算結果如表3所示。

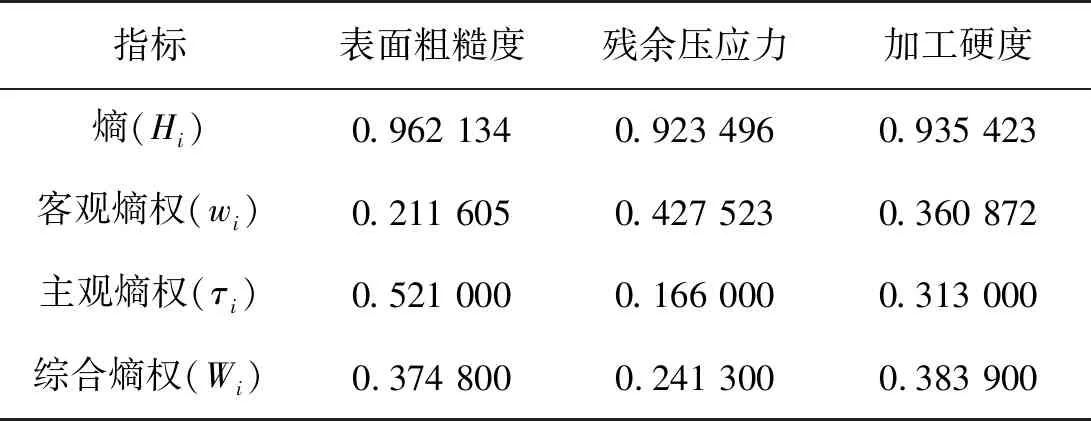
表3 表層性能熵權計算結果

(7)

(8)

(9)

(10)

其中：Lij為第i個指標在第j次時的權重;Hi為第i個指標的熵;ωi為第i個指標的客觀熵權;τi為主觀熵權;Wi為綜合熵權;Lij∈[0,1]，Hi∈[0,1]，ωi∈[0,1]，∑Wi=1。

3.2 基于信噪比的試驗結果分析

由于信噪比[20]能夠對多參數、多目標加工系統進行優化，而且具有簡單、快捷、全局尋優的特點。因此采用信噪比(signal to noise，S/N)作為超聲滾擠壓軸承套圈表層性能分析的評估特征，研究加工參數對表層性能的影響特性。文獻[21]表面粗糙度增大使工件應力集中影響疲勞強度；工件受力產生塑性變形，提高加工硬度能夠抵抗局部變形；殘余壓應力能夠減小工件表面裂紋、改善工件的疲勞強度。對表面粗糙度進行望小處理，殘余壓應力、加工硬度進行望大處理，如式(11)～式(12)所示，處理結果如表4所示。

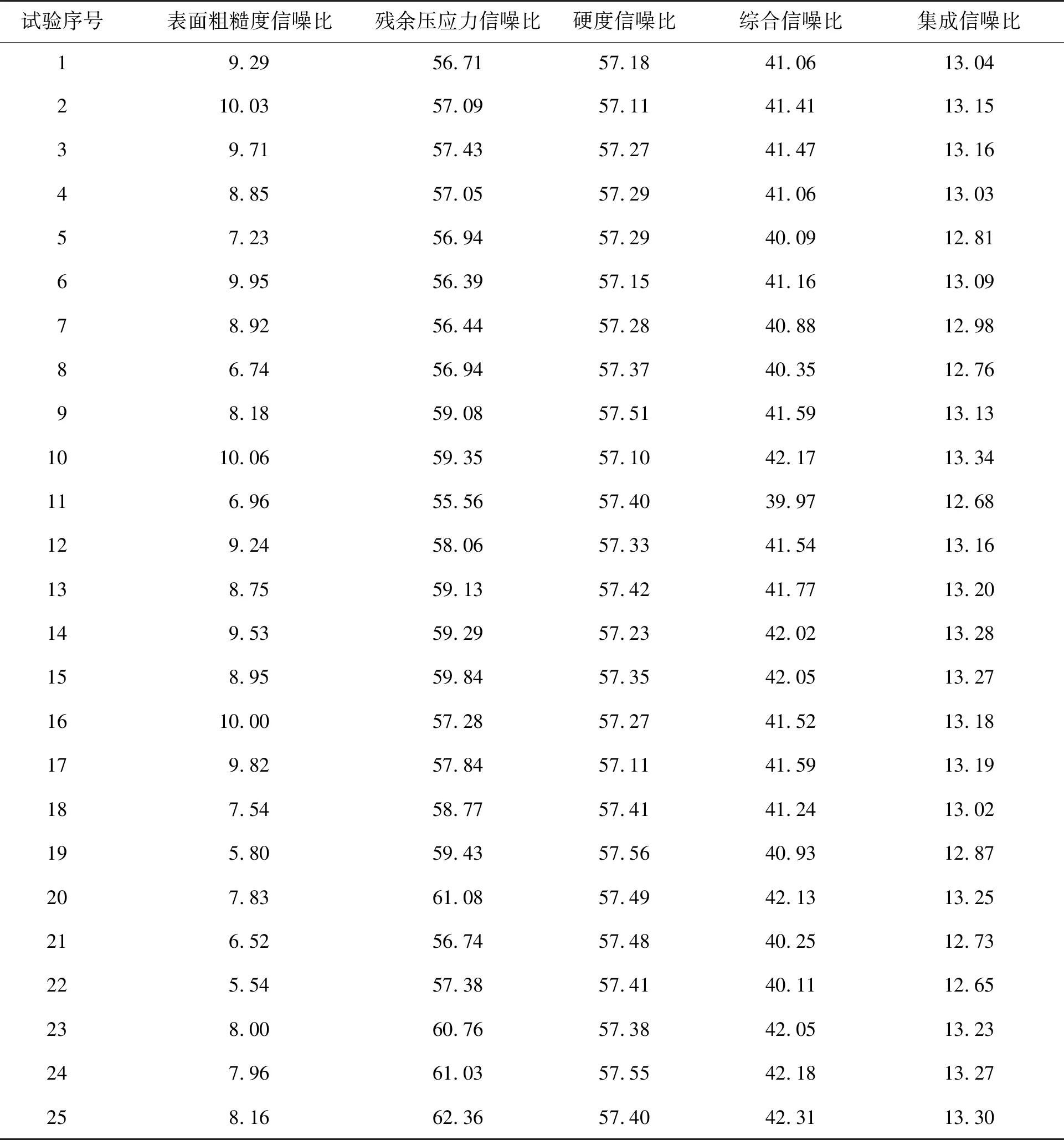
表4 試驗結果信噪比

(11)

(12)

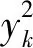
由信噪比基本特性可知，總的差異等于超聲滾擠壓各加工參數的差異與未知差異之和，如式(13)～式(14)所示。超聲滾擠壓試驗中各加工參數的不同水平造成的差異SSL由式(15)計算。將上述計算結果整理得到超聲滾擠壓軸承套圈表層性能的變異系數，如表5所示。

SST=SSn+SSf+SSF+SSA+SSe；

(13)

(14)

(15)

其中：SST為總的差異；SSn、SSf、SSF、SSA分別為超聲滾擠壓加工參數的差異；SSe為未知差異；yi為表層性能的綜合信噪比；G為每組試驗結果綜合信噪比的和；m為試驗次數；t為每個水平的重復次數；Syi2為各加工參數下各水平試驗結果綜合信噪比和的平方。

由變異系數分析估計法知變異系數權重越大，影響越為顯著。由表5得出：靜壓力變異系數權重最大為62.84%，對表層性能影響最為顯著。其次，進給速度變異系數權重為27.49%，對表層性能影響略微顯著。最后，轉速變異系數權重為4.66%，振幅變異系數權重為3.16%，相差不大，對表層性能顯著性較小。綜上，加工參數對軸承套圈表層性能的影響顯著性依次為：靜壓力>進給速度>轉速>振幅。

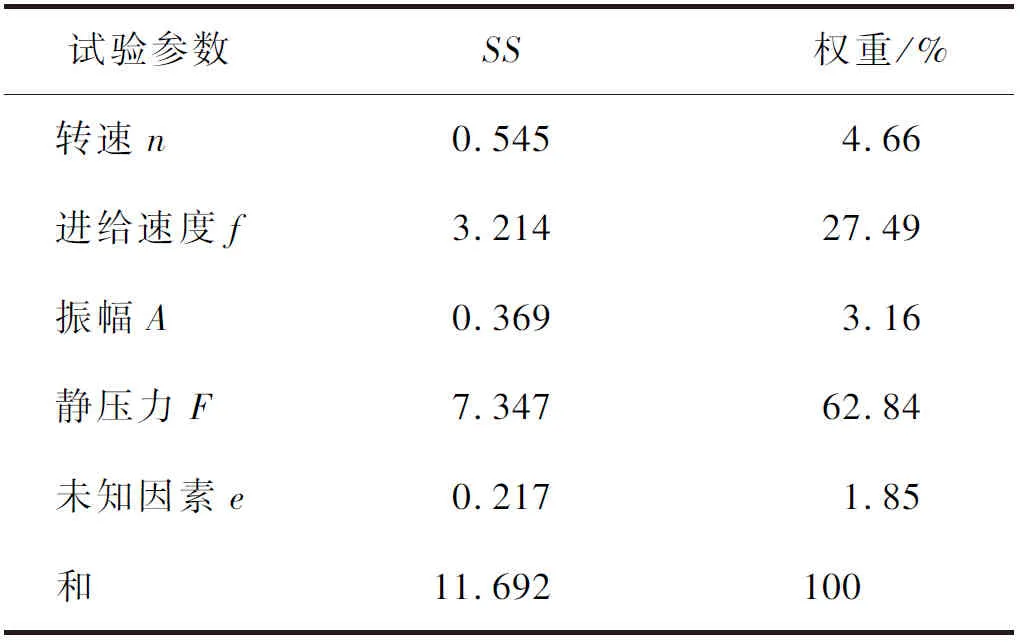
表5 加工參數變異系數分析結果

采用主效應分析法[22]探索超聲滾擠壓加工參數對軸承套圈表層性能的影響規律，表面粗糙度主效應如圖4所示。由圖4可知：隨著轉速增加，Ra逐漸增大。隨著進給速度增加，Ra先減小后增大，接著又呈減小趨勢。隨著振幅增加，Ra先減小后增大，接著又逐漸減小，最后逐漸增大。隨著靜壓力增加，Ra先減小后增大。殘余壓應力主效應如圖5所示，對于殘余壓應力σ：隨著轉速和進給速度增加，σ逐漸增加；隨著振幅的增加，σ先增大后減小；隨著靜壓力增加，σ逐漸減小。如圖6所示，對于加工硬度HV：隨著轉速增加，HV逐漸增大。隨著進給速度增加，HV呈現先減小再增大，最后減小的趨勢。隨著振幅增加，HV呈現先增大再減小最后又增大的趨勢。隨著靜壓力增加，HV先減小后增大。

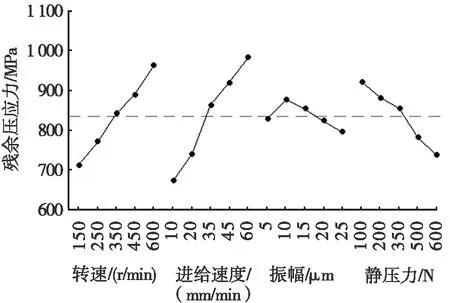
圖5 殘余壓應力主效應圖

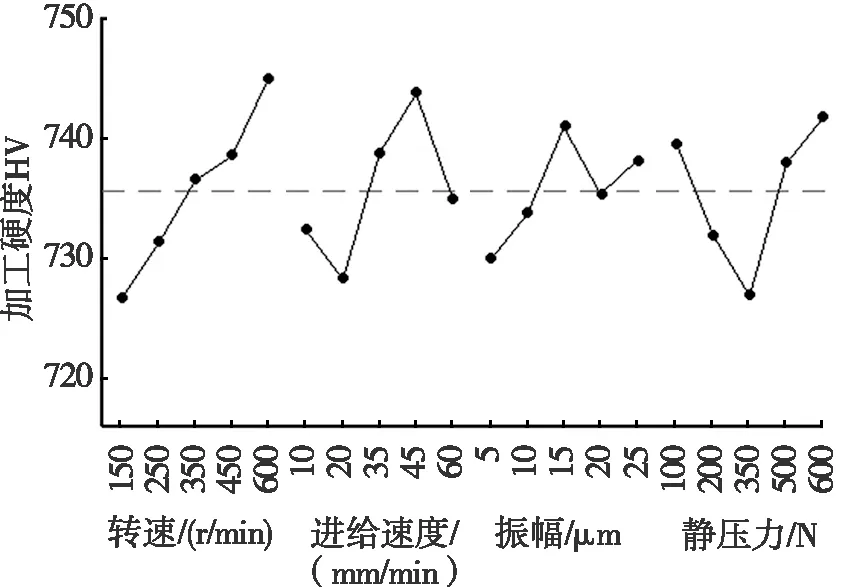
圖6 加工硬度主效應圖

3.3 優化結果分析

通過超聲滾擠壓軸承套圈表層性能的信噪比，賦予表層性能綜合熵權權重下的最優加工參數水平為n=350 r/min，f=60 mm/min，A=10 μm，F=200 N，如表6所示。由加工參數對表層性能的主效應圖可以得到要使表面粗糙度最小，應取加工參數水平n=150 r/min，f=20 mm/min，A=20 μm，F=350 N；要使殘余壓應力最大，應取加工參數水平n=600 r/min，f=60 mm/min，A=10 μm，F=100 N；要使加工硬度最大，應取加工參數水平為n=600 r/min，f=45 mm/min，A=15 μm，F=600 N。

表6 綜合表層性能信噪比

由上述優化結果設置7組試驗并代入二階響應預測模型進行對比驗證，如表7所示。

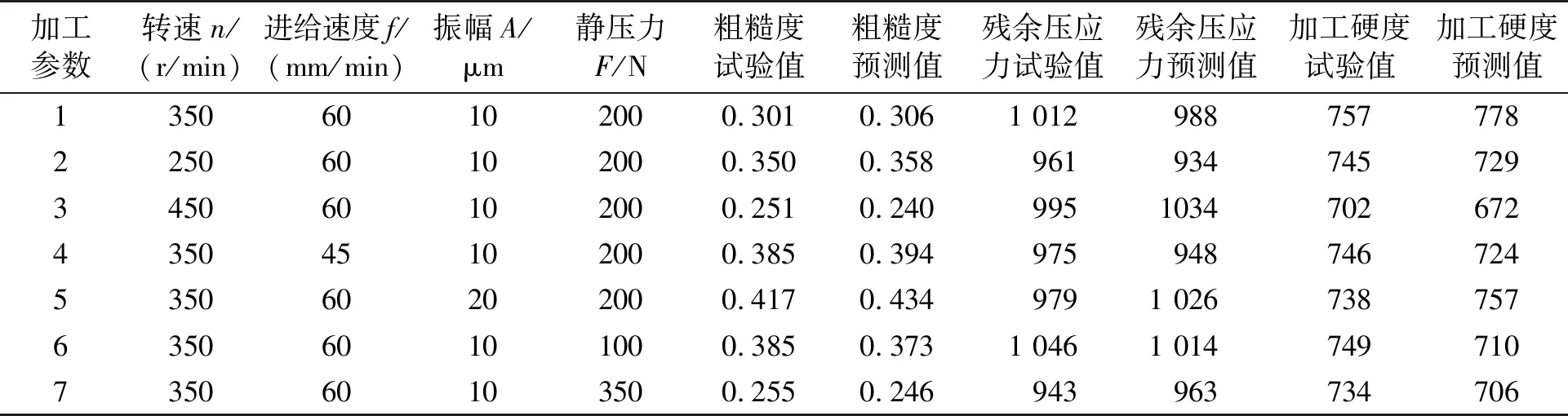
表7 驗證結果

由表7得出：7組試驗中表面粗糙度試驗值與預測值誤差分別為-1.6%、-2.3%、4.4%、-2.3%、-4.1%、3.1%、3.5%；殘余壓應力試驗值與預測值誤差分別為2.4%、2.8%、-4.3%、2.8%、-4.8%、3.0%、2.1%；加工硬度試驗值與預測值誤差分別為-2.8%、2.1%、4.3%、2.9%、-2.6%、5.2%、3.8%。試驗誤差均控制在6%以下，證明了預測模型的準確性。結合表7發現：第3組、第7組試驗表面粗糙度值比優化組合得到的值較優，但殘余壓應力值和加工硬度值沒有優化組合得到的值優；第2組、第4組的表層性能的試驗值均沒有優化組合得到的值優；第5組、第6組的殘余壓應力值比優化組合優，但表面粗糙度值、加工硬度值劣于優化組合的值。綜上，在進行多目標優化時，優化組合得到的值實現了表層性能的全局最優，進一步使軸承套圈表層性能得到改善。

4 結論

(1)通過信噪比基本特性計算超聲滾擠壓軸承套圈加工參數的變異系數，得到加工參數對軸承套圈表層性能的影響顯著性：靜壓力>進給速度>轉速>振幅。

(2)通過信噪比計算軸承套圈表層性能的信噪比，結合綜合熵權理論對表層性能的權重，得到超聲滾擠壓軸承套圈表層性能的最優加工參數組合：n=350 r/min，f=60 mm/min，A=10 μm，F=200 N，并由預測模型和對比試驗驗證了其精確性。

(3)通過對超聲滾擠壓軸承套圈的加工參數進行主效應分析，得到超聲滾擠壓的加工參數在各水平內對軸承套圈表層性能的影響規律各不相同，以及在各表層性能最佳時的最優加工參數組合：表面粗糙度最優時參數水平為n=150 r/min，f=20 mm/min，A=20 μm，F=350 N；殘余壓應力最優時參數水平為n=600 r/min，f=60 mm/min，A=10 μm，F=100 N；加工硬度最優時參數水平為n=600 r/min，f=45 mm/min，A=15 μm，F=600 N。