左旋尋常的極光千米波與輻射帶高能電子相互作用的參數化研究*

李文濤 張賽 賀佳貝 鄧舟坤 楊奇武 商雄軍 周慶華

1(長沙理工大學物理與電子科學學院 長沙 410114)

2(中國科學院空間天氣學國家重點實驗室 北京 100190)

3(騰訊云計算(長沙)有限責任公司 長沙 410221)

4(湖南省普通高校重點實驗室 近地空間電磁環境監測與建模實驗室 長沙 410114)

0 引言

極光千米波（Auroral Kilometric Radiation，AKR）是地球磁層等離子體中相速度大于光速的電磁波，頻率在30～800 kHz，功率可達107～109W[1-3]。目前，普遍認為極光千米波是來自磁尾的超熱電子（能量1～10 keV）在極區由于電子回旋注入不穩定性ECMI（Electron Cyclotron Maser Instability）激發的[4]。空間等離子體中的極光千米波存在三種模式，即右旋奇異（Right-hand Extraordinary,R-X）模、左旋尋常(L-O) 模和左旋奇異（Left-hand Extraordinary,L-X）模。極光千米波的產生機制預測地球磁層中的極光千米波主要以R-X 模為主，很多觀測數據也證實了這一點[4-8]。Summer等[9]研究了第一階共振驅動的極光千米波與輻射帶電子的相互作用，結果表明極光千米波能夠對高能電子產生明顯加速效應。隨后，Xiao等[10]構建了包含波磁場分量的極光千米波局地擴散系數表達式。在此基礎上，Xiao等[11,12]隨后使用假設的極光千米波磁場分量參數，計算了由15 階共振驅動的極光千米波彈跳平均擴散系數，結果表明極光千米波能在一天內對電子產生有效加速，甚至能將電子能量加速至約100 倍，而這些被加速的電子有可能嚴重威脅航空系統及空間天氣。

由于極光千米波的源區位于高度為1～3Re的高緯極光區[1,3,13]，因此早期對極光千米波的觀測主要集中在高緯區域。2015 年Kurth等[14]基于Van Allen 探測器的數據報道了輻射帶低緯區域的極光千米波，說明產生于極區的極光千米波能夠出現在輻射帶甚至赤道附近。Xiao等[15]利用3D 射線追蹤方法研究了不同地磁條件下極光千米波的傳播，證明在一定條件下極光千米波可以從高緯極區傳播至低緯區域甚至赤道區域。2019 年基于Van Allen 探測器數據的統計結果表明，輻射帶的極光千米波存在于L為3～6.5 和整個磁地方時的廣泛區域[16,17]。

由于缺乏高頻電磁波磁場分量的觀測數據和其他判斷電磁波極化的手段，之前對極光千米波的傳播機制及其與電子相互作用的研究主要是基于極光千米波為R-X 模的假設。雖然Hanasz等[18]2003 年在使用Interball-2 數據研究極光千米波發生率分布的工作中發現磁層高緯區域存在L-O 模，但是輻射帶的中低緯區域長期以來沒有關于L-O 模的報道，因此關于輻射帶中L-O 模與電子之間的相互作用尚未被系統性研究。2018 年Nakamura等[19]利用Arase 衛星觀測數據報道了極光千米波極化的研究事例，發現在輻射帶中不僅存在R-X 模，同時也存在L-O 模。基于此，本文通過改變L-O 模的峰值頻率(ωm)、傳播角(θ)分布和緯度(λ)分布，計算電子彈跳平均擴散系數，參數化研究L-O 模與外輻射帶高能電子的相互作用。

1 模型介紹

在忽略離子運動及無碰撞的冷等離子體時，高頻斜傳播的L-O 模的色散關系為[9,10,20]

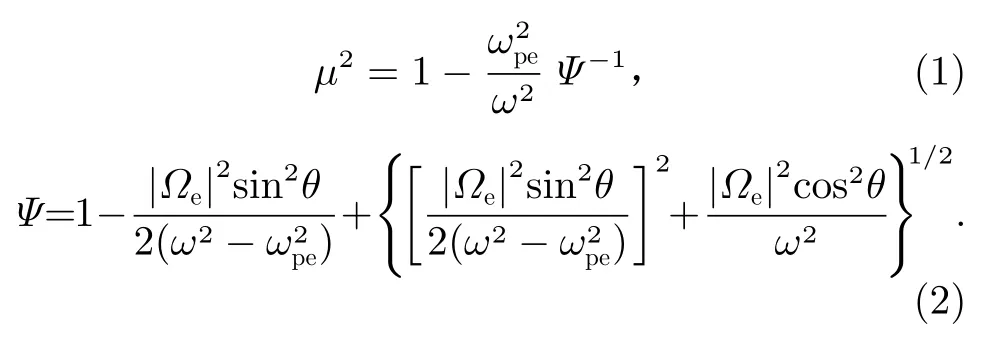
其中，μ為等離子體的折射率，ω為波的角頻率，ωpe為電子等離子體頻率，Ωe為電子回旋頻率，θ為波傳播角。根據波的色散關系得到L-O 模的下截止頻率為

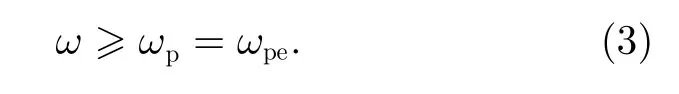
電磁波與電子之間的n階諧波回旋共振條件為

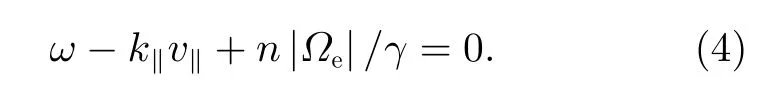
其中，k‖=kcosθ為波的平行波數；v‖=vcosα，v為電子速度，α為電 子投擲角；γ為洛倫茲因子。由于極光千米波為超光速波，由其定義可知相速度u=ω/k ＞c，回旋共振階數n只能取負值-1，-2，-3，···，∞。

在描述波粒相互作用的準線性擴散方程中，彈跳平均的投擲角擴散系數、動量擴散系數和交叉投擲角擴散系數＜Dαα＞，＜Dpp＞，＜Dαp＞=＜Dpα＞具體形式為[21,22]

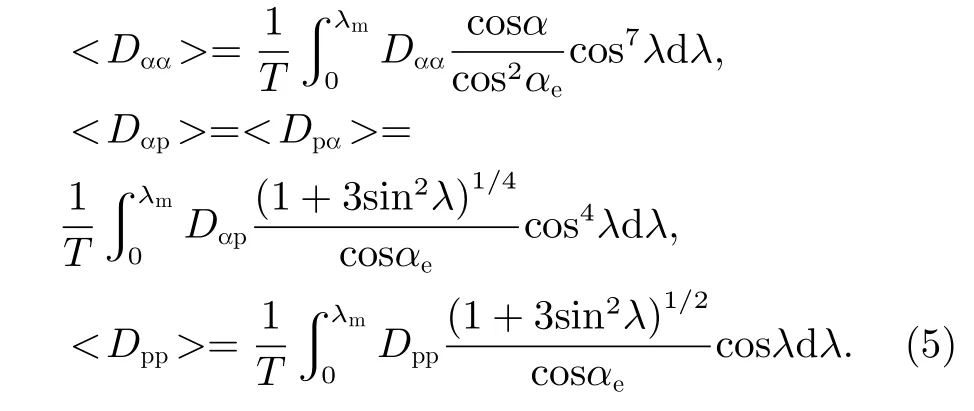
式中，歸一化的彈跳時間可以通過T(αe)≈1.30-0.56sinαe得 到，這里αe為 電子赤道投擲角；λm為L-O模存在的最大緯度，Dαα，Dpp，Dαp=Dpα分別為局地的投擲角擴散系數、動量擴散系數及交叉投擲角-動量擴散系數，其均具有與p2/t相同的量綱[22-24]。局地擴散系數矩陣D的每個元素均可以表示為一個在波的傳播角范圍內對X（X=tanθ）的積分和對所有共振階數n的求和，即

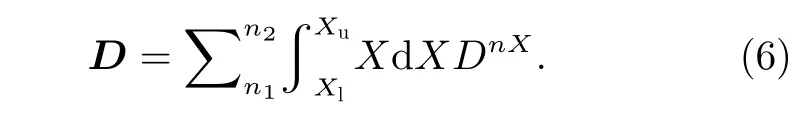
其中，Xl為 傳播角正切值的下限，Xu為傳播角正切值的上限，并滿足高斯分布。

根據以往研究[10]可以求得投擲角擴散系數

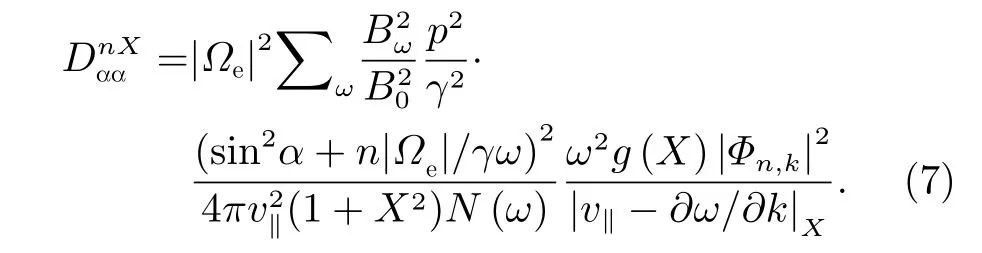
其中，B0為背景磁場強度，ω取所有共振頻率，|Φn,k|2與 波的色散關系相關，N(ω)則是一個使得每單位頻率的波能量等于的歸一化因子，后兩個量在之前的研究中已經得到[22,25]。而交叉及動量局地擴散系數與的關系如下：

2 數值結果與分析

此前對極光千米波的研究表明，在一定條件下極光千米波能夠從高緯極區傳播進入輻射帶的低緯區域，甚至到達低緯赤道附近。在這些區域，輻射帶中的高能電子會與極光千米波發生回旋共振，這可能引起高能電子的顯著加速，從而導致空間天氣災害的發生。Xiao等[11]曾針對R-X 模的極光千米波對輻射帶電子的動力學演化進行了系統的參數化研究。以此為參考，這里通過計算L-O 模在不同的峰值頻率(ωm)、傳播角(θ) 分布和波緯度(λ)分布情況下，輻射帶電子的彈跳平均擴散系數，對L-O 模與輻射帶電子的相互作用進行參數化研究。

分析中假設是在強磁暴（KP=5）期間的 L-O 模與高能電子發生階數n為-1～15 的回旋共振作用，其發生區域為L=4.5 的外輻射帶區域。在磁暴發生期間，等離子層頂會向地球壓縮，導致所選區域的等離子體密度變低（這里選取的等離子體密度參數ωpe2/Ωe2=2.0，電子數密度n0=ωpe2ε0me/e2=2.0Ωe2ε0me/e2，其中ε0為 介電常數，me為電子質量，e為電子電荷量值）[26]；極光千米波的波幅度在磁暴時可以達到0.1 nT 左右[27]，這里選取L-O 模的幅度Bt=0.1 nT。根據既有研究結果，極光千米波的傳播路徑十分傾斜[9,28]，且目前缺少輻射帶關于極光千米波傳播角的具體觀測數據。為使模擬結果更加準確，這里選取較大的 L-O 模傳播角范圍作為計算擴散系數的參數。采用的參數具體如下：Xl=tan5°，Xu=tan89°，Xm=tan60°，Xω=tan50°。選擇的頻率參數為ωl/(2π)=10 kHz，ωu/(2π)=500 kHz，δω/(2π)=100 kHz。同時假設L-O 模存在于沿著整個磁場線的所有緯度，具有恒定的波幅Bt=0.1 nT。

2.1 波的不同峰值頻率對輻射帶電子的影響

為研究峰值頻率ωm對L-O 模與輻射帶電子相互作用的影響，分別考慮ωm/(2π)=150 kHz，250 kHz和350 kHz三種情況。

從圖1 中可以明顯發現，當峰值頻率為150 kHz時，1 MeV 以下能量電子的有效擴散系數（＞ 10-9s-1）覆蓋了整個投擲角范圍，擴散系數隨著電子能量的增加而逐漸減小。隨著波的峰值頻率從150 kHz 增大到350 kHz，投擲角、動量以及交叉擴散系數覆蓋的投擲角區域逐漸減小。同時，從圖1 中可以得知，對于三種峰值頻率的L-O 模與電子相互作用，有效的動量擴散系數覆蓋的投擲角范圍均大于投擲角擴散系數覆蓋范圍。

圖1 不同峰值頻率的投擲角（上）、動量（中）及投擲角-動量交叉（下）彈跳平均擴散系數2D 結果Fig.1 2D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom)

圖2 表明，在小投擲角區域（＜ 30°），峰值頻率為150 kHz 的L-O 模對1 MeV 的電子，動量擴散系數比投擲角擴散系數約高10 倍；但是在大投擲角處（＞ 60°），動量擴散系數比投擲角擴散系數高約100 倍，這說明L-O 模對電子的主要作用是導致其動量擴散，因此L-O 模具有加速電子的可能。圖3 給出了1 MeV 能量電子的投擲角擴散系數與動量擴散系數的對比，研究表明，對于這三種不同峰值頻率的L-O 模，擴散系數均隨投擲角的增大而下降，特別是在峰值頻率為250 kHz 和350 kHz 時，隨著投擲角的增大，擴散系數的下降更為迅速。此外，對比分析三種頻率的擴散系數，可以發現彈跳平均擴散系數會隨著峰值頻率的增加而降低。這是因為在其他條件不變的情況下，L-O 模與電子共振時，共振頻率大多集中在較低頻率且不會隨峰值頻率變化，當峰值頻率增加時，這些共振頻率會越遠離峰值頻率，共振能量將減弱，使得擴散系數減小，這與R-X 模的情況較為相似[11]。

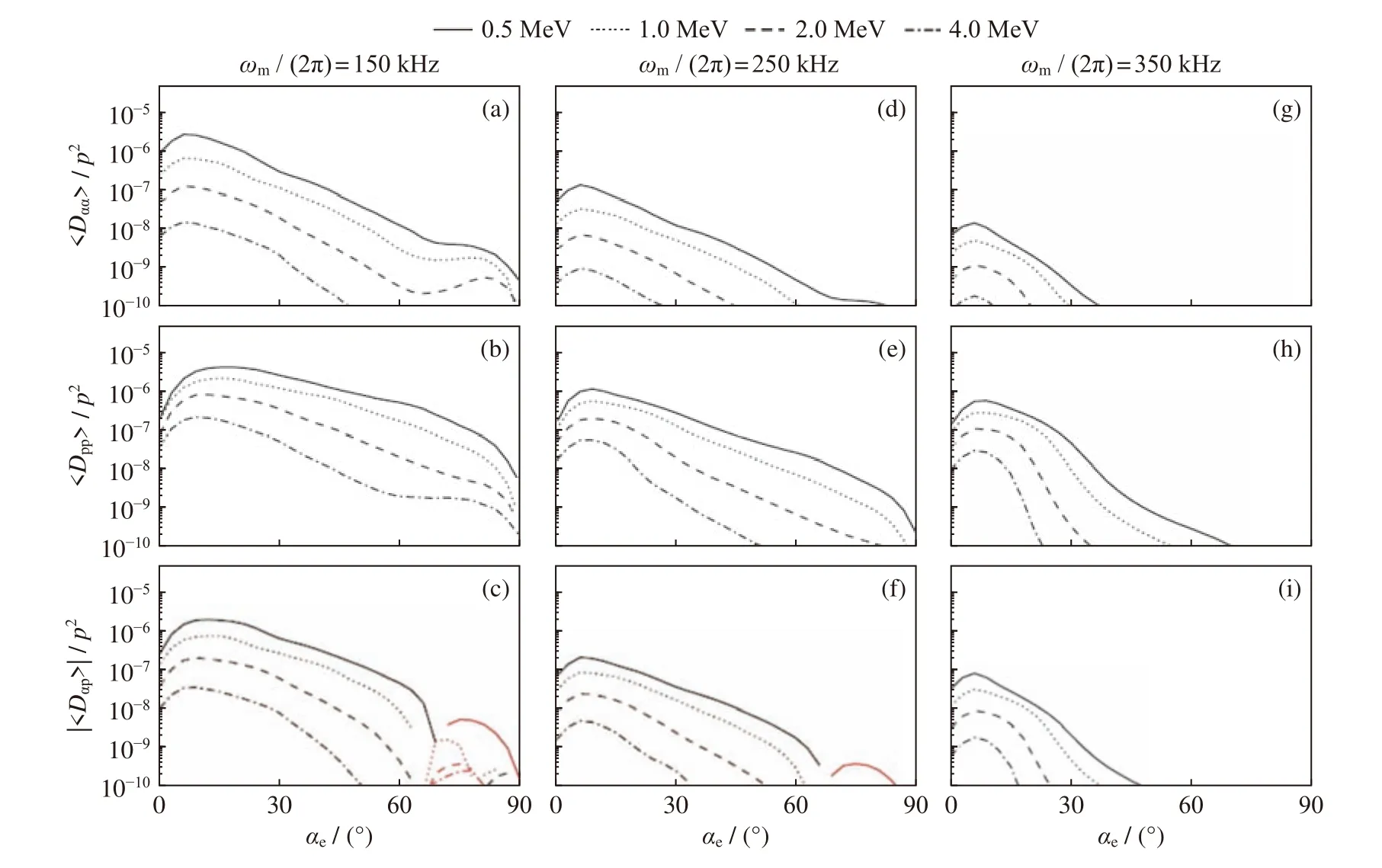
圖2 不同峰值頻率的投擲角（上）、動量（中）及投擲角-動量交叉（下）彈跳平均擴散系數1D 結果Fig.2 1D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom)

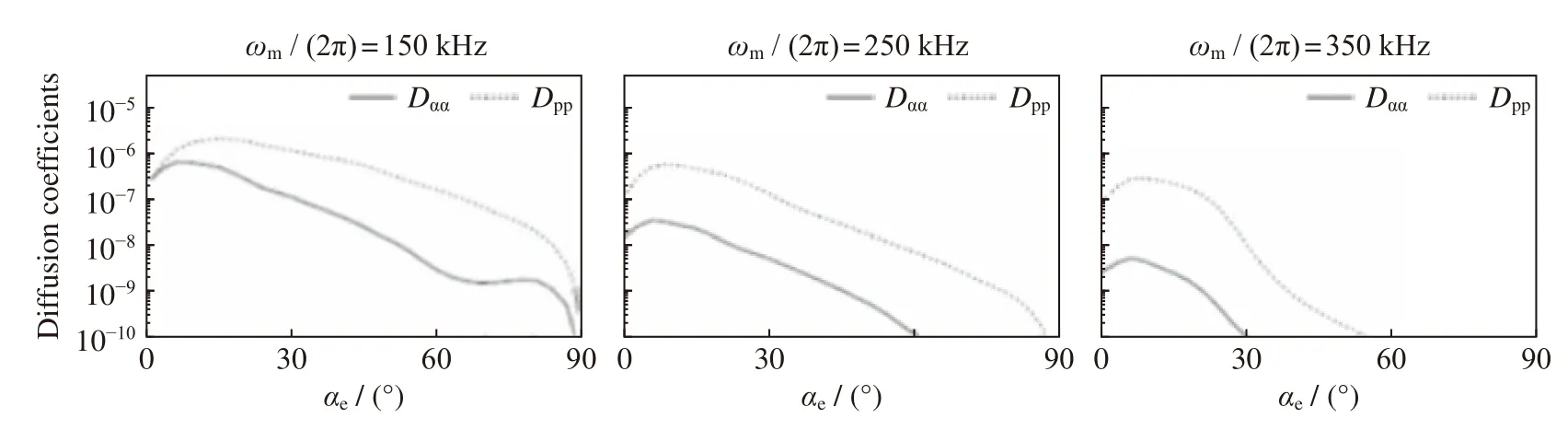
圖3 能量為1 MeV 的投擲角擴散系數（Dαα）與動量擴散系數（Dpp）的對比Fig.3 Comparison of the pitch angle diffusion coefficient (Dαα) and momentum diffusion coefficient (Dpp) with energy of 1 MeV

2.2 波的不同傳播角分布對輻射帶電子的影響

此前針對準線性散射率對亞光速合聲波傳播角分布情況的敏感性研究發現，散射率對高能量波的傳播角分布相對不敏感[29]。2007 年Xiao等[28]基于射線追蹤技術針對極光千米波傳播路徑的研究發現，極光千米波初始傳播角的不同會在一定程度上影響其傳播路徑。

為研究不同傳播角對L-O 模與輻射帶電子間相互作用的影響，選取了4 組不同L-O 模傳播角分布范圍進行計算與分析。這4 組范圍分別是：完整傳播角范圍5°＜θ＜89°，中等及大的傳播角范圍25°＜θ＜89°，大傳播角范圍45°＜θ＜89°，中等傳播角范圍45°＜θ＜65°。計算采用的波的傳播角參數均與2.1 節中一致。在4 種傳播角范圍的計算中采用的L-O 模峰值頻率均為ωm/(2π)=150 kHz。

圖4 給出的是在4 種不同L-O 模傳播角分布情況下的二維電子彈跳平均擴散系數。從情況1～3 可以明顯看出，在最小傳播角不同而最大傳播角相同的條件下，三種情況之間的擴散系數沒有明顯差異。圖4 中，情況4 采用的最小傳播角與情況3 是一致的，最大傳播角則與前三種情況不同，但是可以發現情況4 的擴散系數與前三種情況未發生較大變化，因此可從圖4 中得到在峰值傳播角及半寬帶不變的情況下，傳播角范圍對L-O 模與電子相互作用的擴散系數影響很小。

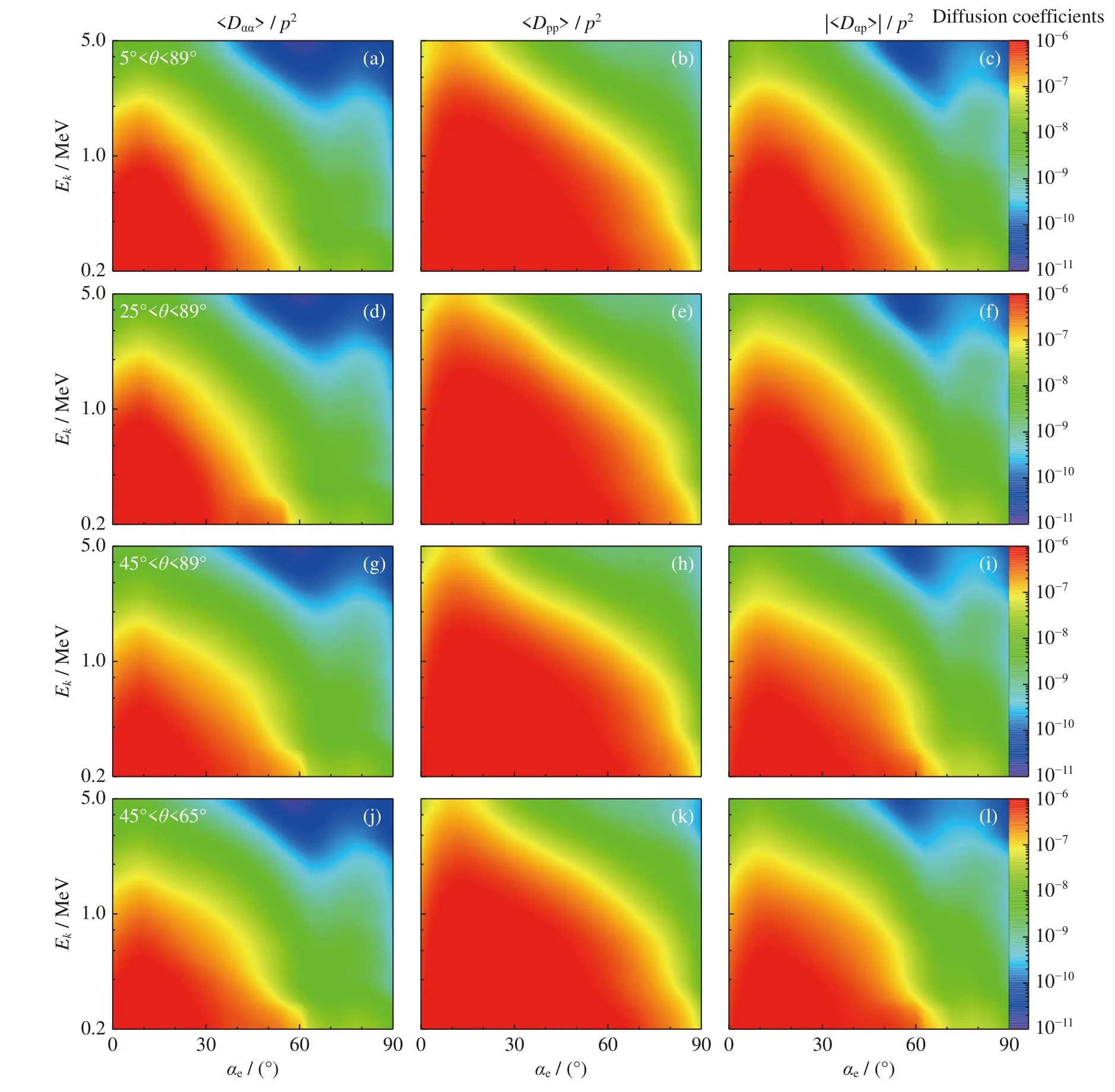
圖4 不同傳播角分布的投擲角（左）、動量（中）及投擲角-動量交叉（右）彈跳平均擴散系數2D 結果Fig.4 2D bounce-averaged diffusion coefficients of pitch angle (left),momentum (middle),and cross (right) for different wave normal angle distributions

圖5 是與圖4 對應的一維擴散系數，與圖4 類似，在最小傳播角不同而最大傳播角相同的條件下（情況a～c），三種情況的擴散系數沒有明顯差異。在最大傳播角變小后（情況j～l），擴散系數相比前三種情況同樣未發生明顯變化，同樣也能說明在峰值傳播角及半寬帶不變的情況下，L-O 模與電子相互作用的擴散系數對傳播角范圍的依賴較弱。

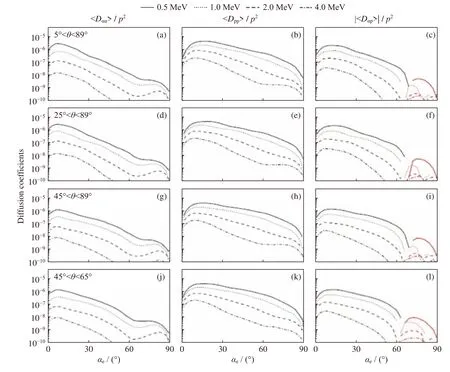
圖5 不同傳播角分布的投擲角（左）、動量（中）及投擲角-動量交叉（右）彈跳平均擴散系數1D 結果Fig.5 1D bounce-averaged diffusion coefficients of pitch angle (left),momentum (middle),and cross (right)for different wave normal angle distributions

2.3 波的不同緯度分布對輻射帶電子的影響

既有研究結果表明，波存在的緯度分布會影響其與粒子之間的相互作用[30,31]，R-X 模對電子的動力學影響會隨著緯度的不同而發生變化，高緯的R-X 模會導致電子投擲角散射，而在赤道附近或者低緯處，則會有效加速電子[32-34]。

為了探究不同緯度分布對L-O 模與輻射帶電子相互作用的影響，同樣選擇三個具有代表性的L-O 模緯度分布范圍計算擴散系數：所有緯度區域（λ＞0°），中高緯度區域（λ＞20°），高緯區域（λ＞40°）。在此計算中采用的L-O 模的峰值頻率同樣為ωm/(2π)=150 kHz。

圖6 給出的是在三種不同L-O 模緯度分布情況下，電子二維彈跳平均投擲角、動量及投擲角-動量交叉擴散系數。從圖6(a)～(c)可以清晰發現，在緯度分布為所有緯度區域時，有效擴散系數覆蓋了整個投擲角范圍。然而隨著緯度分布變為中高緯區域后，擴散系數會移動到較小的投擲角區域（＜60°）如圖6(d)～(f)所示。到了高緯區域時，擴散系數只存在于30°以內的投擲角區域，如圖6(g)～(i)所示。同時，隨著波存在緯度范圍的減小，擴散系數會有一個數量級左右的減小。

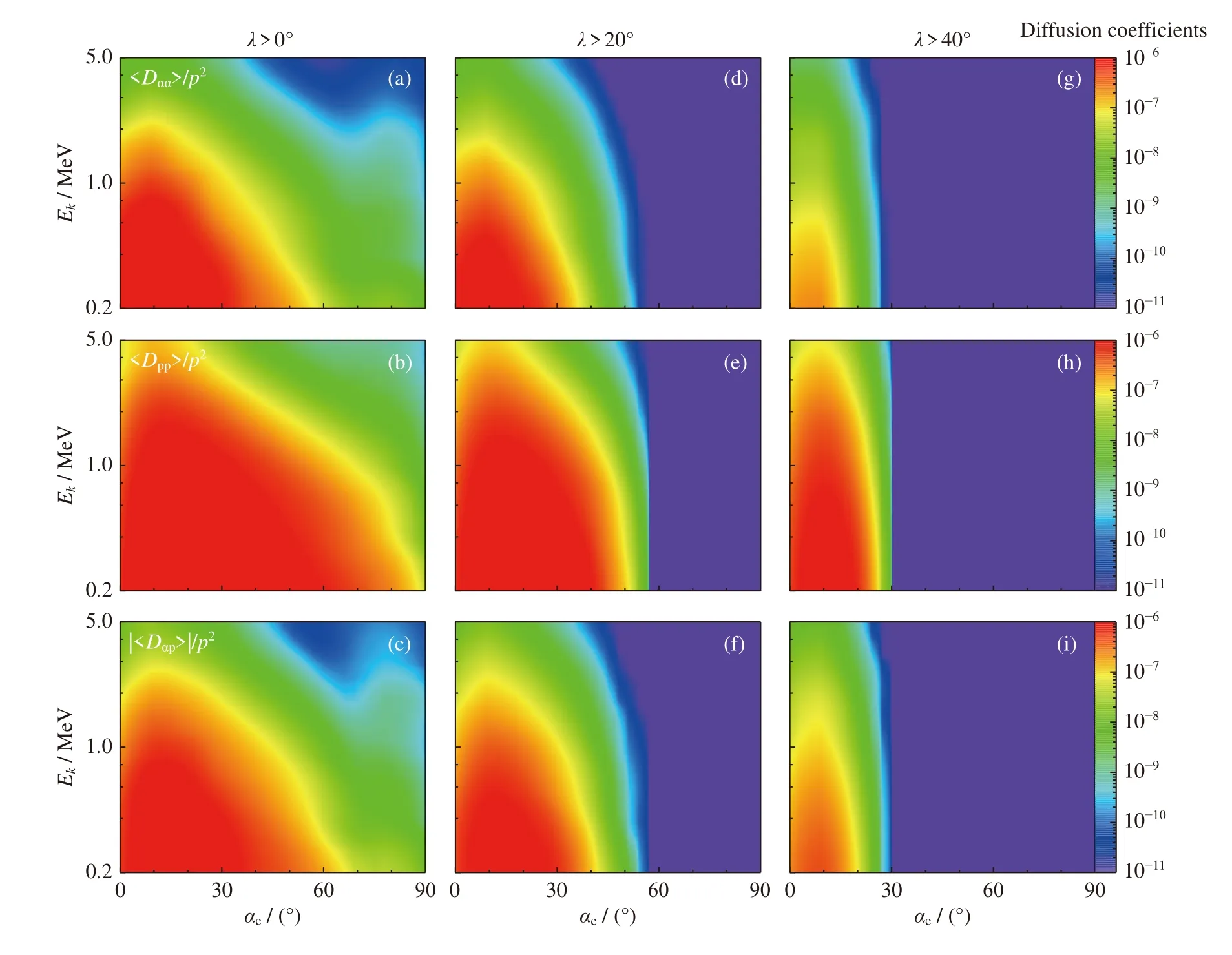
圖6 不同緯度分布的投擲角（上）、動量（中）及投擲角-動量交叉（下）彈跳平均擴散系數2D 結果Fig.6 2D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom) for different wave latitudinal distributions

圖7 是與圖6 對應的不同能量電子的一維擴散系數。如圖7(a)～(c)所示，當緯度分布為整個緯度區域時，在整個投擲角區域中，擴散系數變化較為平緩。但是在中高緯度區域，擴散系數在投擲角為50°附近會急劇下降，如圖7(d)～(f)所示。而在高緯區域，在投擲角為25°時擴散系數急劇下降，如圖7(g)～(i)所示。這說明緯度分布對L-O 模與電子之間的相互作用有著較大影響，L-O 模存在的緯度變化會導致電子動力學過程發生劇烈變化。

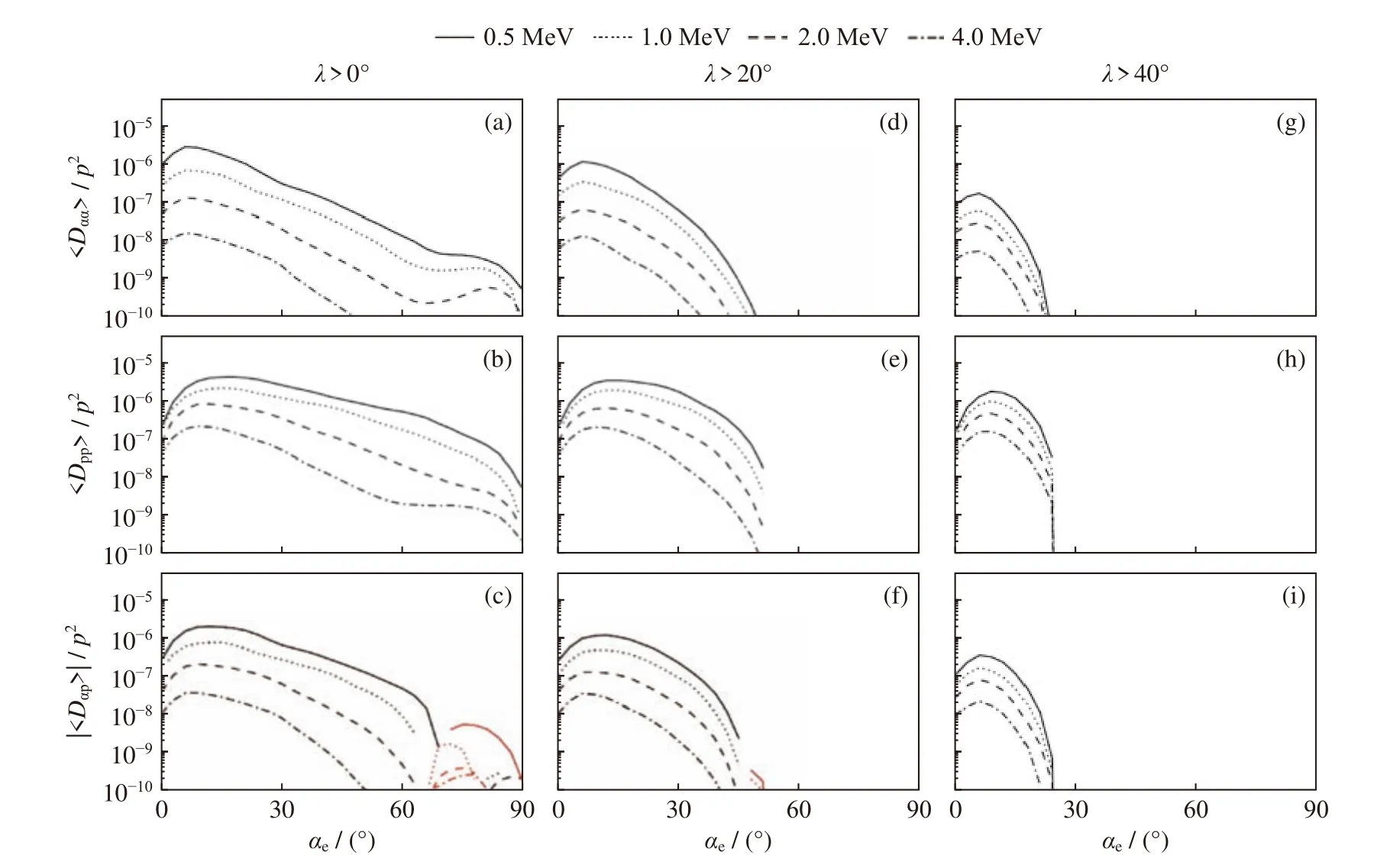
圖7 不同緯度分布的投擲角（上）、動量（中）及投擲角-動量交叉（下）彈跳平均擴散系數1D 結果Fig.7 1D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom) for different wave latitudinal distributions

3 結論

通過使用L-O 模3 組不同的峰值頻率參數、4 組不同的傳播角分布參數以及3 組不同的緯度分布參數，分別計算了電子彈跳平均的投擲角、動量及投擲角-動量擴散系數，探討了不同參數的L-O 模對輻射帶中高能電子的影響。得到結論如下。

（1）隨著L-O 模峰值頻率的增加，有效擴散系數覆蓋的投擲角范圍會逐漸減小，并且擴散系數也會逐漸減小。這可能是由于對電子彈跳平均擴散系數的影響主要來自波高斯分布的峰值頻率附近的根，而共振頻率大多集中在較低的波頻率附近。此外，動量擴散系數均大于投擲角擴散系數與交叉擴散系數，最大高出約100 倍，這說明L-O 模對電子的主要影響是導致其動量擴散，也證明L-O 模可能會對電子進行有效加速。

（2）在L-O 模的峰值傳播角及半寬帶不變，最大傳播角相同時，其與電子相互作用的擴散系數之間沒有明顯差異。在最大傳播角相同而最小傳播角不同時，擴散系數同樣沒有發生較大變化，說明L-O 模與電子相互作用的擴散系數與傳播角范圍之間沒有很密切的聯系。

（3）當緯度分布為整個緯度區域時，在所有投擲角范圍內，擴散系數的變化較為平緩。但是在緯度分布為中高緯區域時，擴散系數在投擲角50°附近會急劇下降。而在高緯區域，在投擲角為25°時擴散系數急劇下降。這說明緯度同樣會對L-O 模與電子之間的相互作用造成較大影響，L-O 模的緯度分布變化會對其與電子的相互作用過程發生顯著影響。

需要指出的是，Denton等[35]2002 年的研究工作發現，電子密度沿磁力線會隨緯度的升高而增加，在L=4.5 的磁力線上，L-O 模分布的維度范圍內電子密度變化不大（例如緯度50°處的電子密度是赤道處的1.76 倍）。在采用上述計算參數的情況下，場向密度變化對擴散系數的影響較小。為突出L-O 模的頻率、傳播角和分布緯度等特性在與電子相互作用中的影響這一重點，同時也為了減少計算量，這里沒有討論場向密度變化對擴散系數的影響，這方面研究將在今后工作中開展。同時，計算采用了假設的波譜參數，進一步的工作將基于衛星對L-O 模波的觀測數據，研究其與輻射帶電子的相互作用。