鋼管混凝土拱橋復雜節點局部力學性能分析
趙菊梅ZHAO Ju-mei
(云南工程建設總承包股份有限公司,昆明 650500)
0 引言
鋼管混凝土作為一種鋼結構和混凝土的組合材料,應用在拱橋結構中,能夠較大程度上減小拱橋的自重,提高其承載能力,增大拱橋整體跨徑長度[1],且在施工過程中的優越性以及較大程度的節約造價,使其在我國的公路建設中得到大量的發展和應用[2]。
鋼管混凝土是指在鋼管內灌注混凝土而形成的組合結構共同受力,鋼管的抗彎和彈塑性能力都較為優秀,而混凝土的抗壓能力較強,鋼管混凝土組合結構是將二者的優點結合起來,共同受力,其性能遠優于二者的簡單疊加。但同時,由于鋼管和混凝土的共同作用,使得鋼管混凝土的節點處于較為復雜的受力狀態下,尤其是在拱肋拱腳處的受力行為比較突出。本文以某鋼管混凝土拱橋為例,截取其拱肋拱腳位置處的幾何形狀進行有限元分析,結果表明,最大主拉應力出現在拱肋、拱腳和系梁交接處,最大主壓應力出現在拱肋與拱座連接處,在設計時應著重考慮該情況[3]。本文希望通過此文以了解此類型結構的受力和承載能力的特點,以期對類似工程提供參考。
1 拱肋拱腳幾何計算模型
主橋為計算跨徑L=115m的下承式鋼管混凝土系桿拱橋,拱肋采用啞鈴型鋼管混凝土結構,吊桿采用鋼絞線整束擠壓成品索,系梁、端橫梁及中橫梁采用預應力混凝土結構,風撐采用空鋼管結構,汽車荷載等級為公路—Ⅰ級,鋼材采用Q345D鋼。采用有限元軟件建立全橋模型后,提取其拱腳拱肋位置處的內力,建立有限元模型。
根據設計圖紙進行建模,有限元模型包括:拱腳伸出2.0m長的啞鈴型拱肋,拱腳實體部分,一半長度5.95m的端橫梁,拱座系梁取距離支座中心線6m區段。通過全橋桿系模型計算,按拱腳最不利荷載組合得到拱肋截面內力,如圖1所示,分別在拱肋和縱梁選取斷面加載,拱腳底施加支反力,端橫梁固結約束[4]。
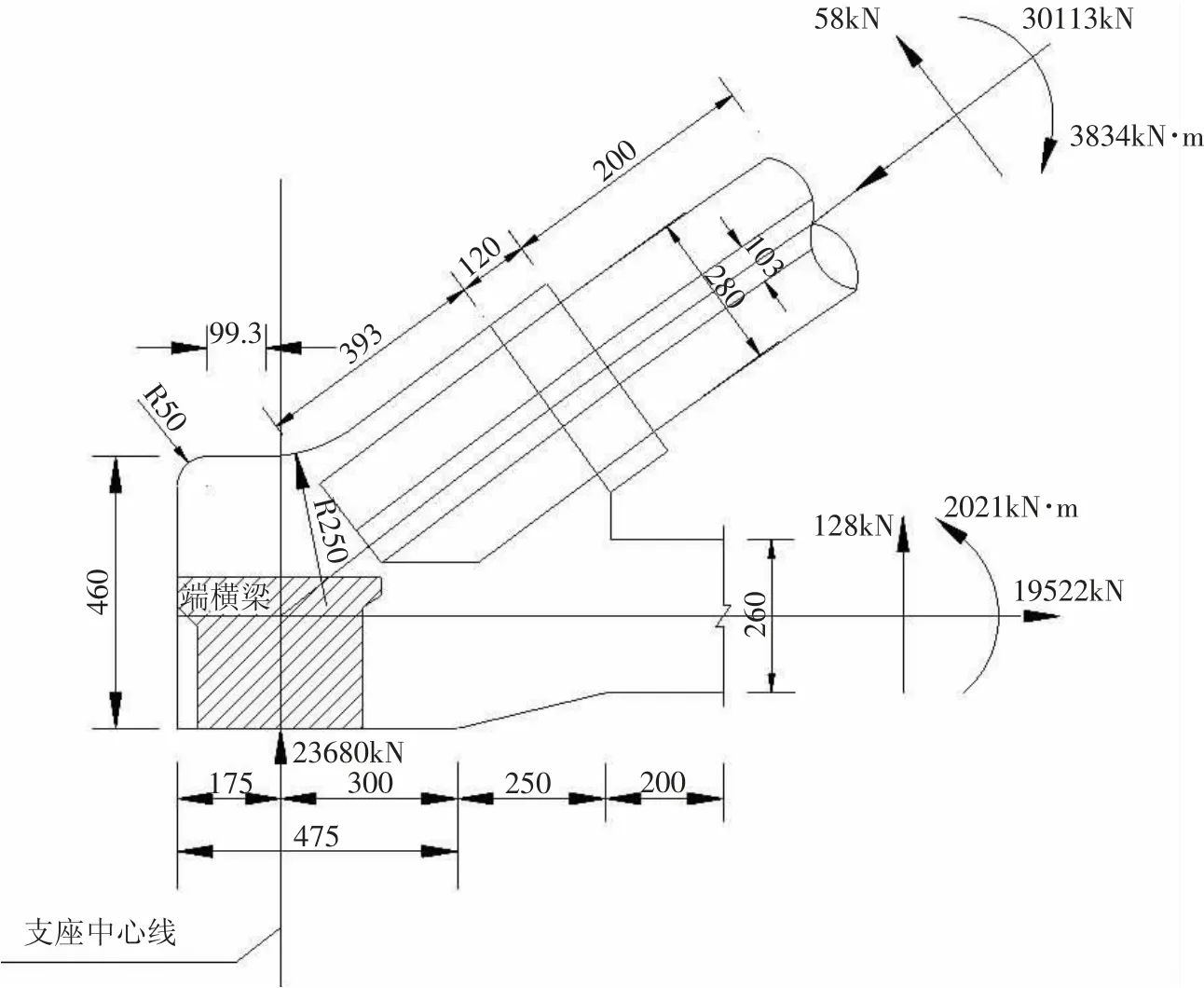
圖1 幾何尺寸及計算荷載
其中,在拱腳底施加23680kN的支反力,拱肋施加30113kN的軸力,58kN的剪力,3834kN·m的彎矩,在縱梁截斷界面處施加19522kN的軸力,128kN的剪力,2021kN·m的彎矩。
2 有限元模型
鋼管混凝土拱橋拱肋拱腳位置處的節點在拱橋整體結構受力范圍內是一個關鍵部位,鋼管混凝土的結合結構穿過拱座的混凝土,在其接觸位置的處理都是極為關鍵的,其次在成橋后,該處存在著拱肋、縱梁等諸多構件,在較大的負彎矩作用下,該處的受力情況是較為關鍵的[5]。因此根據結構具體尺寸,采用大型通用有限元程序建立計算模型,為避免拱肋邊界條件對研究區域的影響,主拱肋截取長度均為直徑的2倍以上,如圖2所示。
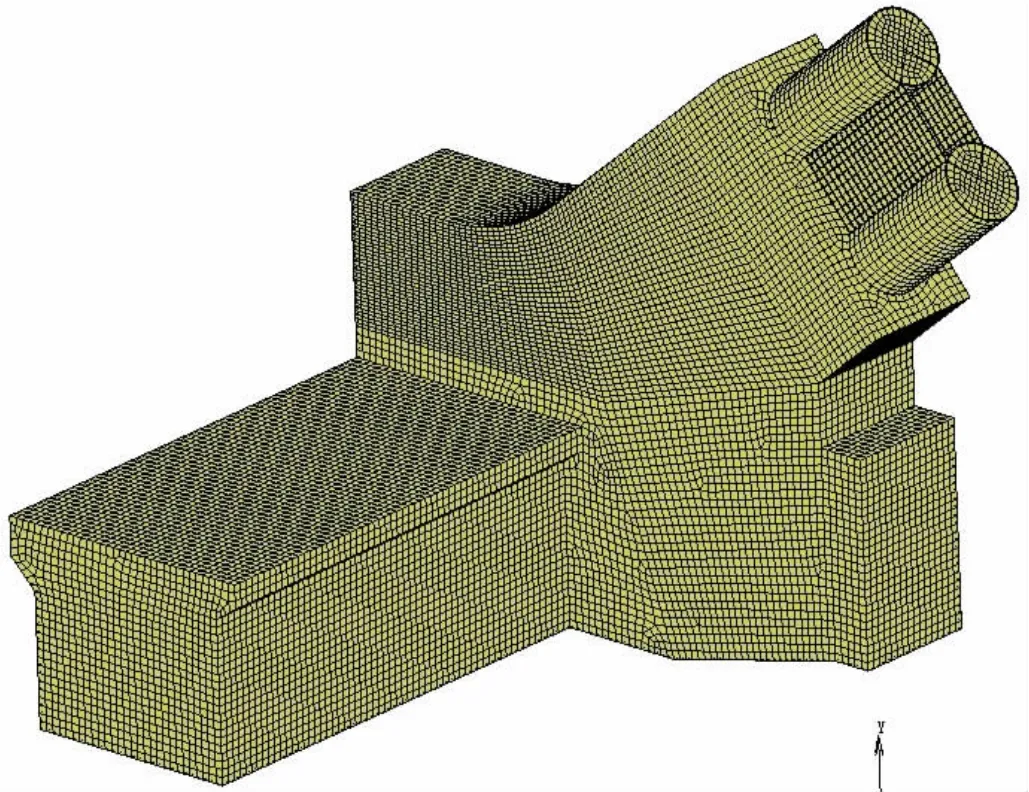
圖2 有限元計算模型
在系桿預應力錨固處、端橫梁預應力錨固處,按照實際預應力作用于錨墊板施加面荷載,在拱肋、縱梁加載面質心位置建立節點,與加載面上其他各點形成剛臂單元,最后在加載面上施加軸力、剪力、彎矩等節點荷載。同時在拱座底部施加固反力Y向反力,端橫梁端部施加固結約束[6]。
3 結構分析
3.1 應力分析
3.1.1 拱座位置處應力分析
首先進行拱腳位置處拱座的受力進行分析,模型中的最大主壓應力如圖3。
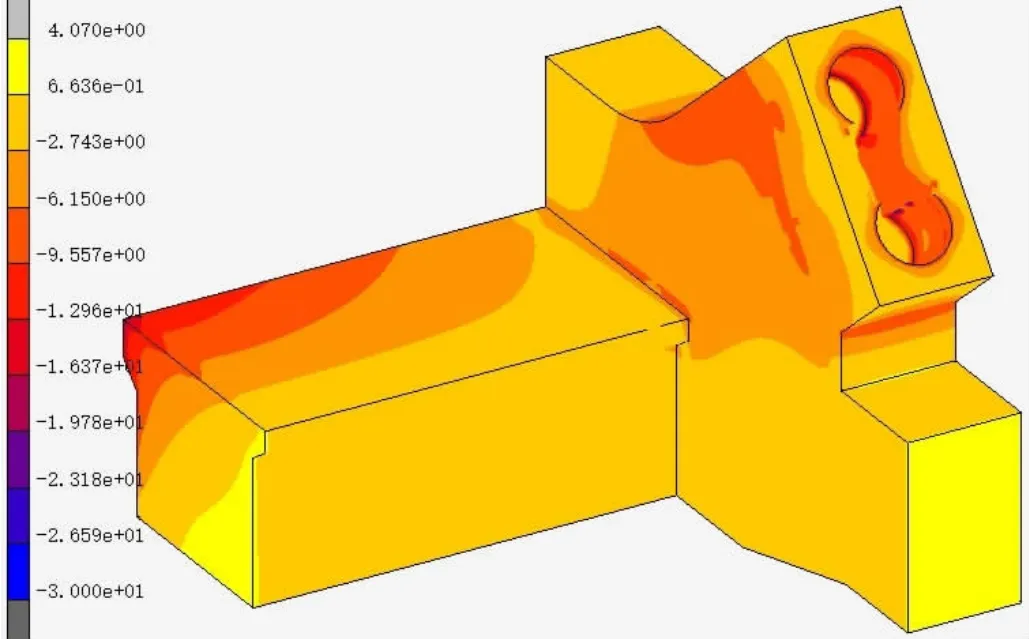
圖3 拱座混凝土最大主壓應力云圖
從圖中可以看出,在啞鈴型拱肋嵌入拱座位置處的極個別點的最大主壓應力能達到30MPa,這是因為在該處屬于拱肋與拱座的連接,在拱肋上的荷載傳遞到連接處,造成該處的局部應力會增大,其次就是在拱座與拱肋連接的轉彎處,最大主壓應力有13MPa,這是因為拱肋上傳遞下來的荷載整體是由該部承擔了大部分荷載,造成該處的應力增大,但均滿足混凝土抗壓強度的要求;最大主拉應力出現在拱肋、拱腳和系梁交接處,這是由于該處的受力是較為復雜的,有支座的支反力、橫梁傳遞過來的軸力、拱肋傳遞來的彎矩和軸力以及縱梁對其的傳遞效果,其最大主拉應力為1.51MPa,小于混凝土抗拉應力2.65MPa,滿足要求。設計人員在對此處進行設計時,應對橫梁、縱梁和拱肋連接位置處的應力進行適當的優化。
3.1.2 鋼管內混凝土應力分析
其次進行鋼管內混凝土的受力進行分析,模型中的最大主壓應力如圖4所示。
從圖4可以看出,鋼管內混凝土的主壓應力大體上是從里到外均勻層進的,這是因為混凝土的泊松比大于鋼管的泊松比,在軸心壓力作用下,混凝土的形變大于鋼管的形變,鋼管對混凝土形成了一個套箍作用,其最大主壓應力出現在拱肋與拱座連接處,為24.31MPa,其余部分混凝土抗壓應力小于32.4MPa,均小于C50混凝土的抗壓強度,滿足承載要求;鋼管內混凝土的主拉應力除端橫梁、拱腳和系梁交接處出現少量應力集中外,其余均小于混凝土抗拉應力2.65MPa,滿足承載要求。
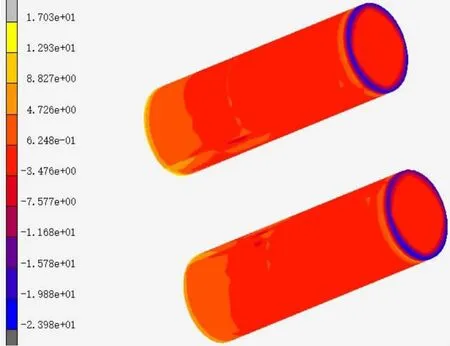
圖4 鋼管內混凝土最大主壓應力云圖
3.1.3 鋼管應力分析
隨后進行鋼管的應力分析,將其Mises應力云圖提取如圖5。
從圖5可以可以看出最大等效應力出現在拱肋端管中部,即除鋼管嵌入拱座混凝土內部的根部,這是因為嵌入拱座混凝土內部的鋼管與內外混凝土已形成整體,其受力反作用于此處,加上上部拱肋傳遞過來的荷載,因此此處的應力最大,達到了110.5MPa,但小于鋼管屈服應力345MPa;此外拱肋位置處的鋼管內外側的應力大小不同,這是鋼管內側起著約束內部混凝土的作用,其反作用下的應力要比外側大,且鋼管的壁厚對拱腳處應力的產生會有著較大的影響,因此設計時,在可以保證拱肋強度和穩定性的基礎上,合理優化鋼管的壁厚,可以達到防治拱腳應力集中的現象。
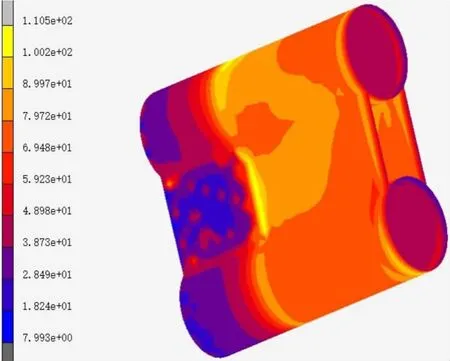
圖5 鋼管Mises應力云圖
3.2 剛度分析
最后對其在受力情況下整體的變形進行分析,將其變形結果圖形提取如圖6。
從圖6可以看出,最大軸力工況下,整個拱座沿橫橋向向橋面內變形,最大變形出現在系梁外側邊緣,為4.784mm,最小變形在端橫梁外側邊緣,為0.45mm。可以看出,該處結構的整體剛度比較大,固結區域的整體變形較小。能夠滿足規范要求。
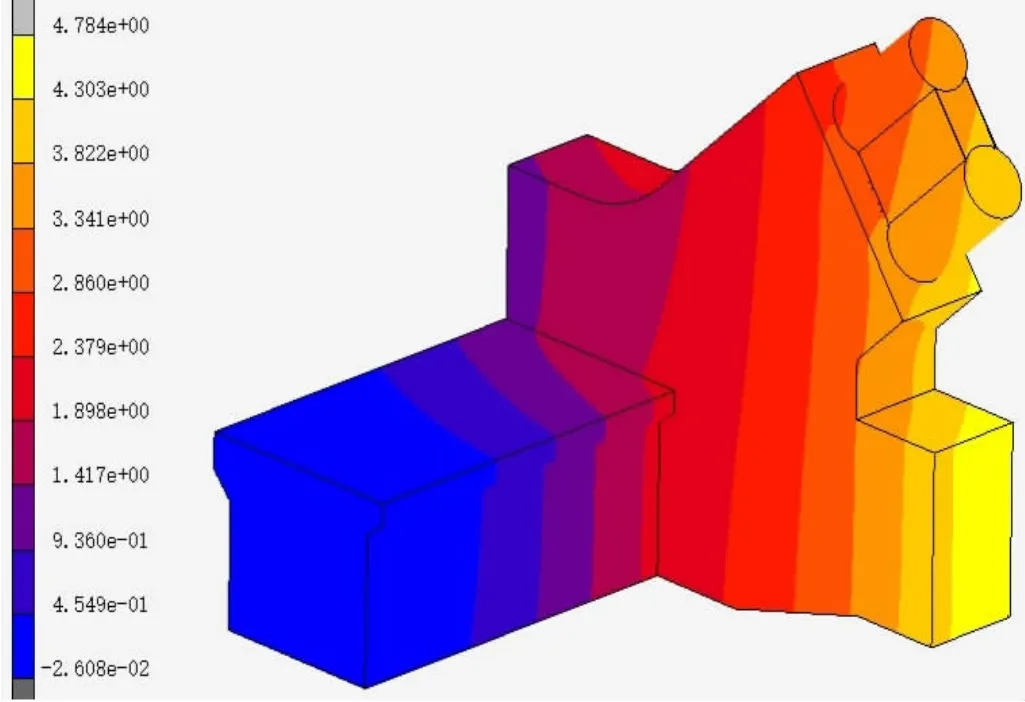
圖6 整體變形圖(單位:mm)
4 結論
本文以某鋼管混凝土拱橋為例,截取其拱肋拱腳位置處的幾何形狀進行有限元分析,對其整體結構變形、拱腳混凝土受力情況、鋼管內混凝土受力情況以及鋼管的整理受力情況進行分析,分析結果如下:
①結構變形:拱腳的結構剛度比較大,在拱腳最大軸力工況下,整個拱座沿橫橋向向橋面內變形,最大變形出現在系梁靠近橋面邊緣,為4.784mm。
②結構應力:除極個別點外,最大主壓應力為30MPa,滿足要求;最大主拉應力出現在拱肋、拱腳和系梁交接處,為1.51MPa,小于混凝土抗拉應力2.65MPa,滿足要求。最大主壓應力出現在拱肋與拱座連接處,為24.31MPa;除端橫梁、拱腳和系梁交接處出現少量應力集中外,主拉應力大于混凝土抗拉應力2.65MPa,滿足要求。最大等效應力出現在拱肋端管中部,為110.5MPa,小于鋼管屈服應力345MPa,滿足要求。
因此,設計人員在進行設計時,應著重對橫梁、縱梁和拱肋連接位置處的應力以及鋼管的壁厚進行考慮。本文可為相關工程提供參考。

