在線環(huán)境下客貨滾裝船多目標動態(tài)配載決策

張 煜 熊得鵬 馬少康 賀利軍 李 斌

(武漢理工大學交通與物流工程學院1) 武漢 430063) (福建工程學院交通運輸學院2) 福州 350118) (中交集團智慧研究院3) 武漢 430000) (武漢理工大學韶關研究院4) 韶關 512100)

0 引 言

客貨滾裝(以下簡稱“客滾”)運輸是一種旅客和渡海車輛相混合的運輸模式，客滾船配載作為客滾碼頭生產作業(yè)的核心環(huán)節(jié)，其配載效率和決策水平直接關系港口運作效率及其收益.與一般滾裝船配載相比，客滾船配載對象涉及小車、貨車和客車，且配載具有二維裝箱[1]、兩階段、實時動態(tài)等特點.

已有研究聚焦一般滾裝船配載問題(以規(guī)格尺寸相近的商品車為主)，將船舶配載視為背包問題[2]或者二維裝箱問題[3]，未具體考慮車輛在船艙中的擺放位置，不適用于客滾船配載場景.Zhang等[4]假設配載時所有渡海車輛信息已知，針對問題存在的兩階段、二維裝箱等特點，以船艙面積利用率最大為目標，設計了偏隨機密鑰混合算法.但在實際港口運作過程中，渡海車輛到港與船舶配載同步進行，配載時車輛信息是逐步獲取且無法完全已知.因此，客滾船配載還具有實時動態(tài)特點，需要引入在線決策，可借鑒在線車間調度[5]、在線裝箱[6-7]等方面的研究成果.

文中基于客滾船配載的現(xiàn)實需求，考慮問題的實時動態(tài)特點，將整個配載過程劃分為多個決策階段，構建基于車輛滾動窗口的客滾船多目標在線配載決策模型，設計了融合灰熵并行分析和混合遺傳算法的多階段動態(tài)決策框架及其算法，通過多組對比實驗來驗證模型和算法的有效性.

1 問題描述

客滾船配載的兩階段是指配載前中期車輛需全部裝入船艙，記為主體配載階段(main stowage planning phase, MSPP)；配載后期挑選部分車輛裝船，記為補充配載階段(supplemental stowage planning phase, SSPP)，此階段允許小車旋轉放置.二維裝箱是指配載作業(yè)的維度、規(guī)則和目標與二維裝箱問題的裝箱維度、裝箱規(guī)則和裝箱目標一致.此外，配載時還需考慮船舶穩(wěn)性和車輛間的安全距離，以保證船舶安全航行.以瓊州海峽為例，客滾船配載過程中，港方動態(tài)獲取抵港車輛信息，實時配載客滾船，直至船艙裝滿或達到額定載重量的90%，停止配載.以往研究中，針對此類在線決策問題，多采用滾動策略進行求解[8].為此，本文設計了一種滾動推進策略，將一個完整的配載過程劃分為多個耦合的決策階段，根據(jù)每個階段的車輛信息生成一個滾動窗口，進行局部最優(yōu)求解，并將上一階段的船艙最終狀態(tài)作為下一階段的初始狀態(tài)，利用車輛到港數(shù)量驅動窗口信息更新和決策階段前進，見圖1.

圖1 客貨滾裝船在線動態(tài)配載決策

為實現(xiàn)滾動推進策略的數(shù)學化描述，定義以下概念：車輛序號集合I為按到港順序依次編號，I={i|i=1,2,…,|I|}；I1為MSPP車輛序號集合，I1={i|i=1,2,…,|I1|}；I2為SSPP車輛序號集合，I2=I-I1；Sd(t)為第t階段滾動窗口中的車輛集合；H為滾動窗口最大長度即Sd(t)中的車輛數(shù)量.配載過程可描述為：初始，渡海車輛依次到港進入滾動窗口，當車輛數(shù)量達到H時，開始配載；在MSPP的第一個窗口決策階段，從Sd(1)中挑選車輛登船配載；后續(xù)車輛補充進入滾動窗口形成Sd(2)，通過不斷配載并更新Sd(t)，船艙狀態(tài)不斷向前推進(記為S-1階段).為符合配載兩階段性，MSPP臨近進入SSPP階段前，增設過渡階段，將MSPP剩余車輛全部裝船(記為S-2階段)；進入SSPP，先按照S-1階段配載作業(yè)，直至船艙裝滿或達到載重量要求時停止配載(記為S-3階段).此外，船艙是否裝滿取決于S-3階段配載完成后是否有車輛能夠繼續(xù)裝入.因此，為高效利用船艙面積，增設延遲驗收階段，在S-3階段配載完成后，等待Q輛車，判斷是否有車輛能夠裝入船艙(記為 S-4階段).

在線動態(tài)配載問題在各窗口決策階段，整體配載尚未完成，無法以船艙面積利用率最大為目標，但各階段均追求車輛擺放高度低且形成的配載面平滑；同時，由于貨車收費遠高于小車和客車，以航次收益為目標會導致優(yōu)先選擇貨車，不合港口服務宗旨.因此，本文以各決策階段的客滾船配載面高度最低和平滑度最高為目標，采用多目標優(yōu)化策略使各階段配載車輛盡量緊湊且配載面盡量平滑，其落腳點仍在于船艙面積利用率的最大化.

2 客滾船多目標在線動態(tài)配載決策模型

2.1 基本假設

1) 以船舶可配載區(qū)域的左下角建立xoy坐標系，見圖2.

2) 假設船艙和車輛為質量均勻的矩形.

3) 將船艙劃分成若干網(wǎng)格，進行離散化描述，單元格采用二元組(j,k)進行標識，j、k分別表示第j列和第k行.

4) 假設待配載車輛數(shù)大于船舶最大容量，車輛信息未知.

圖2 船艙狀態(tài)離散化描述

2.2 符號及變量說明

符號與集合：DIt,DIst,DIbt為當前決策窗口t中的車輛序號集合、小車序號集合、大車(客車和貨車)序號集合；i為待配載車輛序號，i∈DIt；j,k為船艙單元格的橫、縱坐標；

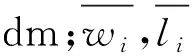
其他參數(shù)：mi為車輛i的質量，t；R為一個大數(shù)；G為船舶的額定載重量，t；Gt為在t階段，船舶的載重量，t；Ttx為在t階段，船舶的橫傾力矩，kN·m；Tty為在t階段，船舶的縱傾力矩，kN·m；Tx為船艙在x軸方向的最大橫傾力矩，kN·m；Ty為船艙在y軸方向的最大縱傾力矩，kN·m；N1為每次配載的車輛數(shù)；C1為過渡階段剩余車輛數(shù).

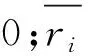
2.3 模型建立

若將配載面上單元格看成質點，則整個配載面由大量質點組成，以其下方單元格坐標作為該質點的位置標識，記為配載面質點，坐標表示為

(1)

(2)

則相鄰配載面兩質點間的曼哈頓二范式距離為

(3)

相鄰配載面質點在y軸方向上的浮動程度越大，則平滑程度越低.因此利用式(3)計算相鄰配載面質點的曼哈頓距離，并通過式(4)求和得到總距離來表征整個配載面的平滑程度δ.δ值越小，配載面越平滑.

(4)

由于S-1、 S-3階段的配載方式相同，針對S-1、 S-3階段的第t個滾動窗口，構建的基于車輛滾動窗口的客滾船在線配載決策模型，記為SPMS-1(t)或SPMS-3(t)，具體如下：

目標函數(shù)：

(5)

(6)

約束條件：

xijk≤ri+(1-si),?i∈

DI(s)t,j,k∈(M-Mi)

(7)

xijk≤(1-ri)+(1-si),

(8)

xijk≤(1-si)，?i∈DI(b)t,j,k∈(M-Mi)

(9)

(10)

(11)

(12)

xijk≤yij′k′+(1-ri),?i∈DI(s)t,j,

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(rili+(1-ri)wi-1-W)/2)+T(t-1)x≤Tx

(23)

(1-ri)li-1-L)/2)+T(t-1)y≤Ty

(24)

xijk,yijk∈{0,1},?i∈DIt,j,k∈M

(25)

si,ri,jri∈{0,1},?i∈DIt

(26)

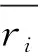
S-2階段滾動窗口中車輛數(shù)量為C1，且所有車輛經過一次決策全部登船配載，則S-2階段的決策模型為

SPMS-2(t){f1(t),f2(t):(7)～(20),

(27)

模型目標為式(5)～式(6)，約束條件為式(7)～式(20)和式(22)～式(27)，式(27)保證過渡階段剩余車輛全部裝船.

3 算法設計

3.1 多階段動態(tài)決策框架

針對配載的S-1階段設計首層和主體動態(tài)配載，并結合針對S-2、S-3、S-4階段設計的過渡、補充動態(tài)配載和延遲配載，形成多階段動態(tài)決策框架實現(xiàn)求解，見圖3.

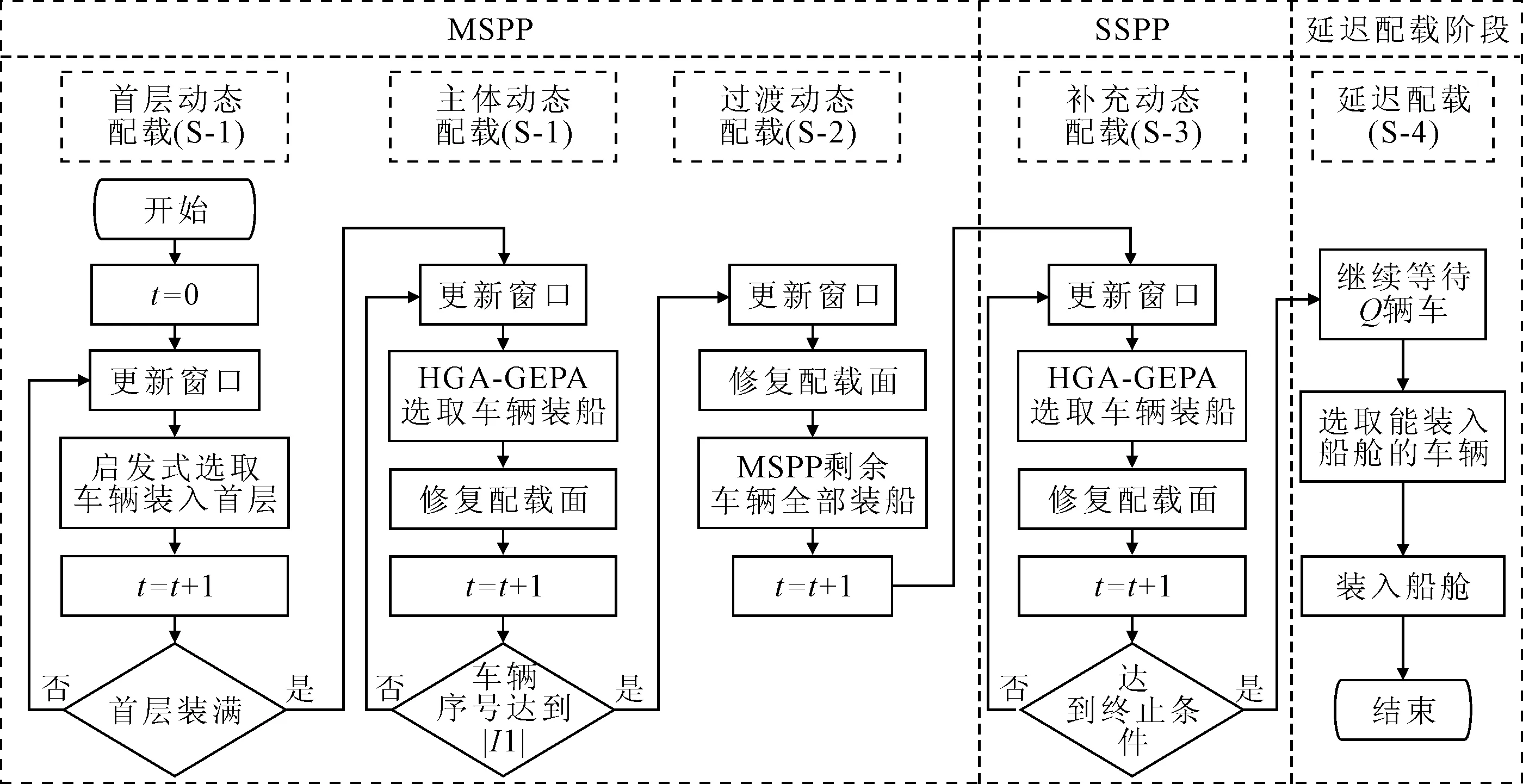
圖3 多階段動態(tài)決策框架

3.2 基于灰熵并行分析的混合遺傳算法

本文基于GA算法，融合GEPA方法，設計了HGA-GEPA，算法流程見圖4.

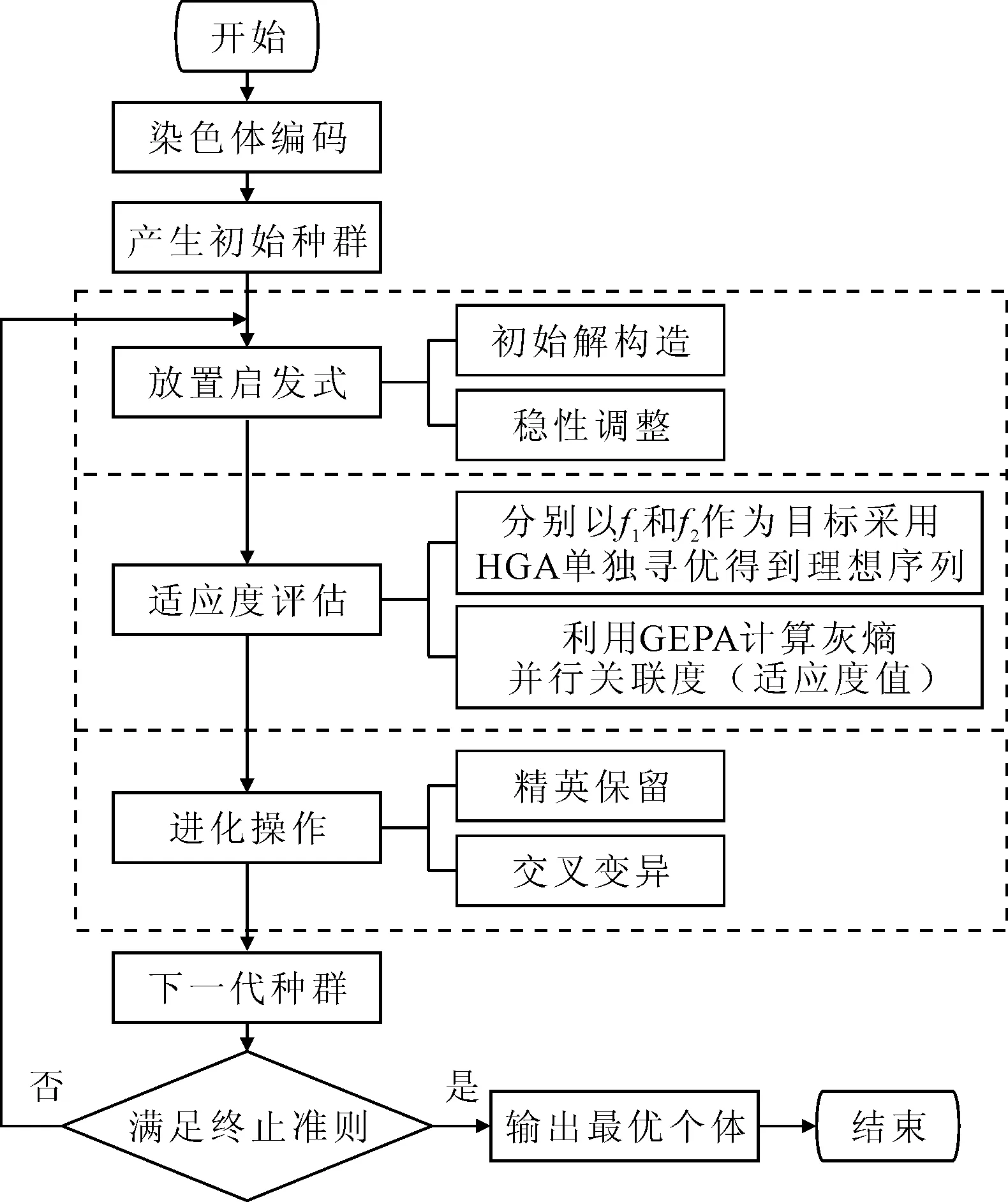
圖4 HGA-GEPA尋優(yōu)流程圖

染色體編碼見圖5.染色體長度對應滾動窗口長度，編碼采用隨機數(shù)編碼的方式分別排序，一個染色體表征一種裝船序列.

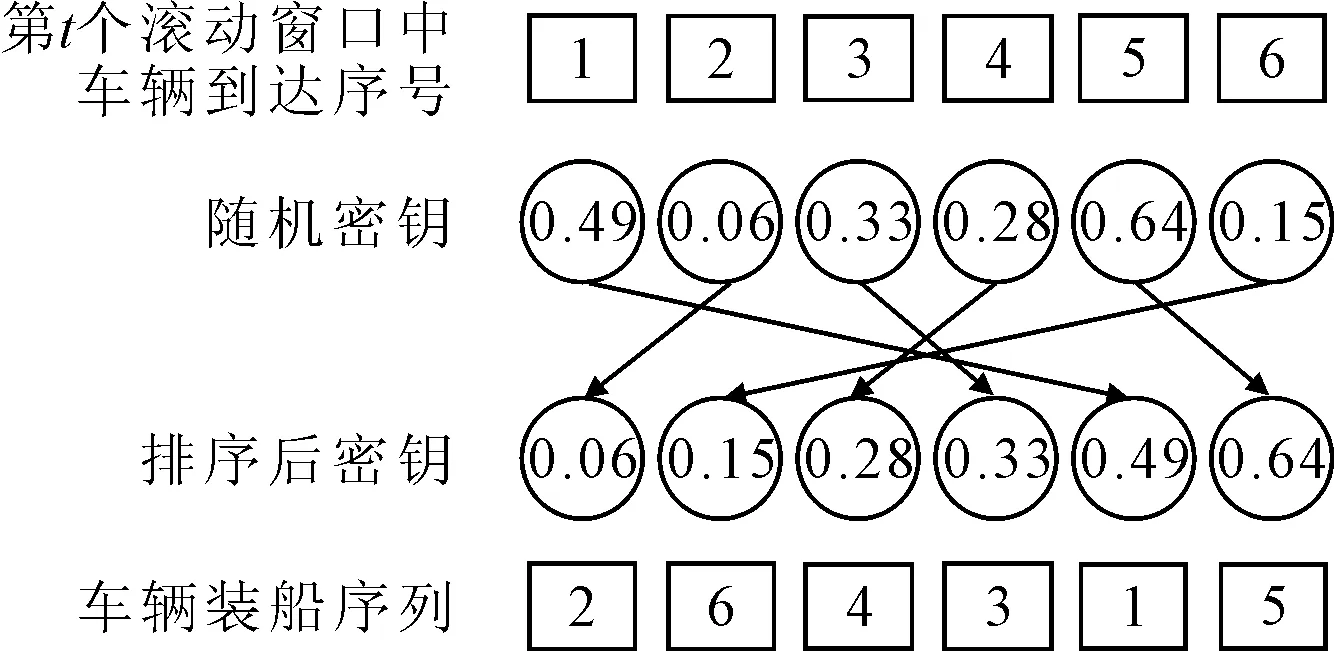
圖5 染色體編碼

放置啟發(fā)式需要得到滿足二維裝箱和穩(wěn)性等約束且效果良好的配載方案，是算法設計中的難點.本文的放置啟發(fā)式包括初始解構造和穩(wěn)性調整兩部分.

1) 初始解構造 為確定當前決策集中車輛在船艙中的擺放位置，本文利用文獻[1]多階段啟發(fā)式中的評分策略評判配載優(yōu)劣，生成初始解，見圖6.

圖6 基于評分策略的配載方案

2) 穩(wěn)性調整 為保證配載時橫傾處于較理想的范圍，沿y軸方向將船舶等分為左側和右側空間，當裝入車輛評分為0時，若此時橫傾小于0，則將車輛放置在船艙右側空間；反之放置在左側空間.

適應度評估是多目標決策算法的關鍵步驟，GEPA[9-10]是一種新穎的適應度評估方法，它將灰色理論和信息熵理論融合，以灰熵并行關聯(lián)度作為衡量多目標解與理想解相似度的依據(jù)，并將其作為適應度值指導算法進化.灰熵并行關聯(lián)度越大，表示當前解越接近于理想解，解的質量越好.本文以GEPA作為算法的適應度評估方法，優(yōu)化目標有2個.假設種群個數(shù)為P個，則GEPA步驟總結如下：

步驟1構造理想解序列 以GA對種群實現(xiàn)配載面高度最低和平滑度最高的多目標并行優(yōu)化，得到由2個目標函數(shù)優(yōu)化值組成的理想解(參考)序列Y0={f1(0),f2(0)}.

步驟2構造比較解序列 對當代種群中的任意個體j，j∈{1,2,…,P}，分別計算2個優(yōu)化目標的函數(shù)值，構成比較解序列Yj={f1(j),f2(j)}，進而得到種群的比較解序列Y={Y1,Y2,…,Yi,…,YP}.

步驟3灰關聯(lián)度分析 計算群體中任意個體的灰關聯(lián)度r(Y0,Yj)，j∈{1,2,…,P}.

步驟4熵值權重 計算比較解序列子目標的信息熵ei(j)和熵值權重Wj(i)，i∈{1,2}，j∈{1,2,…,P}.

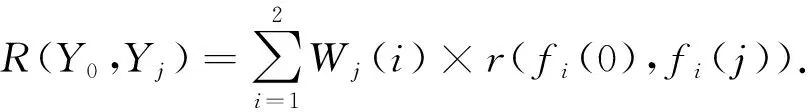
借鑒文獻[11]的偏隨機密鑰遺傳算法，通過復制、交叉和變異3種操作，各產生一定比例的群體構成下一代種群，見圖7.

圖7 進化操作

4 實驗設計與分析

4.1 算例設計

本文參照文獻[1]進行算例設計，選取兩艘典型客滾船作為實驗對象，并分為晚間(記為N)和日間(記為D)兩個場景，三種車輛均考慮多種車型，客滾船具體參數(shù)(見表1)和兩個場景下的車輛比例(見表2)，車輛類型和數(shù)據(jù)均與文獻[1]中應用實驗相同.為表明不同滾動窗口長度H和每次決策車輛數(shù)對配載結果的影響，設置若干組滾動窗口長度H和每次決策的車輛數(shù)(H的25%、50%和75%)，見表3.為保證待配載車輛數(shù)量與實際船艙可配載車輛之間的差距較小，將文獻[1]中p=0.9時確定的車輛數(shù)量作為此次實驗的待配載車輛數(shù)量，并以此形成待配載車輛發(fā)生源，模擬實際客滾船配載流程.

車輛重量按實際隨機生成，車輛間安全距離設為0.2 m.采用諸如A1-N-P1-S1的方式來表示不同算例，其中A1為船型；N為晚間作業(yè)場景；P1為車輛的比例；S1為決策窗口狀態(tài).每個配載決策長度下有24個算例，實驗共計72個算例.

表1 實驗客滾船信息

表2 實驗場景及其車輛比例

表3 決策窗口設計

為測試HGA-GEPA的性能，設計人工配載啟發(fā)式(Artificial Loading Heuristic，ALH)和常規(guī)HGA，將HGA-GEPA分別替換為ALH和常規(guī)HGA，作為對照組.ALH規(guī)則為：配載時先配船頭和兩側，再配船艙中間位置，優(yōu)先放置貨車，貨車留出的空隙放置小車.常規(guī)HGA的初始種群個數(shù)和迭代方式與HGA-GEPA一致，不同點在于常規(guī)HGA在迭代尋優(yōu)時遵循以下規(guī)則進行群體排序：所有個體首先按照f1的值升序排列，若f1值相同，則按照f2的值升序排列，位于前10%的為精英種群.

4.2 參數(shù)設置

每個算例運行10次取平均值，HGA-GEPA和HGA的種群大小設為50，當所求最優(yōu)解連續(xù)30代無改變或達到最大迭代次數(shù)100代時算法終止，精英保留率、交叉概率分別為0.1、0.7，隨機生成變異個體比例為20%.延遲驗收長度Q與配載決策長度H相等.GEPA方法中灰關聯(lián)分析分辨系數(shù)ρ=0.5.

4.3 應用實驗結果分析

以文獻[1]中對應算例的算法求解結果作為動態(tài)在線問題的上界(upper bound for dynamic online problems, UBDOP).表4為在H=8下應用不同算法求解三種船型算例的結果(由于篇幅問題H=12,16略去).基于ALH的多階段動態(tài)決策進行求解時由于單個滾動窗口決策時間太短，故此處T2不再列出.

表4 算例實驗結果(H=8)

隨著H的增大，三種算法求解結果均呈現(xiàn)上升趨勢，且與UBDOP的平均gap值呈現(xiàn)下降趨勢.主要原因在于當H增大，獲取的車輛信息量增大，信息的不確定性對于船舶配載的影響減弱.隨著H的增大，HGA和HGA-GEPA在整體求解時間上均有一定程度的上升.主要原因在于當H增大，決策維度明顯增大，導致尋優(yōu)收斂代數(shù)增加，收斂時間增加.圖8為三種H下，不同算法求解24個算例的船艙整體面積利用率折線圖.由圖8可知：對于三種H，HGA-GEPA求解結果較ALH和HGA均具有明顯的優(yōu)越性，且對于同一H，其每次決策車輛數(shù)與船艙面積利用率之間無明顯規(guī)律.

圖8 面積利用率結果分析

對于不同的H，HGA-GEPA平均求解結果均達到90%以上，平均gap值保持在6%左右，均優(yōu)于ALH和HGA，且單個決策窗口求解迅速，顯示算法具有較強的適用性、實時性和魯棒性.

5 結 束 語

文中針對客滾船配載作業(yè)的實時動態(tài)和二維裝箱等特點，設計了一種滾動推進策略，構建了以各決策階段的客滾船配載面高度最低和平滑度最高為目標函數(shù)的多目標在線配載決策模型.同時，鑒于復雜特性，設計了融合HGA-GEPA的多階段動態(tài)決策框架對問題進行求解，以HGA-GEPA確定各決策階段裝船車輛及其配載方案.對比實驗驗證了模型和多階段動態(tài)決策框架的有效性，且框架中的HGA-GEPA要優(yōu)于人工配載啟發(fā)式和常規(guī)HGA，可以實現(xiàn)配載方案的高效評估選擇，得到較優(yōu)的船艙面積利用率.