充液管路振動特性半解析建模及卡箍布局優化

張宇 ，孫偉 ，劉旭東

(1.東北大學 機械工程與自動化學院，遼寧 沈陽，110819；2.東北大學 航空動力裝備振動及控制教育部重點實驗室，遼寧 沈陽，110819)

航空發動機管路系統主要用于傳輸燃油、滑油等工作介質，是保證航空發動機可靠工作的重要附件系統。航空發動機外管路主要通過卡箍固定在機匣上，發動機內部的轉子或者氣流激勵會通過機匣傳遞到管路，當外激勵的頻率接近管路固有頻率時，管路系統會發生共振，從而大幅度增加管路的振動幅度[1-2]。過大的振動會導致管接頭裂紋、卡箍松動甚至斷裂等故障，嚴重影響航空發動機工作的安全性及可靠性，因而，需要采用有效的減振措施來控制管路的振動。卡箍的支撐剛度及阻尼等力學參數會對管路系統的動力學特性產生直接影響，采用調整卡箍布局使管路避開發動機的激振頻率被認為是一種最經濟、最有效的管路系統減振方法。

為了獲得最優的卡箍布局，需要執行管路系統的避振優化，而執行避振優化的前提是要創建一個合理的管路系統動力學分析模型。航空發動機中大部分管路處于充液狀態，因而需要研究充液管路的動力學建模與分析方法。目前，以航空發動機管路為對象進行充液管路動力學的研究較少，但是以輸油、輸氣和飛機液壓管路等為對象的充液管路動力學已有大量研究，其建模方法包括傳遞矩陣法[3-4]、有限元法[5-6]、特征線法[7-8]、半解析法等。在這些建模方法中，半解析法由于所需自由度少、計算效率高得到了較為廣泛的應用，如HUANG 等[9]根據Hamilton變分原理得到了輸液管路的振動方程，并采用消元Galerkin法求解了特殊邊界條件下輸液管路的固有頻率；初飛雪[10]根據Hamilton 原理推導了輸液管路的振動變分方程，采用直接解法求解了兩端簡支管路的固有頻率及臨界流速；LIANG 等[11]以Euler-Bernoulli梁模擬管路，采用微分求積法及Laplace 變換分析了充液管路的振動特性；LI 等[12]使用He's 變分迭代法對輸液管路進行了自由振動分析，得到了在不同邊界條件下管路的臨界流速和臨界頻率。現有的大部分管路系統半解析建模理論針對的是經典邊界條件下的管路，對于多卡箍支撐的管路結構并不適用，因此需對其重新進行半解析建模。

以減振為目標，一些學者針對管路系統卡箍布局優化開展了研究，例如ZHANG等[13]以調節管路固有頻率及動態響應最小化為優化目標，采用遺傳算法求解得到了最優的卡箍位置。李鑫等[14]采用粒子群優化算法，以系統特征阻抗最小為目標函數進行了卡箍的布局優化，實現了充液管路的減振。GAO 等[15]以管路基頻與激勵頻率差值最大及管路位移響應為優化目標，通過神經網絡建立優化的代理模型并使用遺傳算法進行求解，顯著降低了管路系統的振動。劉偉等[16]以基頻與激勵頻率差值最大化及隨機振動的響應均方差最小化為目標，使用罰函數法對管路系統的卡箍位置進行了優化。柳強等[17]以管路的1階和2階固有頻率為優化目標，使用Kriging 模型和NSGA-Ⅱ算法求解了最佳卡箍位置，大大提高了優化效率。TANG等[18]以卡箍位置為設計變量，以液壓管路的累計疲勞損傷失效概率作為優化目標，采用序列二次規劃法進行了求解，優化后顯著提升了管路的動力學性能。總的來看，目前對于管路的卡箍位置優化以空管為主，雖然也有一些針對充液管路的卡箍位置優化，但是并沒有明確液體參數對于充液管路卡箍布局優化結果的影響。

本文作者以多卡箍支撐充液管路為研究對象，采用半解析方法建立動力學模型，介紹建模的原理及流程。隨后根據航空發動機的實際工作情況，建立以1階固有頻率最大為優化目標，以卡箍位置為設計變量的優化模型并采用粒子群算法進行優化求解。最后，通過與文獻比對驗證了所建立的半解析模型的正確性，進一步以三卡箍充液管路為實例實施了卡箍布局優化研究，并分析了液體質量、流速以及管徑等對卡箍布局優化結果的影響。

1 多卡箍支承充液管路半解析建模

圖1所示為含有N個卡箍支撐的充液管路，其中，l為管路總長度，D和d分別為管的外徑和內徑，v為管內液體流速。由于充液管路含有多個卡箍支撐，因此屬于超靜定結構，為了完成其半解析建模，將該系統分為空管、卡箍、管內流體3個部分，每一部分單獨進行能量分析，最后再進行組合，最終推導出充液管路總的動力學方程。

圖1 多卡箍支撐充液管路模型Fig.1 Liquid-filled pipeline model with multi-clamp support

1.1 能量分析

管路系統的橫向位移w可表示為

式中：ω為管的振動頻率；φ為相位；W(x)為系統的振型函數，可表達為

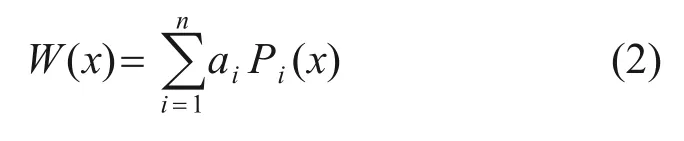
式中：ai為待定系數；Pi(x)為一系列特征多項式，可由Graham-Schmidt 正交化求得[19]，求解的基本過程如下：

對?k(x)進行歸一化處理可得：

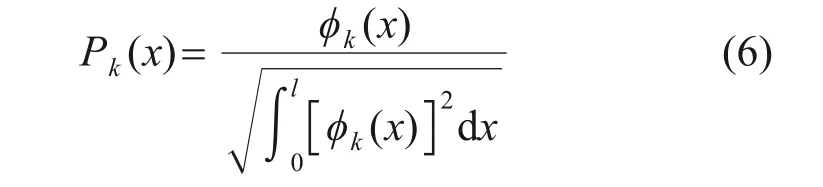
特征多項式Pi(x)滿足以下正交條件：

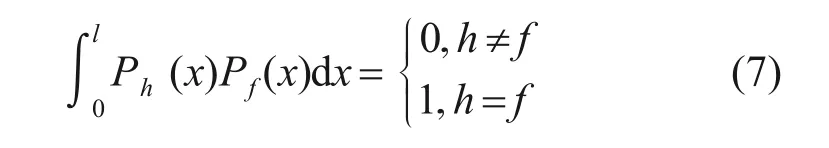
1.1.1 空管管體能量分析

由Euler-Bernoulli 梁理論，空管部分的勢能Vp和動能Tp分別為

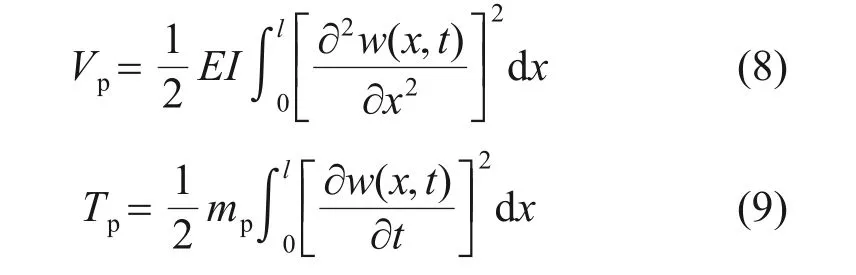
式中：EI為管的抗彎剛度；mp為管的單位長度質量。

在偏離平衡位置最遠處，管路具有最大勢能Vpmax，在靜平衡位置具有最大動能Tpmax，其表達式分別為

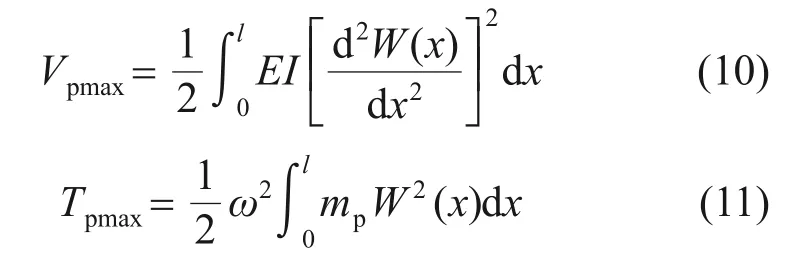
1.1.2 卡箍能量分析

參照已有的卡箍動力學建模[20-21]，卡箍可以用彈簧-阻尼單元來進行模擬，并忽略阻尼效應，將1 個卡箍等效為2 對彈簧單元，每對彈簧單元由1個線性彈簧和1個扭轉彈簧組成，卡箍部分的簡化模型如圖2所示，以管路的左端點為原點O，由原點向右為正方向，xk(k=1,2,…,2N)為第k對彈簧距原點O的距離，線性彈簧的支撐剛度為Kv，扭轉彈簧的扭轉剛度為Kθ，每個卡箍對應的彈簧剛度均相同。

圖2 卡箍簡化模型Fig.2 Simplified clamp model

位于xk處的彈簧對的勢能為

1.1.3 流體介質能量分析

設管內的液體流動速度恒為v，流體的單位長度質量為mf，則管內流體的動能Tf和最大動能Tfmax分別為

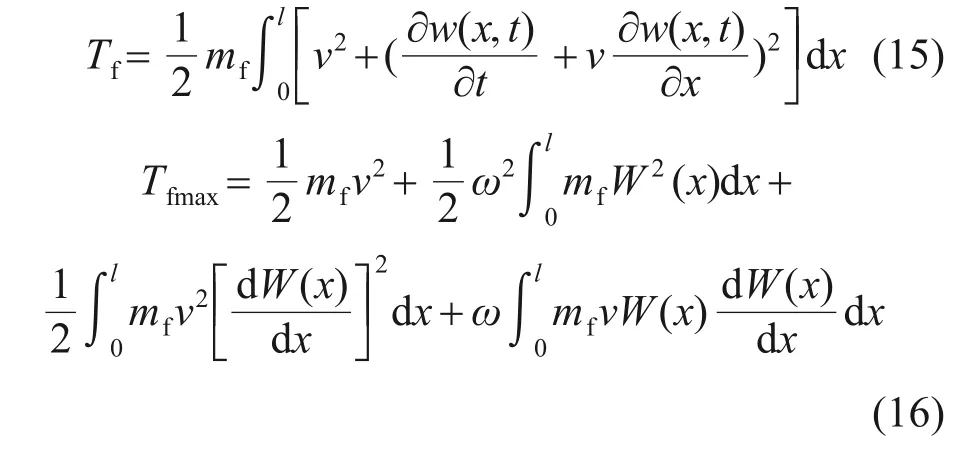
將空管、卡箍、流體的最大勢能和最大動能相加，得到多卡箍支撐充液管路的總勢能Vmax和總動能Tmax分別為

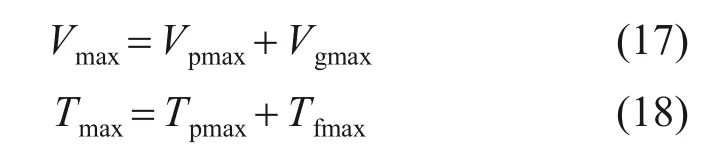
1.2 動力學模型

將式(2)分別代入式(10)，(11)，(13)和(16)中可得：

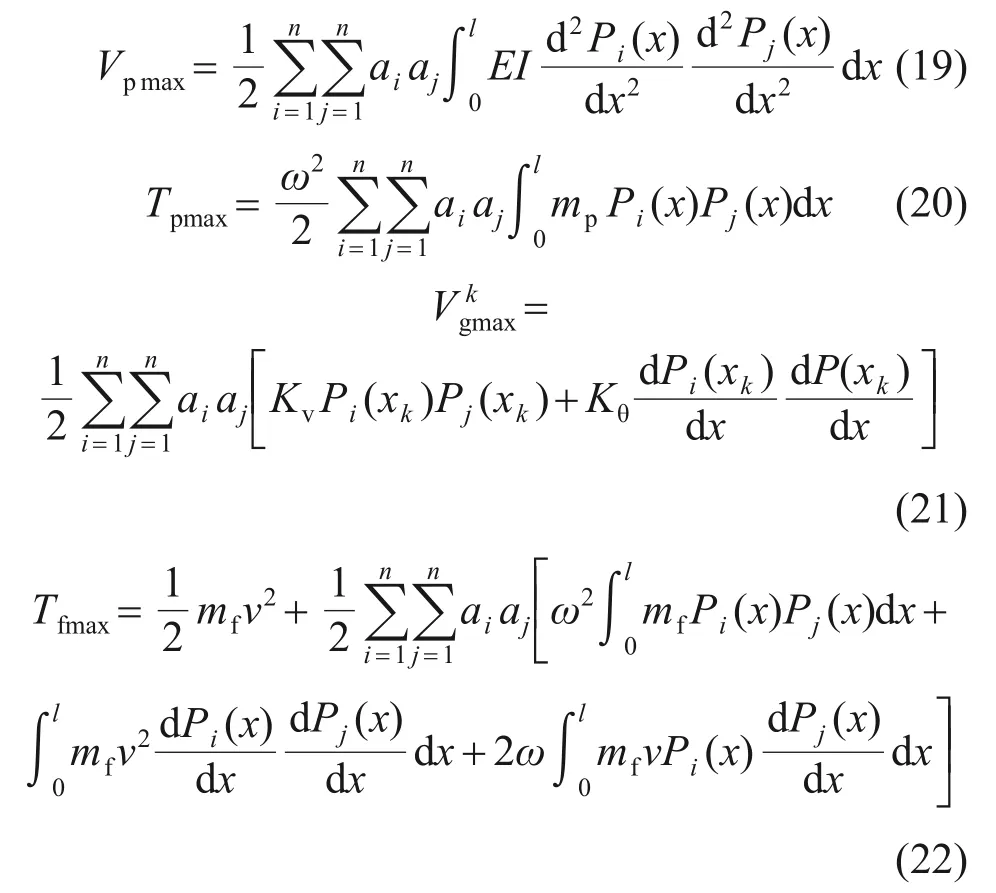
針對式(19)～(22)，設空管的剛度Kpij及質量Mpij、第k對彈簧的剛度、流體的剛度Kfij及質量Mfij分別為

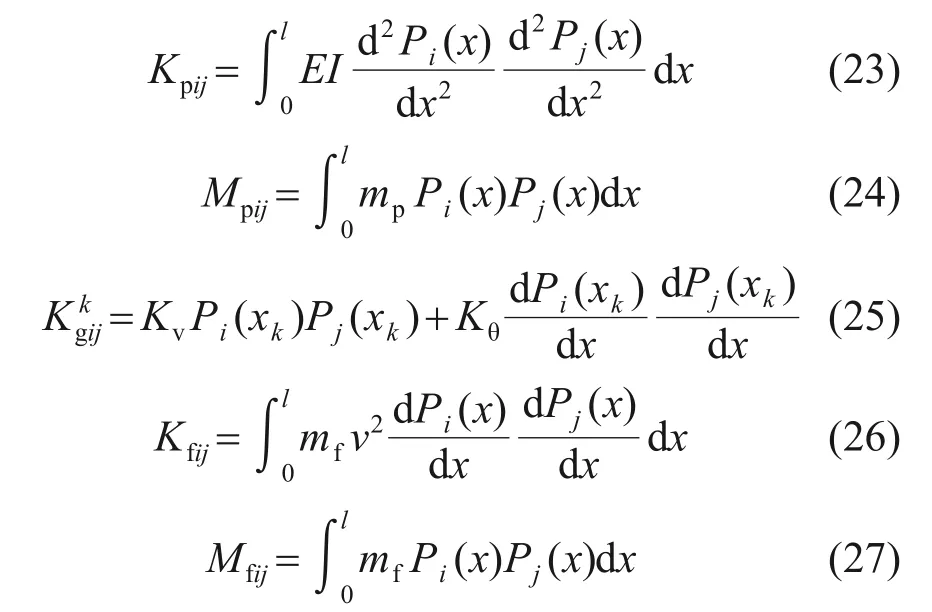
進一步，設I=Vpmax+Vgmax-Tpmax-Tfmax=Vmax-Tmax，利用拉格朗日方程

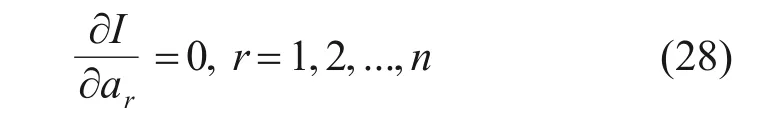
得到多卡箍支撐充液管路的動力學方程為

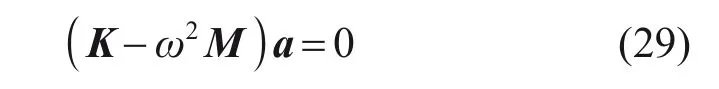
式中：K為剛度矩陣，K=Kp+Kg+Kf，Kp為空管管體的剛度矩陣，Kg為卡箍的剛度矩陣，Kf為流體的剛度矩陣；M為質量矩陣，M=Mp+Mf，Mp為管體的質量矩陣，Mp為流體的質量矩陣。

求解式(29)，可以得到多卡箍支撐充液管路的前n階固有頻率fr，其中，r=1，2，…，n。

2 多卡箍支承充液管路布局優化

為了進行多卡箍支撐充液管路卡箍的位置優化，首先需要建立合理的動力學優化模型，同時選擇合適的算法對模型進行求解。

2.1 優化模型

大部分管路剛性較大，因而在管路系統設計時，選擇管路系統1階固有頻率大于等于激振頻率的1.25 倍[22]，保證管路系統所有固有頻率避開激振頻率。這里選擇充液管路1階固有頻率f1最大為本文的優化目標。

設計變量示意圖見圖3，圖中，Di為第i個卡箍左端面與管路最左端的距離，其中i=1，2，…，N。以卡箍在管路中的位置Di為設計變量，根據相關設計標準的內容[23]，兩個卡箍之間存在最大距離的要求，卡箍不可能在管路上隨意布置，圖3中的虛線框區域為各個卡箍的允許布置區域，每個卡箍都有其移動的上下限，設Dli和Dui分別為第i個卡箍的移動下限及上限，即Dli≤Di≤Dui。

圖3 設計變量示意圖Fig.3 Schematic diagram of design variables

最終，建立的多卡箍支撐充液管路的卡箍布局優化模型為

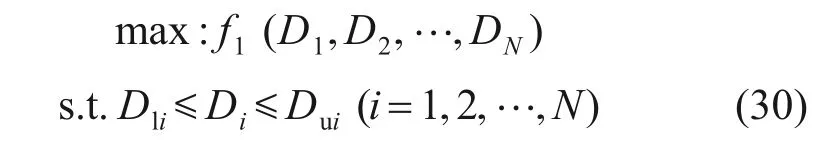
需要說明的是，為了研究充液狀態對卡箍布局優化結果的影響，在整個優化模型中，并未引入外界對管路的激振頻率。

2.2 優化求解

采用粒子群優化(particle swarm optimization,PSO)[24-25]對上述優化模型進行求解。粒子群優化算法中粒子、位置、速度、適應度、個體最優值、全局最優值等術語與本研究中卡箍布局優化模型之間的對應關系見表1。

表1 粒子群優化中的術語與卡箍布局優化的對應關系Table 1 Relationship between terms in PSO and clamp layout optimization

本研究的優化目標為多卡箍支撐充液管路的1階固有頻率最大，是單目標優化，根據粒子群算法的基本思想，充液管路卡箍布局優化的算法流程如下。

1) 初始化粒子。選擇Z組粒子，賦予每個粒子隨機的初始卡箍位置，組成初始的卡箍位置點集合，并賦予初始速度。

2) 計算適應度。根據給出的每組初始卡箍位置點信息(即一個粒子)分別計算其對應的充液管路的1階固有頻率。

3) 計算個體最優值。對每組卡箍位置點，將其當前得到的1階固有頻率與其先前迭代過程得到的個體最優值進行比較，若當前的1階固有頻率更大，則用當前的1階固有頻率取代其先前的個體最優值，成為新的個體最優值。

4) 計算全局最優值。對全部卡箍位置點(所有Z組粒子)，將當前得到的1階固有頻率與先前得到的全局最優值進行比較，若當前的1階固有頻率更大，則用當前的1 階固有頻率取代其全局最優值，成為新的全局最優值。

5) 更新粒子速度和位置。按照算法的迭代規則，由新的個體最優值和全局最優值得到新的卡箍位置點集合的位置及速度信息，準備進行下一次的迭代計算。

6) 判斷是否滿足中止條件。若滿足則輸出當前的全局最優值作為優化得到的最優值，并記錄其對應的卡箍位置點；若不滿足，則返回步驟2)，開始新一輪的計算。

3 實例研究

以三卡箍支撐充液直管為例，對其進行半解析建模以及實施充液管路卡箍布局優化，充液直管的管長l=500 mm，外徑D=8 mm，內徑d=6.4 mm，彈性模量E=1.99×1011Pa，管材密度ρp=7 850 kg/m3，泊松比μ=0.3，管內液體密度ρf=1 000 kg/m3，用于模擬卡箍的線性彈簧的剛度Kv=4.3×105N/m，扭轉彈簧的剛度Kθ=80 N·m/rad，3個卡箍的剛度相同，卡箍的寬度為14 mm。

3.1 模型正確性校驗

文獻[5]使用有限元法求解管路的固有特性，以文獻[5]中的充液懸臂管為對象驗證所建立的半解析模型的準確性，懸臂管模型[5]如圖4所示，懸臂管長度l為1 010 mm，外徑D為22.85 mm，內徑d為19.65 mm，管材密度為2 800 kg/m3，彈性模量為70 GPa，泊松比為0.3，管內液體密度為1 000 kg/m3。當管內液體速度v=10 m/s時，充液懸臂管的前4階固有頻率如表2所示。

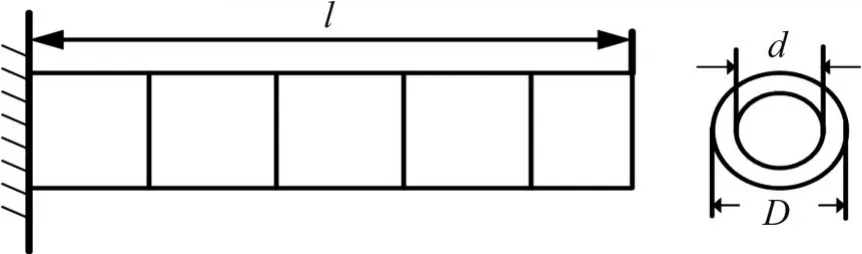
圖4 充液懸臂管模型[5]Fig.4 Liquid-filled cantilever pipeline model[5]

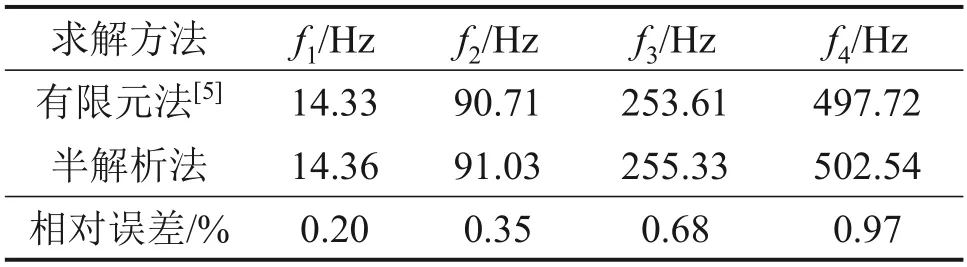
表2 充液懸臂管各階固有頻率Table 2 Natural frequencies of liquid-filled cantilever pipe

由表2可以看出，采用有限元法得到的該充液懸臂管模型的前4階固有頻率與本文采用半解析法建模得到的前4階固有頻率差別較小，證明了本文采用半解析法建模求解充液管路固有頻率的準確性。

3.2 振動特性分析

三卡箍支撐充液直管模型如圖5 所示，3 個卡箍在管路上的初始位置分別為D1=75 mm，D2=250 mm 和D3=425 mm，管內液體以速度v勻速流動。

圖5 三卡箍支撐充液管路Fig.5 Three-clamp support liquid filling pipeline

在考慮流體作用時，設置流速分別為0，2，5和10 m/s 的工況。在不同流速下空管及充液直管前3階固有頻率如表3所示。

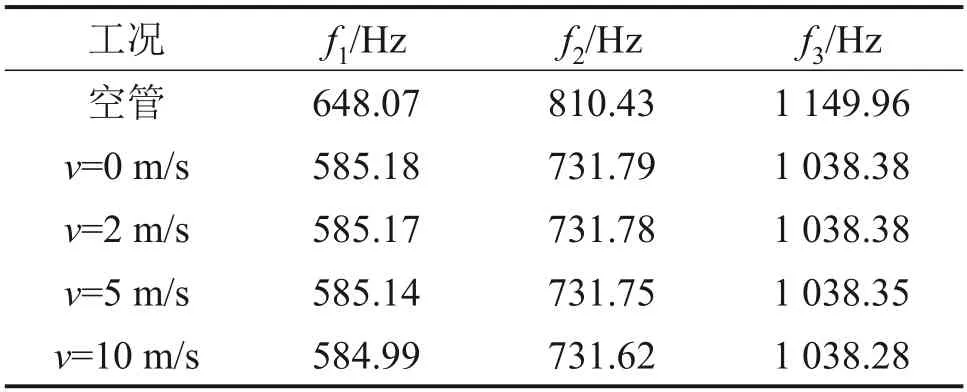
表3 空管及充液管路固有頻率對比Table 3 Comparison of natural frequencies of empty pipe and liquid-filled pipe

由表3可以看出，由于液體質量的影響，充液管路的各階固有頻率相比空管的下降較大；隨著流速增大，在考慮的速度范圍內，各充液管路的各階固有頻率變化較小。可見，在低流速下狀態下計算充液管路的固有頻率時，可忽略液體流速的影響，只需要考慮液體質量的影響，將液體質量視為管路的附加質量進行計算。

3.3 優化求解

以三卡箍支撐充液管路的1階固有頻率f1最大為優化目標，采用粒子群優化算法對充液管路的卡箍位置進行優化，設置粒子群算法中的各項參數如下：粒子數Z=50、最大迭代次數T=100，各個卡箍的允許布置范圍為Dl1=2 mm、Du1=150 mm、Dl2=170 mm、Du2=316 mm、Dl3=336 mm、Du3=484 mm。先針對空管，驗證優化算法的有效性，設優化前的卡箍位置為D1=75 mm，D2=250 mm 和D3=425 mm，計算其1階固有頻率，再使用粒子群優化算法對該空管模型進行卡箍位置優化，優化結果如表4所示。

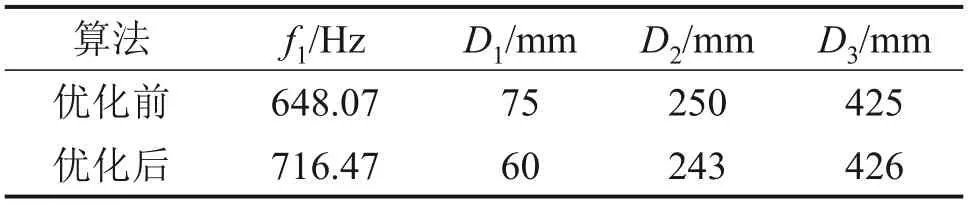
表4 空管優化前后結果對比Table 4 Comparison of results before and after optimization for empty pipeline

由表4可以看出，采用粒子群優化算法對管路卡箍位置進行優化后，管路的1階固有頻率提升了約68 Hz，驗證了所采用的粒子群優化算法的有效性。

優化過程中1階固有頻率的變化及優化進程如圖6 所示。從圖6 可以看出，當計算到第10 代時，結果開始收斂并得到最優值。

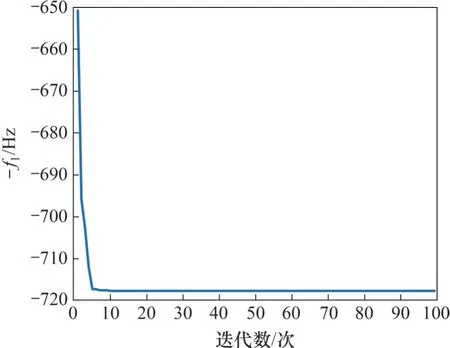
圖6 1階固有頻率優化迭代過程Fig.6 Optimize iterative process of the first-order natural frequency

3.3.1 充液對優化結果的影響

將空管的優化結果與流速為2 m/s 狀態下充液管路的優化結果進行對比，2組管路優化前的卡箍位置均為D1=75 mm，D2=250 mm 和D3=425 mm，管路優化結果如表5所示。

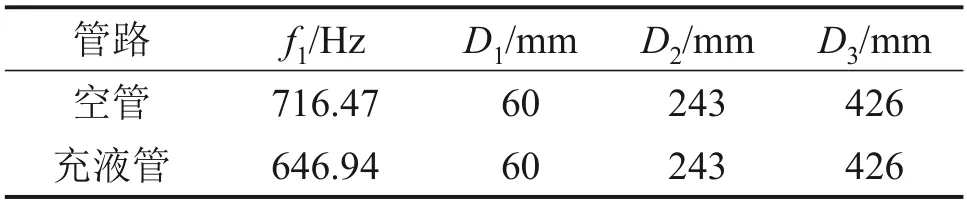
表5 空管及充液管路的優化結果Table 5 Optimization results of pipeline under condition of empty and liquid filled

由表3 和表5 可知，充液管路優化后的1 階固有頻率提升了約63 Hz，與表4 對比可知，空管和充液管路的優化效果相差不大。與振動分析結果相似，充液管路系統卡箍位置優化的目標函數值也顯著減小。但是對于設計變量最優值來說，空管及充液管路的最佳卡箍位置是相同的，說明充液與否對卡箍布局優化結果沒有影響。

3.3.2 流速對優化結果的影響

為了研究管內流體速度變化對于優化結果的影響，設置流速分別為0，2，5和10 m/s，不同流速工況下優化后的管路系統的1階固有頻率及最佳卡箍位置如表6所示。

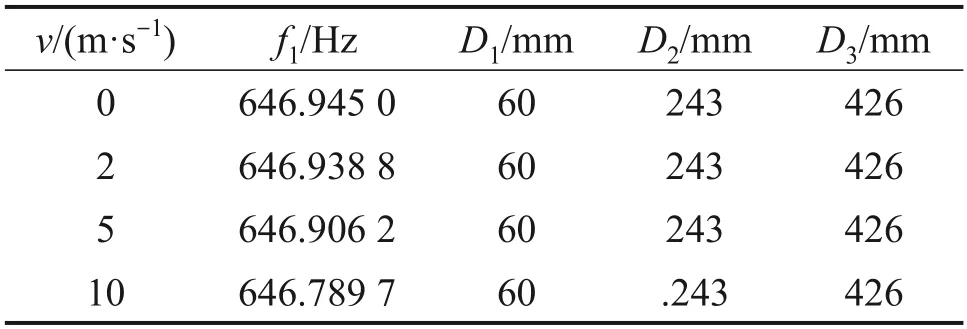
表6 不同流速下充液管路的優化結果Table 6 Optimization results of pipeline filled liquid at different flow rates

由表6可以看出，當管內流體速度增大時，管路系統優化后的目標函數值略微減小，這與3.2節振動分析的結果是一致的。但是，各個流速狀態下優化后的設計變量最優值是相同的，也即卡箍布局優化結果相同。綜上可認為管內流體速度對充液管路卡箍位置優化的目標函數值略有影響，在低速狀態下，可認為目標函數值基本不變，而對卡箍布局最優值完全沒有影響。

3.3.3 管徑對優化結果的影響

為了分析管徑對優化結果的影響，設置管徑分別為8，10，12，14和16 mm的直管，其余參數均相同，5 組管路均在流速2 m/s 下進行卡箍位置優化，優化結果如表7所示。

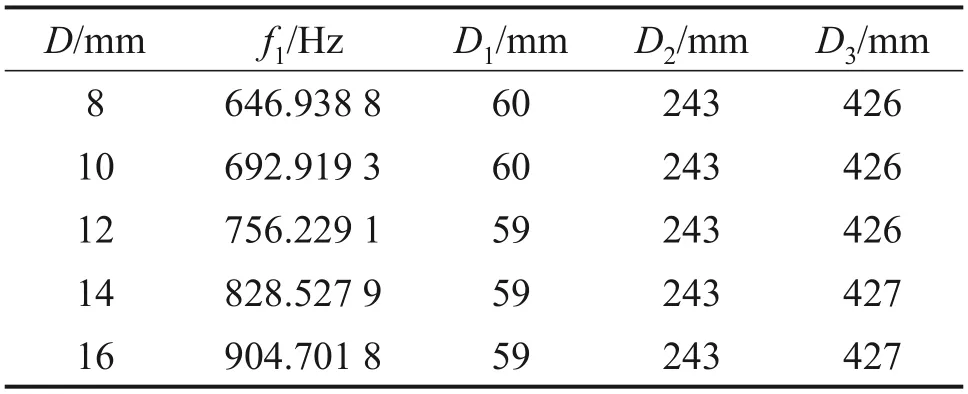
表7 不同管徑管路的優化結果Table 7 Optimization results of pipeline with different pipe diameters

由表7可以看出，優化后的目標函數值隨著管徑的增大而增大，這主要是因為管型的變化導致的，但是各個管徑的設計變量最優值基本相同，僅相差約1 mm，考慮到實際管路安裝中的誤差，偏差可以忽略不計。

綜合以上結果分析可知：1) 若僅以最大1階固有頻率為優化目標，則可以不考慮管路中的液體，僅以空管動力學模型為基礎模型進行優化，不影響卡箍布局優化結果；2) 若要考慮管路的1階固有頻率遠離激振頻率的程度，則必須以充液管路為基礎模型進行卡箍布局優化；3) 在進行充液管路的卡箍布局優化時，在低速狀態下，可以不考慮流速的影響，而僅將液體視為附加質量；4) 對于管型相同僅管徑不同的管路，若僅以最大1階固有頻率為優化目標，則可以忽略管徑的影響。

4 結論

1) 提出多卡箍支撐充液管路的半解析建模方法有效模擬充液管路的振動特性，并建立了通用的優化模型。以卡箍的支撐位置為設計變量，以充液管路1階固有頻率f1最大為優化目標，采用粒子群優化算法對該優化模型進行求解，該算法可快速獲得不同工況下卡箍布局優化的最優解。

2) 若僅以最大1階固有頻率為優化目標，則可以不考慮管路中的液體，而僅以空管動力學模型為基礎模型執行卡箍布局優化；若要考慮管路1階固有頻率遠離激振頻率的程度，則必須以充液管路為基礎模型進行優化。

3) 在對充液管路的卡箍布局進行優化時，在低速狀態下，可以不考慮流速的影響。

4) 當管路的管型相同僅管徑不同時，在僅以最大1階固有頻率為優化目標的前提下，可忽略管徑的影響。