基于正截面承載力及撓度控制的單筋矩形截面梁設(shè)計(jì)
徐 壯,蘇麗梅,張瑞剛
(1.長(zhǎng)江水利委員會(huì) 河湖保護(hù)與建設(shè)運(yùn)行安全中心,湖北 武漢 430014; 2.重慶市萬(wàn)盛經(jīng)濟(jì)技術(shù)開(kāi)發(fā)區(qū)交通局,重慶 400800)
0 引 言
當(dāng)梁截面尺寸及縱向配筋參數(shù)均未知時(shí),傳統(tǒng)設(shè)計(jì)方法是先憑借梁高跨比經(jīng)驗(yàn)取值假定截面高度,再根據(jù)GB 50010-2010《混凝土結(jié)構(gòu)設(shè)計(jì)規(guī)范》(以下簡(jiǎn)稱(chēng)《規(guī)范》)的相關(guān)公式進(jìn)行縱向受力鋼筋面積計(jì)算及撓度驗(yàn)算。對(duì)于單筋矩形截面梁,由于傳統(tǒng)方法不能主動(dòng)控制梁截面混凝土受壓區(qū)高度,往往會(huì)出現(xiàn)少筋梁或超筋梁的現(xiàn)象,還可能不滿足撓度驗(yàn)算要求,因而需重復(fù)設(shè)計(jì),過(guò)程繁瑣且不直觀。張會(huì)平[1]推導(dǎo)了單筋受彎構(gòu)件正截面配筋設(shè)計(jì)的簡(jiǎn)化計(jì)算公式;張立人等[2]提出利用弦桿法簡(jiǎn)化計(jì)算混凝土受彎構(gòu)件正截面承載力;曾彬峻等[3]利用罰函數(shù)法對(duì)鋼筋混凝土梁的截面尺寸和鋼筋用量進(jìn)行了優(yōu)化設(shè)計(jì);張鵠志等[4]對(duì)不同荷載工況下的鋼筋混凝土深梁開(kāi)展了拓?fù)鋬?yōu)化設(shè)計(jì)研究。Aschheim等[5]提出了一種用于單軸或雙軸彎曲的梁、柱和墻截面配筋設(shè)計(jì)的直接計(jì)算方法。
《規(guī)范》提倡采用HRB400和HRB500作為梁的縱向受力普通鋼筋,并規(guī)定當(dāng)采用強(qiáng)度等級(jí)為400 MPa及以上的鋼筋時(shí),混凝土強(qiáng)度等級(jí)不應(yīng)低于C25。因此,本文主要探討以下不同強(qiáng)度等級(jí)的材料組合情況:① 縱筋采用HRB400,混凝土等級(jí)為C25、C30及C35;② 縱筋采用HRB500,混凝土等級(jí)為C30、C35及C40。當(dāng)梁的縱向配筋率取經(jīng)濟(jì)配筋率[6-7]ρ∈[0.6%,1.5%],縱筋及混凝土采用以上組合時(shí)均為適筋梁。
本文將《規(guī)范》相關(guān)公式進(jìn)行簡(jiǎn)化,在縱向受力鋼筋取經(jīng)濟(jì)配筋率的條件下,推導(dǎo)出滿足正截面承載力要求的梁截面高度計(jì)算公式。同時(shí),通過(guò)簡(jiǎn)化得出短期剛度系數(shù)的表達(dá)式,進(jìn)而推導(dǎo)出由撓度驗(yàn)算控制的梁截面高度計(jì)算公式。綜合正截面承載力及撓度驗(yàn)算雙重控制計(jì)算所得的結(jié)果,即可簡(jiǎn)單便捷地確定合理的梁截面高度。
1 正截面承載力控制的梁高度計(jì)算公式
根據(jù)《規(guī)范》,對(duì)于適筋情況下的單筋矩形截面梁,其正截面承載力計(jì)算公式為
α1fcbx=fyAs
(1)
(2)
式中:α1為fc的調(diào)節(jié)系數(shù),當(dāng)混凝土強(qiáng)度等級(jí)不超過(guò)C50時(shí),α1取1.0,當(dāng)混凝土強(qiáng)度等級(jí)為C80時(shí),α1取0.94,其間按線性內(nèi)插法確定;fc,fy分別為混凝土軸心抗壓強(qiáng)度設(shè)計(jì)值和鋼筋抗拉強(qiáng)度設(shè)計(jì)值;b為梁的截面寬度;x為混凝土受壓區(qū)高度;As為受拉區(qū)縱向鋼筋的截面面積;M,Mu分別為梁的彎矩設(shè)計(jì)值和正截面受彎承載力設(shè)計(jì)值;h0為截面有效高度,h0=h-as,其中h為梁截面高度,as為全部縱向受拉鋼筋合力作用點(diǎn)至截面近邊緣的距離。
聯(lián)立式(1)、(2)得
(3)
將梁的縱向受拉鋼筋配筋率ρ=As/bh0代入式(3),根據(jù)h0=h-as,取h0≈0.93h[8-9],則:
(4)
由式(4)可得
(5)
(6)
上述式中:梁的截面寬度b按構(gòu)造要求確定;當(dāng)梁的縱向受拉鋼筋配筋率ρ∈[0.6%,1.5%]時(shí),截面高度系數(shù)α與配筋率ρ的關(guān)系如圖1所示。

圖1 截面高度系數(shù)α與配筋率ρ的關(guān)系曲線Fig.1 Relation between section height coefficient α and reinforcement ratio ρ
由圖1可知,當(dāng)縱筋的強(qiáng)度等級(jí)相同,而混凝土的強(qiáng)度等級(jí)不同時(shí),各曲線非常接近。經(jīng)比較,忽略混凝土強(qiáng)度等級(jí)差異的誤差變化范圍為1.3%~4.1%,能滿足工程設(shè)計(jì)的精度要求。
當(dāng)ρ=1%時(shí),截面高度系數(shù)α的偏上限取值為① 采用HRB400級(jí)鋼筋時(shí),α=0.616;② 采用HRB500級(jí)鋼筋時(shí),α=0.561。結(jié)合式(6)及圖1的變化趨勢(shì),并引入配筋率影響系數(shù)η,得到梁截面高度的偏上限取值表達(dá)式如下。
梁的縱筋采用HRB400級(jí)鋼筋時(shí):
(7)
梁的縱筋采用HRB500級(jí)鋼筋時(shí):
(8)
式中:當(dāng)ρ=1%時(shí),η=1.0;當(dāng)ρ=0.6%時(shí),η=1.247;當(dāng)ρ=1.5%時(shí),η=0.856;其他配筋率時(shí)根據(jù)式(9)依次進(jìn)行線性插值。
η=0.856+43.44×(1.5%-ρ)
(9)
2 撓度控制的梁高度計(jì)算公式
《規(guī)范》規(guī)定:進(jìn)行普通鋼筋混凝土受彎構(gòu)件的撓度驗(yàn)算時(shí),應(yīng)采用荷載準(zhǔn)永久組合計(jì)算。在余先聲、張京穗等[8-9]的研究基礎(chǔ)上,設(shè)K=Mq/M。其中:Mq為按荷載準(zhǔn)永久組合計(jì)算的彎矩值,M為彎矩設(shè)計(jì)值;具體計(jì)算見(jiàn)GB 50009-2012《建筑結(jié)構(gòu)荷載規(guī)范》及《實(shí)用建筑結(jié)構(gòu)靜力計(jì)算手冊(cè)》[10]。
設(shè)梁的短期剛度為Bs,單位為N·mm2,對(duì)于單筋矩形截面梁,根據(jù)《規(guī)范》有:
(10)
式中:Es,Ec分別為鋼筋和混凝土的彈性模量,N/mm2;ψ為裂縫間縱向受拉鋼筋應(yīng)變不均勻系數(shù)。令梁短期剛度Bs=βsEcI,其中截面慣性矩I=bh3/12,βs為梁的短期剛度系數(shù)。經(jīng)公式轉(zhuǎn)換可得
(11)
根據(jù)《規(guī)范》,鋼筋牌號(hào)為HRB400時(shí)Es=2.0×105N/mm2,fy=360 N/mm2;鋼筋牌號(hào)為HRB500時(shí)Es=2.0×105N/mm2,fy=435 N/mm2;C25,C30,C35和C40的Ec分別取2.80×104,3.00×104,3.15×104N/mm2和3.25×104N/mm2,相應(yīng)ftk分別取1.78,2.01,2.20 N/mm2和2.39 N/mm2,fc分別取11.9,14.3,16.7 N/mm2和19.1 N/mm2。根據(jù)本文中的幾種不同強(qiáng)度等級(jí)材料組合情況,將上述參數(shù)代入式(11)得到相應(yīng)短期剛度系數(shù)βs的具體表達(dá)式如下。
梁的縱筋采用HRB400級(jí)鋼筋時(shí):
(12)
梁的縱筋采用HRB500級(jí)鋼筋時(shí):
(13)
根據(jù)《規(guī)范》規(guī)定:?jiǎn)谓罹匦谓孛媪翰捎煤奢d準(zhǔn)永久組合并考慮荷載長(zhǎng)期作用影響時(shí),其剛度應(yīng)按式(14)計(jì)算。
B=Bs/2
(14)
式中:B為矩形截面梁按荷載準(zhǔn)永久組合計(jì)算并考慮荷載長(zhǎng)期作用影響的剛度。
以承受均布荷載兩端簡(jiǎn)支的單筋矩形截面梁為例,當(dāng)采用荷載準(zhǔn)永久組合時(shí),滿足撓度驗(yàn)算要求的梁截面高度計(jì)算公式如下。
(15)
式中:f,flim分別為梁跨中撓度和撓度限值;Mq為按荷載準(zhǔn)永久組合計(jì)算的彎矩值;l0為梁的計(jì)算跨度。由式(15)可得
(16)
對(duì)于承受集中荷載或其他支承條件的情況,可根據(jù)具體條件計(jì)算相關(guān)參數(shù),參考上述算式推導(dǎo)出相應(yīng)的計(jì)算公式。
3 計(jì)算公式應(yīng)用
3.1 應(yīng)用步驟
(1) 按構(gòu)造要求確定梁截面寬度b,并在經(jīng)濟(jì)配筋率即[0.6%,1.5%]范圍內(nèi),選定縱筋配筋率ρ。
(2) 將配筋率ρ代入式(9),計(jì)算得到η。
(2) 根據(jù)式(7)或式(8)計(jì)算得到滿足正截面承載力要求的梁截面最小高度hmin1。
(3) 根據(jù)K=Mq/M,計(jì)算K值。
(4) 將K值及選定的配筋率ρ代入式(12)或式(13),求得短期剛度系數(shù)βs,再將相關(guān)參數(shù)代入式(16),可得由撓度驗(yàn)算控制的梁截面最小高度hmin2。
(5) 取hmin=max{hmin1,hmin2},并考慮模數(shù)要求,從而可確定能同時(shí)滿足正截面承載力及撓度要求的梁截面高度h。
(6) 取h0≈0.93h,可根據(jù)As=ρbh0求出縱向受力鋼筋的面積。
3.2 算例驗(yàn)證
3.2.1 算例1
簡(jiǎn)支矩形截面梁混凝土強(qiáng)度等級(jí)為C25,采用HRB400級(jí)鋼筋,混凝土保護(hù)層c=25 mm,承受均布荷載,梁的計(jì)算跨度l0=6.0 m。跨中彎矩設(shè)計(jì)值M=81.2 kN·m,按荷載效應(yīng)準(zhǔn)永久組合計(jì)算的Mq=41.7 kN·m,撓度限值flim=l0/250。
3.2.1.1 按本文方法設(shè)計(jì)
設(shè)梁截面寬度b=200 mm,基于隨機(jī)數(shù)學(xué)理論方法,利用隨機(jī)函數(shù)RAND在經(jīng)濟(jì)配筋率[0.6%,1.5%]范圍內(nèi)隨機(jī)生成2個(gè)ρ值,分別為1.29%、0.88%。
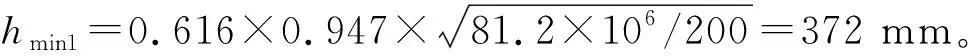



3.2.1.2 按《規(guī)范》公式驗(yàn)算


3.2.2 算例2
簡(jiǎn)支矩形截面梁混凝土強(qiáng)度等級(jí)為C35,采用HRB500級(jí)鋼筋,混凝土保護(hù)層c=25 mm,承受均布荷載,梁的計(jì)算跨度l0=6.5 m。跨中彎矩設(shè)計(jì)值M=130 kN·m,按荷載效應(yīng)準(zhǔn)永久組合計(jì)算的Mq=60 kN·m,撓度限值flim=l0/250。
3.2.2.1 按本文方法設(shè)計(jì)
設(shè)梁截面寬度b=200 mm,基于隨機(jī)數(shù)學(xué)理論方法,利用隨機(jī)函數(shù)RAND在經(jīng)濟(jì)配筋率[0.6%,1.5%]范圍內(nèi)隨機(jī)生成2個(gè)ρ值,分別為1.08%、0.75%。



經(jīng)計(jì)算,K=60/130=0.462,由式(13)得βs=0.388,又已知Ec=3.15×104N/mm2,flim=26 mm,將相關(guān)參數(shù)代入式(16),可得hmin2=464 mm。

3.2.2.2 按《規(guī)范》公式驗(yàn)算


4 結(jié) 論
(1) 本文在滿足正截面承載力及撓度驗(yàn)算要求的基礎(chǔ)上,推導(dǎo)了用以確定縱筋配筋率ρ∈[0.6%,1.5%]時(shí)的單筋矩形截面梁截面高度的簡(jiǎn)化公式,克服了傳統(tǒng)方法憑經(jīng)驗(yàn)取值的不足。通過(guò)選取配筋率ρ值并將其他已知參數(shù)代入相應(yīng)的公式,即可得到符合要求的梁截面尺寸及縱向配筋量。
(2) 該方法能主動(dòng)控制截面混凝土受壓區(qū)高度,有利于設(shè)計(jì)的優(yōu)化,且不需再驗(yàn)算是否出現(xiàn)少筋梁或超筋梁情況,也避免了撓度驗(yàn)算的繁瑣過(guò)程。同時(shí),梁的延性在經(jīng)濟(jì)配筋率范圍內(nèi)能夠得到保證。
(3) 由于選配鋼筋時(shí),梁的實(shí)際配筋量一般會(huì)略大于計(jì)算配筋量,因而可有效保證設(shè)計(jì)結(jié)果滿足要求;但若出現(xiàn)不能滿足裂縫寬度要求的情況,則需適當(dāng)增大配筋量或調(diào)整鋼筋直徑大小。
(4) 對(duì)于承受集中荷載或其他支承條件的單筋矩形截面梁,則根據(jù)具體情況計(jì)算彎矩值,將相關(guān)參數(shù)代入相應(yīng)的撓度計(jì)算公式,同樣可通過(guò)類(lèi)似方法推導(dǎo)出滿足撓度驗(yàn)算要求的截面高度計(jì)算表達(dá)式。

