美英早期幾何教科書中與圓有關的角
劉夢哲 汪曉勤
(華東師范大學教師教育學院 200062)
1 引言
圓心角、圓周角和弦切角的概念及相關定理是“圓”一章的重要內容,深刻揭示了圓中的弧、弦、角之間的關系.《義務教育數學課程標準(2022年版)》指出,要求學生理解圓、弧、弦、圓心角、圓周角的概念,了解等圓、等弧的概念;探索圓周角與圓心角及其所對弧的關系,了解并證明圓周角定理及其推論[1].
在已有的教學設計中,張安軍基于學生所學習過的垂徑定理,從圓的軸對稱性引出圓的旋轉對稱性,從而探究弧、弦、圓心角之間的關系[2].高建成基于學科大概念對圓周角的教學進行重構,由圓心角類比圓周角,由此形成定義,從分類討論中提煉模型,由此證明定理[3].林秋華在圓周角定義的基礎上,得到弦切角的定義,并從動態的角度引導學生發現、歸納得到弦切角定理[4].可見,在實際教學中,教師會讓學生通過觀察,給出圓心角、圓周角和弦切角的定義;通過探究圓的旋轉不變性,發現弧、弦、圓心角之間的關系;通過分類討論并利用三角形外角定理,證明圓周角定理.
HPM視角下的數學教學對于學生理解知識、掌握技能以及增進對數學過程與方法的理解起到了十分重要的作用[5].然而,手頭無史料卻成為阻礙教師在教學過程中開展HPM實踐的一大原因.教師對圓心角、圓周角和弦切角的歷史知之甚少,相關的HPM課例付之闕如.鑒于此,本文聚焦圓心角、圓周角和弦切角,對美英早期幾何教科書進行考察,希望從中獲得恰當的教學素材和思想啟迪,為今后的課例研究提供參考.
2 早期教科書的選取
本文選取1829—1948年間出版的87種美英早期幾何教科書作為研究對象,以20年為一個時間段進行劃分,其出版時間分布情況如圖1所示.其中,對于同一作者再版的教科書,若內容無顯著變化,則選取最早的版本,若內容有顯著變化,則將其視為不同的教科書.
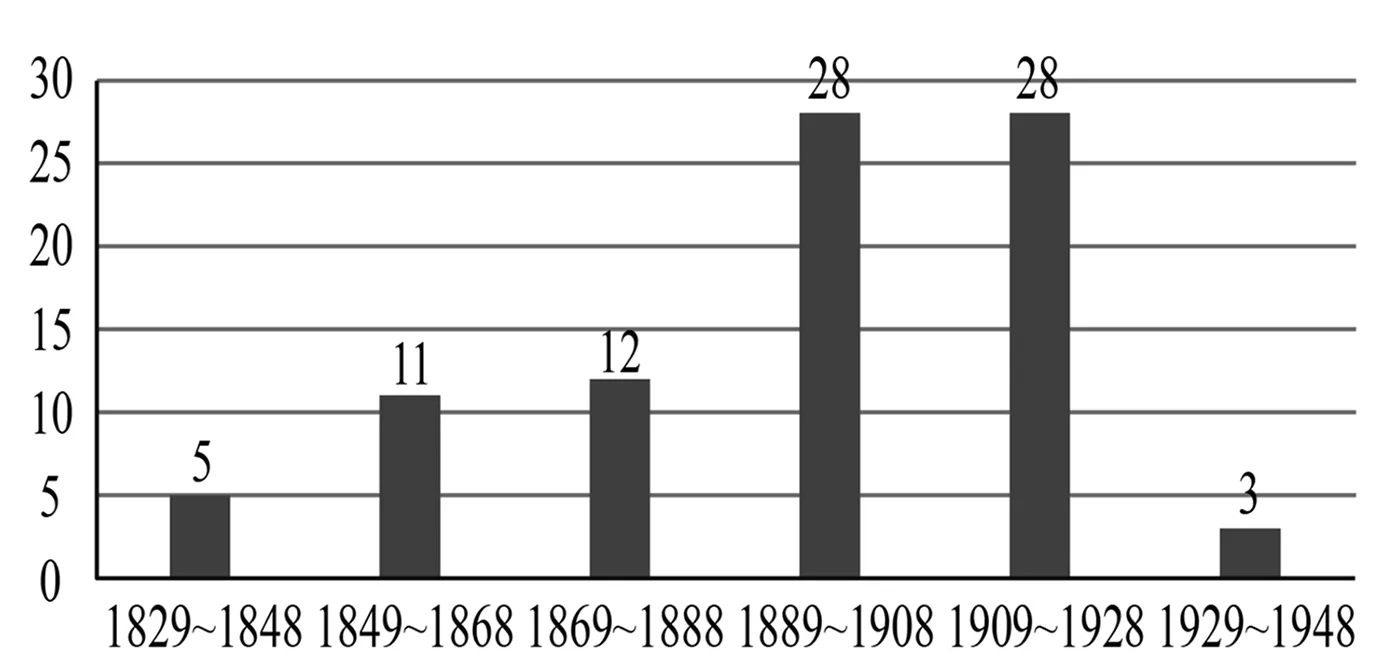
圖1 87種美英早期幾何教科書的出版時間分布
關于圓心角、圓周角和弦切角的內容主要位于“圓”“直線和圓”“角度測量”“圓和正多邊形”等章節中.其中,圓心角和圓周角的概念大多出現在“圓”一章的“定義”一節,圓心角定理大多出現在“圓心角”一節,而圓周角定理和弦切角定理大多出現在“角度測量”一節.
3 圓心角的概念
在58種給出圓心角概念的教科書中,定義方法可以分為鄰邊定義、靜態定義和頂點定義3類,具體分類情況見表1.

表1 圓心角概念的定義分類
4 圓心角定理
所謂圓心角定理,即在同圓或等圓中,相等的圓心角所對的弧相等,相等的弧所對的圓心角相等.因此,證明圓心角定理需證明以下兩個命題:
命題1 在同圓或等圓中,相等的圓心角所對的弧相等;
命題2 在同圓或等圓中,相等的弧所對的圓心角相等.
4.1 命題1的證明
·疊合法
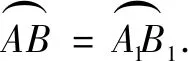

圖2 命題1的證明
·弧弦關系法
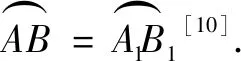
·比例法
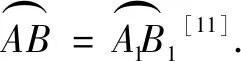
4.2 命題2的證明
·疊合法
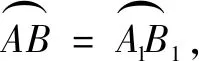
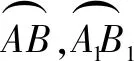
·弧弦關系法
·反證法
通過假設在同圓或等圓中,等弧所對圓心角不相等,再利用命題1中的結論即可導出矛盾.有3種教科書采用了這一方法.
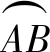
“幾年寫不出東西也屬正常,對待寫作要寬容,因為文字太強大了,人類一直想征服語言,但從來沒有成功過,文字和人一樣,有鼻子,有眼睛,有生命,有七情六欲,它們構成了一個多彩而充滿魔力的世界,在這個世界里,人獲得唯一真正的自由。所以那么多人喜歡文學,不過,人在駕馭文字的同時,文字也在反抗,所以,成功的畢竟是少數。成功也只是相對而言,即便是比爾蓋茨,也無法擁有全世界的財富。”一杭搖頭晃腦地說。
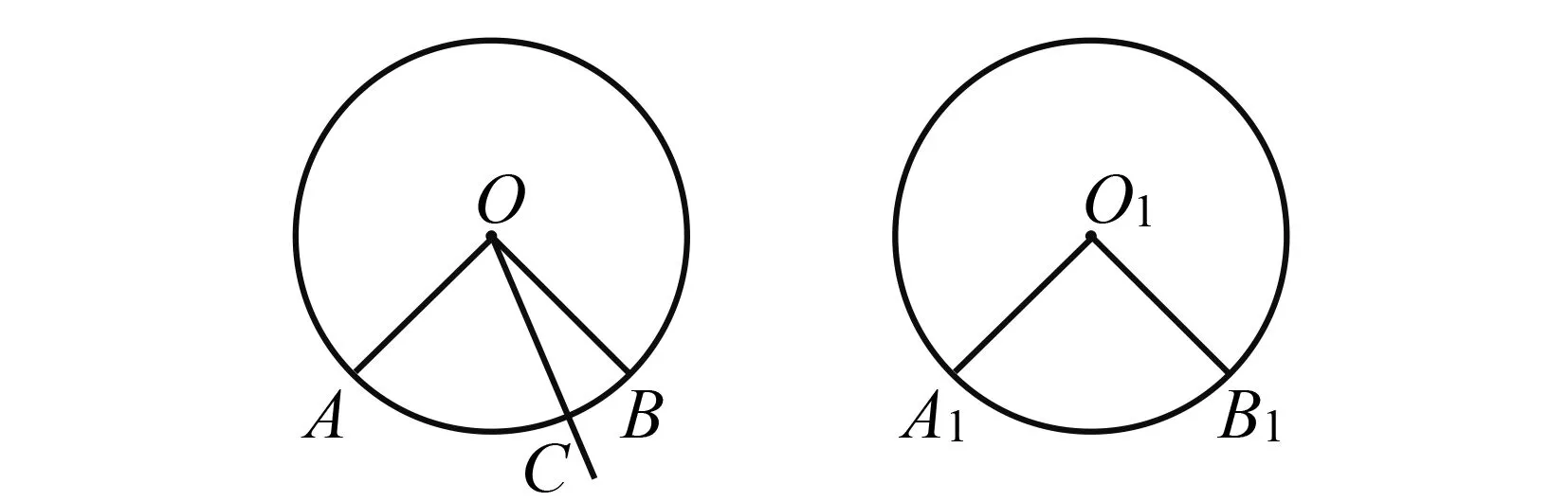
圖3 利用反證法證明命題2
·比例法
有2種教科書采用這一方法.在同圓或等圓中,因為圓心角所對的弧相等,即兩弧的比值為1,而圓心角的比值等于其所對弧長的比值,所以兩弧所對圓心角也相等[11].
·圓周角法
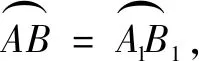
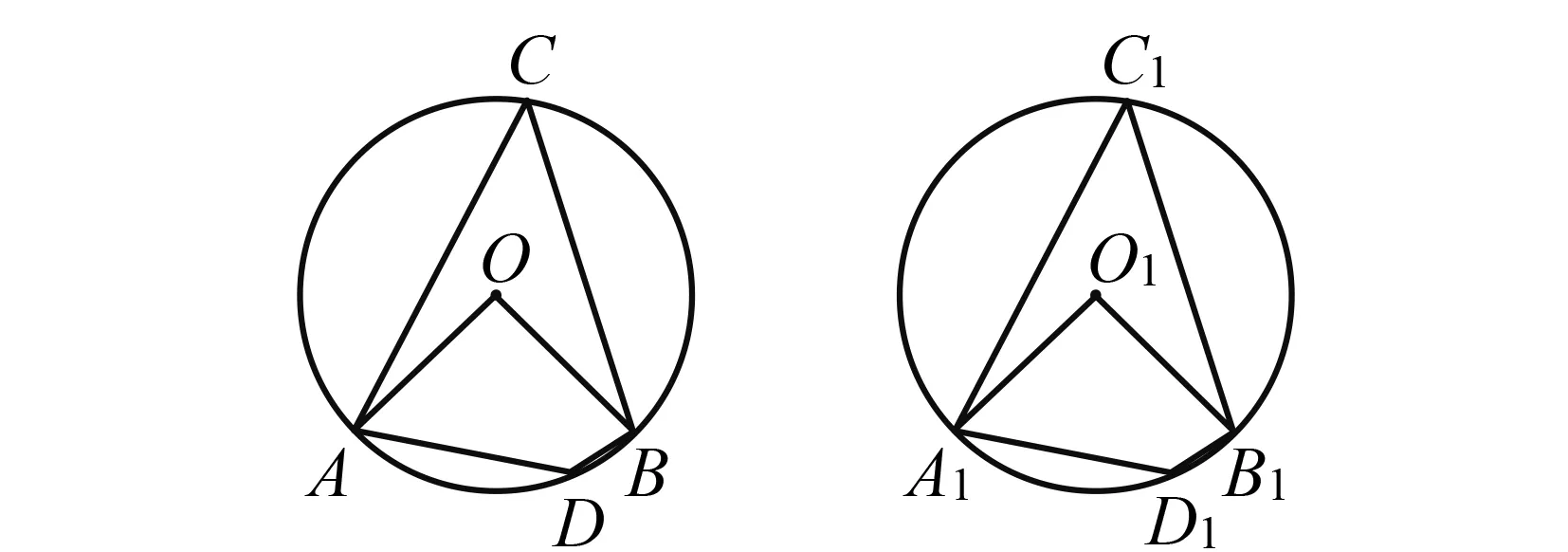
圖4 利用圓周角法證明命題2
·逆定律法
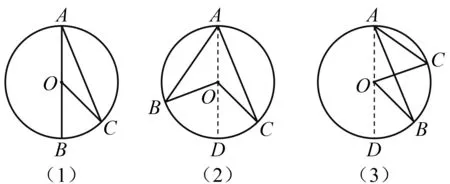
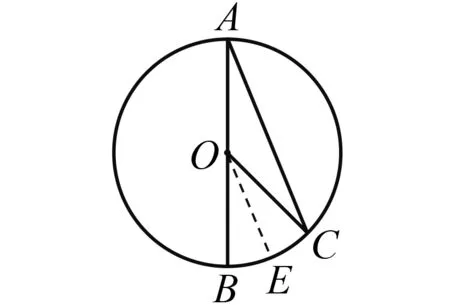
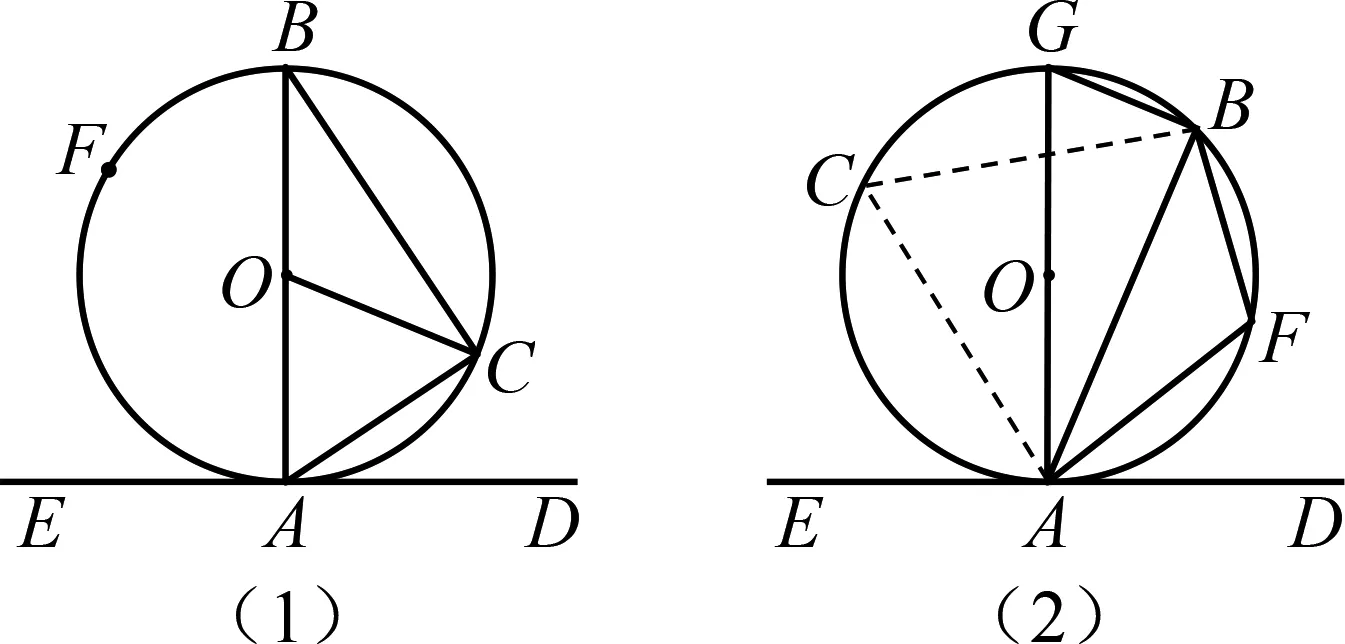
所謂逆定律(law of converse)是指:若A>B?X>Y,A=B?X=Y,A 在87種美英早期教科書中,除5種沒有給出圓周角概念外,其余82種教科書通常將圓周角稱為an inscribed angle或an angle inscribed in a circle,并給出了詳細解釋.圓周角概念的定義方法可以分為靜態定義、鄰邊定義和動態定義3類.表2是圓周角概念的定義分類情況. 表2 圓周角概念的定義分類 在87種美英早期教科書中,78種教科書將圓周角定理表述為:圓周角等于其所對弧的一半;9種教科書將其表述為:一條弧所對的圓周角等于這條弧所對圓心角的一半.后者與現行教科書給出的表述相一致.其中,證明上述定理的方法可以分為三角形外角法、平行線法以及弦切角法3類. 在給出圓周角定理證明過程的86種教科書中,有93%的教科書利用了三角形外角定理.如圖5,在⊙O上任取一個圓周角∠BAC,于是可以分三種情況進行討論,即圓心O在∠BAC的邊上、內部以及外部[17]. 圖5 利用三角形外角法證明圓周角定理 如圖5(1),即圓心O在∠BAC的邊AB上的情況.連結OC,因為OA=OC,所以∠BAC=∠C,于是,由三角形外角定理可知,∠BOC=∠BAC+∠C=2∠BAC.對于圖5(2)的情況,因為∠BOD=2∠BAD,∠DOC=2∠DAC,故∠BOC=2∠BAC.同理,對于圖5(3)的情況,也可得∠BOC=2∠BAC. 圖6 利用平行線法證明圓周角定理 有3種教科書采用了平行線法,即過圓心作圓心角一邊的平行線,進而完成證明.對于圓周角一邊過圓心的情形,如圖6,過圓心O作OE∥AC,于是∠BAC=∠BOE,∠C=∠COE.又因為OA=OC,所以∠BAC=∠C,于是∠BAC=∠BOE=∠COE,故∠BOC=2∠BAC.其他兩種情形的論證同6.1節[18]. 圖7 利用弦切角定理證明圓周角定理 另一種方法為Grund所采用.如圖7(2),因為∠BOA=2∠BAE,∠COA=2∠CAD,2(∠BAE+∠BAC+∠CAD)=360°,故得∠BOC=360°-(∠BOA+∠COA)=360°-2(∠BAE+∠CAD)=2∠BAC.[11] 在87種美英早期教科書中,并沒有直接給出弦切角的概念,而只是在弦切角定理中有所提及.其中,有54種教科書在定理或證明中將弦切角定義為由一條切線和一條過切點的弦所夾的角;有32種教科書將弦切角定義為由切線和弦所夾的角,但沒有指出弦切角的頂點在圓周上,而是在圖中指明弦切角;剩余1種教科書中沒有弦切角定理. 相比于弦切角概念的單一表述,弦切角定理的證明方法則非常豐富.所謂弦切角定理,即弦切角的大小等于它所夾的弧所對圓心角的一半,等于它所夾的弧所對的圓周角.在84種給出弦切角定理證明的教科書中,證明方法可以分為圓周角法、平行線法、垂徑定理法和動態法4類. 有超過半數的教科書在證明弦切角定理的時候,不約而同地用到了圓周角定理的3個推論,即 ①同弧或等弧所對的圓周角相等,②直徑所對的圓周角是直角,③圓內接四邊形的對角互補. 圖8 利用圓周角法證明弦切角定理 圖9 利用平行線法證明弦切角定理 圖10 利用垂徑定理法證明弦切角定理 圖11 利用動態法證明弦切角定理 綜上所述,在與圓有關的角這一主題上,美英早期教科書為我們呈現出圓心角、圓周角和弦切角的多種定義方式以及圓心角定理、圓周角定理和弦切角定理的多種證明方法,這些方式或方法為今日教學帶來了諸多啟示. 第一,在引入圓心角、圓周角和弦切角的概念時,可以先讓學生嘗試從這幾個角的名字出發進行描述,隨后向學生指出圓中這三個角的位置并讓學生予以補充,最后教師對不同的定義方法進行總結和完善.這樣循循善誘的教法,一方面給予了學生今后自學概念的方法,更重要的是讓學生體會知識的發生過程,有助于構建知識之諧. 第二,在證明圓心角定理、圓周角定理以及弦切角定理時,教科書上單一的證明方法可能會束縛學生的思維,形成思維定勢,這并不符合創新性人才培養的要求.教師可以引導學生一題多思、一題多解、一題多變,在掌握課本上的證明方法之后,開展小組探究活動,嘗試使用不同的工具來證明這些定理.一方面,“頭腦風暴”式的數學課堂有利于培養學生數學發現和創造能力,提高學生分析問題和解決問題的能力,最終開拓學生的思路,發展學生的智力.另一方面,學生在探究中能加深對于這幾個定理的理解,在豁然開朗時體會到成功所帶來的喜悅,有助于營造探究之樂. 第三,抽絲剝繭,深入挖掘定理證明背后的數學思想.例如,采用疊合法證明圓心角定理中的類比思想、利用三角形外角定理證明圓周角定理中的分類討論思想、采用平行線法證明弦切角定理中的化歸思想等,無疑是數學課堂上的寶貴思想養料.這一切不僅使原本枯燥的定理學習變得精彩紛呈,同時還有助于培養學生的數學抽象、邏輯推理、直觀想象等核心素養,有助于彰顯方法之美、實現能力之助. 第四,在介紹圓心角、圓周角和弦切角的概念及定理時,可以借助微視頻,展示各國數學家探索這三類角的概念和有關定理的過程,追溯知識源流,呈現多元文化.與此同時,數學家對于數學真理的不懈追求與熱愛,有助于激發學生學習數學的興趣,體會數學背后的理性精神,最終達成德育之效.5 圓周角的概念

6 圓周角定理
6.1 三角形外角法
6.2 平行線法
6.3 弦切角法

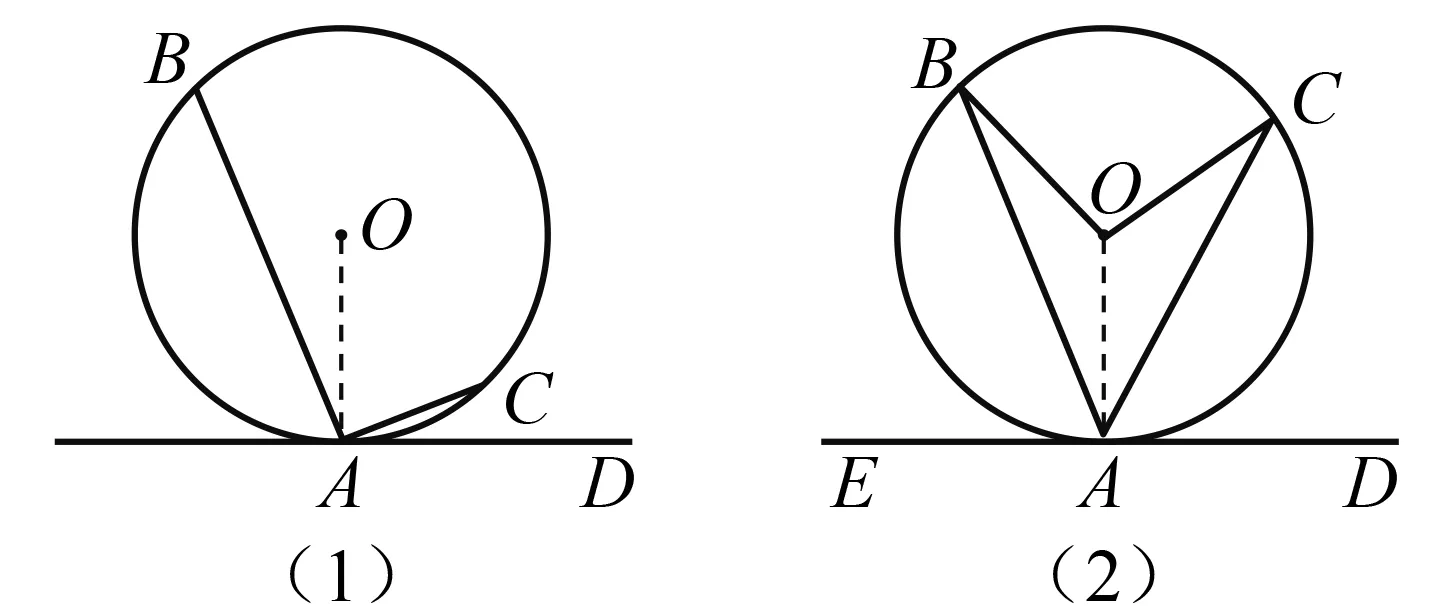
7 弦切角及弦切角定理
7.1 圓周角法
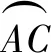
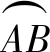
7.2 平行線法
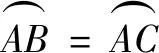
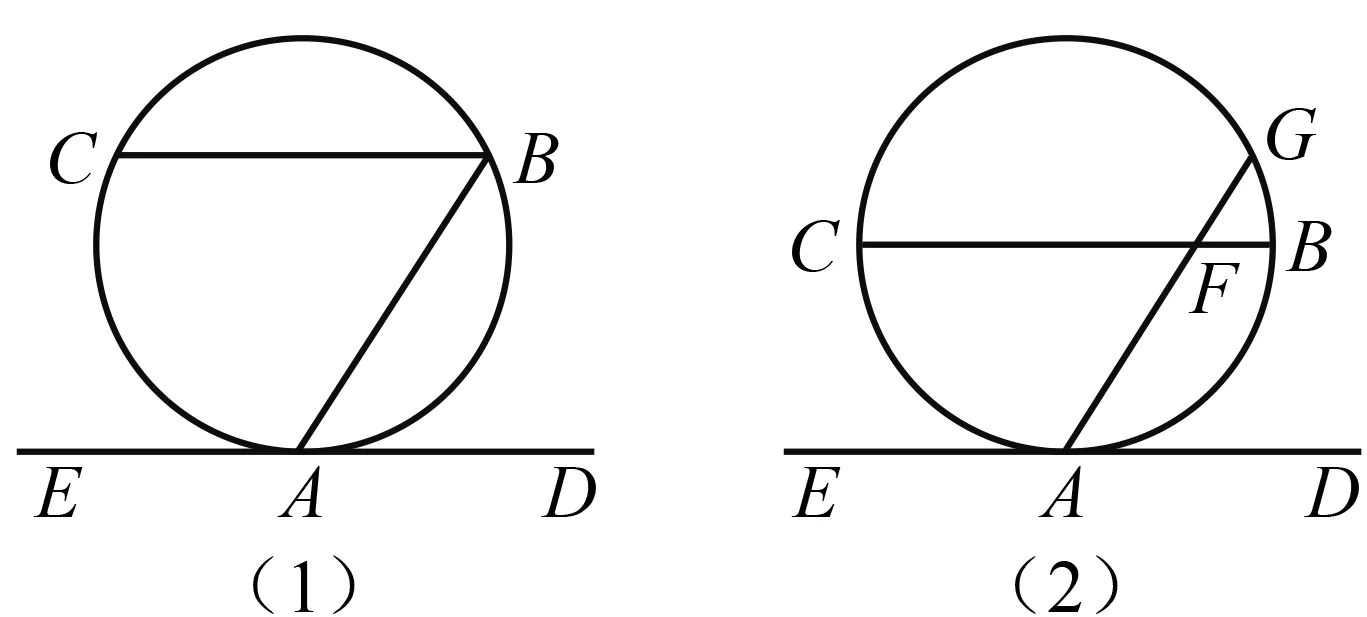

7.3 垂徑定理法

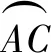
7.4 動態法

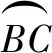
8 教學啟示

