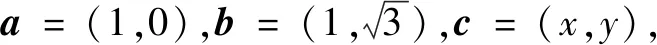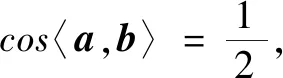談高三數學試卷講評策略
王文彬
(江蘇省太倉高級中學 215411)
高三數學試卷講評課是以“查漏補缺、優化策略、提升素養”為主要任務的.作為復習階段的基本課型,試卷講評課的主要教學目標是把握對應試卷的考試情況,合理彌補數學基礎知識的缺陷,突出重點難點,積累解題經驗,優化思維品質,提升關鍵能力.高三數學講評,要對解題過程中的思維過程(怎么想到的)進行充分剖析并展示給每一位學生,并在合理的“最近發展區”巧妙設計變式練習;同時要精準分析錯因,注重問題本質,優化解題方法.
1 學生層面1——關注學生參與
高三數學試卷講評課要關注學生的主動參與:一是引導學生關注自身進步,自主糾錯,自我評價,提升學好數學的自信心;二是引導學生自我反思,舉一反三;三是引導學生優化解法,深度思維,積累解題經驗.只有學生參與的高三數學試卷講評課,才是講效率、高品質的復習課[1].
高三數學試卷講評課中常見以下兩種具體操作模式:(1)正誤辨析式(展現錯誤—錯解辨析—解法糾錯—形成正解—變式練習—激勵評價),只有明確錯誤原因,才能有效改正,形成知識能力與習慣; (2)引申拓展式(展現解法—失誤分析—對比總結—問題變式—激勵評價—變式訓練),只有深入拓展引申,才能站上更高的平臺,一題多評,一題多得.無論應用哪種基本的講評操作模式,都離不開學生的親身參與與深入思考,只有學生深層次地參與其中,試卷講評才能發揮最好的效果.
2 學生層面2——注重錯因剖析
錯誤是試卷解答過程中不可避免的一種情況,高三數學試卷講評課要對基本失誤原因進行恰當歸因,這才是試卷講評中的一個重要環節.學生在考試過程中常出現過失性丟分、知識性失分或缺陷性錯誤,如審題不清、計算有錯、表達不規范、基礎知識掌握不牢或完全不會等.因此,在高三數學試卷講評課中,要通過示錯教學找到錯誤癥結,優化糾錯策略,及時查漏補缺,完善知識結構.
例1已知函數f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4個互異的實數根,則實數a的取值范圍為.
分析 通過方程的等價轉化,將一個方程轉化為兩個函數的問題,利用兩函數圖象的交點情況來研究對應方程根的問題,通過數形結合實現轉化.
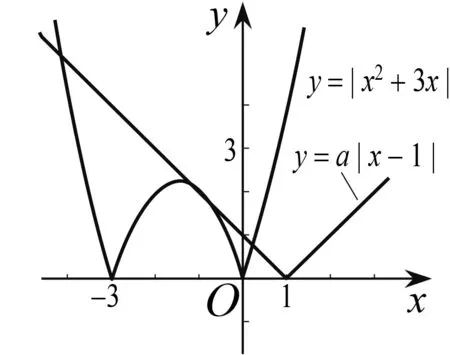
圖1
錯解 如圖1,在同一坐標系內作出函數y=f(x)與y=a|x-1|的圖象,當y=a|x-1|與y=f(x)的圖象相切時,由-ax+a= -x2-3x且a>0,整理得x2+(3-a)x+a=0,則Δ=(3-a)2-4a=a2-10a+9=0,解得a=1或a=9,故當y=a|x-1|與y=f(x)的圖象有四個交點時,1 錯解剖析 這里出現的錯誤就是利用“形”表示“數”時沒有實現恒等變形與轉化,轉化過程中出現偏差而導致錯誤. 解以上部分同錯解,解得a=1或a=9,故當y=a|x-1|與y=f(x)的圖象有四個交點時,0 高三數學試卷講評課一定要真正突出講評的重點以及試卷中相關試題的重點.一是講評對應試題的通技通法,強化審題訓練,展示思維過程,尋求試題解法的改進與優化,引領學生學會解題;二是講評出錯原因,分清錯誤類型,引導學生彌補解題過程中的錯誤或缺陷,夯實數學基礎知識與基本技能,完善數學認知結構與知識體系;三是講評數學試題的本質與內涵,通過問題變式,強化問題探究意識,發展學生的應變能力和創新意識;四是講評應試策略,規范解題過程,強化得分意識,讓學生“少丟分、多得分”. 分析 講評問題的基本點與重點,逐步推進,通過邏輯推理、數形結合以及數學運算來評析: (1)由解析幾何問題的文字敘述轉化為對應的圖形直觀(借助繪制草圖來實現數形結合);(2)建立對應的基本幾何量(用相關參數a,b,c以及對應的關系式來表示對應的線段長度和角的三角函數值);(3)借助平面幾何的輔助線構建,進一步確定對應線段MN的長度;(4)利用向量的線性關系式以及三角函數的定義來確定對應點A的坐標;(5)以相關點A的坐標滿足對應的雙曲線方程來構建關系式,解方程來確定離心率e的值. 圖2 高三數學試卷講評課要深入變式探究.只是停留在試卷分析與講評基礎上的高三數學試卷講評課,只能算是基本合格的課,只是停留在“門口”,入寶山而空手回.而合理的深入變式探究,發散數學思維,可從兩個方面展開:一是“一題多解”,拓寬解題思路,展現火熱的數學思考,尋求解法的改進與優化;二是“一題多變”,通過問題變式建構知識之間的內在聯系,在“變”的現象中發現“不變”的本質,在“不變”的本質中探索“變”的規律,強化問題探究意識,優化思維品質,培養應變能力和創新能力[2]. 例3在平面內,若有|a|=a·b=1,|b|=2,(c-a)·(2c-a-b)=0,則c·b的最大值為. 一題多解:3 教師層面1——突出講評重點
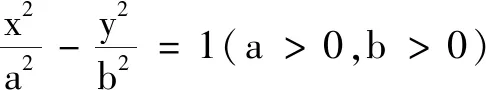

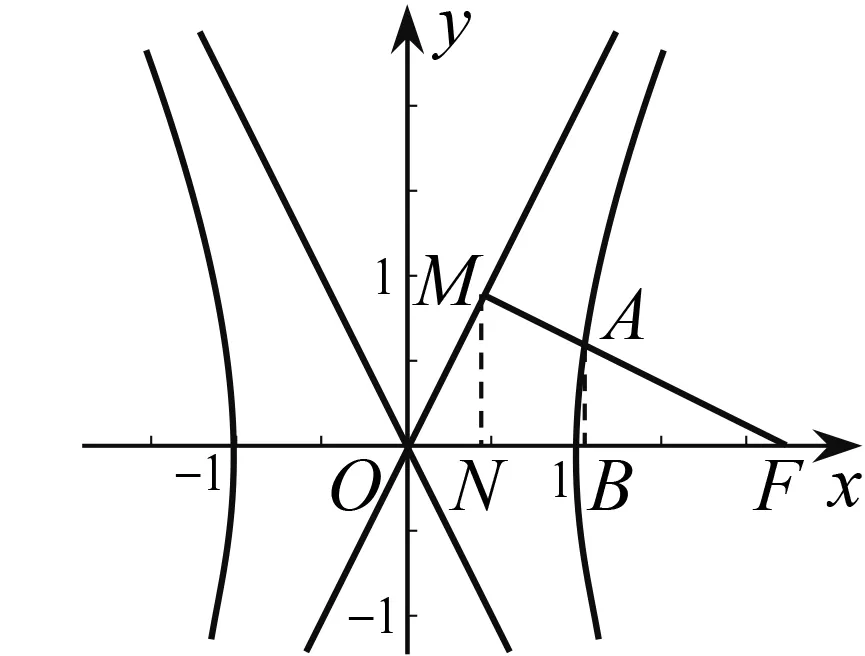
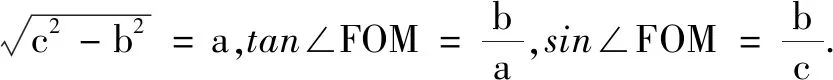
4 教師層面2——深入變式探究