鋰電池串并聯系統可靠性的建模與分析
朱海峰,劉學軍,丁 巍,程偉力
(施耐德電氣(中國)有限公司上海浦東分公司,上海 201203)
1 簡介
世界正處于碳達峰碳中和,構建清潔低碳,安全高效能源體系的大趨勢下,中國國家發展改革委,國家能源局也積極推動加快新型儲能發展的指導意見。以習近平新時代中國特色社會主義思想為指導,全面貫徹黨的十九大和十九屆二中、三中、四中、五中全會精神,落實“四個革命、一個合作”能源安全新戰略,以實現碳達峰碳中和為目標,將發展新型儲能作為提升能源電力系統調節能力、綜合效率和安全保障能力,支撐新型電力系統建設的重要舉措,以政策環境為有力保障,以市場機制為根本依托,以技術革新為內生動力,加快構建多輪驅動良好局面,推動儲能高質量發展。
新型儲能的能源形式越來越多樣化,其中包括氫能源,電化學能源,機械能源,蓄水能源,光伏能源等,電化學能源使用占比越來越高,鋰離子電池就是其中使用最為廣泛的電化學能源。
鋰電池使用過程中會根據終端產品負載情況,提供電壓和電流,保證其按照預期情況運行。在現有技術水平下,電池系統不可避免地需要將大量電池進行串并聯組合,以形成更高的電壓、更高容量的電池系統,來滿足終端應用的要求,如特斯拉model 3需要7 000多節圓柱型電芯進行串并聯,國家電網MWh級儲能電池系統需要萬節級以上電芯串并聯。
大量鋰離子電池的串并聯組合會導致儲能電池系統的可靠性降低,那么如何進行電池串并聯的設計就是儲能電池系統可靠性的關鍵一環。下面從電池串并聯的結構進行數學模型的建立,然后進行簡要分析,最后再從實際案例設計,給出單一因素的建議。
2 電池串并聯的數學模型建立與分析
2.1 電池的串并聯結構
串并聯結構模型分為串聯結構模型(如圖1)、并聯結構模型(如圖2),先并后串結構模型(圖3),先串后并結構模型(如圖4),混聯結構模型(如圖5和圖6)。這里需要解釋混聯結構模型,即超過一次串并聯結構的情況,如先并后串再并的結構模型,或者先串后并再串的結構模型。
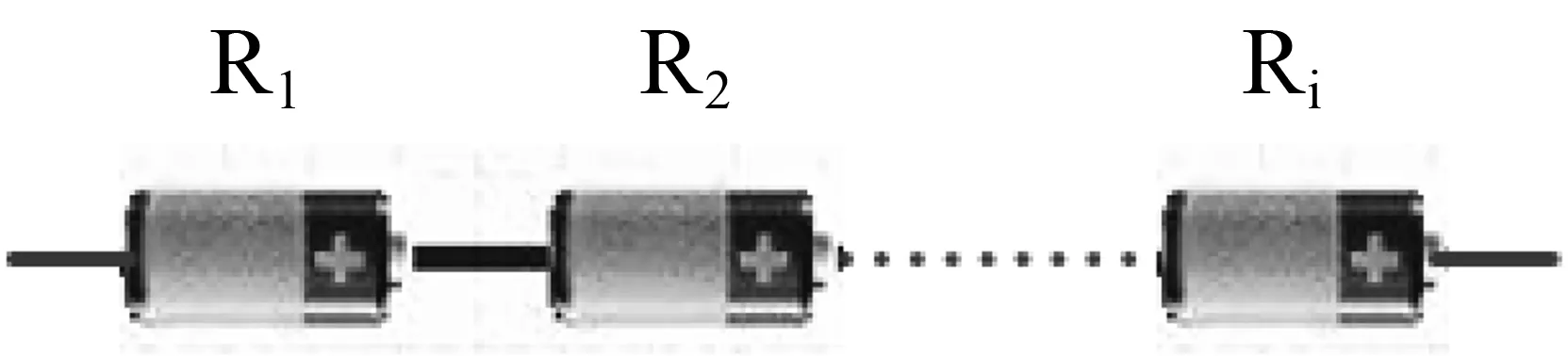
圖1 串聯結構模型Fig.1 Cell in series model.
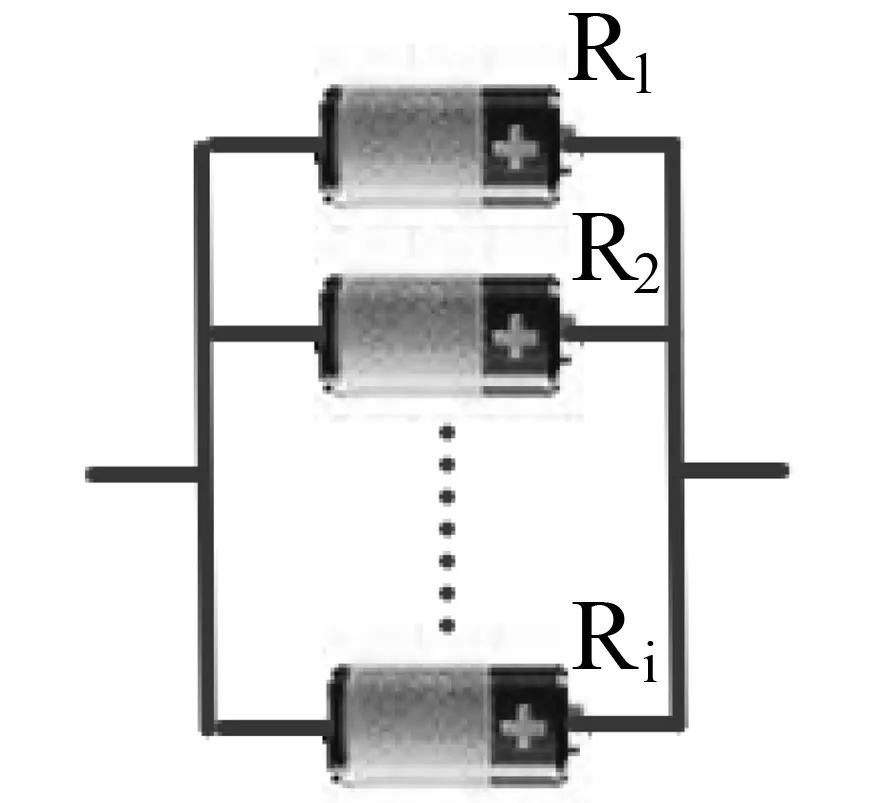
圖2 并聯結構模型Fig.2 Cell in parallel model.

圖3 先并聯后串聯結構模型Fig.3 Cell in parallel before series model.

圖4 先串聯后并聯結構模型Fig.4 Cell in series before parallel model.

圖5 混聯結構模型(先串聯后并聯再串聯)Fig.5 Hybrid Model (cell in series before parallel then series).
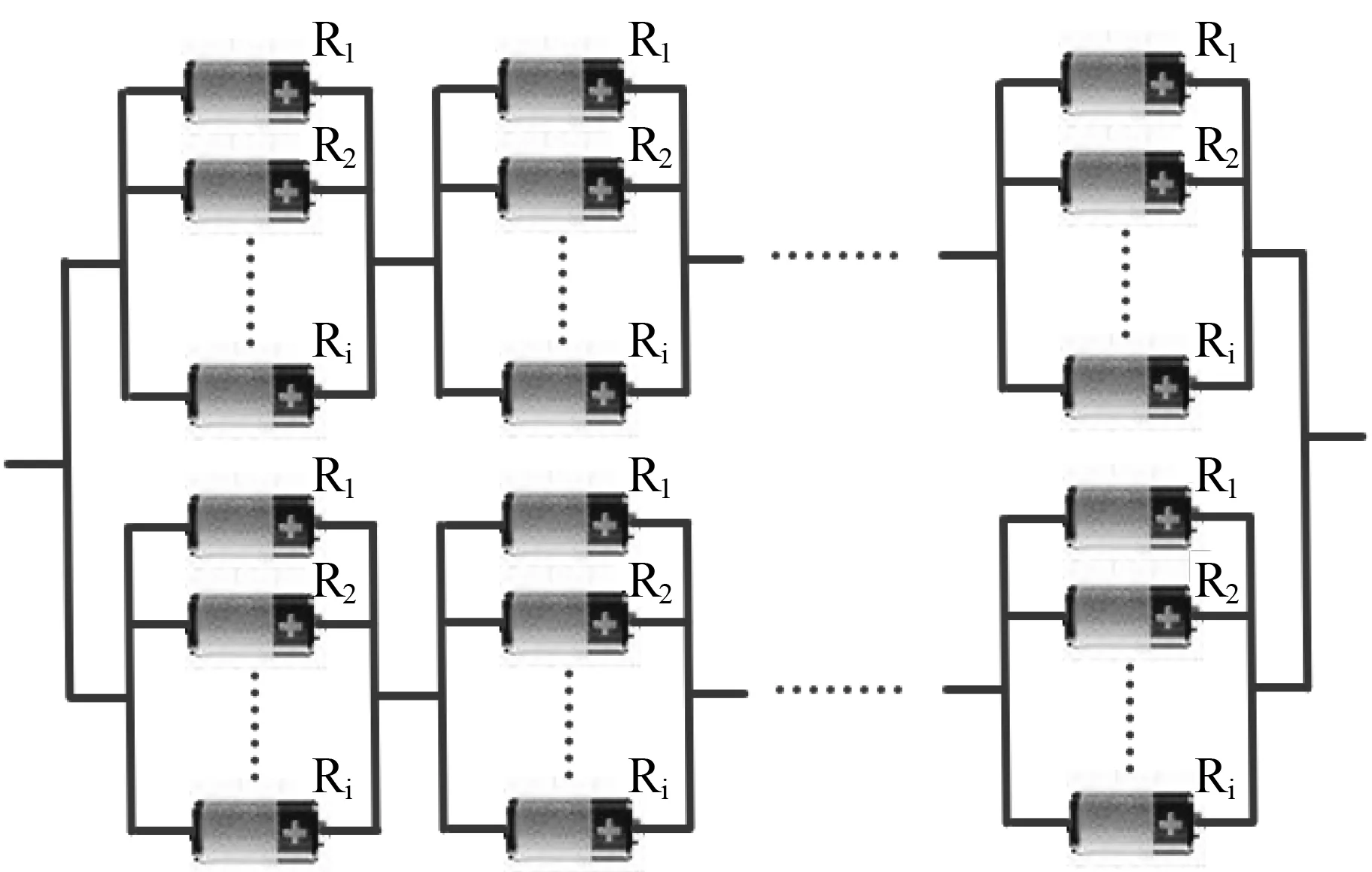
圖6 混聯結構模型(先并聯后串聯再并聯)Fig.6 Hybrid Model (cell in parallel before series then parallel).
2.2 串并聯結構模型的數學模型
假設模型中單體電池出現故障的概率是相同的,并且是相互獨立的,不考慮每個單元的復雜程度,環境的嚴酷程度以及工作時間長短等因素。
Rs(t)表示系統的可靠度,Ri=(1,2,3,……,n)表示第i個單元的可靠度,并且Ri均小于1。m表示并聯電池數,n表示串聯電池數。
2.2.1 串聯結構模型的數學模型
從圖1可以看出,串聯結構模型是屬于單一通道情況,需要每個串聯的單元都可靠,整個系統才可靠。所以可得串聯結構模型的數學模型為。
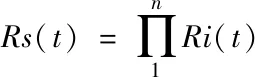
從串聯結構模型的數學模型可以看出,Rs(t)要小于每一個Ri(t)(n>1),即在串聯結構中,串聯單元越多,系統的可靠性越低。
2.2.2 并聯結構模型的數學模型
從圖2可以看出,并聯結構模型是多通道情況,單一單元可靠,整個系統就可靠。所以可得并聯結構模型的數學模型。

從并聯結構模型的數學模型可以看出,Rs(t)要大于每一個Ri(t)(m>1),即在并聯結構中,并聯單元越多,系統的可靠性越高。
2.2.3 先并聯后串聯結構模型的數學模型
從圖3可以看出,先并聯后串聯結構模型,是二級連接的結構,綜合并聯和串聯的數學模型。所以可得先并聯后串聯結構模型的數學模型。

從先并聯后串結構模型的數學模型可以看出,Rs(t)要小于每一個Ri(t)(n,m>1),即在先串聯后并聯結構中,串聯單元越少,并聯單元越多,系統的可靠性越高。
2.2.4 先串聯后并聯結構模型的數學模型
從圖4可以看出,先串聯后并聯結構模型是屬于二級連接的結構,綜合串聯和并聯的數學模型。所以可得先串聯后并聯結構模型的數學模型。

從串聯后并聯結構模型的數學模型可以看出,Rs(t)要小于每一個Ri(t),(n,m>1),即在先串聯后并聯結構中,串聯單元越少,并聯單元越多,系統的可靠性越高。
2.2.5 混聯結構模型的數學模型
從圖5可以看出,先串聯后并聯再串聯結構模型是屬于三級連接的結構,綜合串聯和并聯的數學模型。所以可得先串聯后并聯再串聯結構模型的數學模型。
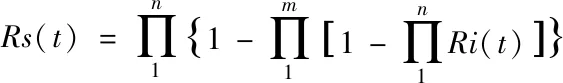
從圖6可以看出,先并聯后串聯再并聯結構模型是屬于三級連接的結構,綜合串聯和并聯的數學模型。所以可得先并聯后串聯再并聯結構模型的數學模型。

在混聯結構模型中,只描述了三級連接的結構。當然,按照模型可以擴展到多級連接結構模型,可以得到有著類似的數學模型。
2.3 儲能電池系統可靠性對比示例
一般儲能電池系統是由多個電池模塊組成的電池柜,電池柜也有可能串并聯使用。為了簡化可靠性對比,以常見電池模塊結構作為示例進行分析。
假設電池模塊由64節電芯組成,16節電芯串聯和4節電芯并聯結構。每節電芯可靠性是一致的。按照電池單體全生命周期順序0.999 997(6σ),0.997 3(3σ),0.954 5(2σ),0.9,0.8進行計算和比較。電池模塊按照四種常見的串并聯結構模型分別為4P16S,16S4P,(2P16S)2P,(2P8S)2P2S涵蓋二級連接的結構,三級連接的結構和四級連接的結構的主流設計。經計算可以得到表1。

表1 模組可靠性對比示例Table 1 Example of module reliability comparison.
以上數據表格使用0.999 996 6(6σ),0.997 3(3σ),0.954 5(2σ),0.9,0.8進行分析,是考慮產品全生命周期,電池的可靠性是隨著使用周期,逐步降低的。
從上面數據來看,在不同的電池可靠性數值下,以上四種串并聯結構模型的可靠性數值是有很大差異的。電池單體的可靠性越高,系統級別的可靠性越高,并且差異越小。電池單體的可靠性越低,即產品使用的生命周期后段,系統級別可靠性越差,并且差異越大。
3 結論
經過以上鋰電池系統使用的串聯結構的數學模型,并聯結構的數學模型,先并聯后串聯結構的數學模型,先串聯后并聯結構的數學模型以及混聯結構的數學模型的建立,然后建立實例進行可靠性的計算,從單一變量(電池連接結構差異)考慮和數學模型可以得到如下內容。
(1)針對二級連接方式的結構:
①優先選擇先并聯后串聯結構(先串聯后并聯結構組成的電池系統可靠性最好);
②先串聯后并聯結構組成的電池系統可靠性最差(先串聯會導致單路連接的結構可靠性變差)。
(2)三級以上的連接方式的結構:
①n×m級連接結構的可靠性未必比n×m+1級聯結結構的可靠性好,即多級連接的可靠性可以通過調整更小級別的模組結構進行優化;
②多級連接方式結構的數學模型的建立,可以根據單級連接結構進行推演,最終獲得多級連接結構可靠性的數學模型;
(3)只要鋰電池系統中電池的連接方式設計得當,復雜聯結結構系統的可靠性未必會比簡單聯結結構系統的可靠性低,甚至要高,可根據以上數學模型進行單一變量的推演,得到較優方案。

