基于動態阻抗匹配的單傳感器MPPT算法研究

蔣平，伍青，徐自強

(1.成都客車股份有限公司，四川成都，611731; 2.電子科技大學，四川成都，611731)

0 引言

由能源使用而帶來的環境污染問題日益嚴重，尋找新能源已經迫在眉睫。其中，太陽能以清潔，豐富獲得人們的青睞。但是，太陽能發電容易受到光照、溫度、負載等外界條件的影響，且轉化效率較低[1]。所以提高光伏電池的輸出功率，就可以在一定程度上優化光伏系統，增大經濟效益[2]。

現在比較常用的算法有開路電壓法和短路電流法[3]，該算法實現簡單，跟蹤速度也很快。但是該算法只能在特定的外界條件下使用，一旦環境出現變化該算法就會出現誤判，造成能源的浪費；擾動觀察法[4]是通過調整輸出電壓然后比較輸出功率來調整占空比的，控制方法相對簡單，但是穩定性較差；電導增量法[5]是通過計算光伏電池輸出功率對電壓求導的值來調整系統的輸出電壓，容易發生誤判。另外還有模糊控制[6]、變步長電導增量法[7]等新型的方法。這些方法在跟蹤速度和精度上都有很大的改進，但是大部分需要將光伏電池的輸出電壓和電流作為反饋量，而且控制方法較為復雜，使得一些算法的實用性較低。

為了使系統和算法更加簡單，跟蹤速度和精度更加完美。本文從減少反饋量入手，提出了一種基于動態阻抗匹配的單傳感器的簡單MPPT算法，最后在MATLAB/Simulink仿真平臺上驗證了其可行性。

1 光伏電池等效模型

光伏電池是由半導體構成的，可以吸收太陽能然后轉化為電能[8]。可以用一個電流源和一個二極管的并聯[9]來等效它的數學模型。其數學模型如圖1所示。

圖1 光伏電池等效模型

光伏電池的輸出方程為：

式中：Ipv是對外輸出電流；Io是二極管D的反向飽和電流；q是電子的電荷；K是波爾茲曼常數；A是D的理想因子；Tj是光伏電池的結溫；Upv是對外輸出電壓[10]。

對圖1的模型在一定的光照條件下進行SIMULINK仿真，得到圖2所示的光伏電池輸出U-P曲線。

圖2 U-P曲線

由圖2可以看出光伏電池的輸出功率有一個最大點。所以找到這個最大點便可以提高光伏系統的輸出功率。

2 基于動態阻抗匹配的單傳感器MPPT算法

■2.1 單傳感器MPPT的算法原理

根據戴維南定理，用一個電壓源E與一個內阻r的串聯來等效光伏陣列，當且僅當等效輸入負載R等于內阻r時[2]，電路輸出最大功率達到最大。由于內阻r是非線性的，將其定義為r=dUr/dIPV，Ur是內阻r上的電壓。光伏電池的輸出電壓UPV=E?Ur，從而可以推出r= ?dUPV/dIPV。

本文采用典型的BOOST電路來進行占空比調節，對于BOOST電路輸入電壓Upv與輸出電壓Uo之間的關 系 為UO=UPV/(1 ?D)。D為 占 空 比， 假 設BOOST電路損耗為零，根據能量守恒可以推出等效輸入負載R=UPV/IPV= ( 1 ?D)2RL,即可以推出光伏電池的輸出電壓Upv如公式(3)。

將占空比D看成電流Ipv的函數，公式兩邊同時對電流Ipv求導并整理，可得如下公式：

由圖2可以看出光伏電池的輸出功率有且只有一個最大點，所以公式(5)中一定存在一點使得內阻r與等效阻抗R相等，而該點就是最大功率點。所以可以由公式(5)得出在最大功率點時滿足dD/dIPV= ( 1 ?D) /IPV。

(1)當dD/dIPV< ( 1 ?D) /IPV時，推出內阻r小于等效電阻R，這時就增加占空比減小等效電阻R。

(2)當dD/dIPV> ( 1 ?D) /IPV時，推出內阻r大于等效電阻R，這時就減小占空比增加等效電阻R。

所以該算法通過實時采樣光伏電流Ipv，然后通過不斷調整BOOST電路的占空比來實現光伏電池的內阻r與等效電阻R相等，從而實現光伏電池的最大功率追蹤。

■2.2 基于二分法的MPPT算法實現

采用二分法同時調節占空比和步長的大小，可以提高系統的追蹤速度和穩定精度。整個算法的具體步驟如下：

(1)先初始化占空比d0和步長a0，以及對輸出電流IPV進行采樣。先判斷環境是否發生突變，如果環境發生突變了就重新初始化占空比d0和步長a0，否則就進行步驟2的運算。

(2)判斷dIPV是否為零，如果dIPV等于零則占空比dk+1不做變化，步長ak+1等于零；如果dIPV不等于零，則進行步驟3的運算。

(3)判斷dD/dIPV與 (1 ?D) /IPV是否相等，如果相等則占空比不做任何改變，如果不相等就進一步判斷連續兩次的步長是否同號。如果ak與ak-1異號，則說明步長已經跨過最大點功率所對應的步長，就取dk+1=(dk+dk-1)/2,為了減少波動步長也采用二分法即取ak+1=-ak/2。如果ak與ak-1同號就進行步驟4的運算。

(4)比 較dD/dIPV與與(1 ?D) /IPV的 大 小， 如 果dD/dIPV< ( 1 ?D) /IPV則 加大占空比，反之就減小占空比。

(5)重復以上步驟。

具體控制流程如圖3所示。圖3中d0為初始占空比，a0為初始占空比變化步長。

圖3 新型MPPT流程圖

3 仿真結果與分析

在MATLAB/Simulink仿真平臺上，搭建基于BOOST電路的光伏系統仿真模型，如圖4所示。

圖4 光伏系統仿真模型

圖4中設定仿真參數為：電路為Boost直流電路，電感值L為360μH，C1、C2均為1000μF；光伏電池的短路電流為7A，開路電壓24V，UPmax為20 16V，IPmax為6 3A。設立仿真條件為：0s時太陽光強度由0W/m2突變為1000 W/m2；0 2s時太陽光照強度由1000 W/m2突變為700 W/m2；0 3s時太陽光照強度由700 W/m2突變為1000 W/m2；0 4s時負載由20Ω突變為6 67Ω。在該仿真條件下對比了定步長d=0 01的電導增量法、新的不對稱變步長的電導增量法以及基于動態阻抗匹配的單傳感器MPPT算法。

對不同的算法進行仿真，得到的光伏組件輸出功率的仿真結果如圖5~圖7所示。

圖5 d=0 01的定步長電導增量法

圖7 基于動態阻抗匹配的單傳感器MPPT算法

從圖5和圖7中可以看出，定步長電導增量法和新型MPPT算法在負載發生變化時都能重新追蹤到最大功率點，但是后者在最大功率的波動明顯小于前者；對比圖6與圖7，不對稱變步長電導增量法與新型MPPT算法在最大功率點的波動較小，但是當負載發生變化時，不對稱變步長電導增量法不能重新跟蹤到最大功率點。

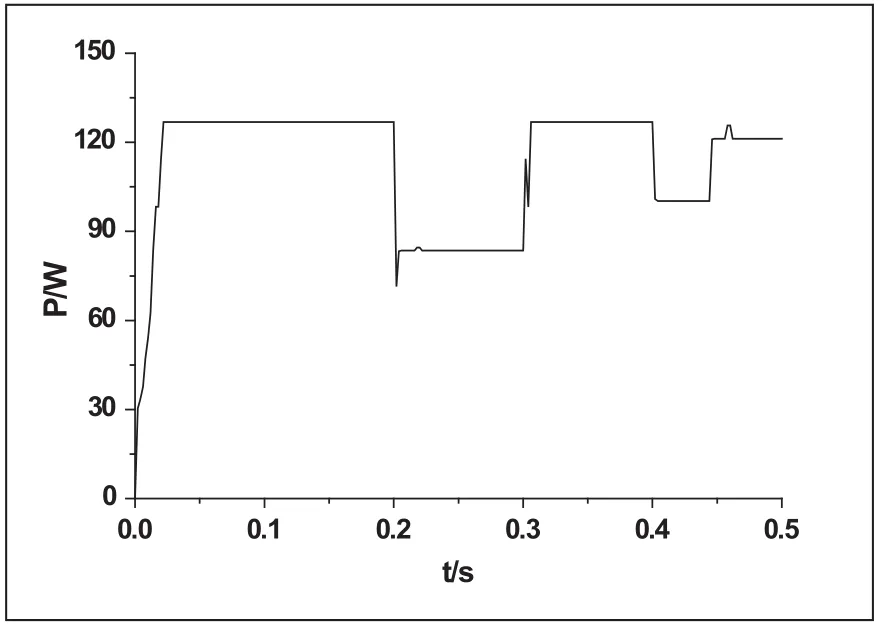
圖6 不對稱變步長電導增量法

為了更清楚的對比新型算法的優點，將具體的仿真結果數據制成表1。其中t代表仿真環境變化時跟蹤到MPP點的時間；Pmax代表環境穩定時的最大功率。從表1的仿真數據可知，當光照強度或者負載發生變化時新型MPPT算法的追蹤速度可以達到8ms遠遠快于另外兩種算法。而且新型MPPT算法不論在哪種仿真環境下所追蹤到的最大功率都比相同環境下的定步長電導增量法和不對稱變步長電導增量法大，所以新型MPPT算法的效率更高。從流程圖3還可以看出，新型MPPT算法的占空比和步長都利用二分法來不斷進行調整。不僅控制方法簡單，對不同光伏系統的適用性也較強。

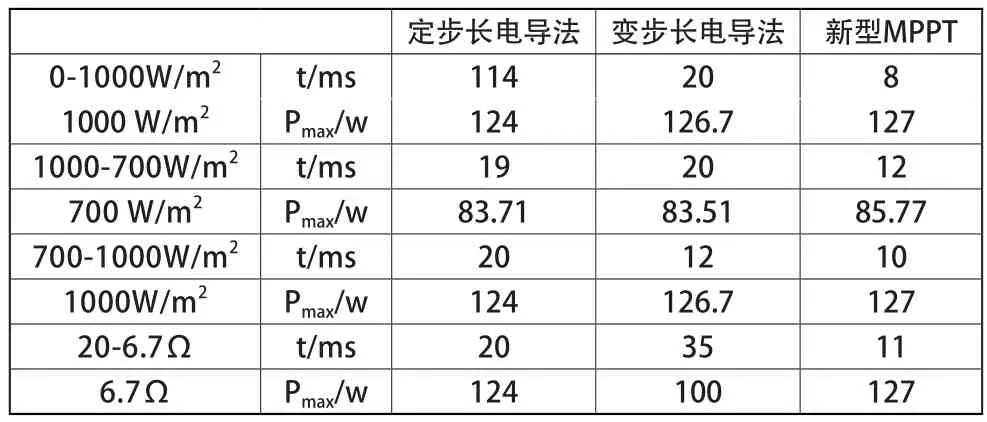
表1 仿真結果數據

4 總結

本文提出了基于動態阻抗匹配的單傳感器MPPT算法，與傳統的定步長電導增量法和新型的不對稱變步長電導增量法進行對比，該算法具有如下優勢：

（1）基于動態阻抗匹配的單傳感器MPPT算法只需要將輸出電流作為反饋量，可以減少由電壓反饋帶來的檢測誤差，提高系統精度。尤其是在硬件方面可以減少電壓傳感器的使用，即節約硬件成本又減少硬件體積。

（2）基于動態阻抗匹配的單傳感器MPPT算法采用二分法同時來改變占空比和步長，二分法來改變占空比可以提高系統的動態性能，快速的追蹤到MPP。二分法用于步長的改變，理論上可以無限減少穩態誤差，減少再MPP點的波動。算法簡單，對不同光伏系統的適用性較強。

（3）基于動態阻抗匹配的單傳感器MPPT算法在跟蹤速度和在最大功率點的穩定性上都優于傳統算法，尤其是在負載突變時也能較快并準確的跟蹤到最大點。