載頻-重頻聯合捷變雷達目標參數估計方法

劉智星, 全英匯,*, 沙明輝, 方 文, 高 霞, 邢孟道

(1. 西安電子科技大學電子工程學院, 陜西 西安 710071; 2. 北京無線電測量研究所, 北京 100854;3. 西安電子科技大學前沿交叉研究院, 陜西 西安 710071)

0 引 言

載頻-重頻聯合捷變雷達由于其脈沖間參數隨機捷變的特性,較傳統參數固定雷達更加難以被偵察干擾機截獲與識別,在低截獲、抗干擾等方面有著優越的性能[1-9]。但是由于脈間載頻和重頻的隨機變化,在對載頻-重頻捷變雷達進行相參積累時,回波信號的相位完全沒有線性特性,導致傳統基于快速傅里葉變換(fast Fourier transform,FFT)的相參積累技術無法直接應用,最終影響了目標檢測與參數估計。

捷變體制雷達以其優異的低截獲和抗干擾性能,受到了國內外眾多專家學者的廣泛關注,并取得了一些成果。對于載頻捷變雷達,壓縮感知理論可有效解決頻率捷變所帶來的回波信號相參積累難題[10-13],在稀疏約束的條件下,利用發射信號的載頻捷變序列,構造與目標參數信息相關的字典矩陣,從而實現對目標參數的估計。此外,文獻[14]將稀疏貝葉斯學習的方法應用到捷變頻雷達目標稀疏重構中,實現對目標信息的精確重構,并有效抑制了旁瓣。針對高速運動目標,文獻[15]提出了一種捷變頻雷達相參積累方法,該方法首先采用楔石形變換校正目標運動所引起的距離徙動,然后再利用拉東變換補償多普勒頻率模糊,并采用chirp-z變換實現回波的相干積分,最后通過逆傅里葉變換完成相參積累。對于載頻捷變所引起的回波相位的變化,文獻[16]采用最小波形熵準則作為代價函數進行相位補償,再通過FFT完成回波信號的相參積累。

對于重頻捷變雷達,劉振等采用了基于壓縮感知理論的重頻捷變雷達信號處理方法[17-19],將隨機重頻捷變信號的速度估計問題抽象為一個典型的壓縮感知模型,完成了回波信號的相參積累,且具有較高的速度分辨率。重頻捷變雷達回波在同一距離單元上不同脈沖間采樣具有非均勻特性。因此,對于重頻捷變雷達的相參積累問題可利用自適應迭代算法[20],該算法具有較小的頻譜泄漏、無多普勒模糊的優點,提升了雷達的目標檢測性能。此外,還可直接利用非均勻傅里葉變換完成回波信號的相參積累[21]。文獻[22]提出了一種基于拉東-非均勻分數階傅里葉變換的重頻捷變雷達相參積累方法,該方法通過在構造的運動參數空間中搜索來校正距離單元徙動,并利用非均勻分數階傅里葉變換對多普勒頻率進行補償,且在低信噪比下也能獲得良好的檢測性能。文獻[23]提出了一種基于拉東-非均勻快速傅里葉變換的方法,解決了由于方位向上非均勻采樣所帶來的相參積累難題。對于載頻-重頻聯合捷變雷達,利用數理統計方法,文獻[24]分析了載頻-重頻聯合捷變信號的平均模糊函數,得到了其隨機捷變參數與分辨能力、副瓣抑制能力及解模糊能力之間的數值關系,為波形的優化設計提供了理論支撐。在壓縮感知理論框架下,文獻[25]采用正交匹配追蹤算法完成了載頻-重頻聯合捷變雷達回波信號的相參積累,并通過實測數據驗證了該算法的有效性。

可以看出,國內外學者相關的研究主要聚焦于載頻捷變或重頻捷變,而對載頻-重頻聯合捷變的相關研究較少。因此,本文主要針對載頻-重頻聯合捷變體制雷達,開展雷達目標參數估計研究。

本文提出了一種基于多重信號分類(multiple signal classification,MUSIC)算法的載頻-重頻聯合捷變雷達目標參數估計方法,旨在解決載頻-重頻聯合捷變所帶來的目標參數估計難題,將時域信號處理等效成空域信號處理,并利用陣列信號處理中的超分辨信號處理方法完成了目標距離和速度的聯合估計,實現了距離和速度的超分辨。實驗證明,與傳統時域相關算法相比,本文所提方法具有較高的分辨率。

1 載頻-重頻聯合捷變雷達信號模型

載頻-重頻聯合捷變雷達發射信號模型如圖1所示,假設在一個相干處理間隔(coherent processing interval,CPI)內雷達共發射M個脈沖,脈內調制為線性調頻,第m個脈沖的載頻為fm,對應的慢時間為tm,則載頻-重頻聯合捷變雷達信號模型可以表示為

(1)

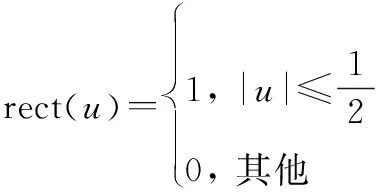
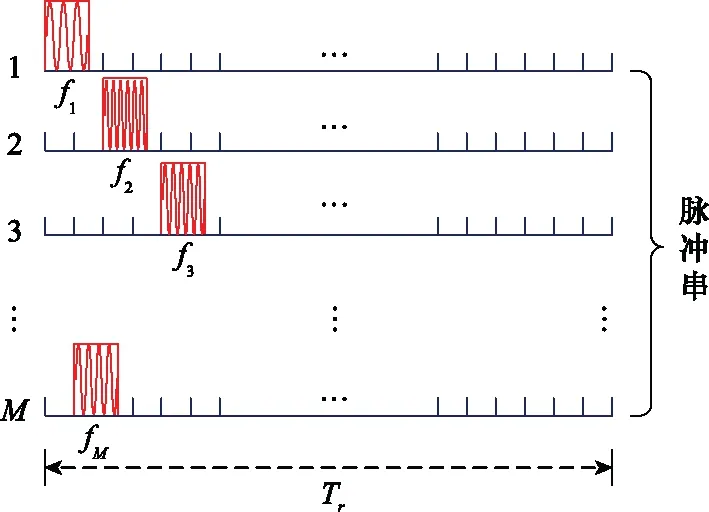
圖1 載頻-重頻聯合捷變雷達信號模型Fig.1 Signal model of frequency agility and pulse repetition frequency agility radar

2 載頻-重頻聯合捷變雷達信號處理

與傳統的參數固定雷達不同,載頻-重頻聯合捷變雷達的回波信號經過脈沖壓縮處理后,由于隨機性的引入,回波的距離相位項與速度相位項隨著載頻和重頻的變化而變化。利用FFT的方法已無法完成回波信號的相參積累,因此針對載頻-重頻聯合隨機捷變所帶來的雷達參數估計問題,本文利用陣列信號的處理方法來完成目標距離和速度的超分辨估計,將雷達時域信號處理等效為空域陣列信號處理,即目標的距離和速度信息的估計轉化為陣列信號處理中二維參數的估計問題。

2.1 雷達回波建模

假設在觀測場景中存在G個Swerlling I型運動目標,第g個目標的徑向距離為rg,徑向速度為vg(假設朝向雷達運動的目標速度為正),則經過目標反射,雷達回波信號可以表示為

(2)

式中:τg表示雷達發射信號與接收信號的時延;n(t,tm)表示服從高斯分布的噪聲。則雷達回波信號經過與對應載頻fm混頻和脈沖壓縮后可以表示為

exp(-j2πfmτg)+n(t,tm)

(3)

式中:sinc(·)表示辛格函數;Ag表示第g個目標脈壓的幅值,將τg=2(rg-vgtm)/c(c為光速)代入式(3)可得

(4)

將載頻fm=f0+a(m)Δf和慢時間tm=(m-1)Tr+b(m)ΔT代入式(4)可得

(5)

從式(5)可以看出,載頻-重頻聯合捷變雷達的相位的變化與引入的隨機變量a(m)和b(m)有關,這導致回波相位完全沒有線性特性,此時FFT算法會完全失效,從而影響目標參數的提取。

2.2 雷達參數估計

2.2.1 模型空時等效

為了便于分析,式(5)可改寫為

(6)

式中:

式(6)表示雷達接收的單個脈沖信號,為了便于后續的信號處理以及模型空時等效,將雷達在一個CPI內接收到的回波數據按行重排為數據矩陣形式,則回波數據矩陣可表示為

(7)

式中:⊙表示哈達瑪積；

Sr(t)=[Sr(t,1),Sr(t,2),…,Sr(t,M)]T

a(rg)=[φrg(1),φrg(2),…,φrg(M)]T

a(vg)=[φvg(1),φvg(2),…,φvg(M)]T

n(t)=[n1(t),n2(t),…,nM(t)]T

令a(rg,vg)=a(rg)⊙a(vg),其包含了目標的距離和速度信息,則式(7)可進一步改寫為

(8)

由式(8)可以看出,雷達在一個CPI內接收到的回波數據經過下變頻和脈沖壓縮處理得到的矩陣Sr(t)可以等效為陣元數為M的陣列的多次同步采樣,距離向上的一次采樣類似于陣列的一次快拍采樣數據,矢量a(rg,vg)相當于陣列的導向矢量,對目標距離和速度的估計可視為陣列信號處理中二維參數估計問題。

2.2.2 距離速度聯合超分辨估計

由第2.2.1節分析,目標的距離和速度可利用陣列信號中的信號子空間類處理方法進行超分辨估計。本文采用MUSIC算法對目標的距離和速度進行估計,該算法的基本思想是對任意陣列輸出數據的協方差矩陣進行特征分解,獲取信號子空間和噪聲子空間,利用信號子空間與噪聲子空間的正交性,構建空間譜函數,通過譜峰搜索來估計信號的參數。

MUSIC算法作為一種超分辨估計算法,在信號子空間和噪聲子空間獲取時,需要預先確定信號源數量,即觀測場景中的目標個數。本文采用基于最小描述長度(minimum description length,MDL)準則[26]的方法來估計觀測場景中的目標個數,首先計算式(8)所示的回波數據矩陣的協方差矩陣為

RSr=E[Sr(Sr)H]

(9)

式中:E[·]表示求期望;(·)H表示矩陣的共軛轉置。接下來對回波數據矩陣的協方差矩陣RSr進行特征值分解：

(10)

式中:USr=[u1,u2,…,uM]表示特征向量矩陣；ΛSr是由協方差矩陣的特征值構成的對角陣。

假設觀測場景中有G個目標,則基于MDL準則的目標個數估計方法需最小化如下的對數似然函數:

(11)

式中:λi表示RSr的特征值;M表示陣元數,即一個CPI內的脈沖數;N表示快拍數,即距離向上的采樣點數,根據式(11)可得基于MDL準則的目標數目判定方法:

(12)

由式(12)即可估計出目標的個數G,則式(10)可改寫為

(13)

式中:Us為G個大特征值對應的特征向量張成的子空間,即信號子空間;Un為(M-G)個小特征值對應的特征向量張成的子空間,即噪聲子空間;Λs表示G個大特征值構成的對角矩陣;Λn表示其余的小特征值構成的對角矩陣。根據MUSIC算法,構建如下空間譜函數:

(14)

根據信號子空間與噪聲子空間的正交性,譜函數P(r,v)在距離r和速度v處會形成譜峰。因此,通過搜索P(r,v)的譜峰值就可獲得目標的距離和速度信息。

3 實驗結果與分析

3.1 仿真數據分析

為驗證基于MUSIC算法的載頻-重頻聯合捷變雷達目標參數估計方法的有效性,采用Matlab軟件進行仿真實驗,雷達工作在Ku波段,脈內波形調制為線性調頻信號,具體仿真參數如表1所示。

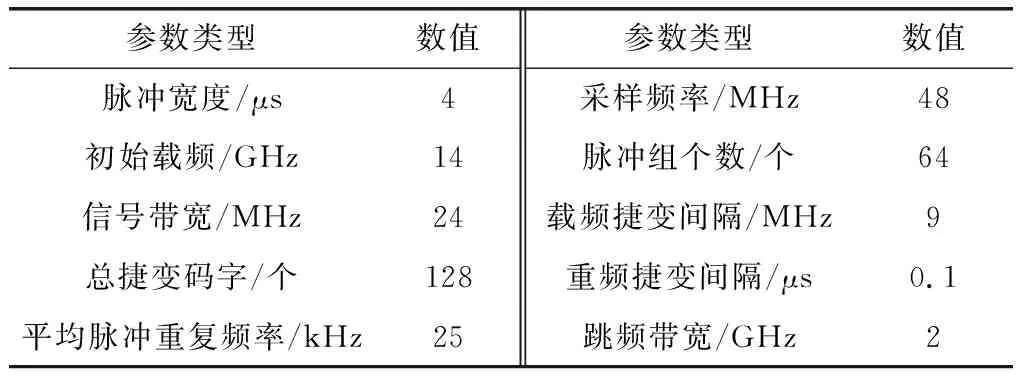
表1 仿真參數

如圖2和圖3所示,根據隨機捷變碼字序列,分別選取64個脈沖的載頻和重頻,假定觀測場景中存在兩個目標:目標1的距離和速度為[4 002.6 m,41.8 m/s],目標2的距離和速度為[4 003.9 m,83.7 m/s],信噪比均為5 dB,雷達回波經過下變頻和脈壓后結果如圖4所示,圖4中只出現了一個峰值,這是由于目標1和目標2距離太近,即兩個目標在同一個距離分辨單元,從而導致脈沖壓縮處理和傳統的雷達無法分辨出兩個目標。

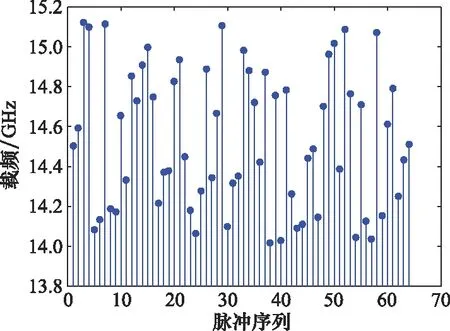
圖2 載頻捷變序列Fig.2 Carrier frequency agility sequence

圖3 重頻捷變序列Fig.3 Pulse repetition frequency agility sequence

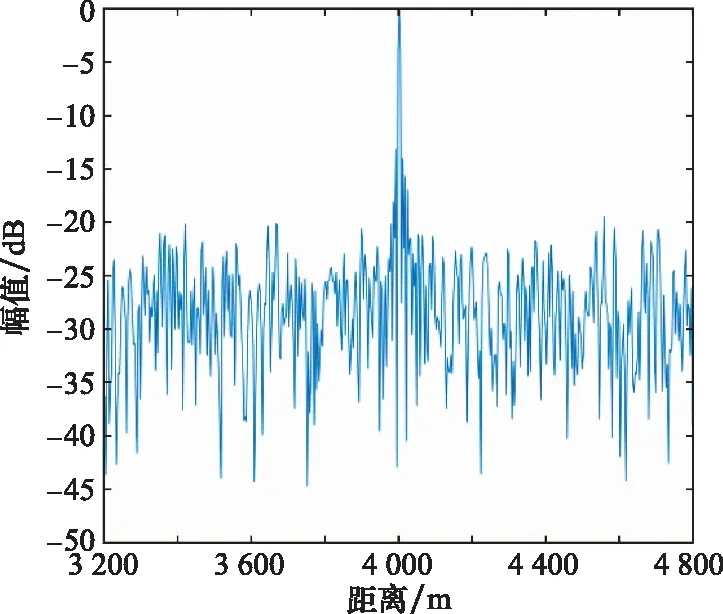
圖4 單個脈沖脈壓結果圖Fig.4 Result of single pulse compression

下面根據發射信號的載頻和重頻捷變序列,構造矢量a(rg,vg),并采用MUSIC算法對脈壓后的回波數據進行處理,目標參數估計結果如圖5所示。從圖5可以看出,本文所采用的方法在距離向上可分辨位于同一距離分辨單元的目標,目標1的估計值為[4 002.604 m,41.852 m/s],目標2的估計值為[4 003.906 m,83.705 m/s],兩個目標的距離和速度的估計誤差可忽略不計,仿真結果進一步驗證了本文所提基于MUSIC算法的載頻-重頻聯合捷變雷達目標參數估計方法的有效性。

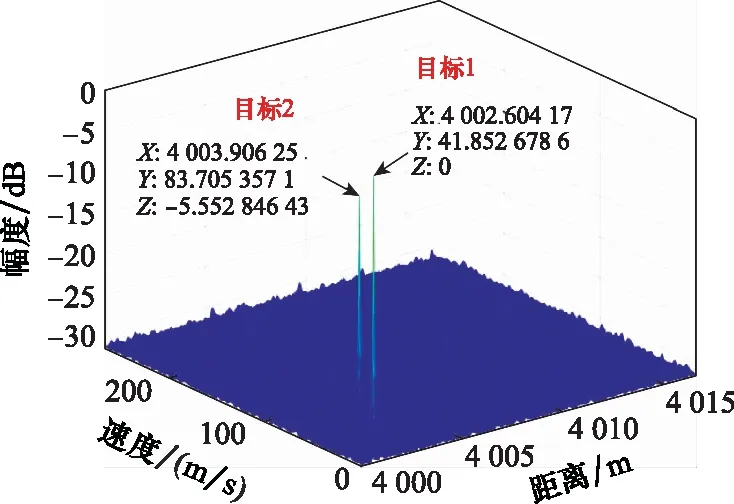
圖5 目標參數估計結果Fig.5 Result of target parameter estimation

圖6和圖7分別給出了本文所提的目標參數估計方法與時域相關算法在距離分辨率和速度分辨率方面的比較,目標的距離和速度分別為[4 002.6 m,41.8 m/s]。本文將陣列信號處理中的超分辨處理方法應用到目標的參數估計中,從仿真結果可以看出,本文提出的參數估計方法的距離分辨率和速度分辨率均明顯高于時域相關算法的分辨率,實現了目標距離速度聯合超分辨估計,同時可以看出,時域相關算法雖然可以實現目標距離和速度的估計,但是其會產生隨機的旁瓣,從而抬高整個噪聲基底。

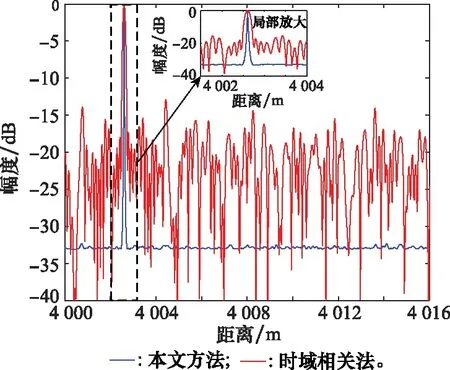
圖6 距離分辨率對比Fig.6 Range resolution comparison

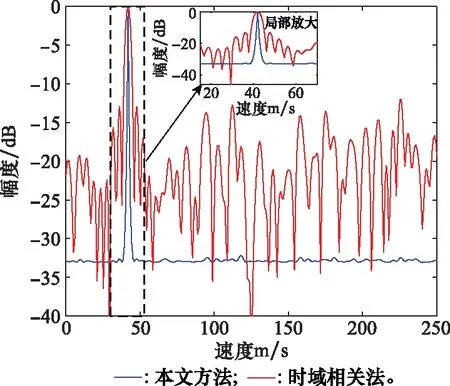
圖7 速度分辨率對比Fig.7 Velocity resolution comparison

3.2 實測數據處理

為進一步驗證所提算法的有效性,對雷達實測數據進行處理,該試驗中雷達發射脈沖的載頻和重頻聯合捷變,脈內調制為線性調頻,雷達觀測場景中存在一個運動目標,雷達工作在Ka頻段,信號脈沖寬度為4 μs,信號帶寬為20 MHz,采樣率為200 MHz,平均脈沖重復周期為30 kHz,跳頻總數為256,跳頻間隔為6 MHz,一個CPI內的脈沖數為64,脈沖的頻率隨機從256個頻點中選取,重頻捷變范圍為0%～30%。

在實測數據處理中,首先將獲取的雷達中頻回波數據根據載頻捷變序列進行數字下變頻,將下變頻后的數據進行脈沖壓縮處理,脈沖壓縮結果如圖8所示。然后，構造矢量a(rg,vg),并利用該矢量構造搜索矩陣。最后，采用MUSIC算法對脈壓后的數據進行處理。值得注意的是,在實際應用中由于器件本身的誤差,雷達產生的載頻-重頻聯合捷變信號會與預設的載頻和重頻有一定的誤差,進而導致在構造搜索矩陣時會產生一定的誤差,從而影響該算法的性能。因此，在實際應用中應根據系統中信號實際的載頻和重頻來構造搜索矩陣,以盡量減少算法的性能損失。實測數據處理結果如圖9所示,從圖9可以看出,目標的估計和速度估計值為[688.1 m,81.85 m/s],采用本文所提方法可以有效地對目標的距離和速度進行估計,實測數據處理結果進一步驗證了該目標參數估計方法的有效性。

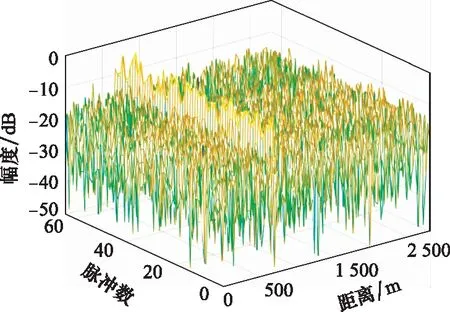
圖8 脈沖壓縮結果圖Fig.8 Results of pulse compression

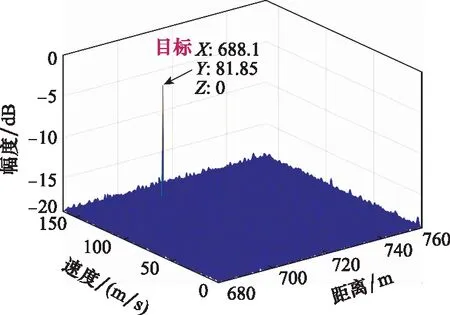
圖9 實測數據處理結果圖Fig.9 Processing results of measured data

4 結束語

本文針對載頻-重頻聯合捷變體制雷達目標參數估計問題,提出了一種基于MUSIC算法的目標參數超分辨估計方法,將陣列信號處理中的超分辨信號處理方法應用到目標參數的估計當中,通過信號模型的空時等效,把目標距離和速度的估計等效成陣列信號處理中二維參數的估計,并將隨機變化的相位項等效成陣列的導向矢量,解決了由于載頻-重頻聯合捷變所帶來的目標參數估計難題,實現了距離和速度的聯合超分辨估計。理論分析和仿真結果表明,本文所提的目標參數估計方法能夠對目標的距離和速度進行聯合超分辨估計,有效提高了對目標的檢測和參數估計能力。