基于LSTM和殘差網絡的雷達有源干擾識別

邵正途, 許登榮, 徐文利, 王晗中

(1. 空軍預警學院信息對抗系, 湖北 武漢 430019; 2. 空軍預警學院雷達士官學校, 湖北 武漢 430300; 3. 國防科技大學電子科學學院, 湖南 長沙 410073)

0 引 言

雷達面臨電子對抗環境日益復雜,各種新型雷達干擾樣式不斷涌現的挑戰[1-2]。有源壓制干擾通過釋放干擾信號壓制雷達目標回波,極大地影響了雷達對目標的探測,給現代雷達的作戰能力帶來了極其嚴峻的挑戰。其主要干擾樣式包括窄帶干擾、寬帶干擾、梳狀譜干擾和掃頻干擾。現代雷達為進行有效地對抗,其先決條件就是對干擾信號正確分類識別,推測掌握干擾方作戰意圖,提升雷達系統對干擾環境的感知能力。因此,干擾類型識別作為抗干擾技術的重要環節一直是研究的熱點[3-4]。目前雷達干擾識別的主流方法是基于信號特征提取的分類方法。影響這類方法性能的主要因素包括兩個方面,一個是特征集的選取及提取,另一個是分類器的選擇。在干擾信號特征的選取及提取方面,由于各類干擾信號具有很強的相似性,單指標特征難以有效完成分類任務,通常采用提取信號時域、頻域、變換域等多維度的多指標特征綜合識別方法,如時頻域內的矩峰度、矩偏度、包絡起伏度、噪聲因子等特征[5-8]、奇異譜特征[9]、雙譜特征[10],這樣一定程度上增加了計算復雜度,造成算法應用泛化能力弱。在分類器的選擇方面,采用較多的是決策樹、K均值聚類[11]、神經網絡[12]、支持向量機[13]分類器。以上這些方法的性能優劣主要依賴于特征提取方法的選擇,耗時且需要專家經驗的輔助,尤其是變換域特征運算量較大,常規分類器分類性能提升空間有限,在強噪聲環境下識別率較低。

近年來,以卷積神經網絡(convolutional neural networks, CNN)為代表的深度學習方法利用其自動特征提取和學習能力在圖像識別、語音處理等模式識別領域得到廣泛應用[14-15],也被相關學者用于雷達及干擾信號的分類識別研究中[16]。文獻[17]基于一維CNN構建雷達干擾信號識別模型。文獻[18]基于干擾信號的時頻圖像利用二維CNN和改進模型,自動學習時頻圖的特征實現干擾信號的分類。文獻[19]利用CNN對脈沖壓縮處理前后的兩個包絡圖和接收波束信號的時頻圖構成的多維特征圖完成干擾分類。以上方法取得了較好的分類效果,但有些只是利用淺層的網絡結構搭建模型,并沒有發揮出CNN特征提取的強大能力。通常來說,網絡層數越深,提取數據隱藏特征的能力越強,但容易出現網絡性能退化問題,殘差網絡很好地解決了這一缺陷。文獻[20]基于擴張殘差網絡實現雷達輻射源信號識別。文獻[21]通過集成殘差塊和非對稱卷積塊提取干擾信號特征,在低信噪比下取得了較好的識別效果。

CNN能夠有效抽取高維數據的隱藏特征,然而循環網絡可以學習到歷史信息,研究表明循環網絡更適合處理時間序列,結合CNN和循環網絡可以發揮兩者的優勢。文獻[22]利用卷積長短時深度神經網絡對輻射源信號的原始時間序列數據進行識別,其模型性能在識別能力上超過單純的長短時記憶(long short-term memory, LSTM)模型。文獻[23]利用CNN和LSTM搭建的深度網絡對振動信號進行分類識別。

針對上述情況,本文在前人研究的基礎上,提出一種殘差CNN結合LSTM的雷達有源干擾識別方法。以干擾信號原始時域波形數據作為模型輸入,利用一維CNN網絡進行信號特征信息提取,殘差網絡提高模型訓練深度避免模型梯度消失,LSTM網絡學習特征時序信息,最終實現信號分類識別,并與單純的殘差網絡和CNN-LSTM等其他深度學習算法進行對比,驗證不同噪聲環境下的識別準確度與計算復雜度。全文共3個部分,第1部分介紹雷達有源干擾信號模型的建立;第2部分在CNN、殘差網絡、LSTM網絡分析的基礎上,介紹本文提出的殘差CNN-LSTM網絡模型搭建的具體方法和結構參數;第3部分是仿真試驗,通過構建信號數據樣本驗證模型的有效性,并與其他深度學習方法進行對比分析。

1 雷達有源干擾信號建模

雷達有源干擾分為壓制干擾和欺騙干擾兩大類,其中壓制干擾主要包括窄帶干擾、寬帶干擾、掃頻干擾、梳狀譜干擾[24]。本文主要針對這4種典型的噪聲壓制干擾信號類型進行分類識別。

窄帶噪聲干擾一般利用噪聲調幅干擾來產生,其表達式為

J(t)=[U0+Un(t)]cos(2πfjt+φ)

(1)

式中:U0是載波電壓;Un(t)是零均值高斯白噪聲;fj為干擾中心頻率;φ為干擾相位在[0,2π]上均勻分布,且和Un(t)是相互獨立的隨機變量。

寬帶噪聲干擾一般用噪聲調頻干擾來產生,其表達式為

(2)

式中:u(t)為零均值平穩隨機過程;KFM是調頻斜率;Uj是干擾的振幅。

利用噪聲調頻波形產生梳狀譜干擾的表達式為

(3)

式中:fj為梳齒出現的頻率點;m為頻率點數目。

掃頻干擾利用一個相對較窄的窄帶信號在一定的周期內重復掃描某個較寬的干擾頻帶產生,表達式為

J(t)=Ujcos[2πfj(t)t+φ]

(4)

式中:fj(t)是干擾信號載頻,隨時間呈現周期性變化。

圖1所示為4類干擾信號在干噪比(jamming-to-noise ratio, JNR)為10 dB時的時域波形,從圖上可以看出各類噪聲壓制干擾信號時域上差異不大,人工分辨較為困難。因此,對于時域波形相似度比較高且對噪聲比較敏感的4類干擾信號,本文利用基于CNN的深度學習模型對干擾信號進行識別。

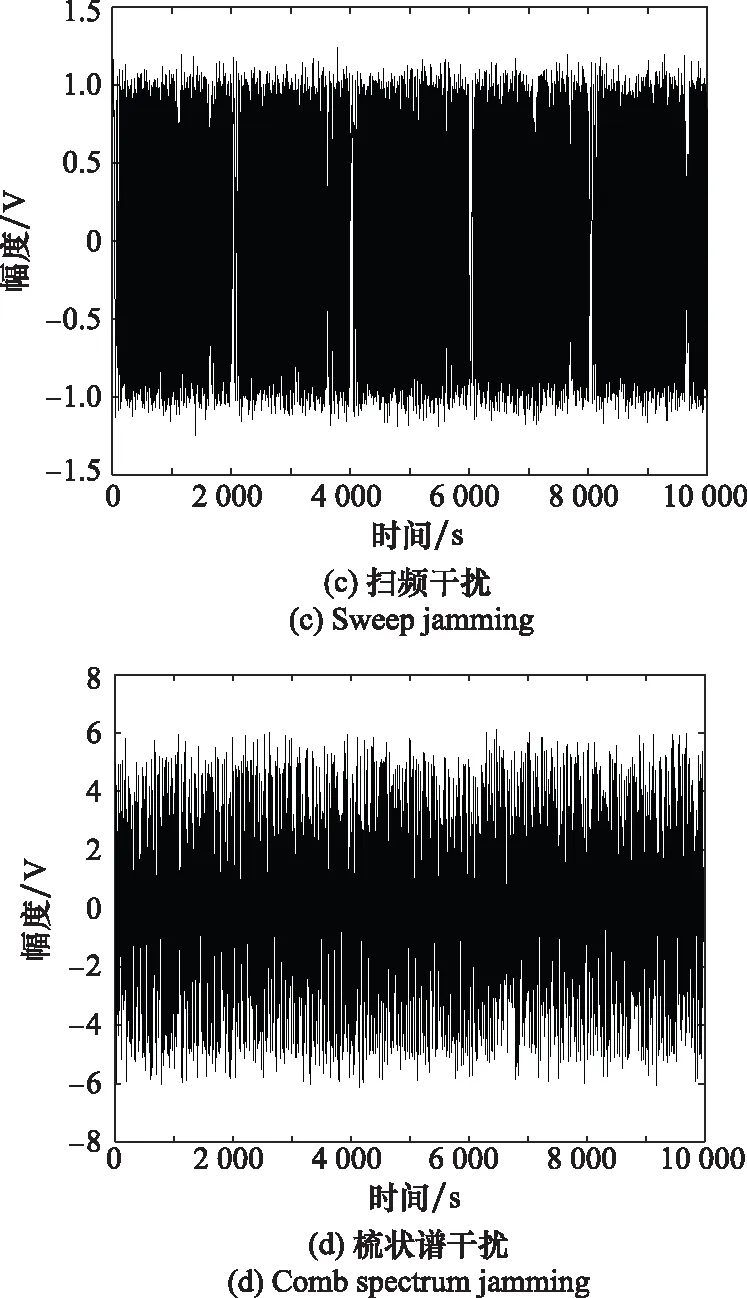
圖1 4類干擾信號時域波形圖Fig.1 Time-domain waveform diagram of four types of jamming signals

2 深度學習模型

2.1 一維CNN

CNN是一種具有表征提取和學習能力的前饋神經網絡,主要由卷積層、池化層和全連接層等組成,在圖像識別等二維數據分類問題中得到了廣泛的應用[25]。卷積層通過卷積核對輸入數據進行特征抽取,在訓練過程中不斷擬合數據局部隱藏特征。池化層對數據進行下采樣降維處理,完成參數稀疏降低數據量。由于輸入數據與卷積核尺寸都比較大,權值和偏置等網絡參數較多,常用參數共享方法,使網絡自由參數的個數減少,加快網絡訓練過程。本文討論的干擾信號時域數據為一維時間序列數據,因此采用一維CNN,其運算公式為

(5)

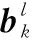
最大池化公式為

(6)

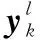
2.2 殘差CNN

隨著CNN模型層數的增加,多個隱藏層之間會帶來特征丟失、信息不完整等問題,從而出現梯度消失現象,降低網絡性能。殘差網絡解決這一問題的主要做法是在卷積處理非線性變換的同時增加線性直達通路[26-27]。其基本單元結構如圖2所示。

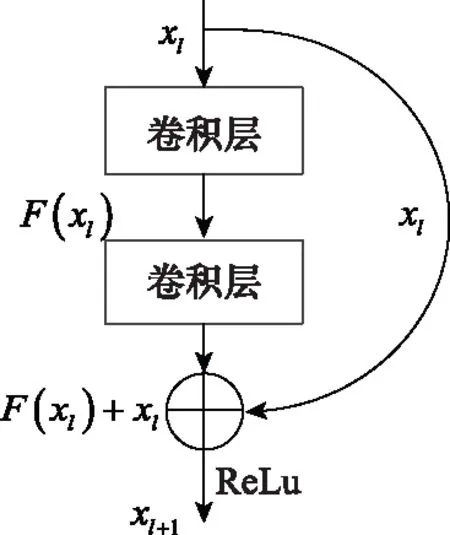
圖2 殘差網絡結構Fig.2 Residual network model

圖2中可以看出,在輸入xl和輸出xl+1之間,中間的兩個卷積層前后設置了越層連接,將淺層的輸入直接連接到端部位置,由于該直達越層連接權重為1,所以可以避免在層層映射的過程中,由卷積層非線性處理F(xl)的權重小于1而導致的網絡梯度消失問題。通過殘差操作,在增加深度的同時也能保證網絡性能不會退化。本文所使用的殘差網絡單元結構如圖3所示,3個卷積層和1個跳線連接構成一個殘差單元。

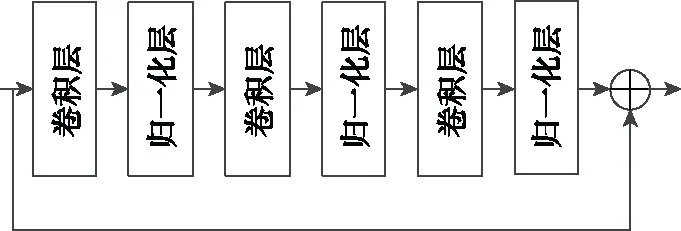
圖3 殘差CNN網絡單元結構Fig.3 Residual CNN network cell structure

2.3 LSTM網絡

循環神經網絡是一種處理復雜序列數據中經常用到的深度學習算法,網絡是以序列數據為輸入,在序列的演進方向上進行遞歸處理,且所有循環單元按鏈式連接的神經網絡,可以處理序列結構的信息,體現信息在時間維度上從前往后的傳遞和積累,能夠擴展時間特征。常規的循環神經網絡每個時刻的隱藏層狀態由當前輸入和前隱藏層的狀態同時決定,記憶容量有限而且容易造成梯度消失的問題。LSTM網絡在常規循環神經網絡的基礎上引入了遺忘門、輸入門、輸出門單元來控制LSTM單元的狀態迭代,通過門系數來控制記憶信息、輸入信息的獲取和輸出信息的傳輸,提高分類網絡的效能和穩定性[28-30],如圖4所示。

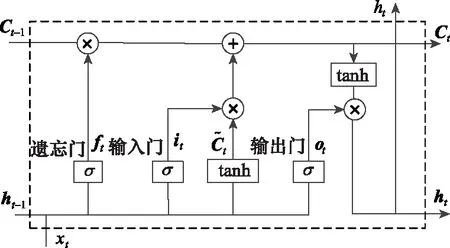
圖4 LSTM單元的基本結構Fig.4 LSTM cell structure

LSTM與一般循環神經網絡的不同主要在于遞歸網絡隱藏狀態的計算,t時刻LSTM單元狀態Ct由舍棄單元無用信息和保留部分有用信息兩部分決定,該時刻隱含層的狀態ht由輸出門挑選Ct的有用信息得到,其計算式分別為

ht=ottanh(Ct)

(7)

(8)

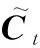
ft=σ(Wf×[ht-1,xt]+bf)

(9)

it=σ(Wi×[ht-1,xt]+bi)

(10)

ot=σ(Wo×[ht-1,xt]+bo)

(11)

(12)

式中:Wf、Wi、Wo為各門控節點的權值矩陣;Wc代表記憶權重;bf、bi、bo為各門控節點的偏置;bc代表記憶單元偏置;σ代表sigmod函數。

LSTM通過輸入門、遺忘門、輸出門這3個門實現了其特殊的長短期數據記憶功能,使得該模型更適合學習前后關聯和連續性的數據的特征。干擾信號時域數據具有時間連續性,選用具有記憶功能的LSTM模型符合本文研究的干擾信號分類要求。

2.4 干擾信號分類模型

本文構建基于殘差CNN和LSTM的深度學習分類網絡結構如圖5所示,網絡結構參數如表1所示。模型共有33層,其工作過程如下:

步驟 1由于LSTM層的輸入為序列數據,所以首先將干擾信號時域數據進行序列折疊輸入后續網絡層;

步驟 2通過一次卷積和兩次殘差塊操作,再經過最大池化層和扁平層將數據進行降維和壓平;

步驟 3將扁平層輸出數據進行序列展開輸入兩層LSTM層進行時序信息提取,最終得到提取的特征。

步驟 4利用Softmax輸出概率值,根據概率分布確定信號的類型,并根據標簽輸出正確率。

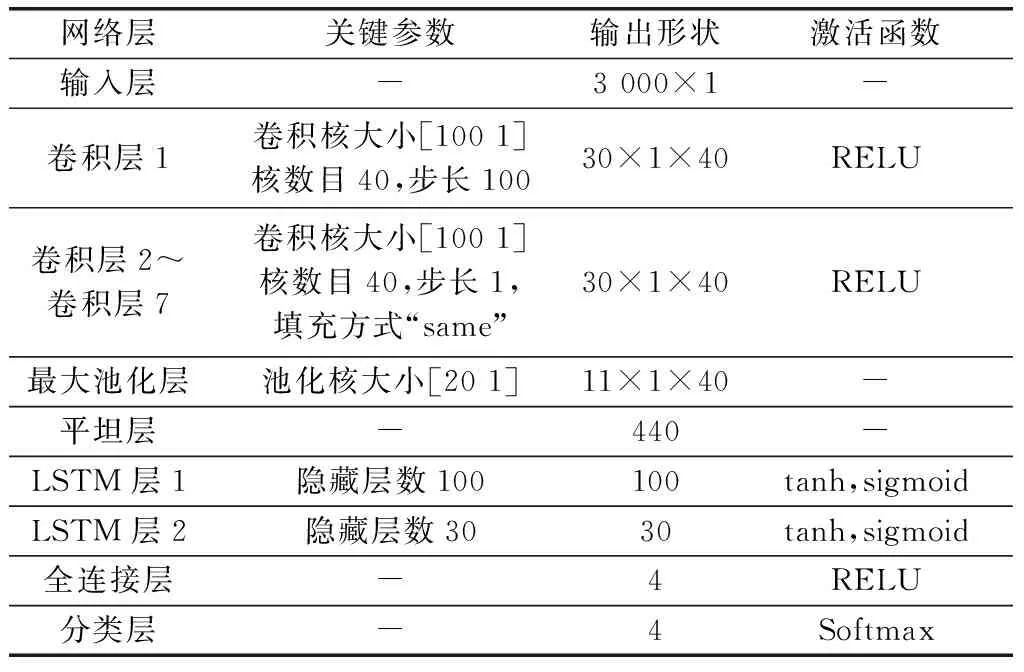
表1 網絡結構參數

圖5 殘差CNN-LSTM深度學習網絡模型Fig.5 Residual CNN-LSTM deep learning network model

3 仿真試驗

3.1 試驗流程

基于LSTM和殘差CNN的深度學習網絡的干擾信號識別試驗流程如圖6所示,干擾信號訓練和測試樣本數據產生以及網絡模型的搭建、訓練和測試均在Matlab2019環境下進行,操作系統為Windows 7旗艦版64位操作系統,CPU為Inter(R) Core(TM) i7-1165G7 2.80 GHz,GPU為NVIDIA GeForce MX450,運行內存為16.0 GB。

圖6 基于深度學習網絡的干擾識別框架Fig.6 Jamming recognition framework based on deep learning network

3.2 仿真條件

本文基于干擾信號的時域仿真數據,構建一維殘差CNN與LSTM的干擾信號識別模型。對窄帶干擾、寬帶干擾、梳狀譜干擾、掃頻干擾4種信號,在JNR為-10～10 dB的范圍內,JNR間隔為2 dB,每類信號每個JNR下產生100個訓練樣本。干擾信號采樣頻率fs為100 MHz,干擾持續時間τs為30 μs,4類信號的參數如表2所示,所有參數在取值范圍內隨機選取。對算法進行測試時,在每個JNR下各產生100個測試樣本用于測試。

表2 4類信號參數設置

續表2

3.3 仿真結果

為提升訓練效率,實驗中設置的迭代次數為30次,每批次訓練樣本數量為500。同時為了驗證本文提出的殘差CNN-LSTM深度學習模型對干擾信號識別的有效性,將本文方法與殘差CNN和CNN-LSTM網絡兩種方法進行對比分析,其網絡結構分別如圖7和圖8所示,模型中的參數和表1中所列相同。

圖7 殘差CNN網絡模型Fig.7 Residual CNN network model

圖8 CNN-LSTM網絡模型Fig.8 CNN-LSTM network model

通過500次蒙特卡羅實驗得到的信號識別率結果如圖9所示,分別為殘差CNN-LSTM、殘差CNN、CNN-LSTM在不同JNR下測試集中的準確率。從圖9中可知,在測試過程中,3種深度學習網絡對信號的識別準確率均隨JNR的增大而提高,其中綜合利用殘差和LSTM的深度學習網絡對于各JNR環境下的干擾信號識別性能要普遍優于其他兩種網絡。測試集中在JNR為0 dB的強噪聲環境下,殘差CNN-LSTM方法對4種干擾信號識別準確率均大于98.3%,其中對寬帶干擾和窄帶干擾的識別率可達100%。殘差CNN網絡的表現略差,在JNR為0 dB時,對4種干擾信號識別準確率均大于95.2%,但在更低JNR環境下和殘差CNN-LSTM網絡性能差距拉大,-4 dB下最低識別率僅為78.5%,殘差CNN-LSTM網絡表現更為穩定,4類信號最低識別率為91.2%。CNN-LSTM網絡的準確率表現最差,在JNR為0 dB的環境下,4種干擾信號準確率最低為90.8%。說明通過殘差網絡和LSTM網絡的引入,CNN網絡的表現更為穩定,魯棒性更好,強噪聲環境下準確率有明顯提升。

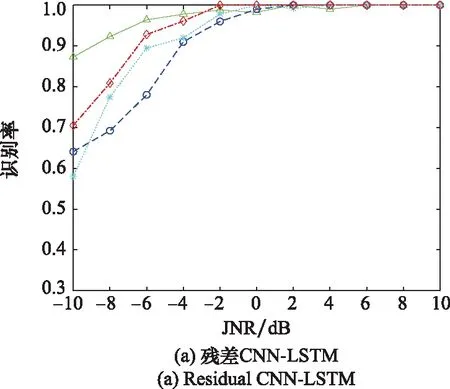
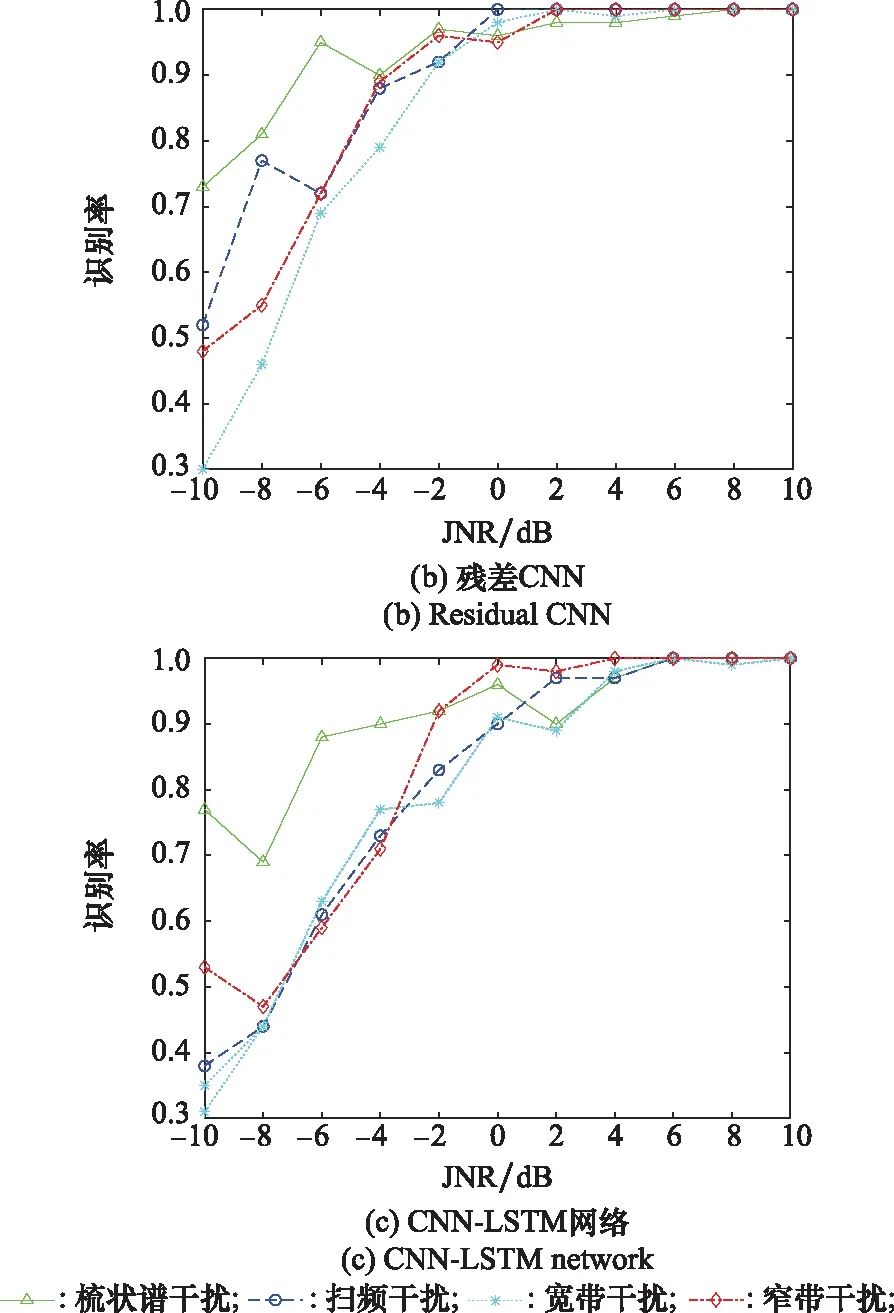
圖9 不同JNR環境下4類信號識別準確率Fig.9 Recognition accuracy rate of four types of signals under different JNR environments

圖10為3種深度學習網絡在訓練過程中準確率、損失率變化曲線的比較。可以看出,3種網絡均具有較穩定的網絡性能,其中本文提出的殘差CNN-LSTM網絡的收斂速度最快,在相同的迭代次數下,準確率和損失率均優于其他兩種網絡結構下的數值,也體現了在深層模型下殘差網絡模型和LSTM網絡模型結合的優勢。

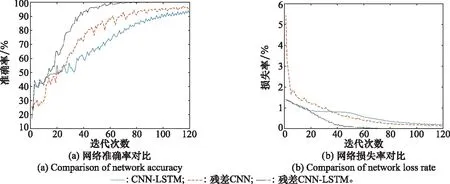
圖10 3種網絡測試集學習損失率、準確率變化圖Fig.10 Learning loss rate and accuracy rate change diagram of three network test sets

3.4 模型可視化

為直觀呈現殘差CNN-LSTM模型各層數據的分布情況和網絡迭代性能,采用T-分布隨機近鄰嵌入(T-distributed stochastic neighbor embedding, T-SNE)方法對各個層輸出的高維特征進行降維,并在二維平面進行可視化。圖11為4 400個訓練樣本經卷積層、LSTM層輸出后經過降維處理后的散點分布圖。圖11中,序號1～4分別代表窄帶干擾、寬帶干擾、梳狀譜干擾和掃頻干擾4類信號,橫縱坐標軸表示數據降維后的兩個特征。從圖11可知,從原始信號的第一層卷積層提取的特征難以區分不同的干擾類型(見圖11(a))。隨著網絡層的不斷迭代,不同網絡層學習出來的數據特征逐漸呈現出獨特的聚集分布,最終實現準確可靠的分類(見圖11(i))。

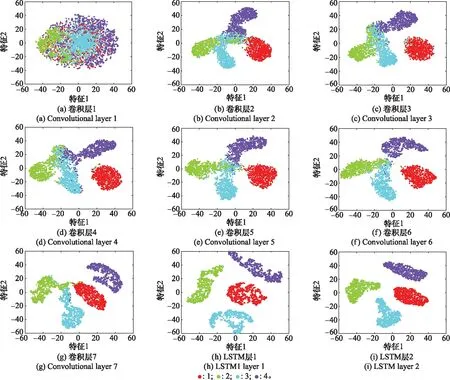
圖11 訓練集樣本各網絡層T-SNE降維可視化情況Fig.11 T-SNE dimensionality reduction visualization of each network layer of the training sets sample

3.5 計算復雜度分析

神經網絡的復雜度主要包括空間復雜度和時間復雜度,空間復雜度是指網絡可學習參數量,主要由卷積層、LSTM層和全連接層決定。時間復雜度從每輪訓練迭代時間和單個樣本平均識別時間兩方面進行分析。在500次蒙特卡羅實驗統計平均情況下,本文采用的殘差CNN-LSTM和殘差CNN、CNN-LSTM的復雜度對比如表3所示。

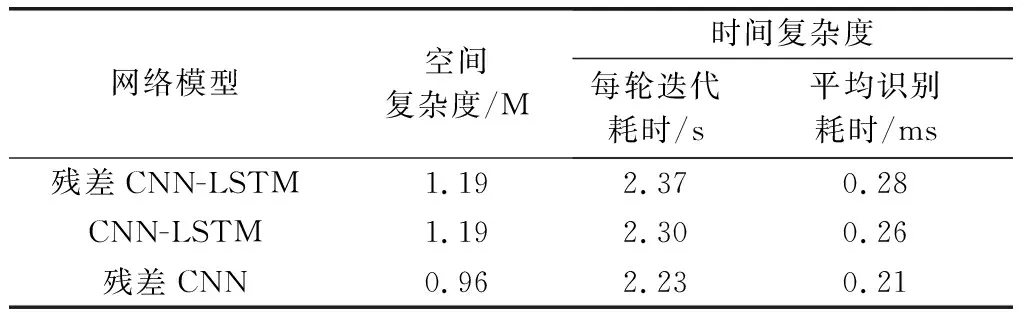
表3 模型復雜度對比

由表3可知,殘差CNN-LSTM的空間復雜度和時間復雜度與CNN-LSTM基本一致,由于增加了LSTM層,網絡結構更為復雜,其參數量相比殘差CNN有一定增加,空間復雜度高于殘差CNN,每輪迭代耗時和平均識別耗時也略高于殘差CNN。但從表3中數據來看,本文提出的殘差CNN-LSTM在空間復雜度和時間復雜度與殘差CNN、CNN-LSTM相比差別不大,識別耗時均在ms量級,且殘差CNN-LSTM模型能夠取得更高的識別正確率。

4 結 論

本文提出了基于一維殘差CNN和LSTM網絡結合的干擾信號分類方法。該方法直接利用干擾信號時域數據提取信號高維抽象特征,避免了人為提取信號特征的預處理環節,可以實現對4類雷達有源噪聲干擾信號的有效分類,在低JNR下也能提供可靠的識別率,4類信號在JNR為0 dB的強噪聲環境下信號識別準確率均高于98.3%。

本文所提方法通過在模型中引入殘差網絡提高了網絡深度,利用LSTM網絡對時序信息的提取能力提高了模型的抗噪性能。通過對3種深度學習網絡的對比試驗表明,殘差CNN-LSTM網絡在各JNR環境下的分類性能和魯棒性最佳,在相同的迭代次數下,準確率和損失率均優于其他兩個網絡結構下的數值,體現了在深層模型下殘差網絡模型和LSTM網絡模型結合的優勢。