基于模糊約束的貝葉斯網絡參數學習

茹鑫鑫, 高曉光, 王陽陽

(西北工業大學電子信息學院, 陜西 西安 710129)

0 引 言

貝葉斯網絡(Bayesian network,BN)[1]已經成為表示和處理不確定信息的有效工具,一個完整的BN包括一個有向無環圖(directed acyclic graph,DAG)和對應的條件概率表(conditional probability table,CPT),分別從定性和定量角度表示出節點之間的依賴關系。目前BN已經在故障診斷[2]、基因分析[3]等領域有了廣泛應用。

通常BN的結構[4-6]和參數[7-10]都是從數據中學習得來,當數據充足時,K2[11]是常用的結構學習算法,最大似然估計(maximum likelihood estimation,MLE)算法[12]是常用的參數學習算法。當訓練樣本量難以滿足學習需求時,僅利用K2算法和MLE算法會造成學習結果過擬合,無法得到精確的結構和參數。對于該問題,在結構學習中,專家可以直接給出節點間的定性關系,但在參數學習中,專家難以給出準確的參數值。目前,相關研究主要通過基于約束的方法、數據擴展以及兩者混合的方法來解決這一問題。基于約束的方法主要有兩種:凸優化(convex optimization,CO)[13-14]和定性最大后驗(qualitative maximum a poste-rior,QMAP)估計[15-18]。CO將參數學習問題轉化為在約束空間內尋找目標函數最優解。約束MLE(constrained MLE,CMLE)是將MLE與約束條件相結合來構建CO優化模型。QMAP首先利用蒙特卡羅方法生成滿足約束條件的先驗參數,再構建超參進行最大后驗(maximum a posterior,MAP)估計。基于數據擴展的方法力求通過增加樣本量來解決數據不足的問題。文獻[19]使用遷移學習來增加數據量,當目標網絡和源網絡具有相同的結構時,直接遷移數據進行參數學習。文獻[20]用額外的數據源解決了節點樣本完全缺失的參數學習問題,通過元分析法結合多源樣本來學習參數。文獻[21]認為在多樣本條件下,低質量樣本在參數學習中不應與高質量樣本擁有相同的權重,通過使用馬氏距離對樣本進行評分加權學習。對于約束與數據擴展混合的方法,文獻[22-23]通過不等式約束判斷備選源域的樣本是否可以被遷移,通過范圍約束確定備選源域在遷移學習中的權重,從而提高樣本遷移準確度。文獻[24]提出了一種基于約束的參數擴展方法,通過自助法擴展數據產生滿足約束條件的參數進行學習。

盡管約束在參數學習中已經得到了廣泛應用,但如何平衡約束干預學習過程的過擬合和欠擬合仍然是一個亟待解決的問題。在小樣本量下,如果參數學習完全依靠數據,就會出現因樣本不足而造成的參數學習結果過擬合問題。對于基于約束的MAP方法,不論其約束形式和先驗參數量化方式有何不同,都需要構建Dirichlet超參來實現參數學習。當約束的干預效能較低時,即選取的超參值較小,難以消除學習結果的過擬合。當約束干預過強時,即選取的超參值過大,學習結果會完全偏向約束,造成學習結果欠擬合。假設專家對一個約束條件有90%的把握,而對另一個約束條件只有60%的把握,如果這兩個約束在學習過程中有相同的超參值也是不合適的。因此,如何讓約束在學習過程中發揮適當角色,關鍵是構建合適的超參。

本文核心思想是對于同一約束,專家把握度(隸屬度)越大對應的超參值應該越大;對于同一約束,給定學習樣本為100所對應的超參應大于給定學習樣本量為300的超參,即給定的樣本量越大,對應的超參應該越小。

綜上,本文提出基于模糊先驗約束的BN參數學習算法,通過將隸屬度引入到超參的構建過程中,解決小樣本下參數學習的過擬合問題。同時,引入樣本量邊界來避免因外界過度干預而造成參數學習結果的欠擬合問題。此外,將本文所提算法應用到網絡安全評估中,以漏洞評分作為先驗信息,結合遷移學習思想,利用漏洞編號進行遷移學習。

1 預備知識

1.1 參數學習

BN結構描述節點間的定性關系,參數表達節點的概率分布。因此,BN是由一個DAG和對應的CPT組成的。BN可以定義為G(V,E),其中,V1,V2,…,Vn∈V是網絡中的節點集合,E是邊集合。給定任意節點Vi的父節點集合Πi,Vi獨立于其非子孫節點。當訓練數據充足時,MLE是常用的參數學習方法,其目標函數[17]可以表示為

(1)

式中:θ為整個BN的參數;θijk表示網絡中節點Vi的父節點Πi為第j個組合時,i取值為k的參數,即P(Vi=k|Πi=j);ri為節點的狀態數,為父qi節點Πi組合數;Nijk代表數據集D中網絡中節點Vi的父節點Πi為第j個組合時的統計樣本量;c為一個常量。最大化式(1)之后,θijk的MLE可以表示為

(2)

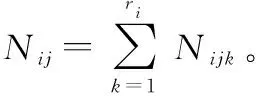
當學習樣本量不足時,使用MLE容易造成學習結果過擬合,無法得到準確的參數。為解決此問題,通常將先驗信息融入到參數學習中來提高學習精度。此時,參數學習問題便轉化為融合先驗信息后的MAP問題[13],如下所示:

(3)

式中:αijk為節點Vi的父節點Πi為第j個組合狀態時,i取值為k的超參,αijk為Dirichlet分布。超參可以消除過擬合的原因在于αijk作為虛擬樣本量進行參數學習,最大化式(3)后,可以得到θijk的MAP估計如下所示:

(4)

式中:αij為節點Vi的父節點Πi為第j個組合狀態時的超參權值。

1.2 常見約束形式

專家可以依據在專業領域中的理論和經驗積累,對BN參數做出一些約束判斷,這些判斷可以轉換為參數學習過程中的約束條件。常用的約束形式如下。

(1) 范圍約束

定義一個參數范圍約束空間如下所示:

0≤α≤θijk≤β≤1

(5)

式中:α和β是約束范圍的邊界。

(2) 不等式約束

定義兩個參數之間的大小關系如下所示:

θijk<θij*k*

(6)

式中:θij*k*為與θijk存在不等關系的參數。

(3) 近似相等約束

定義兩個參數的近似相等關系如下所示:

|θijk-θijk*|≤δ

(7)

式中:δ為置信區間。

(4) 公理約束

定義參數最基本的概率性質,即歸一化和非負性如下所示:

(8)

2 基于模糊約束的參數學習

2.1 模糊超參構建

基于約束的MAP方法是在給定訓練樣本之后,利用約束來對學習過程進行干預。不論約束形式和先驗參數量化方式有何不同,最終都需要構建超參來進行學習。如果完全依賴約束,此時式(3)可以寫為

(9)

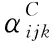
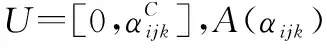
(10)

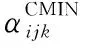
(11)

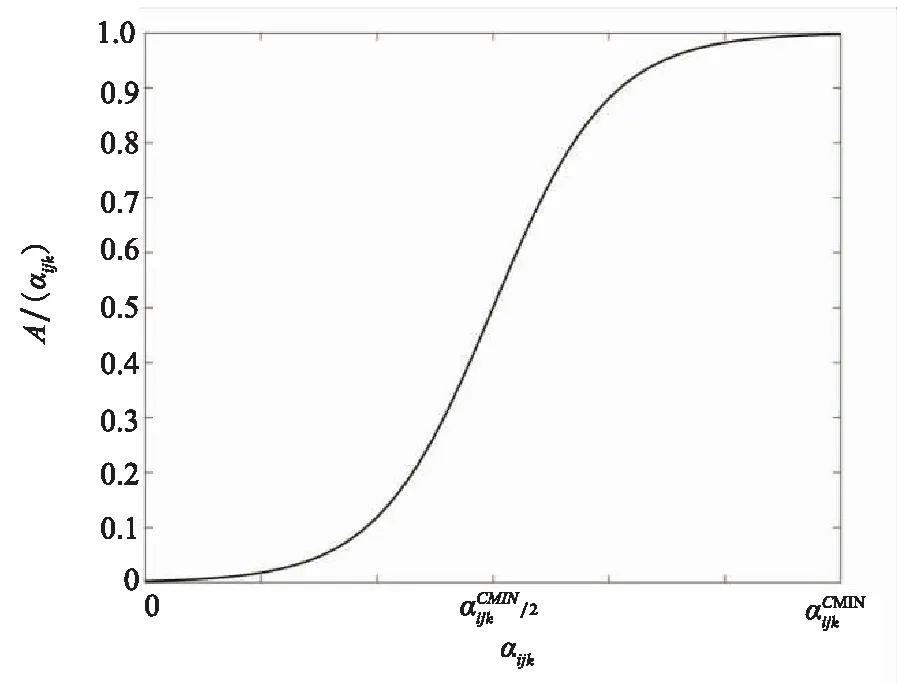
圖1 超參隸屬度分布圖Fig.1 Hyperparameter membership distribution chart

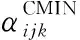
(12)

式中:Ω為參數約束集合。當同分布中,ri比較大時,式(12)難以求解,因此可以將MAP改寫來求解,如下所示:

(13)

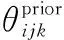
(14)

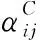
(15)

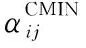
(16)

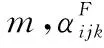
(17)

綜上,本文提出的模糊MAP(fuzzy MAP, FMAP)估計的計算方法為

(18)

2.2 FMAP估計

由于約束難以完全覆蓋BN中每一個參數,當無約束時,平滑先驗和貝葉斯狄利克雷似然等價一致聯合分布(Bayesian Dirichlet with likelihood equivalence and a uniform joint distribution，BDeu)是常用的先驗分布,解決了由樣本不足造成的參數結果為0的問題,一定程度上提高了參數學習的精度。無約束下MAP計算方法如下所示:

(19)

式中:當λ=1時,為平滑先驗;當λ=(riqi)-1時,為BDeu先驗,本文選擇λ=1。

綜上,本文提出的FMAP估計方法如算法1所示。

算法1FMAP輸入 約束Ω,訓練數據D輸出 參數 θ1. For each Vi of BN2. For each j of Πi3. For each k of ri4. If θijkis not constrained∥如果不存在約束5. θijk←式(19);∥θMAPijk為最終參數6. Else7. θMLEijk←式(2);∥θMLEijk為最終參數8. If θMLEijk∈Ω∥如果θMLEijk符合約束9. θijk←θMLEijk;∥θMLEijk為最終參數10. Else11. θpriorijk←Ω;∥約束量化出先驗參數θpriorijk12. αCij=1;13. While (θijk?Ω)∥交叉驗證求式(14)中 αCMINij14. αCMINij=+1;15. θijk=Nijk+ αCMINijθpriorijkNij+ αCMINij;16. End While17. αFij←式(16);18. For each k of ri∥參數歸一化19. θijk←式(18);∥θFMAPijk為最終參數20. End For21. End If22. End If23. End For24. End For25. End For

3 實驗驗證

3.1 實驗設置

實驗代碼基于BNT工具進行實現,運行在Matlab 2020上,實驗硬件配置為CPU AMD 5950X和RAM 32G。實驗選取6個不同規模的標準BN,通過對比不同算法來驗證FMAP的有效性。標準BN[26]信息如表1所示,根據參數數量可將實驗標準網絡分為小、中、大。

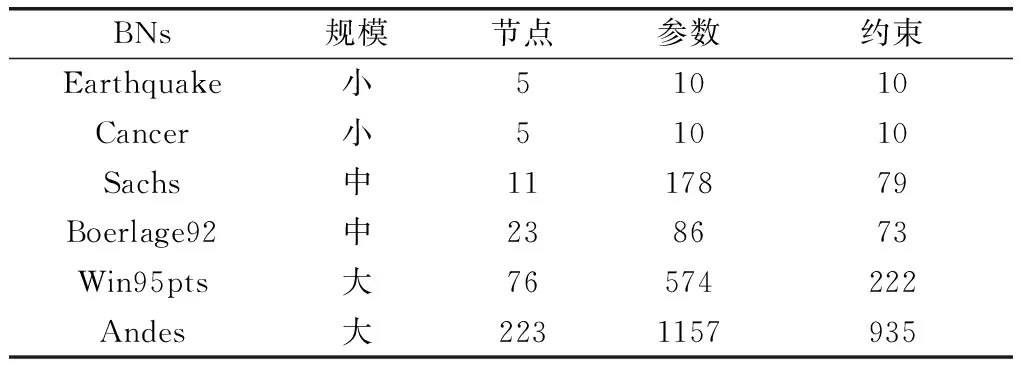
表1 標準BN信息

標準BN的結構和網絡參數是已知的,訓練數據是由BNT[27]工具箱提供的“sample_bnet”函數根據標準BN產生。進行對比實驗算法如下:

(1) MLE:純數據驅動的學習方法,不融合任何先驗信息;

(2) MAP:融合先驗的參數學習方法,使用平滑先驗,即αijk=1;

(3) CMLE:結合約束與CO的方法;

本文實驗通過相對熵又稱KL(Kullback-Leibler)散度[28]來評價標準網絡參數和學習結果之間的誤差,KL值越低說明學習結果精度越高,KL計算方法如下所示:

(20)

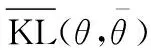
圖2展示了Cancer網絡的結構和每個節點對應的CPT表。依據約束構建原則和圖2中節點的CPT表,構建出表2中Cancer網絡的正常約束,即η=0,本文實驗中的其他BN約束的構建方式與Cancer相同。

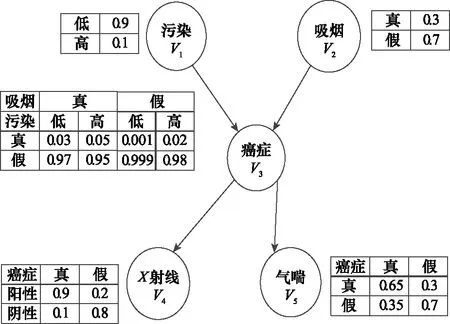
圖2 Cancer網絡結構和參數Fig.2 Cancer network structure and parameters

表2 Cancer網絡約束

本文主要研究的是小樣本下參數學習精度問題,為此實驗樣本量設置為100、300、500。通常小樣本下參數學習研究的訓練樣本量設置為50到500,對于小型網絡,500樣本量依然被認為是不充足的。而Cancer 和Earthquake 參數個數都為10,1 000樣本量已經相對充足,在文獻[5]中對于大型網絡,認為10 000為相對充足的樣本量。因此,對式(17)中的M,小型網絡設置為M=1 000,中型網絡為M=5 000,大型網絡為M=10 000。為得到更加穩定準確的實驗結果,每個學習案例重復學習20次。每次都重新生成訓練數據,20次實驗的方差也將在結果中顯示。對于每個學習案例，性能表現最好的算法結果在表格中加粗表示。

3.2 算法精度驗證

本部分實驗主要驗證在正確約束環境下,即所有約束η=0,FMAP算法是否可以有效提高參數學習的精度。學習結果如表3～表5所示。

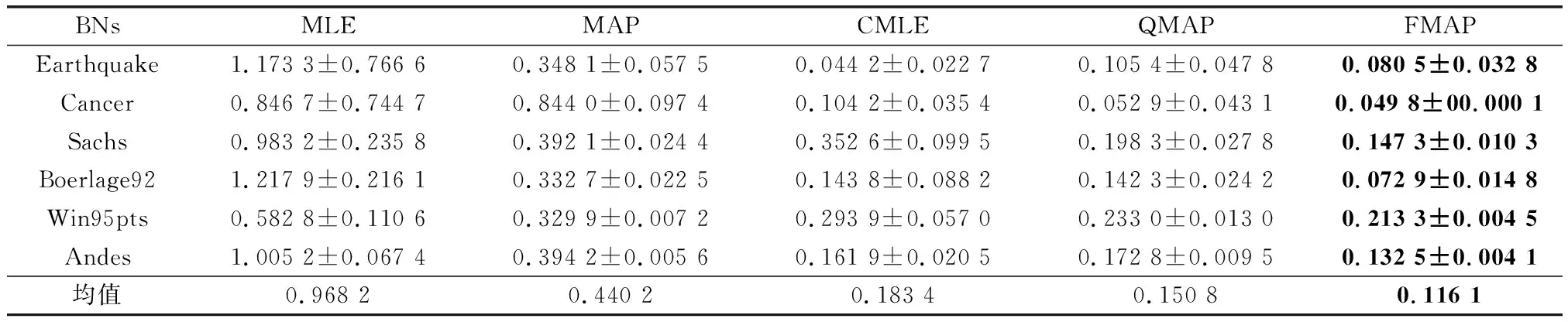
表3 100樣本量KL對比

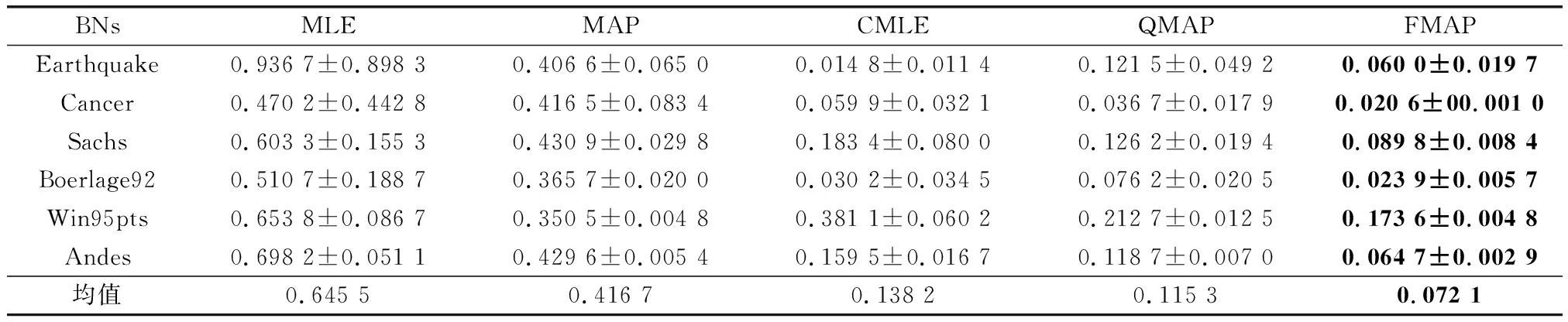
表4 300樣本量KL對比

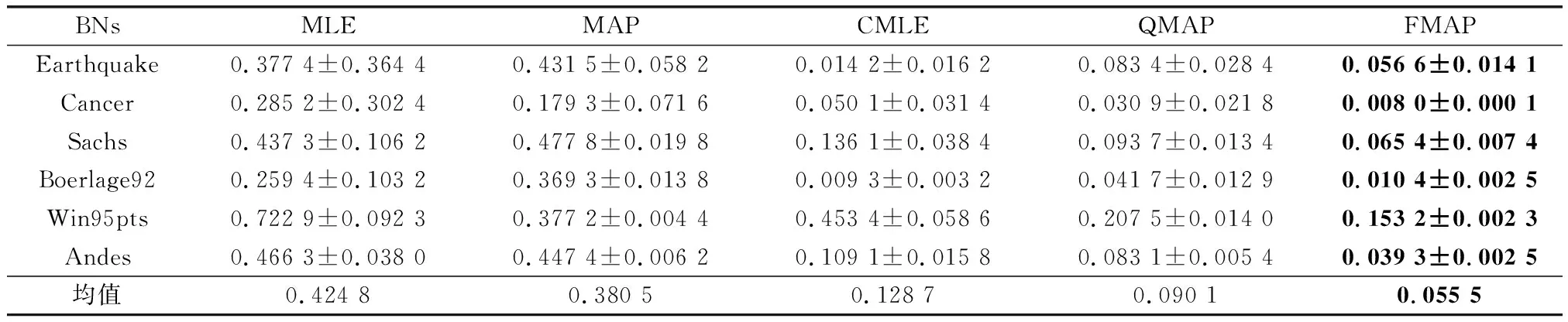
表5 500樣本量KL對比

通過表3～表5結果可以發現，在正確約束實驗中,FMAP的精度表現最好。增加先驗的MAP與純數據學習的MLE相比,在3個樣本量下精度分別提高了54.3%、35.45%、10.42%。MLE雖然有不錯的收斂性,隨著訓練樣本量的增加與MAP的差距逐漸減少。但在小樣本量下,由于容易出現一些參數沒有學習樣本的情況,導致參數結果為0,而MAP引入平滑先驗,有效地解決了這一問題。結合約束的CMLE與MLE相比,在3個樣本量下精度分別提高了81.06%、78.60%、69.70%。同樣，結合約束的QMAP與MAP相比,在3個樣本量下精度分別提高了65.7%、72.3%、76.3%。由此可以看出,加入先驗和結合約束可以提高參數學習的精度。QMAP與CMLE相比，在3個樣本量下精度分別提高了17.77%、16.57%、29.90%。構建模糊超參的FMAP與固定超參權值的QMAP相比,在3個樣本量下精度分別提高了21.01%、37.47%、38.40%。

實際應用中,通常會有噪音的存在,這將挑戰算法的魯棒性。本文部分實驗,將在約束中混入20%的一般噪音約束(η=0.2)和10%的極端噪音約束(η=0.4)來進行學習,以驗證算法的魯棒性。本部分實驗,只針對基于約束的算法進行對比。

通過表6～表8可以發現在噪音約束下,QMAP與CMLE相比精度分別提高了75.5%、67.18%、50.46%;FMAP與QMAP相比精度分別提高了27.1%、39.36%、46.79%。因此,在噪音約束環境中,FMAP依然有杰出的精度表現。通過與正確約束中的3個算法的學習效果比較發現,CMLE受噪音約束影響最嚴重,QMAP次之,FMAP受到的影響最小。造成這一結果的原因是,CMLE是以約束為導向,構造目標函數來學習,對約束的依賴性極強。因此CMLE容易受到約束質量的影響,而CMLE本身并沒有相關的設計來應對這一問題。對于QMAP超參權值使用節點狀態的勢,設置相對固定,既不能在正確約束中發揮足夠的干預效果,也不會過分受到噪音約束影響。而本文提出的FMAP通過引入模糊理論,提高了約束使用的精準度和可解釋性,為超參的構建提供了更加靈活的方法。

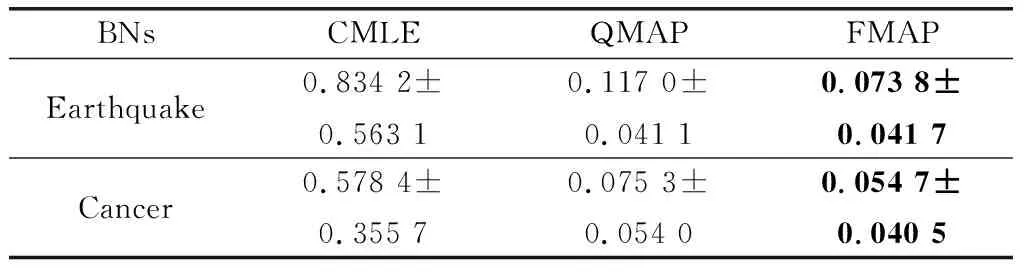
表6 噪音約束下100樣本量結果對比

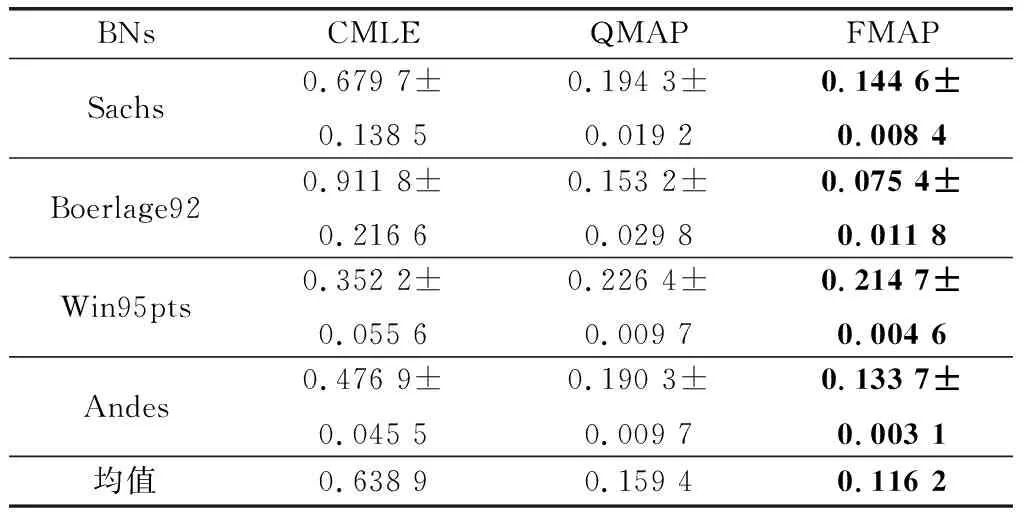
續表6

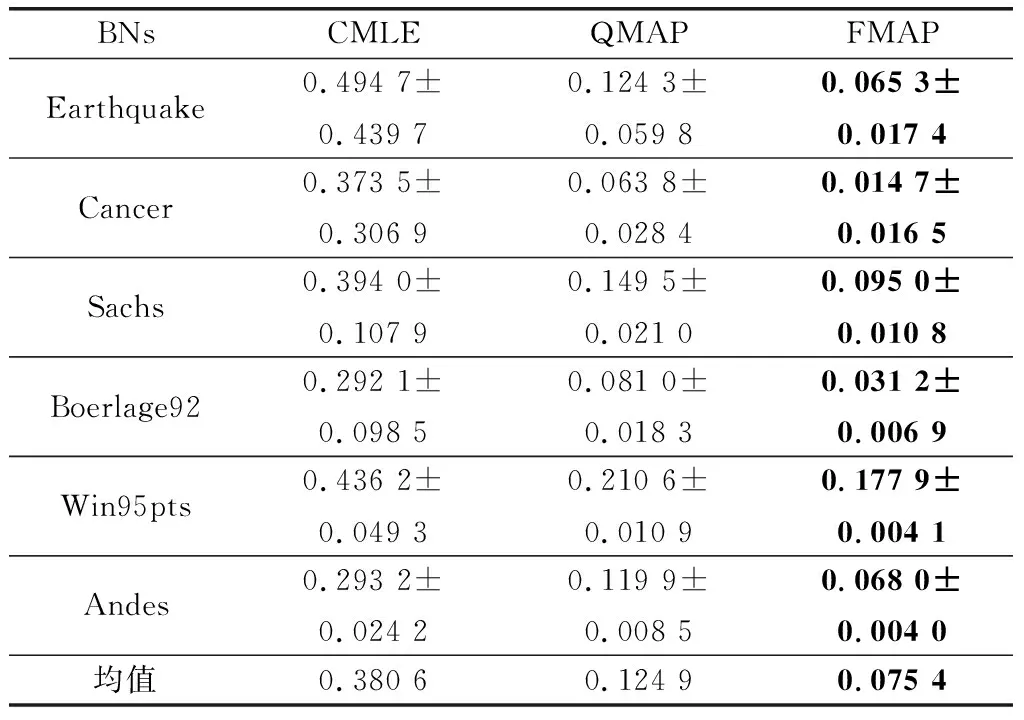
表7 噪音約束下300樣本量結果對比

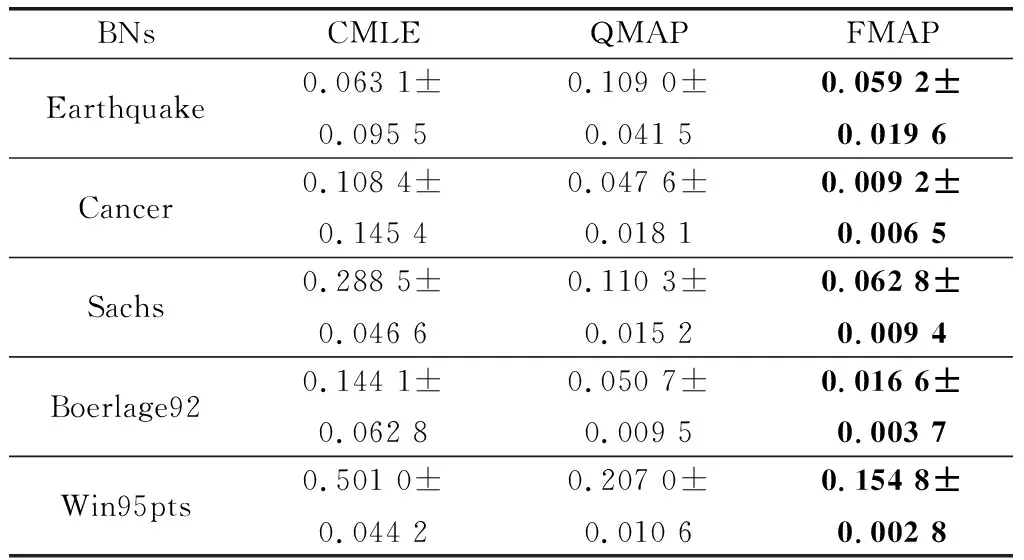
表8 噪音約束下500樣本量結果

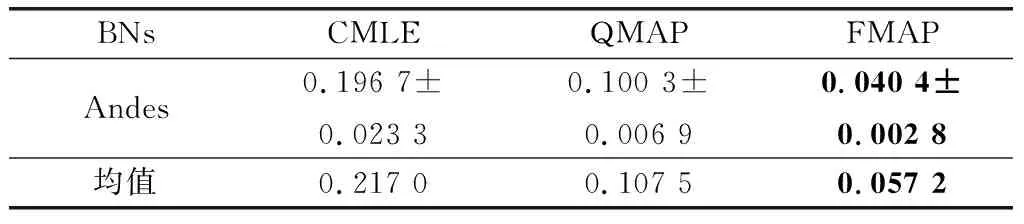
續表8

3.3 算法時間驗證

精度和時間是檢驗算法常用的指標,上文對算法的有效性和魯棒性進行了驗證,本部分將對算法運行時間進行分析。為節省篇幅,本文只展示最有代表性的最小樣本量和最大樣本量的結果,如表9和表10所示。通過表9和表10可以看出,對學習過程不做任何干預的MLE運行時間最優,本文提出的FMAP算法排在第4位,消耗時間最多的算法是CMLE。CMLE更多的時間消耗在構建CO和求解上,QMAP在先驗參數的量化過程中消耗了一定的時間,FMAP需要更多的時間來處理交叉驗證和模糊超參求解。而本文是解決小樣本下的參數學習問題,在實驗樣本為500時,即使對于最大的標準網絡Andes的算法運行時間,FMAP也僅為2.38 s,運行時間雖然為MLE的1.98倍,但也是僅多消耗了1.18 s,比QMAP多消耗了0.77 s。對于小樣本下參數學習這一特殊的問題,多數算法的運行時間都在可接受范圍之內,因此FMAP所多消耗的時間是可以接受的。

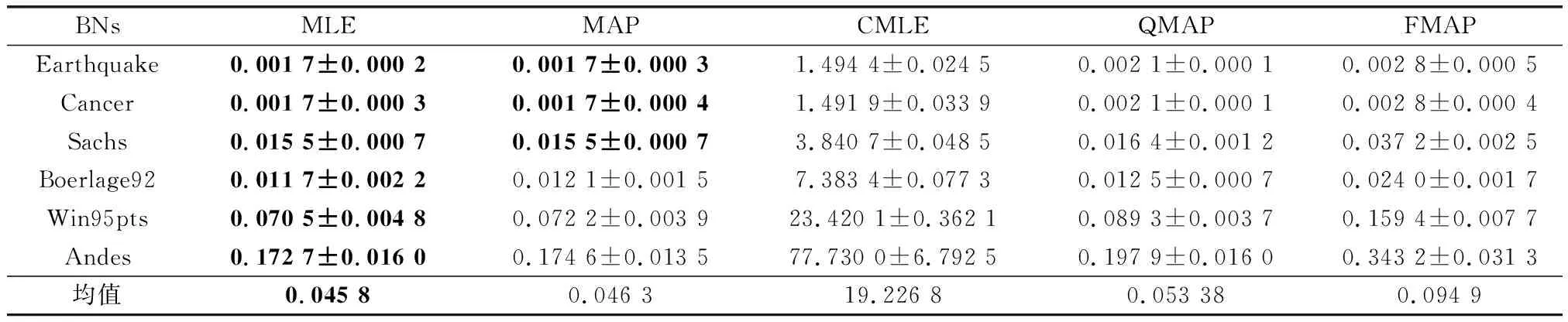
表9 100樣本量下各算法運行時間

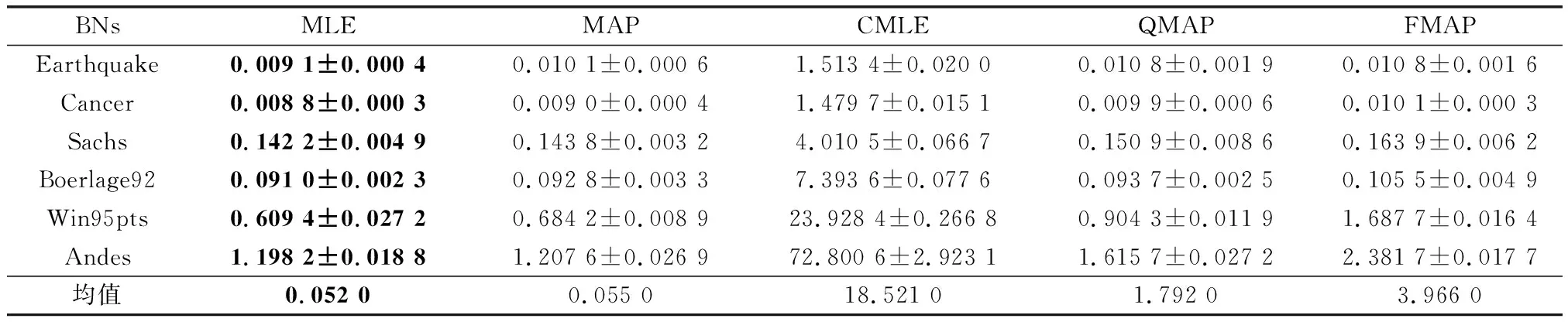
表10 500樣本量下各算法運行時間

4 基于FMAP的網絡安全評估

4.1 基于FMAP的網絡安全評估方法

BN在網絡安全領域中的應用,主要是結合攻擊圖模型,進行網絡安全預測評估。但由于待評估目標網絡中歷史數據獲取困難,網絡參數基本依靠專家經驗來得到。參數主觀性強,導致之后評估結果的客觀性不足,如何獲取更加客觀準確的參數是目前網絡安全評估領域所要解決的問題之一[29-31]。網絡攻擊主要通過漏洞來進行,但各種因素導致網絡漏洞無法完全修復,從而為攻擊的發生提供條件。網絡的拓撲圖可以認為是確定的BN結構,網絡中的漏洞為BN中的節點,節點間的因果關系由物理連接所確定。

遷移學習[23]是將已得到的知識,應用到新的問題上,核心是找到已有知識和新問題之間的相似性。遷移學習可以分為基于樣本的遷移、基于特征的遷移、基于模型的遷移,以及基于關系的遷移。本文使用的是樣本遷移,將相同漏洞的數據遷移進行學習。BN攻擊圖中只考慮遷移樣本和節點參數為Πi=1的情況,對于網絡攻擊圖而言,Πi的特殊之處為任意父節點為1即可,即Πi節點狀態或關系為1,并不考慮Πi=0的情況,即Πi所有節點狀態與關系為0。若Hi為網絡中的節點,對于P(Hi=0|Πi=1)和P(Hi=1|Πi=1)兩者符合概率的公理約束,對節點的危險性預測僅對P(Hi=1|Πi=1)進行分析即可。

通常攻擊者為達到攻擊目的,一般需要通過對多個漏洞的連續利用,用已占有資源節點作為跳板,去占有其他資源,直到完成攻擊目的形成攻擊路徑。因此,路徑可達概率通常作為路徑評估的標準,路徑可達概率θPath計算方法如下所示:

θPath=P(H1)×P(H2|Π2)×…×P(Hi|Πi)×…×P(Hn|Πn)

(21)

4.2 案例驗證分析

由于網絡安全領域缺乏驗證數據集,因此為了驗證本文所提的安全評估方法,本文構建以歸一化通用漏洞評分系統(common vulnerability scoring system, CVSS)[32]的評分為BN參數的仿真平臺,來進行閉環驗證。CVSS是權威的漏洞嚴重性評估系統,作為行業公開的評分標準,為網絡安全評估的量化提供了一個開放的計算框架。CVSS將漏洞被利用的嚴重程度歸于一個[0,10]數值區間,分值越高說明漏洞的危險程度越大。圖3是一個BN攻擊圖,圖中除H1和H17之外,每個節點代表網絡中的漏洞,H1為攻擊者的攻擊發起節點,H17為攻擊者最終要到達的目標節點。表11為圖3中除初始節點和目標節點外,節點的漏洞信息表。表11中包括通用漏洞披露(common vulnerabilities & exposures, CVE) 標號、CVSS評分歸一化近似約束。假設漏洞對于攻擊者為可用狀態時標記為1,不可用為0。P(H6=1|Π6=1)表示節點H6被“攻占”成功的概率,其中Π6=1表示節點H6的前序節點已經被“占領”,即H2或H3關系為1。

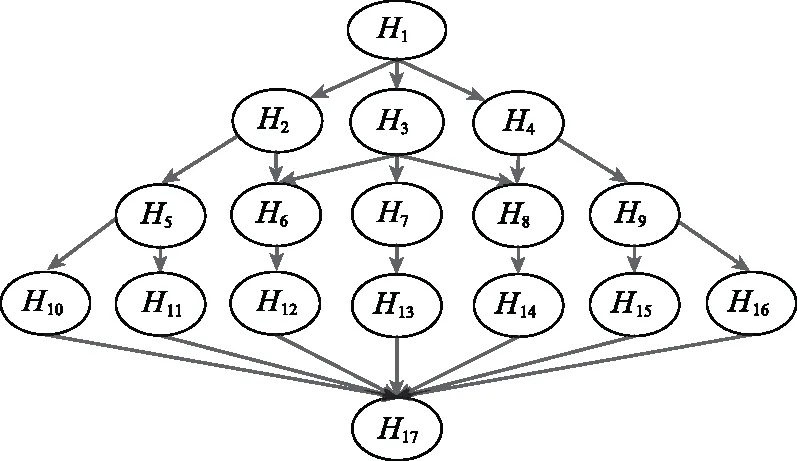
圖3 BN攻擊圖Fig.3 BN attack diagram

表11 漏洞信息及約束

通過FMAP算法分別進行4個樣本量下的學習,P(Hi=1|Πi=1)結果如表12和表13所示。

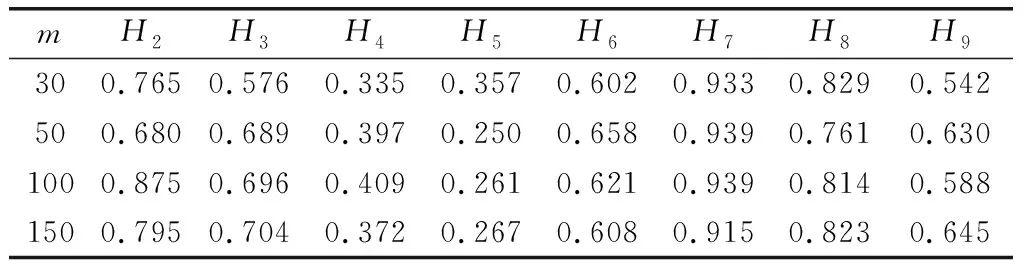
表12 節點H2～H9參數學習結果

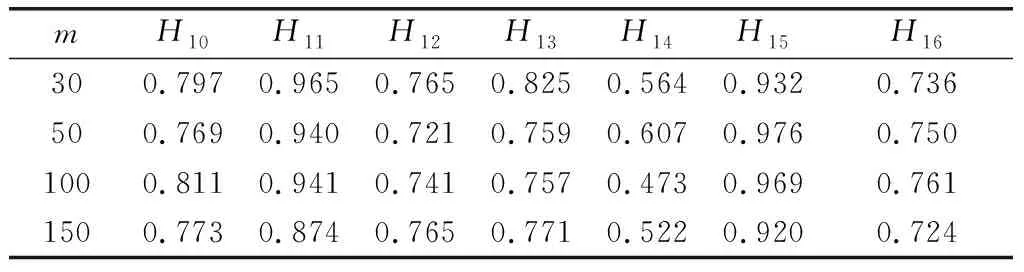
表13 節點H10～H16參數學習結果

由于網絡中漏洞很多,在有限時間內,安全管理員難以完全處理每一個漏洞。因此,如果能有效地預測出高危節點,即P(Hi=1|Πi=1)最大的節點,將會為網絡安全管理員提供有益的幫助。本文將各樣本量下的P(Hi=1|Πi=1)學習結果進行排序，并和CVSS評分的前10節點對比,來驗證學習結果的有效性。由表12和表13可以看出,在樣本量為30時,預測正確率為90%,其他樣本量下為100%。

路徑可達概率是網絡攻擊預測重要參考指標,本文假設H17為網絡中目標節點,攻擊者可選擇通過網絡中不同的路徑進行攻擊從而到達目標節點,實現攻擊目的。圖4所示為9條路徑分別在不同樣本量下參數計算出的路徑可達概率。可以看出,4個樣本量評估出得分最高的5條路徑結果和CVSS一致,在30樣本量下的預測成功率為80%,而其他的樣本量下完全一致,同時隨著樣本量的提高,評估結果和CVSS更加相近。

圖4 網絡路徑可達概率Fig.4 Network path accessibility probability

5 結 論

本文提出一種基于模糊先驗約束的BN參數學習方法,來解決小樣本下BN參數學習問題。將隸屬度函數和實際樣本量引入到構造超參的構建中,從而平衡參數學習過程中的過擬合與欠擬合問題。實驗證明,本文算法可以有效地提高參數學習結果的精度,并擁有杰出的魯棒性。同時,將本文方法引入到網絡安全評估中,將CVSS評分作為專家先驗,利用漏洞編號遷移樣本進行參數學習。本文算法雖然可以有效地提高小樣本下參數學習的精度,但本文提出的模糊超參構建過程相對復雜,需要消耗更多的時間。