基于LMD-WSVD的半球諧振陀螺混合去噪方法
常龍康, 魏健雄, 于 飛,*, 張國昌, 高 偉, 郝 強
(1. 哈爾濱工業大學儀器科學與工程學院, 黑龍江 哈爾濱 150001; 2. 哈爾濱工程大學煙臺研究院, 山東 煙臺 264000; 3. 中國艦船研究院, 北京 100101)
0 引 言
半球諧振陀螺(hemispherical resonant gyroscope, HRG)[1-2]是基于哥氏振動的新型固體振動陀螺,它具有無轉子、高精度、高可靠、抗輻射的特點,尤其是壽命長,可達15年,這是其他類型的陀螺所無法比擬的。但是在實際應用過程中,HRG易受到外界噪聲的影響[3],使得陀螺輸出信號中包含了大量的噪聲,這部分是無用的,而且其降噪性能的好壞對慣導精度起著重要的作用,因此必須對采集信號進行有效地去噪處理。
當信號是平穩的且其頻譜與噪聲不重疊時,通常采用傅里葉變換的方式進行去噪,但是陀螺儀的輸出信號通常是非平穩非隨機性的信號,對于此,有很多學者進行了大量的研究[4-5],例如:韓穎[6]采用時間序列分析法的卡爾曼濾波算法對微機電系統(micro-electro-mechanical system, MEMS)陀螺儀進行降噪處理,通過Allany方差分析證明了此方法的有效性。亓洪濤[7]提出使用變階數的最小均方(least mean square, LMS)算法來抑制光纖陀螺儀的輸出噪聲,并使用真實信號證明了此方法能夠提高系統的測量精度。Ding等[8]提出了一種優化自回歸移動平均模型的方法來抑制MEMS陀螺中的隨機噪聲。在文獻[9]中,使用自適應奇異值分解(singular value decomposition, SVD)對局放信號進行降噪,并通過對仿真和實測的局放信號進行處理,證明了其優越效果。
以上單一濾波器在處理噪聲中均有較好的效果,但各自存在一些不足,為了彌補單一濾波器的缺陷,很多學者提出了兩級濾波器來抑制陀螺的輸出噪聲。例如:胡佳等[10]提出一種改進LMS算法結合移動平均濾波的降噪方法來減少MEMS陀螺輸出信號中的噪聲分量,并通過Allan方差來辨識相關參數,從而證明了該兩級濾波器的優越性。吳佳慧等[11]通過將卡爾曼和小波相結合的方式來自適應去除MEMS陀螺中的噪聲,實驗證明了該方法能有效地提升陀螺的測量精度。本文將小波變換(wavelet transform, WT)和SVD進行級聯(WSVD),構成兩級濾波器進行降噪處理,相較于其他的算法能更好地抑制陀螺的輸出噪聲。
近年來,經驗模態分解(empirical mode decomposition, EMD)[12-13]方法被廣泛使用,因為EMD不需要任何信號的先驗知識,可以直接把原始信號分解為不同頻率的分量,避免了對所有的信號進行處理,有效地提高了精度,減少了計算量。趙昱宇等[14]采用傳統低通濾波(low-pass filter, LPF)方法對信號進行預處理以抑制高頻周期噪聲,然后應用EMD對LPF預處理的MEMS陀螺信號進行分解降噪,并分別應用于標準測試信號和實測信號來證明此方法的有效性。戴邵武等[15]采用EMD對光纖陀螺含噪信號進行分解,然后對混合模態項進行小波分析去噪,但是EMD存在模態混疊和端點效應,于是很多集合EMD[16-17]、區間EMD[18]、完備集合EMD[19]、自適應噪聲完備集合EMD (complete ensemble EMD with adaptive noise, CEEMDAN)[20]等EMD的改進方法涌現了出來,文獻[21]對信號進行CEEMDAN分解,再使用 Savitzky-Golay 算法進行處理,并與EMD降噪方法相比,證明了該算法的有效性。文獻[22]將CEEMDAN方法與提升WT技術相結合用于光纖陀螺的去噪,提高了其計算效率和濾波精度。本文提出了一種局部均值分解(local mean decomposition, LMD)方法,它具有更強的信號分解能力與時頻特征分析能力,能有效解決EMD過包絡、欠包絡等問題。
然而,在對信號進行去噪預處理時,首先需完成信號的模態分解,隨后需判斷噪聲分量與有效分量間的界限,因此本文采用排列熵(permutation entropy, PE)來判斷經過LMD分解后模態的時間復雜度,從而有效地區分信號分量和噪聲分量。
1 陀螺誤差分析
在實際多變的導航情景下,由于陀螺的誤差,在積分過程中會造成姿態的累計誤差,且陀螺的零偏誤差對姿態的影響最大[23],因此對陀螺的誤差進行分析建模和補償至關重要。
陀螺儀的誤差又可分為確定性誤差和隨機性誤差。確定性誤差中標度因數、安裝誤差占主要影響,這兩種誤差可由實驗室高精度轉臺通過位置實驗、速率實驗進行標定[24-25],計算出參數后建模并予以補償,但因為這種消除誤差的方式涉及不同轉臺的性能和陀螺自身的結構,所以本文暫先不考慮。
隨機性誤差是由于陀螺的使用環境、外界噪聲等引起的無規律的誤差,具有很大的隨機性和弱非線性,不能通過簡單的標定補償,目前常用方法是通過自相關函數、功率譜分析[26]和Allan方差[27]等方法進行參數辨識,本文采用Allan方差進行辨識參數,其參數主要有量化噪聲、角度隨機游走、速率隨機游走、零偏不穩定性、速率斜坡五部分,其中,角度隨機游走和零偏不穩定性是影響陀螺儀精度的主要因素,其數學表達式如下:
角度隨機游走數學表達式為
(1)
式中:N為角度隨機游走系數;τ為取樣時間間隔。
零偏不穩定性的數學表達式為
(2)
式中:B為零偏不穩定性系數。
通過分析隨機漂移誤差的產生原因及過程,可以建立隨機誤差模型,并采取有效的方法進行補償。本文后續的算法以航海用HRG應用為背景,主要針對HRG的隨機性誤差的濾波方法進行詳細的研究,通過實驗測試HRG的真實數據,并通過Allan方差分析對濾波后的效果進行評價,證明了本文所提出的LMD-WSVD算法的有效性和優越性。
2 理論基礎
2.1 LMD
LMD方法是一種新的自適應非平穩信號的分析處理方法,不同于EMD,它能夠自適應地將原始信號分解為若干個乘積函數(product function,PF)與1個殘余分量之和,具體流程如圖1所示。其分解過程如下:

圖1 LMD方法的流程圖Fig.1 Flow chart of the LMD method
步驟1確定原信號X(t)的局部極值點,計算相鄰兩個極值點的平均值ai以及包絡估計值bi:
(3)
式中:ni為原始信號X(t)的局部極值點。
步驟2將所有的局部均值ai和局部包絡bi進行平滑處理,就得到了局部均值函數a11(t)和局部包絡估計函數b11(t),然后用原始信號減去a11(t),得到零均值信號c11(t),如下所示:
c11(t)=x(t)-a11(t)
(4)
步驟3對c11(t)進行解調,通過對c11(t)除以b11(t)就可以得到調制函數d11(t):
(5)
步驟4重復上述步驟1~步驟2就可以通過設置的迭代方法獲得a1k(t),m1k(t),從而計算出純調頻函數h1k(t)的值,其具體步驟如下:
(6)
步驟5將上述迭代所獲得的全部局部包絡估計函數進行乘法運算就可以得到包絡信號b1(t),再乘以h11(t),得到第一個乘積函數PF1,具體如下:
(7)
PF1=b1(t)d11(t)
(8)
步驟6將步驟5中所得的PF1從中分離出來,得到u1(t),將u1(t)替代x(t)作為新的原始信號重復步驟1~步驟6,循環k次,直到u1(t)成為單調函數為止,具體步驟如下:
(9)
通過以上計算將x(t)分解為k個PF和一個單調信號uk(t)之和,即
(10)
2.2 PE
PE[28]是一種檢測動力學突變和時間序列隨機性的方法,能夠定量評估信號序列中含有的隨機噪聲。算法步驟如下:
步驟1對一組長度為N的時間序列X進行相空間重構,得到矩陣Y為

(11)
式中:m為嵌入維數;t為延遲時間;K=N-(m-1)t。
步驟2將每一個重構分量按照升序重新排列,得到向量中各元素位置的列索引構成一組符號序列。
S(l)={j1,j2,…,jm},l=1,2,…,K
(12)
步驟3計算每一種符號序列出現的次數除以m!種不同的符號序列出現的總次數作為該重構分量的概率:{P1,P2,…,PK}
步驟4計算時間序列X的PE,公式為
(13)
步驟5PE的最大值為ln(d!),將PE值進行歸一化處理,即
(14)
PE值的大小表示時間序列X的隨機程度:熵值越小,說明時間序列越規則;反之,熵值越大,則時間序列越隨機。
2.3 WSVD
2.3.1 WT
WT[29-30]是較為常用的信號的多尺度分析方法,它是針對傅里葉變換的不足而發展起來的,其具有多分辨率的特性,對于一維離散信號f(t),其WT可表示為

(15)
(16)
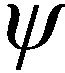
2.3.2 SVD
SVD[31]是線性代數中的經典問題,在一維的信號去噪中得到廣泛應用。方法的流程如下:
步驟1對采集到的長度為N的一維信號X(t)構造Hankel矩陣:
(17)
步驟2對MI進行SVD:
M1=UΣVT
(18)
式中:U∈R(N-n)×(N-n)是正交矩陣;V∈Rn×n是正交矩陣;Σ是(N-n)×(N-n)維非負對角陣。
步驟3對特征值進行排序,將小于所有特征值的均值的特征值分量設于0。
步驟4重構得到最終的去噪后的信號。
3 混合去噪方法
針對HRG輸出信號的特點,本文提出了一種新的混合去噪算法LMD-WSVD,如圖2所示。

圖2 LMD-WSVD方法的總體流程圖Fig.2 Overall flow chart of the LMD-WSVD method
算法步驟如下所示:
步驟1分解。將HRG的輸出信號通過LMD算法分解為若干個PF模態。
步驟2劃分。計算出每個PF分量的PE值。根據PE劃分準則,將模態分量分為低頻有用分量、混合分量兩類,并將它們重構,以便后續的處理。
步驟3分別處理。低頻有用信號中全部為有效信號,將其保留;混合分量由真實信號和噪聲構成,噪聲是無用的,需要去除,本文將WT和SVD構成二級濾波器,即WSVD方法,對混合分量進行降噪處理。
步驟4重構。將低頻有用分量和濾波后的混合分量重構,得到最終去噪后的信號。
通過上述混合去噪方法LMD-WSVD處理得到的HRG輸出數據,噪聲能夠得到很好地抑制,極大地提高了測量精度。
4 實驗測試與方法對比
4.1 實測實驗
為了驗證本文所提出的算法的有效性,開展了HRG的靜態實驗。首先搭建靜態試驗環境,利用實驗室的HRG,將其固定安裝于試驗室大理石隔震臺上,設備圖如圖3所示,通過數據總線連接將HRG供電,并通過數據線連接至計算機中,然后通過采數軟件記錄陀螺的輸出信號,采樣頻率為250 Hz。圖4所示為靜態實驗下的HRG的靜態數據。

圖3 實驗數據采集設備圖Fig.3 Experimental data acquisition equipment diagram
4.2 方法驗證
將得到的HRG數據進行LMD,得到5個PF分量,如圖5所示。從圖中我們可以看出,信號和噪聲混合在了一起,對每個分量都進行處理,會有很大的計算量且會使信號失真,為了有效地區分有用信號模態和噪聲信號模態,本文采用PE準則來計算各個模態的熵值的大小,根據PE值的大小將它們分為兩個分量:低頻有用分量和混合分量,將它們分類后的模態進行重構,以便后續的處理,如圖6 所示。

圖5 LMD分解結果Fig.5 Decomposition results of LMD

圖6 PE的劃分結果Fig.6 Classification results of PE
將上述分類好后的兩類根據信號的特性采用不同的策略繼續處理:對于低頻有用分量,其包含了大量的信號,直接保留即可;對于混合分量,其包含了有用信號和噪聲分量,本文采用WSVD方法,將WT和SVD方法構成二級濾波器,對混合分量進行去噪處理,最后將兩個類型分量進行重構,得到最后的信號,如圖7所示。從圖7我們可以清晰地看出,相比較原始信號,LMD-WSVD方法能夠很好地抑制HRG輸出信號的噪聲,提高了陀螺的測量精度。
4.3 方法對比
為了驗證此方法的優越性,將此方法與EMD-LPF和EMD-LMS相對比,對比結果如圖8所示,從圖8我們可以看出,本文所提出的方法有較佳的去噪能力。

圖7 原始信號和去噪后信號的比較Fig.7 Comparison of the original and denoised signal

圖8 不同方法之間的對比Fig.8 Comparison of different methods
為了定性地分析所提出的LMD-WSVD方法的有效性和優越性,本文采用Allan方差[32]來驗證,結果如圖9和表1所示。圖9和表1表明,濾波后零偏穩定性有所下降,角度隨機游走減小了一個到兩個量級,其中,相比原始信號,零偏穩定性降低了60.3%,角度隨機游走降低了99.9%,說明了LMD-WSVD對HRG的降噪效果最為明顯。

圖9 不同方法的Allan方差對比Fig.9 Comparison of Allan variance of different methods

表1 Allan方差分析結果
5 結 論
本文提出了一種LMD結合WSVD的HRG去噪方法:通過LMD對HRG信號進行分解后,利用PE準則計算PF分量的PE值,根據PE值將分量劃分為兩類:低頻有用分量和混合分量,并分別處理:保留低頻有用信號,將WT和SVD進行級聯,構成兩級濾波器對混合分量降噪處理,最后,將二者重構,得到最終去噪后的信號。在實測實驗中,將原始信號和EMD-LPF、EMD-LMS、本文所提的方法進行了比較。結果表明,相比原始信號,LMD-WSVD方法能夠有效地減少HRG中的輸出噪聲,提高其測量精度,其中角度隨機游走降低了99.9%,零偏穩定性降低了60.3%;同時相比其他方法,LMD-WSVD去噪能力也更顯著。

