基于領域劃分的小學數學推理意識發展

殷如意　張明華　凌靜

摘 要 推理是數學邏輯思維的基本形式，是小學數學核心素養要素之一。基于小學數學領域特點，分別從四個領域內容出發，探討代數推理、空間推理、數據推理、綜合推理的內涵，分析其在小學數學教材中的存在，思考在數與運算中融合代數推理、在圖形認識與運動中生成空間推理、在數據整理分析中體驗數據推理、在綜合實踐中運用綜合推理的具體措施。

關? 鍵? 詞 數學推理 代數推理 空間推理 數據推理 綜合推理

引用格式 殷如意，張明華，凌靜.基于領域劃分的小學數學推理意識發展[J].教學與管理，2023（05）：29-34.

推理是數學的特性，既是學習方式也是發展目標。縱向而言，從1950年第一份小學算術課程暫行標準[1]，到《義務教育數學課程標準（2011年版）》（以下簡稱《課標2011》），再到《義務教育數學課程標準（2022年版）》（以下簡稱《課標2022》），都強調要促進學生推理意識與推理能力的發展，《課標2011》明確指出要將推理能力的發展貫穿在整個數學學習過程中[2]，《課標2022》強調了推理意識與推理能力的整體性、階段性關系[3]。橫向而言，世界多國數學課程標準都強調了對學生推理能力發展的要求，如《澳大利亞課程標準：數學（8.4）》[4]將數學課程旨在向學生逐漸滲透數學推理的美作為其重要的課程理念。PISA2021[5]中推理是學生數學素養的構成要素。推理同樣是我國學生數學核心素養發展表現之一。

推理作為數學邏輯思維的基本形式，是從一個或幾個已有命題得出另一個新命題的過程，具體而言是個體對數學對象（如概念、性質、命題、規則等）進行邏輯思考（觀察、比較、歸納、類比等），從而推理得出結論，并通過舉證、反例等對所得結論合理性進行論證的綜合能力[6]。一般分為合情推理、演繹推理，其中合情推理是小學數學學習的核心推理方式，是個體基于現有條件、經驗、事實，通過直覺、觀察、比較等活動，采用歸納和類比等方式推斷某些結果，并對結論進行驗證的一種思維過程；演繹推理則是從一般事實出發（法則、性質、定理等）進行個別論證的過程。《課標2011》總目標中提出，學生要在觀察、猜想、證明等數學活動中，發展合情推理和演繹推理能力，第一學段目標強調能對調查過程中獲得的簡單數據進行歸類，第二學段目標注重在觀察、實驗、猜想、驗證等活動中，發展合情推理能力。《課標2022》將推理意識作為小學階段數學核心素養固定下來，強調學生對邏輯推理過程及其意義的初步感悟[7]。推理本身有利于學生觀察能力、比較能力、歸納能力、猜想能力的發展，豐富學生的數學趣味性、邏輯性過程體驗。

一、領域劃分下的數學推理

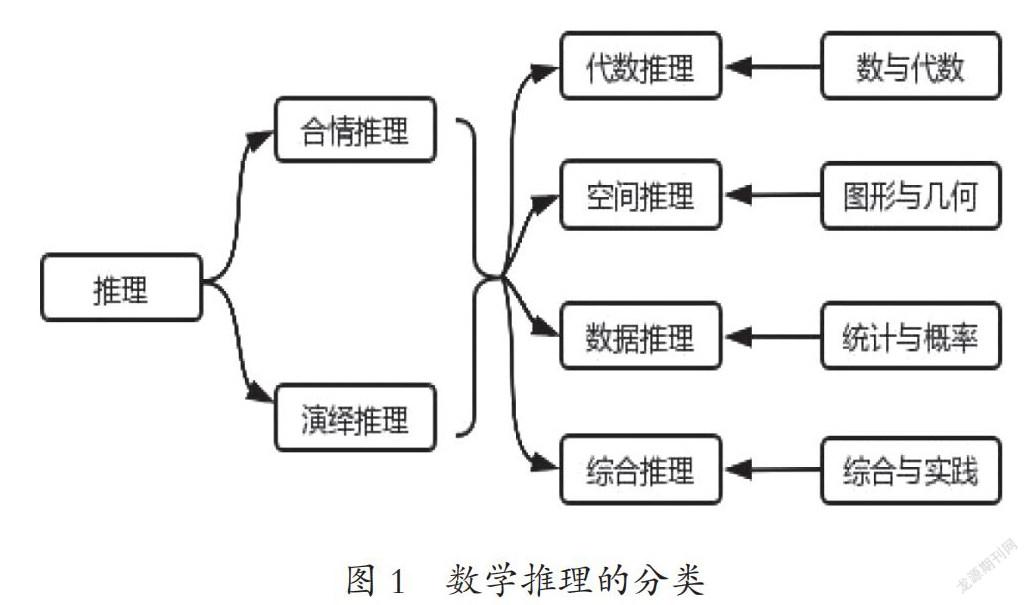
小學數學教材、教學中的推理不同于數學知識點的顯性存在，而是一種潛在性特點更突出的數學特性，在“數與代數”“圖形與幾何”“統計與概率”“綜合與實踐”四大領域以不同的形式存在，有著不同的發展要求。因此，基于小學數學不同領域的內容特點，在推理的基本內涵下，嘗試結合領域特點探討代數推理、空間推理、數據推理、綜合推理的內涵及發展策略。

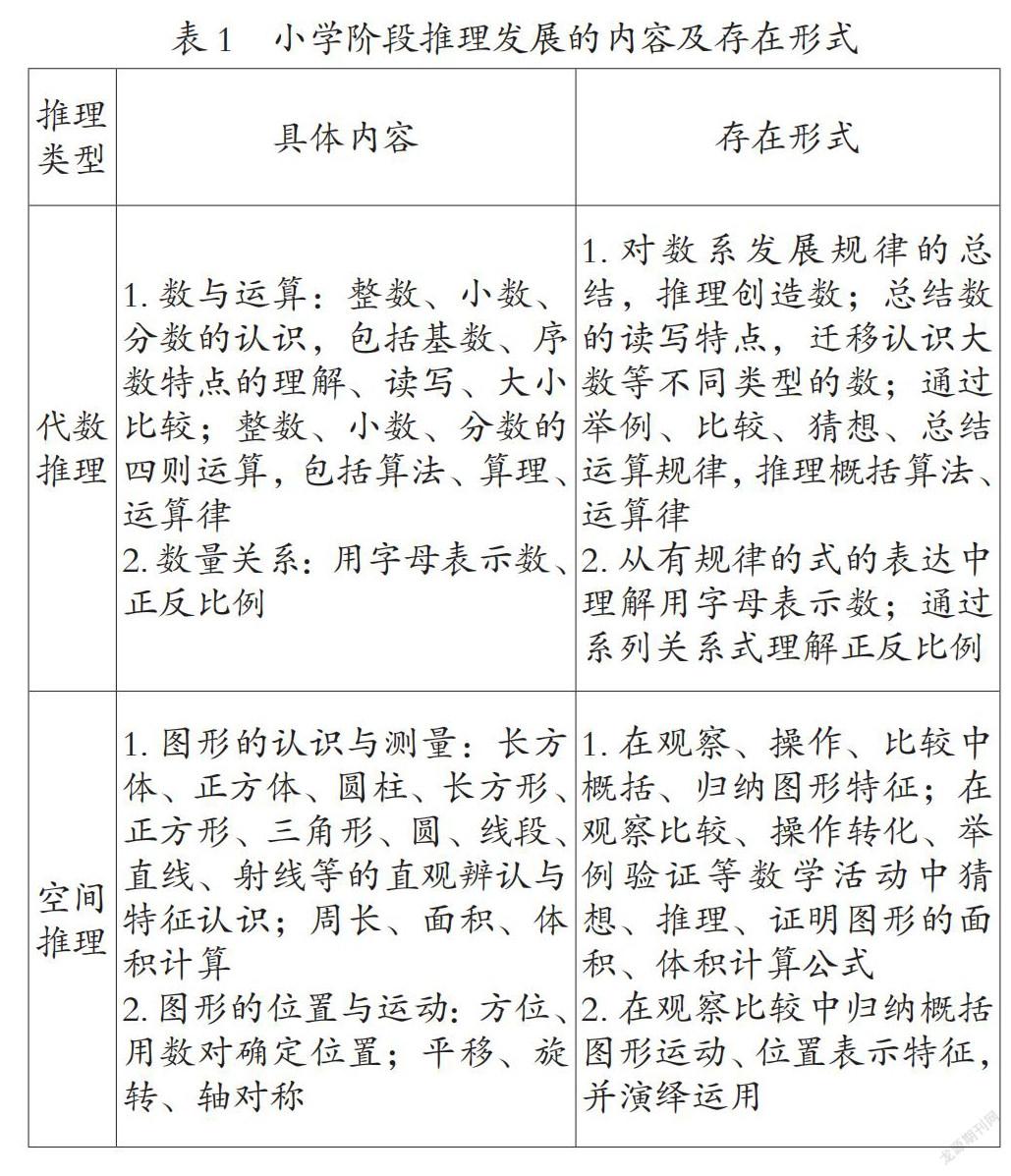
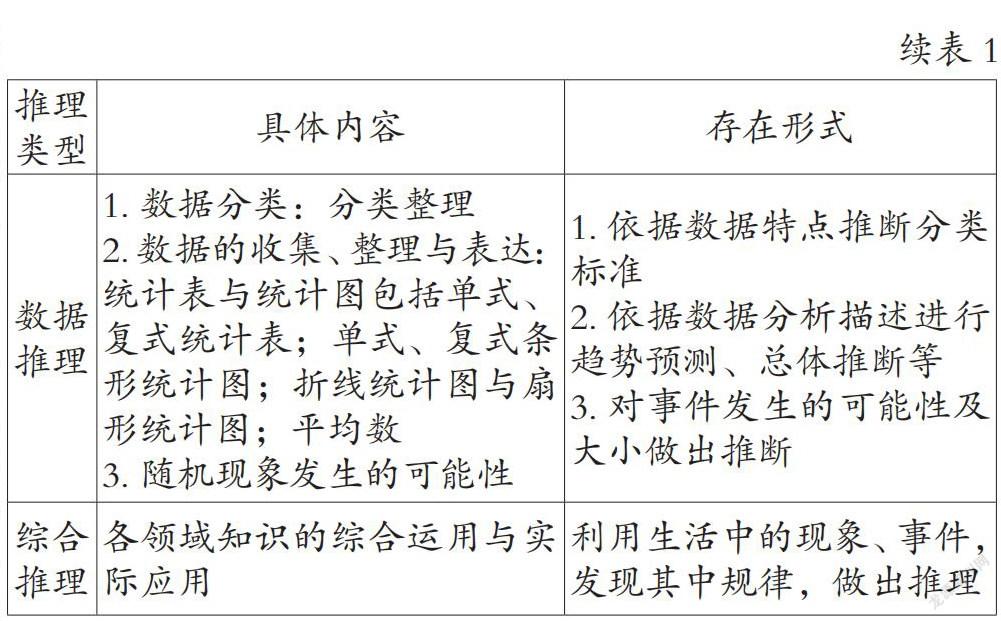
2.數量關系：用字母表示數、正反比例 1.對數系發展規律的總結，推理創造數；總結數的讀寫特點，遷移認識大數等不同類型的數；通過舉例、比較、猜想、總結運算規律，推理概括算法、運算律

2.從有規律的式的表達中理解用字母表示數；通過系列關系式理解正反比例

空間推理 1.圖形的認識與測量：長方體、正方體、圓柱、長方形、正方形、三角形、圓、線段、直線、射線等的直觀辨認與特征認識；周長、面積、體積計算

2.圖形的位置與運動：方位、用數對確定位置；平移、旋轉、軸對稱 1.在觀察、操作、比較中概括、歸納圖形特征；在觀察比較、操作轉化、舉例驗證等數學活動中猜想、推理、證明圖形的面積、體積計算公式

2.在觀察比較中歸納概括圖形運動、位置表示特征，并演繹運用

1.代數推理

“數與代數”領域的推理通常與數和運算相關，包括對數字與計算進行總結，將所得結論用有意義的符號進行表達并加以探索驗證。小學數學中的代數推理具體可表現為對數的屬性、符號意義、運算規律等的發現與概括，如奇數、偶數的特點，運算律的歸納，乘法口訣的編制等。代數推理能夠促進學生對數的不同屬性的感知、理解運算的道理，發展數感、符號意識、運算能力等。尋找（looking for）、識別（recognizing）、概括（generalizing）與運用（using）潛在的數學結構（mathematical structures）是代數推理的活動要素[8]。這利于改變記憶、模仿等機械的學習方式，啟發學生在觀察、比較、歸納中發現規律，歸納數學知識。

如“商不變的性質”，結合“6個桃分給3只小猴，60個桃分給30只小猴，600只桃分給300只小猴”的故事情境，引導學生列出：6÷3=2，60÷30=2，600÷300=2系列算式，通過觀察、比較逐步發現規律，三組算式被除數、除數都不同，但商相同，同組內被除數、除數相對于其他組總是同時擴大或縮小相同倍數，初步猜想被除數和除數同時乘或除以相同的數，商不變，通過舉例驗證，得出被除數和除數同時乘或除以相同的數（0除外），商不變。

“探索規律”是“數與代數”領域的個性化模塊，是促進學生推理意識發展的重要載體，如“有趣的乘法計算”（如圖2）。

學生通過觀察比較，發現算式本身的特點“都是兩位數乘11”，之后引導學生比較乘積與乘數，初步發現乘積的規律“積的個位與第一個乘數的個位相同，積的百位與第一個乘數的十位相同，積的十位等于第一個乘數個位與十位上數相加之和”。由此鼓勵學生猜想兩位數乘11的計算結果是否都具有這樣的規律，并舉例進行計算驗證，注意乘數個位與十位上數相加之和大于等于10的情況，從而得到結論“兩頭一拉，中間相加，滿十進一。”

2.空間推理

空間觀念發展是“圖形與幾何”領域的素養要求，強調實物與圖形之間的轉換、圖形位置關系的變換等。而空間推理指個體由空間對象或表征建造心像并進行操做，以進行空間表征間變換的認知歷程，因此空間推理是建立空間表象、發展空間觀念、增進空間想象的思維依托。小學數學教學中的空間推理可表現為個體對空間對象的表征、平移、旋轉、分類、轉換和想象等操作及心理活動。

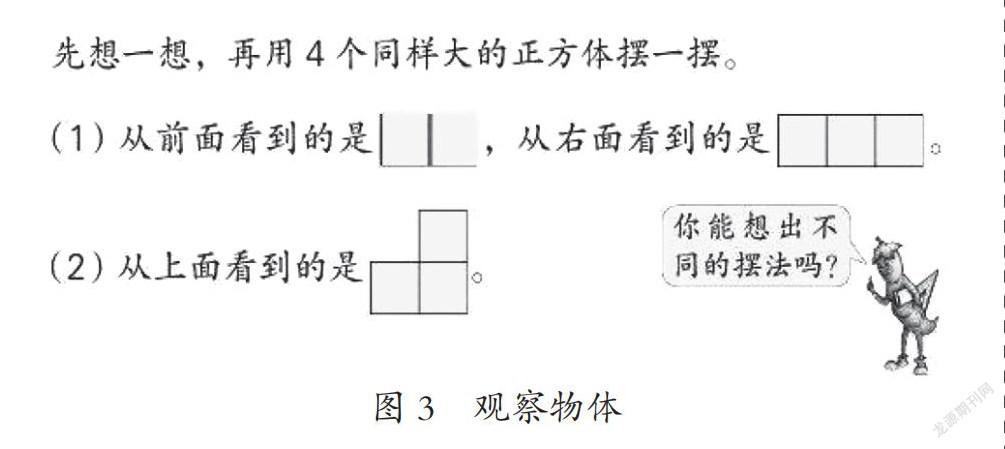
張僑平教授認為在小學階段，“三視圖”問題是培養學生空間推理能力的要點。在處理三視圖問題時需要學生空間定位（spatial orientation）、三視圖的解碼（decoding）、空間組織（spatial organization）等不同方面的能力[9]。如在“觀察物體”（如圖3）的學習中，要求學生能夠根據三視圖想象出實際圖形，即對學生三視圖解碼能力的要求，通過三視圖對立體圖形的形狀進行推理。學生通過想象自己不同的觀察角度，逐步推理、縮小、確定圖形，首先從視角1猜想、推理圖形的可能樣式，再基于視角1，從視角2進一步猜想、推理、縮小圖形的類型，之后基于視角1、視角2，從視角3推理、確定最終圖形。

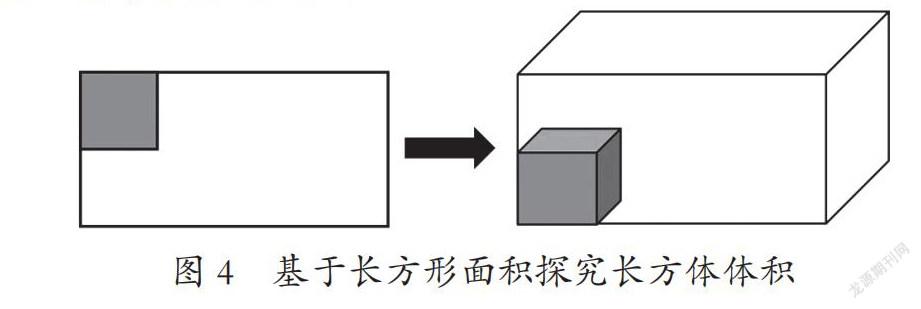
“圖形與幾何”領域的空間推理，既表現為內容、結果的推理，也可表現為方法推理，如基于長方形面積探究長方體體積。一方面可通過對長方形、長方體關系及相似性的比較，大膽推測因為s=ab，所以v=abh，對長方體體積做出結果性類比推理；另一方面，同樣基于長方形、長方體相似性的比較，通過擺小正方形探索長方形面積的思路，推測用擺小正方體探索長方體體積，對長方體體積做出探究方法的類比推理（如圖4）。類似的推理還存在于長方形面積到平行四邊形面積，平行四邊形面積到三角形面積，再到梯形面積的方法推理。

3.數據推理

數據意識發展是“統計與概率”領域的素養表現，包括理解收集數據的必要性，通過分析做出判斷，體會數據中蘊涵著的信息，了解數據分析方法多樣化，感受數據隨機性等。通過統計數據，利用數據分析問題，做出大膽預測，進行推理是統計教學的重要意義。在小學數學教學中數據推理可表現為基于數據的收集、分析，總結數據規律，做出推斷與預測，并應用于生產生活。

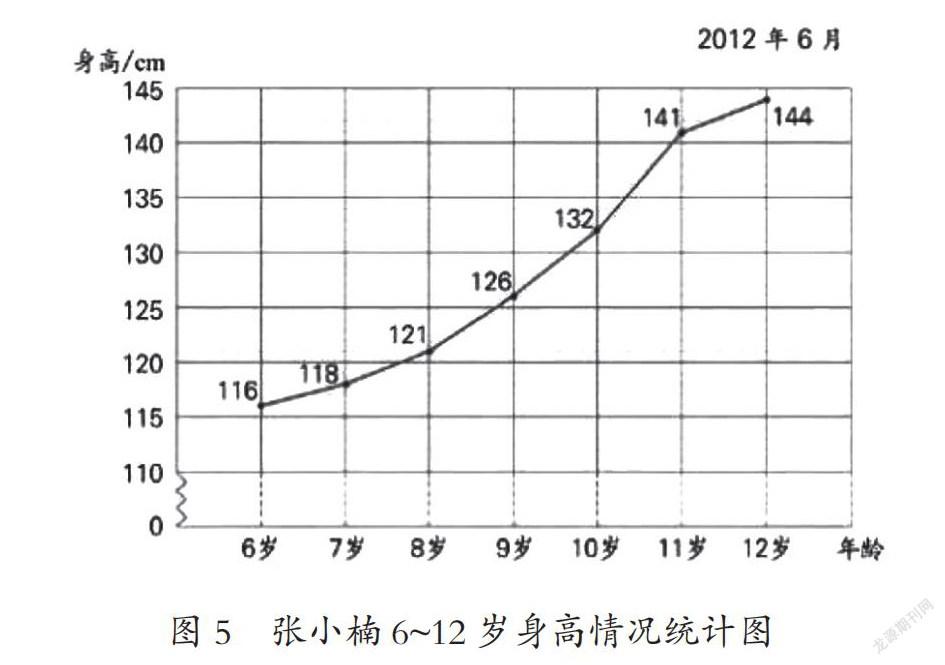
數據時代，數據的收集與整理是進行問題分析、趨勢推斷、措施抉擇的基本依據，數據意識強調學生對數據的敏感性，能夠從數據中獲取信息、應用數據，并依據數據做出推斷。折線統計圖的特點之一是能夠較好地通過數據反映變化趨勢，因此也是促進學生推理意識發展的直接載體。不同版本小學數學教材中都結合具體情境，利用折線統計圖發展學生推理意識與推理能力，如蘇教版數學教材基于張小楠6～12歲的身高變化可對其13歲的身高做出推斷（如圖5）。

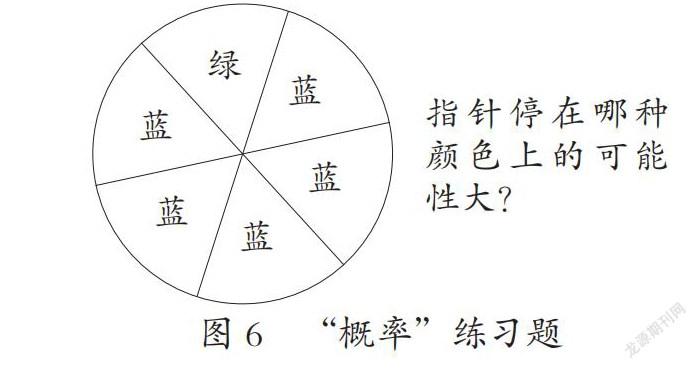
“概率”內容常用于推斷，有利于學生推理意識的建立及推理運用，概率分析方法一般分為兩種：一種是依據所有可能的結果去判斷某種結果出現的可能性；一種是通過重復試驗，由事件的頻率估計概率[10]。如圖6，一種方法可以列舉出有6種結果，其中藍色5種，綠色1種，所以停在藍色上的可能性大；另一種方法可以組織各個小組進行20次的轉動活動，結果停在藍色中的次數更多，也有可能一樣多（較少），或停在綠色區域次數多（偶發）。由此啟發學生對下一次所停區域進行預測，引導學生學會依據結果進行合理預測，發展合情推理意識。

4.綜合推理

綜合推理也可稱為生活推理或實踐推理，“綜合與實踐”領域是對其他三個領域所學知識技能以及個體經驗積累的綜合運用，其目的在于促進學生應用意識及能力的發展。因此，小學數學中的綜合推理可理解為數學推理各種形式的綜合運用，以及數學推理在實際生活中的實踐應用。

如蘇教版《數學》四年級下冊中“綜合與實踐”領域的“數字與信息”，可利用家庭成員、同一地區成員身份證信息的異同點，引導學生推理發現身份證前6位數字、7-14位數字編碼的規律，理解地址碼和出生日期碼，利用男、女同學身份證信息推理身份證第17位數的編碼規律——男性為奇數，女性為偶數等。

推理是日常生活的一部分，推理可以培養學生將事件由局部放大到整體的意識與能力，如警察在辦理案件時，通過時間、地點等信息的疊加，對案件做出推理判斷；依據不同生物的特性類比推理，創造出可供人類使用的飛機、潛水艇等；依據所觀測到的數據對天氣變化做出預測，尤其是在夏季對降水情況做出預測，做好防御措施等。

二、基于領域特點發展數學推理

1.在數與運算中融合代數推理

《課標2022》將“數與代數”領域劃分為“數與運算”“數量關系”兩個主題。“數與運算”指整數、小數和分數的認識及其四則運算，學生需要理解掌握數的概念，理解算理、掌握算法，數本身存在有序性、規律性，教師應引導學生探索發現數的規律，發展推理意識，算法總結應建立在學生對運算規律歸納概括的基礎上，促進學生合情推理意識與能力發展。“數量關系”是指用“數”與“符號”表達“運算”及解決問題的過程，離不開“數與運算”，因此“數與代數”領域有豐富的推理素材，教師可在不同內容中滲透推理環節，促進學生推理意識的形成。

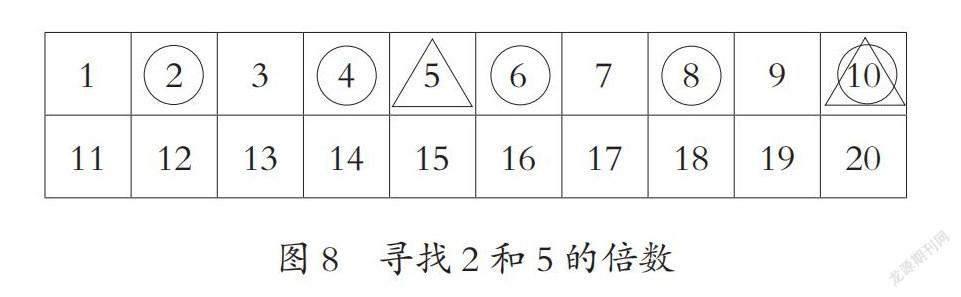
（1）創造數，歸納規律。如在“2和5的倍數”學習中，首先基于學生對倍數的學習，組織學生自主、有序地分別寫出一些2和5的倍數（通常學生會通過分別與1、2、3……各數相乘的方法有序尋找），再引導學生觀察所列出的2和5的倍數特征，發現2的倍數末尾總是2、4、6、8、0，而5的倍數末尾總是5、0，由此初步歸納推理得到2和5的倍數特征（如圖8）。基于此，鼓勵學生利用現有發現直接寫出一些2和5的倍數，再通過計算的方式驗證。如此學生通過觀察、比較、猜想、驗證的數學活動歸納推理出2和5的倍數特征，并能夠運用規律更加便捷地列舉2和5的倍數。

（2）概括算法，演繹運用。如“小數乘法”的學習，在引導學生理解算理的基礎上，啟發學生對多個算式中乘數中的小數位數與乘積中的小數位數進行比較，發現“乘數中總共有幾位小數，乘積中就有幾位小數”，并對小數乘法的算法提出猜想“小數乘法中乘數中有幾位小數，就從積的末尾數出幾位，點上小數點（注意末尾有0的情況）”，由此通過猜想舉例，計算驗證猜想，歸納出算法。

同樣，可以引導學生歸納出不同的運算律，如“乘法分配律”的學習，引導學生結合情境列出（6+4）×24或6×24+4×24，比較兩個算式的關系、異同后，可得到：（6+4）×24=6×24+4×24。并做出解釋：等號兩邊的數字相同，運算順序不同，計算結果相同；等號左邊先算了6與4的和，再與24相乘，等號右邊將6、4分別與24相乘再相加。在初步發現規律的基礎上，學生再列舉一些同類型的例子，比較歸納得到：兩個數的和與一個數相乘，可以把這兩個數分別與這個數相乘，再相加，即（a+b）c=ac+bc。且可引導學生比較發現在此算式中先算（6+4）更簡單，由此啟發學生將乘法分配律演繹運用到日常計算中，簡化計算過程。

2.在圖形認識、測量、運動中生成空間推理

《課標2022》中“圖形的認識與測量”和“圖形的位置與運動”是“圖形與幾何”領域的兩個主題。“認識與測量”中對于圖形特點的概括，以及面積、體積計算公式的推導過程，都是學生推理意識發展的重要素材，對于圖形由直觀辨認到系統認識都需經歷觀察比較、歸納總結、概括特點的認識過程，對于多邊形面積的探索同樣需要在觀察比較、舉例驗證、歸納概括的推理過程中生成面積計算公式，且平面圖形和立體圖形之間的相似性是發展類比推理的重要憑借。

（1）猜想歸納，推導公式。圖形面積計算公式的推導是發展學生空間推理意識較為顯性的素材，以“三角形面積”為例，可引導學生對方格紙中平行四邊形沿對角線分成的兩個三角形的面積大小進行觀察、比較、猜想，初步得到“平行四邊形可分成2個完全一樣的三角形”“兩個完全一樣的三角形可以拼成一個平行四邊形”“所分成的三角形的面積是平行四邊形的一半”“三角形面積等于底乘高除以二”等結論與猜想，并鼓勵學生用幾組兩兩相同的三角形進行拼搭，整理三角形的底、高、面積與所拼成的平行四邊的底、高、面積的關系，在比較歸納中得到結論。此過程能讓學生充分經歷觀察、比較、猜想、舉例、歸納、驗證等推理過程，能夠促進學生建立推理意識、發展推理能力，更能夠啟發學生對圖形間關系的思考，發展空間推理。在整個圖形面積學習中都應引導學生經歷面積公式產生的推導過程，準確把握幾種圖形之間的關系，能夠意識到長方形面積公式的基礎性、關鍵性，系統地促進學生空間推理發展。

（2）觀察比較，想象生成。如上文“三視圖”是促進學生空間觀念及空間推理發展的關鍵，小學階段學生對于拼搭圖形三視圖的判斷是促進學生空間想象和空間推理發展的基本素材，要想使學生正確想象或推斷從前面、上面、左面觀察到的圖形，在教學時應給予學生從不同角度觀察物體的機會，豐富學生觀察物體的經驗以及表象，儲備想象和推理的參照物，能夠在想象自己位置改變的同時，保持空間物體內部各部分的相對位置不變，逆向而言，能夠通過三視圖對立體物體的形狀進行推理。

3.在數據整理、分析中體驗數據推理

信息時代，“統計與概率”領域的內容設置體現了社會對個體發展的要求，在小學數學中主要包括數據分類、收集、整理與表達，以及隨機現象發生等內容。但統計類的教學不能只注重顯性的、直觀的數據解讀，而要基于數據的調查、整理，進行潛在信息的分析、推理、預見，這才是統計教學的本質，因此在實際教學中要引導學生在無序的數據中發現有序的規律，通過樣本對總體做出推斷，基于現有數據進行預測等數據描述與數據推斷活動。

（1）分析數據，推斷選擇。對數據的收集與分析的重要意義之一是為后續的決策提供判斷依據，在“折線統計圖”教學中，單式折線統計圖可以反映某個事件在某段時間內的變化趨勢，并依據數據分析對其走勢做出判斷。而復式折線統計圖則能夠反映兩種或兩種以上事件的信息，并能夠依據數據的比較分析做出推斷。如通過折線統計圖呈現一位選手近5場投籃比賽的得分情況，引導學生對其下一場比賽的得分情況做出推斷，并通過數據分析說明推斷依據；再如在復式折線統計圖中，呈現兩位選手近5場投籃比賽的得分情況，引導學生對下一場比賽誰贏的可能性大做出推斷，并說明推斷依據。

（2）體驗可能，推測概率。隨機現象在生產生活中普遍存在，而概率也常被用于商家活動，如“抽獎”，教師可在“可能性”的學習中設置模擬抽獎活動，引導學生對獲獎的可能性做出推斷，理解生活中買彩票中獎的隨機性和中大獎的低概率性。如設置一個被等分成12份的圓形轉盤，設置1份一等獎、2份二等獎、3份三等獎、6份無獎，學生分小組進行模擬抽獎活動，記錄每次中獎情況，經過多次操作后可發現，中獎或不中獎存在一定的隨機性，但中獎可能性約在左右，而中一等獎的可能性非常低。在此基礎上，進一步引導學生思考若等分成36份，同樣設置1份一等獎、2份二等獎、3份三等獎，其余無獎，中獎的可能性會發生怎樣的變化，并操作驗證。由此引導學生理解可能性及其大小，同時啟發學生正確認識買彩票等抽獎活動。

4.在綜合與實踐中運用綜合推理

“綜合與實踐”領域的內容以現實問題和跨學科實踐為主，在小學階段主要采用主題活動方式，既是對數學領域內所學知識的融合運用，也是數學與其他學科、生活實際相結合的綜合運用。因此，教學中既要利用教材內容引導學生進行推理，更要充分地結合現實生活、學生經驗，發現生活中的規律，運用數學推理于生活，用數學服務生活。

如蘇教版教材中的“數字與信息”、北師大版教材中的“編碼”都是利用身份證信息引導學生理解編碼，發展推理意識。以“編碼”一課為例，通過幫助探長破案的推理情境，引導學生對嫌疑人身份信息進行分析，在理解身份證、銀行卡編碼規律的同時，推理破案（如圖9）。基于本節課的學習，教師可引導學生思考自己的學號是否存在編碼規律，并鼓勵學生通過收集不同年級、班級、學生的學號進行比較，推測其中的編碼規律。在發現學號編碼規律的基礎上，啟發學生思考是否還有其他的學號編碼方式，能夠反映年級、班級、順序、男女等信息，提升學生的編碼能力和推理應用意識。

推理意識有助于養成條理清晰的思維習慣，提升交流的邏輯性，是推理能力發展不可或缺的思維經驗，能夠為形成嚴謹的科學研究態度和實事求是的工作作風奠定基礎。因此，小學階段推理意識的養成除了專題教學，更應該在四大領域中潛移默化地分散滲透，形成習慣。

參考文獻

[1] 課程教材研究所.20世紀中國中小學課程標準教學大綱匯編（數學卷）[M].人民教育出版社，2001：49.

[2] 中華人民共和國教育部﹒義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2011：5.

[3][7] 中華人民共和國教育部﹒義務教育數學課程標準（2022年版）[S].北京：北京師范大學出版社，2022：9.

[4] 李保臻，王亞妮，米鵬莉.中澳義務教育數學課程標準的比較研究[J].內蒙古師范大學學報：教育科學版，2021，34（02）：99-107.

[5] OECD.PISA 2021 mathematics framework [M].France：OECD Publishing，2018：8.

[6] 徐斌艷.數學學科核心能力研究[M].華東師范大學出版社，2019：68.

[8] 張僑平，邢佳立，金軒竹.小學數學教學中數學推理的理論和實踐[J].數學教育學報，2021，30（05）：1-7.

[9] 陳韻如，楊凱琳，林福來.小學高年級學生在立方體積木三視圖的推理表現[J].臺灣數學教育期刊，2018（01）：34.

[10] 朱榮武.在數據分析中培育學生統計推理能力[J].教學與管理，2020（17）：35-37.

［責任編輯：陳國慶］