瑪納斯河不同峰量組合下的融雪洪水風(fēng)險分析
何朝飛,王曉云,陳伏龍,唐 豪,龍愛華,3
(1.石河子大學(xué)水利建筑工程學(xué)院,新疆 石河子 832000; 2.中水北方勘測設(shè)計研究有限責(zé)任公司,天津 300222; 3.中國水利水電科學(xué)研究院流域水循環(huán)模擬與調(diào)控國家重點實驗室,北京 100038)
融雪洪水作為西北干旱區(qū)一種典型的自然災(zāi)害事件,嚴(yán)重危害了人們的人身財產(chǎn)安全,如何控制洪水的發(fā)生并有效降低財產(chǎn)損失是災(zāi)害風(fēng)險研究的重點。在隨機(jī)性洪水事件中,頻率分析是評估其風(fēng)險的有效手段。近年來,隨著全球氣候變化及人類活動的影響,洪水序列的隨機(jī)獨立同分布假設(shè)面臨極大的挑戰(zhàn)[1]。如果直接利用實測洪水資料進(jìn)行分布擬合會大大降低其結(jié)果的可靠性,因此必須進(jìn)行序列變異診斷,并對已經(jīng)發(fā)生變異的洪水序列進(jìn)行一致性處理[2]。
隨著水文頻率分析研究的不斷深入,非一致性頻率分析方法及基于Copula函數(shù)的多變量組合分析方法得到了很好的應(yīng)用研究。目前水文非一致性頻率分析方法主要從兩個角度進(jìn)行,一是基于水文序列還原、還現(xiàn)的間接分析方法,即將水文序列修正到過去或現(xiàn)在的狀態(tài);二是非平穩(wěn)極值序列的直接分析[3-4]。Singh等[5]針對洪水序列的非一致性問題首次提出了混合分布模型,并有效應(yīng)用于非一致性洪水序列頻率分析中。該分布模型既能避免水文時間序列修正和分解等轉(zhuǎn)化的煩瑣步驟,又能克服人工適線法帶來的較大誤差,因此得到了較為廣泛的應(yīng)用[6-9]。鄭錦濤等[10]在多種變異診斷方法的基礎(chǔ)上,對瑪納斯河年徑流量進(jìn)行了混合分布模型和條件概率分布模型的頻率分析,很好地描述了混合分布模型的擬合效果。
為解決單變量頻率分析與風(fēng)險評估方法不足以描述極端事件的失效概率和重現(xiàn)時間的問題[11-12],陳晶等[13]將Copula函數(shù)引入到水文學(xué)中,并闡述了其在構(gòu)建水文多變量聯(lián)合分布方面的相關(guān)問題;黃強等[14]在多變量分布模型的基礎(chǔ)上,提出了二次重現(xiàn)期概念,并分析探討了“且”“或”以及二次重現(xiàn)期在洪水風(fēng)險分析中的可靠性;高玉琴等[15]在G-H Copula函數(shù)的基礎(chǔ)上對比分析了洪水單變量風(fēng)險概率及二維、三維變量聯(lián)合風(fēng)險概率,發(fā)現(xiàn)它們之間存在明顯差異。但以上聯(lián)合分布研究均建立在水文序列一致的基礎(chǔ)上,缺少對于非一致性條件的必要考慮。
現(xiàn)階段對于干旱區(qū)融雪洪水峰量組合風(fēng)險規(guī)律的研究僅以單一變量為主要參考值,其結(jié)果往往較為片面,且在聯(lián)合分析中缺乏對變量間組合的風(fēng)險量化,風(fēng)險指標(biāo)過于單一,不能較全面地反映其設(shè)計水平值。因此,本文選取瑪納斯河流域出山口肯斯瓦特水文站1957—2014年逐日徑流量,并根據(jù)該站融雪型洪水一日一峰的典型特點,建立年最大洪峰和年最大1 d洪量的設(shè)計頻率分析樣本,結(jié)合序列變異診斷結(jié)果,選用不同子序列頻率分布構(gòu)建的混合分布為聯(lián)合分布模型的邊際函數(shù)。由聯(lián)合函數(shù)特性分析及數(shù)據(jù)結(jié)構(gòu)特征,將Gumbel Copula函數(shù)作為聯(lián)合函數(shù)進(jìn)行建模,并以流域500年一遇設(shè)計防洪標(biāo)準(zhǔn)為例,多角度分析組合風(fēng)險類型,以期為瑪納斯河流域防洪工程設(shè)計提供參考。
1 研究區(qū)概況
瑪納斯河發(fā)源于新疆天山北麓的依連哈比爾尕山,東西長198.7 km,南北寬260.8 km,流域總面積為24 300 km2,平均氣溫為4.7~5.7℃。流域地處中緯度歐亞大陸中心帶(85°01′E~86°32′E,43°27′N~45°21′N),天山北麓,準(zhǔn)噶爾盆地南部,具有明顯的大陸性干旱氣候特征。河流屬于冰雪融水和雨水混合補給型,平均年徑流總量約12.99億m3,其中海拔3 600 m以上終年積雪覆蓋,平均雪線高度為3 970 m,冰川面積多年維持在608.25 km2左右,占瑪納斯河徑流補給量的35.3%[16],是河流的主要補給源。本文研究對象為瑪納斯河肯斯瓦特水文站(85°57′E,43°58′N)控制流域(圖1),該水文站位于瑪納斯河出山口處,是干支流匯合后的主要控制點,控制面積為4 637 km2,它的建立為瑪納斯河流域融雪洪水觀測及預(yù)報起到了重要的作用。
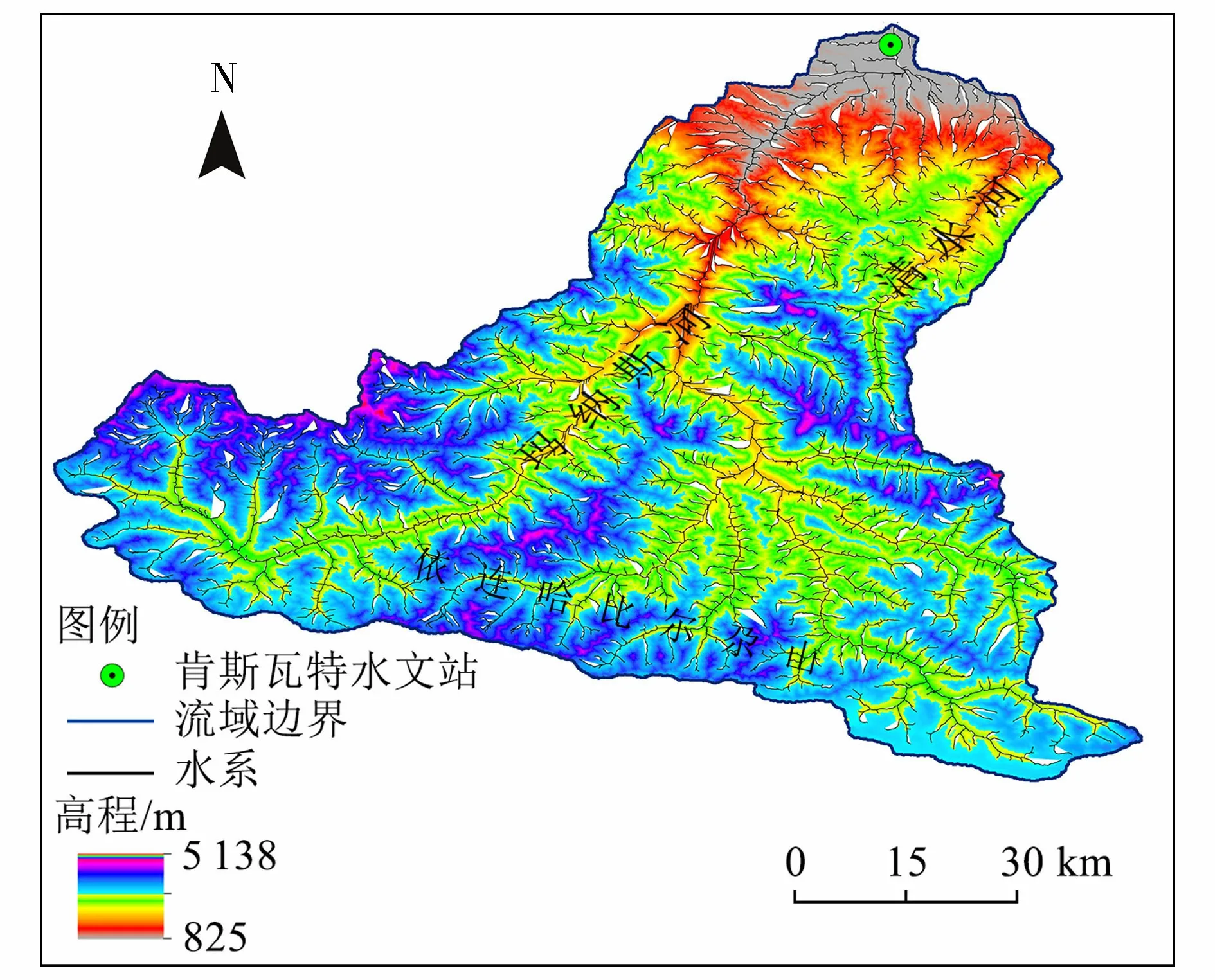
圖1 肯斯瓦特水文站控制區(qū)域
2 研究方法
2.1 累積距平法與滑動t檢驗
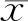
(1)
由式(1)可得n個時刻的累積距平值,其中序列突變年為絕對值最大指標(biāo)所對應(yīng)的年份。
滑動t檢驗是根據(jù)兩組樣本平均值的差異是否顯著來判斷其突變情況[18]。對于具有n個樣本量的時間序列X,基于某一基準(zhǔn)點前后兩子序列X1和X2的樣本分別為n1和n2,則統(tǒng)計量為
(2)
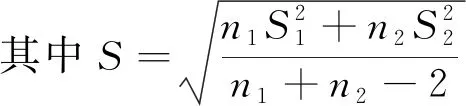
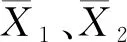
2.2 混合分布模型
混合分布模型可直接用于非一致性時間序列的頻率分析。假設(shè)該水文時間序列是由若干個一致性子分布賦予一定的權(quán)重系數(shù)累加而成:
F(x)=α1F1(x)+α2F2(x)+…+αkFk(x) (3)
式中:F1(x)、F2(x)、…、Fk(x)為各子分布的累積分布函數(shù);α1、α2、…、αk為各子分布的權(quán)重,且各權(quán)重之和為1。
為保證模型參數(shù)估計的準(zhǔn)確性,根據(jù)洪水形成機(jī)制,對洪水時間序列進(jìn)行子序列的合理劃分,使子序列的個數(shù)保持在最低限度,避免了模型的過度擬合。當(dāng)非一致性融雪洪水特征時間序列X的樣本容量為n,變異點為τ時,變異點之前的時間序列為F1,子序列服從概率密度函數(shù)為f1(x)的分布;變異點之后的時間序列為F2,子序列服從概率密度函數(shù)為f2(x)的分布;整體融雪洪水時間特征序列X服從概率密度函數(shù)為f(x)的混合分布,其表達(dá)式為
(4)
式中α′、1-α′為兩個一致性子序列的權(quán)重系數(shù)。
2.3 Copula函數(shù)及尾部相關(guān)關(guān)系
近年來,隨著水文研究工作的快速發(fā)展,多變量水文聯(lián)合分析得到了深入的研究,其中,Copula函數(shù)作為連接或耦合兩個或多個獨立變量的數(shù)學(xué)函數(shù)[19],得以普遍的應(yīng)用。將一個k元聯(lián)合分布函數(shù)用多個邊緣分布和一個Copula函數(shù)連接起來構(gòu)建多維分布,依次用來描述變量間的相關(guān)關(guān)系。本文利用二元Copula函數(shù)建立模型,其表達(dá)形式為
C(u,v)=φ-1[φ(u)+φ(v)]
(5)
式中:u、v分別為隨機(jī)變量;φ為連續(xù)、嚴(yán)格遞減的凸函數(shù),滿足φ(0)=∞和φ(1)=0;φ-1為φ的反函數(shù),且滿足φ-1(∞)=0和φ-1(0)=1。
常見的單參數(shù)Archimedean Copula函數(shù)有Clayton Copula、Frank Copula和Gumbel Copula。Clayton Copula函數(shù)對變量分布的下尾部變化十分敏感,能夠快速捕捉到其下尾的變化,Gumbel Copula函數(shù)則對變量分布的上尾部變化十分敏感,能夠快速捕捉到其上尾的變化。由于Frank Copula函數(shù)的密度函數(shù)具有對稱性,無法捕捉隨機(jī)變量間非對稱的相關(guān)關(guān)系[20],因此在洪水等極端事件中局限性較大。Archimedean族系的雙參數(shù)Copula函數(shù)可以同時刻畫上尾和下尾的相關(guān)性,因此本文采用Clayton Copula和Gumbel Copula兩種單參數(shù)Copula函數(shù)以及BB1 Copula和BB5 Copula兩種雙參數(shù)Copula函數(shù)[21]進(jìn)行分析。
2.4 組合分析計算
洪水的發(fā)生是由多種影響因素共同決定的,各變量間的相互作用也復(fù)雜多變。因此分析不同條件下的洪峰和洪量組合發(fā)生的概率,即峰量組合風(fēng)險分析是極其有必要的。本文分別選取聯(lián)合、同現(xiàn)、組合3種風(fēng)險模型[22-24],以多角度刻畫不同量級峰量的風(fēng)險概率來評價洪水設(shè)計值,其風(fēng)險概率模型見表1。

表1 風(fēng)險概率模型
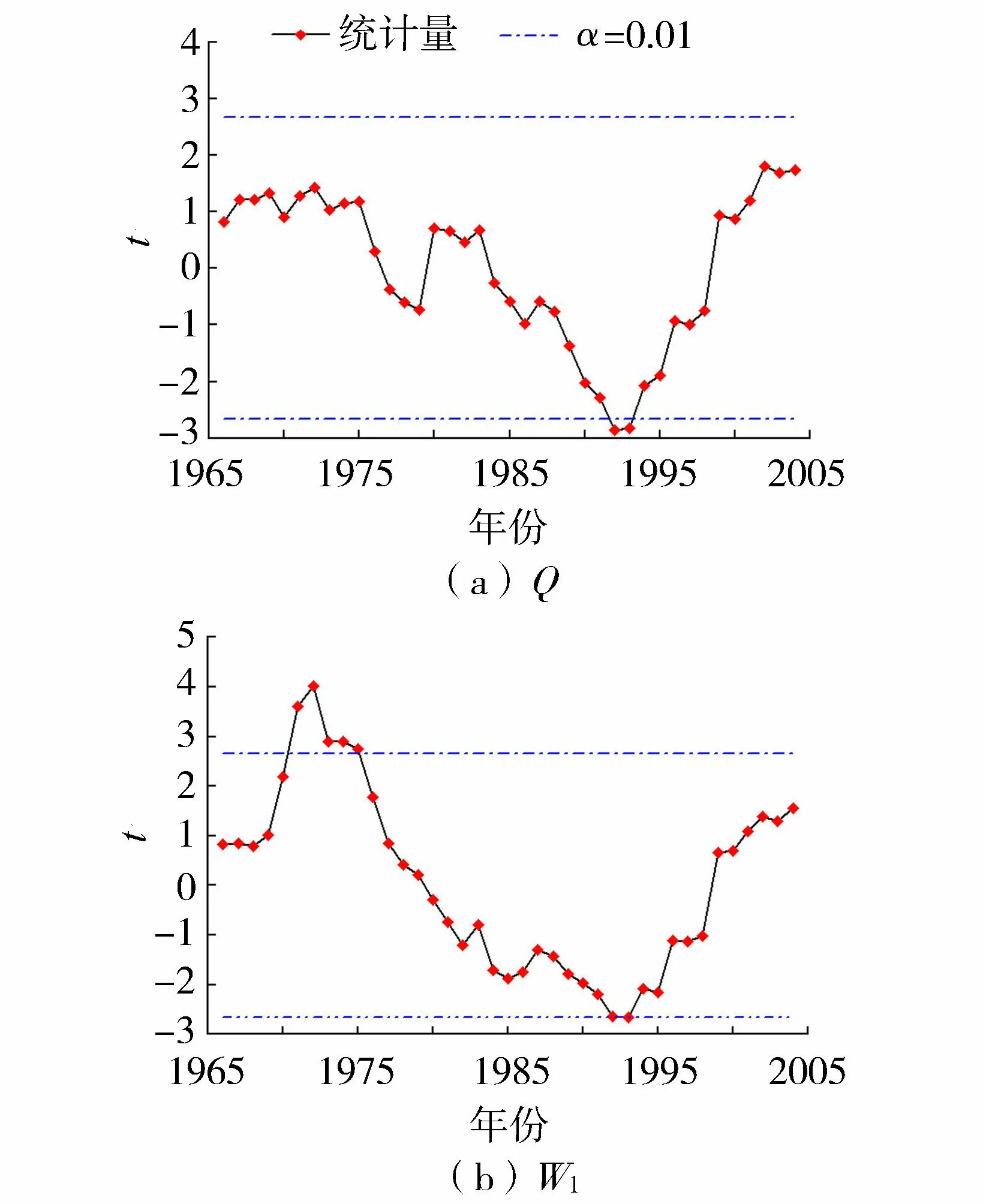
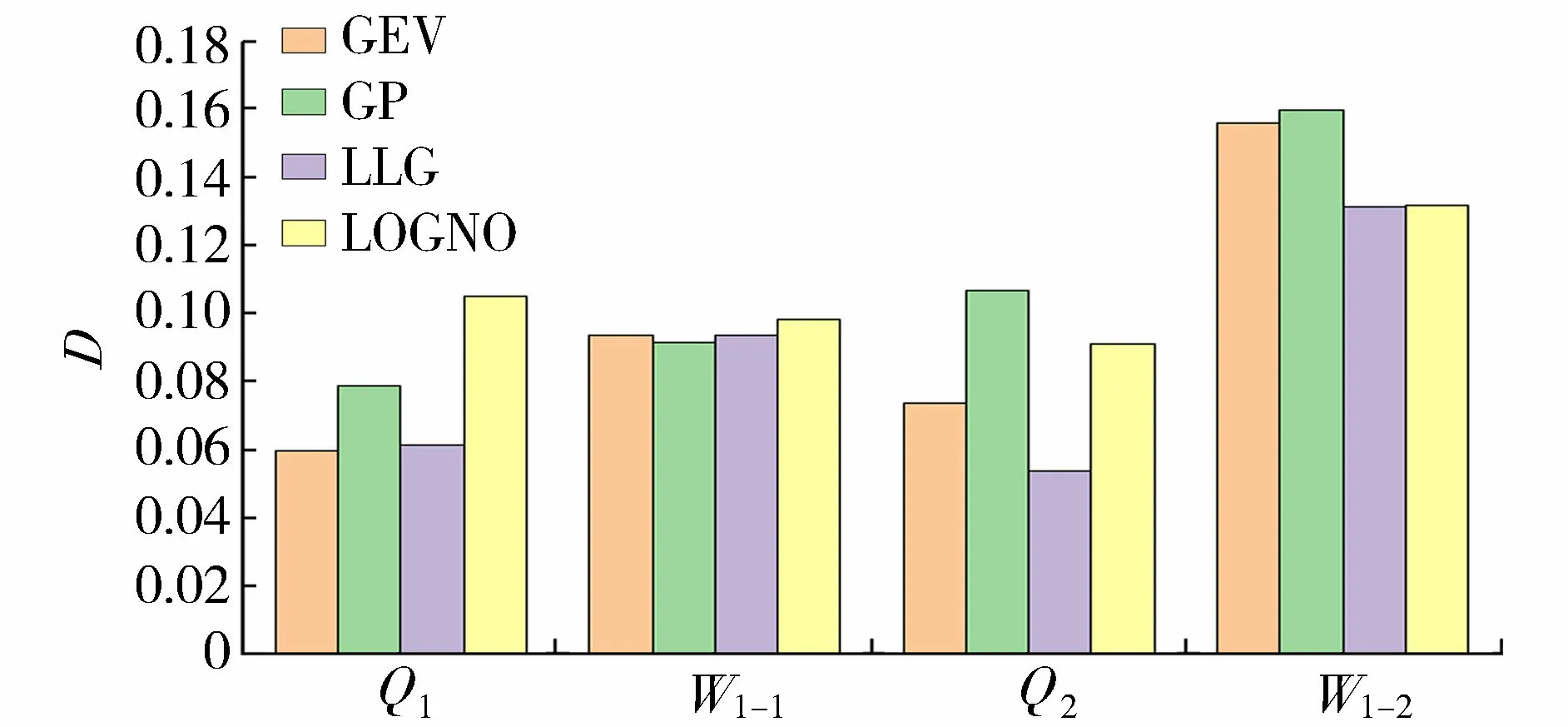
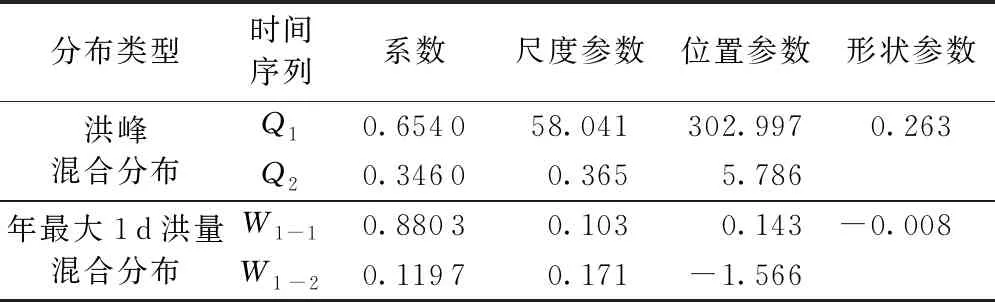
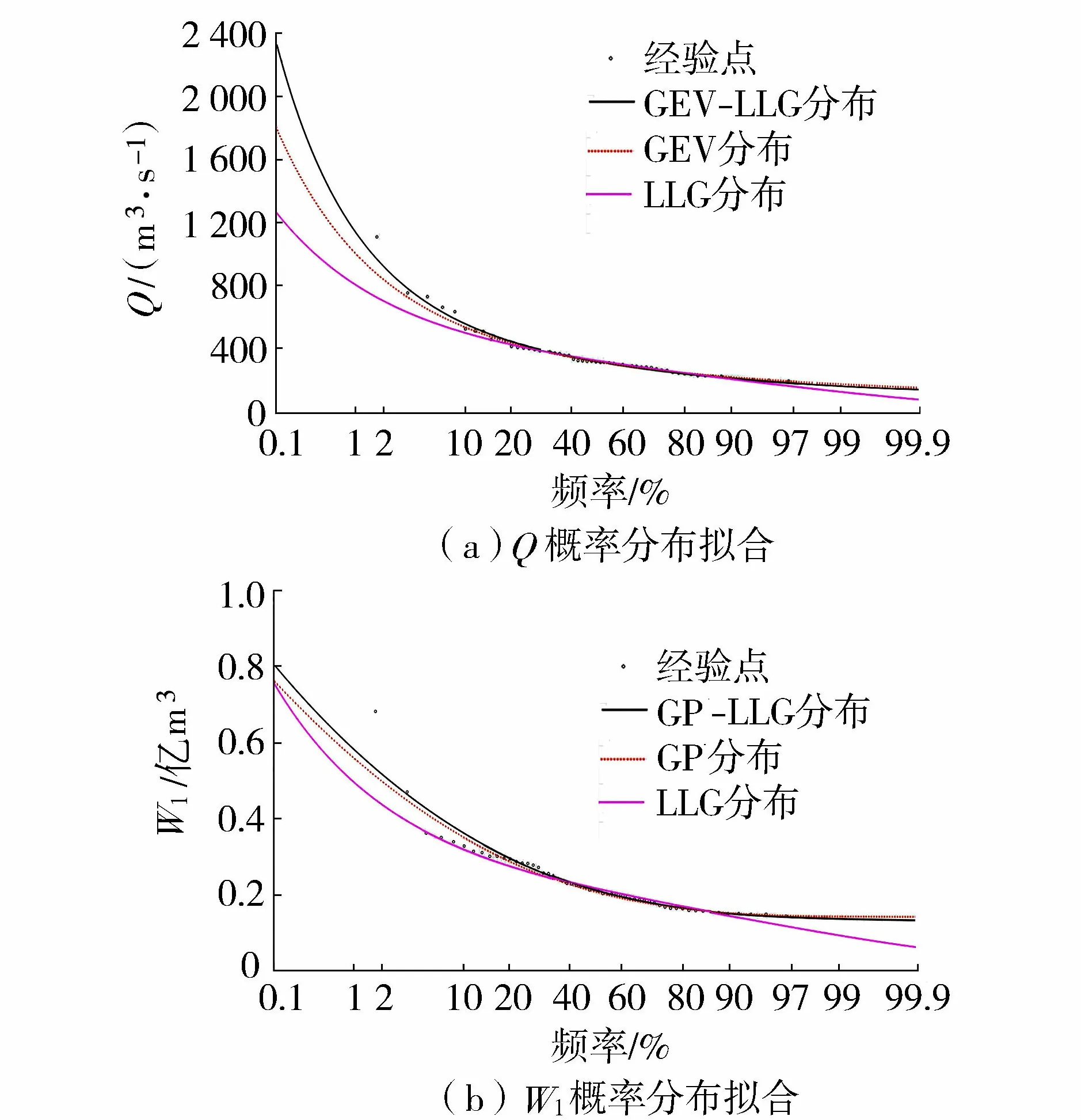
表1中Q和W1分別為年最大洪峰和年最大1 d洪量;q和w1分別為年最大洪峰和年最大1 d洪量的設(shè)計值;u=FQ(q)為年最大洪峰邊緣分布函數(shù);v=FW1(w1)為年最大1 d洪量邊緣分布函數(shù);C(u,v)=C(FQ(q),FW1(w1))為設(shè)計年最大洪峰和設(shè)計年最大1 d洪量的聯(lián)合分布函數(shù)。P(W1>w1∪Q>q)為Q與W1中至少有一個變量超過設(shè)定值的概率;P(W1>w1∩Q>q)為Q與W1兩變量同時超過設(shè)計值的概率;P(W1>w1|Q 1957—2014年瑪納斯河肯斯瓦特水文站控制流域年最大洪峰和最大1 d洪量的累積距平曲線如圖2所示,可以很直觀地看出峰量都具有先下降后上升的變化趨勢,并在1993年出現(xiàn)了較大的轉(zhuǎn)折。 圖2 峰量累積距平變化 為了進(jìn)一步確定洪水時間序列的突變年份,利用滑動t檢驗,取步長n1=n2=10,顯著性水平α=0.01,結(jié)果如圖3所示,其中年最大洪峰在1992年和1993年發(fā)生突變,年最大1 d洪量在1971—1975年、1992年和1993年發(fā)生突變。 圖3 滑動t檢驗統(tǒng)計量變化 IPCC第五次評估報告顯示,1980—2012年全球氣溫升高了0.85℃[25]。由于受冰川補給影響,從20世紀(jì)70年代至本世紀(jì)初,瑪納斯河流域冰川退縮面積為159.02 km2。在1990年前后,肯斯瓦特水文站控制流域內(nèi)下墊面變化不大。因此,氣溫變化對瑪納斯河流域洪水時間序列變化產(chǎn)生了重要影響[26-27]。綜合洪水特征分析以及滑動t檢驗,最終確定年最大洪峰序列和最大1 d洪量序列的突變年份發(fā)生在1993年,這與陳伏龍等[28]的研究結(jié)論一致,故將瑪納斯河肯斯瓦特控制流域洪水變化過程分為1957—1993年和1994—2014年兩個階段。 對于洪水變量的分布方式,本文分別就極端分布中的廣義極值(generalized extreme value,GEV)分布,廣義帕累托(generalized Pareto,GP)分布,對數(shù)邏輯斯諦克(log-logistic,LLG)分布和對數(shù)正態(tài)(log-normal,LOGNO)分布方式進(jìn)行分析比較,其中前兩個為三參數(shù)概率分布函數(shù),后兩個為兩參數(shù)概率分布函數(shù)。分布函數(shù)參數(shù)采用最大似然法進(jìn)行估計[29],并以Kolmogorov-Smirnov[30](K-S)檢驗進(jìn)行擬合優(yōu)選。圖4為各分布函數(shù)擬合優(yōu)度D,經(jīng)比較,最大洪峰1957—1993年和1994—2014年兩個子序列Q1和Q2分別采用GEV分布和LLG分布;年最大1 d洪量1957—1993年和1994—2014年兩個子序列W1-1和W1-2分別采用GP分布和LLG分布擬合。 圖4 各分布函數(shù)擬合優(yōu)度 對于混合分布模型,以頻率離差絕對值和(ABS)最小為目標(biāo)函數(shù),采用模擬退火算法[6]對參數(shù)進(jìn)行估計,其執(zhí)行策略為:在矩法初步估計的基礎(chǔ)上,給定一個最優(yōu)初始點X0開始探測整個解空間,通過擾動該解產(chǎn)生一個新解XN,按照Metropolis準(zhǔn)則判定是否接受新解,相應(yīng)地降低控制溫度,直到滿足收斂準(zhǔn)則,即沒有新解產(chǎn)生或者控制參數(shù)小到一定程度[31]。表2給出了混合分布模型的參數(shù)估計結(jié)果,根據(jù)式(3)計算洪水時間序列混合分布理論頻率。 表2 混合分布模型參數(shù)估計結(jié)果 混合分布和未考慮其變異特性的整體時間序列的邊緣分布函數(shù)的擬合曲線如圖5所示。就年最大洪峰而言,混合分布擬合曲線的上部與單一擬合函數(shù)GEV和LLG存在較大差異,但混合分布擬合曲線上部更貼近洪水實測值能較好地描述洪水時間序列;年最大1 d洪量模擬中混合分布曲線的下部與單一擬合函數(shù)GP為一致,而其上部分布存在一定的差異。同時擬合曲線中部單一LLG分布擬合曲線有更大概率通過洪水實測值,但對于洪水極端事件,線性上尾分布是設(shè)計洪水?dāng)M合效果更佳的選擇。由于混合分布模型考慮了洪水序列的非一致性,采用兩條不同分布的子序列進(jìn)行擬合分布比傳統(tǒng)單一分布經(jīng)驗點據(jù)擬合效果更好,且更好地保證了洪水設(shè)計的安全需求。通過采用K-S擬合優(yōu)度檢驗,確定統(tǒng)計數(shù)據(jù)是否服從于5%顯著性水平的擬合分布,得出年最大洪峰與年最大1 d洪量混合分布對應(yīng)的D值分別為0.054和0.062,均小于臨界值D58,0.05=0.179,即混合分布函數(shù)均滿足假設(shè)檢驗,因此考慮變異情況下的混合分布擬合曲線是可行的。 圖5 邊緣分布概率擬合 考慮到變量間的相互依存關(guān)系,利用Pearson相關(guān)分析計算年最大洪峰和年最大1 d洪量的相關(guān)系數(shù)為0.846,由此可見,瑪納斯河流域肯斯瓦特水文站控制流域的年最大洪峰和年最大1 d洪量存在著較強的正相關(guān)性。利用貝葉斯框架中的馬爾可夫鏈蒙特卡羅(Markov chain Monte Carlo,MCMC)[32-33]模擬來估計其參數(shù)值。同時采用AIC、貝葉斯信息準(zhǔn)則(BIC)和Max-Likelihood(MAX-L)方法對聯(lián)合概率分布擬合優(yōu)度進(jìn)行檢驗,其結(jié)果見表3。 表3 Copula函數(shù)參數(shù)估計及擬合優(yōu)度 本文采用圖形分析法直觀地描述函數(shù)的擬合優(yōu)劣程度。將理論聯(lián)合概率值與經(jīng)驗聯(lián)合概率值點繪到同一張圖中,當(dāng)點集越靠近45°線,表明聯(lián)合分布模型擬合較好。其中兩變量經(jīng)驗聯(lián)合概率分布計算公式為 Femp(x,y)=P(X≤x,Y≤y)= (6) 式中:Femp為聯(lián)合經(jīng)驗概率;ngk為滿足X≤x、Y≤y的觀測值,其中g(shù)和k分別為兩實測數(shù)據(jù)從小到大排列后的序號;n為系列長度。其概率散點Q-Q圖見圖6。 圖6 經(jīng)驗聯(lián)合分布與理論聯(lián)合分布Q-Q圖 Gumbel Copula函數(shù)與兩參數(shù)函數(shù)BB1 Copula和BB5 Copula的理論與聯(lián)合概率點均落在45°對角線附近,起到了較為滿意的擬合效果;而Clayton Copula函數(shù)高頻率概率點偏差較大,擬合效果并不理想(圖6)。由表3可以得出:Gumbel Copula函數(shù)擬合年最大洪峰與年最大1 d洪量效果最好,其中AIC值為-433.963,BIC值為-431.902,均為各函數(shù)最低,這與圖形分析檢驗結(jié)果一致。因此,采用對變量分布上尾部變化較為敏感的Gumbel Copula函數(shù)進(jìn)行聯(lián)合是合理的。 分別取重現(xiàn)期10 a、20 a、50 a、100 a和500 a的年最大洪峰與年最大1 d洪量相互組合,并計算聯(lián)合分布概率,根據(jù)表1風(fēng)險概率模型計算其組合風(fēng)險概率,以此確定任一重現(xiàn)期標(biāo)準(zhǔn)的設(shè)計洪峰和設(shè)計最大1 d洪量組合的風(fēng)險情況。各量級洪峰和年最大1 d洪量組合的風(fēng)險概率計算結(jié)果見表4。 表4 各量級峰量組合風(fēng)險概率 表4中,當(dāng)洪水峰量組合為10年一遇時,即洪峰(565.882 m3/s)與年最大1 d洪量(0.369億m3)在相同低重現(xiàn)期的情況下聯(lián)合風(fēng)險(10.89%)與同現(xiàn)風(fēng)險(8.45%)最高,說明這種組合設(shè)計標(biāo)準(zhǔn)最為危險,同時也反映出該組合下防洪設(shè)計標(biāo)準(zhǔn)設(shè)置過低。在洪峰防洪設(shè)計標(biāo)準(zhǔn)一定的情況下,只要稍微提高洪量設(shè)計標(biāo)準(zhǔn),則3項風(fēng)險指標(biāo)均呈顯著下降趨勢。對于500年一遇峰量兩變量防洪設(shè)計標(biāo)準(zhǔn),聯(lián)合風(fēng)險與同現(xiàn)風(fēng)險均達(dá)到最小值,反映這種組合的設(shè)計標(biāo)準(zhǔn)相對最為安全,因此在高防洪設(shè)計標(biāo)準(zhǔn)下,洪水峰量共同影響下的洪水發(fā)生概率較低。 本文組合風(fēng)險概率是在“以洪峰為主”設(shè)計工況中洪峰變量Q沒有超過設(shè)計值q,而年最大1 d洪量變量W1超過設(shè)計值w1的概率。在500年一遇洪峰組合10年一遇洪量中,由于其年最大1 d洪量的設(shè)計標(biāo)準(zhǔn)偏低,故組合風(fēng)險增加,風(fēng)險概率達(dá)到最大值9.60%;若以10年一遇洪峰組合500年一遇洪量,500年一遇年最大1 d洪量遠(yuǎn)大于10年一遇洪峰設(shè)計標(biāo)準(zhǔn),故此組合風(fēng)險幾乎可以忽略不計,從而反映出該組合的設(shè)計標(biāo)準(zhǔn)相對安全,但這并不符合防洪設(shè)計需求。因此,選擇頻率較為接近的洪峰和洪量設(shè)計標(biāo)準(zhǔn)時,其風(fēng)險概率相對較小,且符合實際需求,如500年一遇的年最大洪峰和500年一遇的年最大1 d洪量的組合風(fēng)險概率僅為0.01%。 以流域500年一遇設(shè)計防洪標(biāo)準(zhǔn)為例,洪水峰量聯(lián)合重現(xiàn)期為322 a,聯(lián)合風(fēng)險概率為0.31%,即洪峰、洪量中至少有一個變量超過設(shè)定值時的概率為0.31%。其同現(xiàn)風(fēng)險概率為0.21%,即同時遭遇超過設(shè)計標(biāo)準(zhǔn)洪峰及洪量的重現(xiàn)期為476 a。組合風(fēng)險概率為0.01%,即洪峰量級未超過設(shè)計標(biāo)準(zhǔn),但年最大1 d洪量超過設(shè)計標(biāo)準(zhǔn)時的概率為0.01%。這表明在利用水庫對洪量進(jìn)行調(diào)節(jié)來分擔(dān)風(fēng)險效果的同時,也不能忽略洪峰對水工建筑工程的不利影響。根據(jù)肯斯瓦特水利樞紐工程實際防洪需求,對多個洪水變量間的相關(guān)作用進(jìn)行分析,能更準(zhǔn)確地掌握洪水防范效果,為瑪納斯河流域風(fēng)險評估提供參考。 a.瑪納斯河洪水峰量時間序列在1993年發(fā)生了顯著性跳躍變化;混合分布模型能有效地對非一致性洪水時間序列進(jìn)行模擬。 b.對于瑪納斯河流域,以高重現(xiàn)期參照下的峰量兩變量為防洪設(shè)計標(biāo)準(zhǔn),聯(lián)合風(fēng)險與同現(xiàn)風(fēng)險均能接近最小值,即在較高的防洪設(shè)計標(biāo)準(zhǔn)約束下,峰量共同影響的洪水發(fā)生概率較低。 c.根據(jù)實際工程需求,選擇頻率較為接近的洪水要素設(shè)計標(biāo)準(zhǔn),可降低其組合風(fēng)險概率,滿足低成本承受較大風(fēng)險的實際需求,考慮洪水多屬性的聯(lián)合特征可為防洪工程設(shè)計提供更為全面可靠的理論依據(jù)。3 結(jié)果與分析
3.1 洪水序列特征

3.2 混合分布擬合
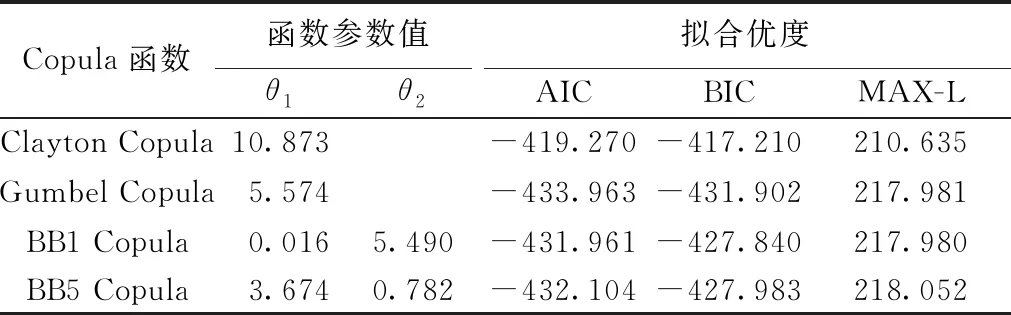
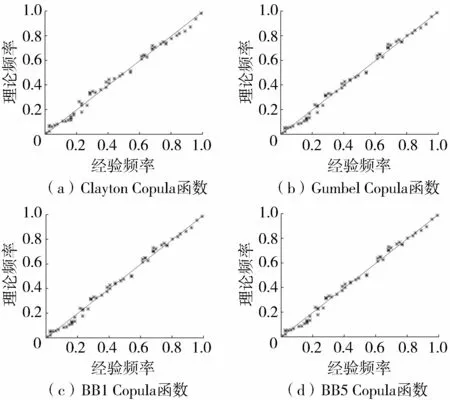
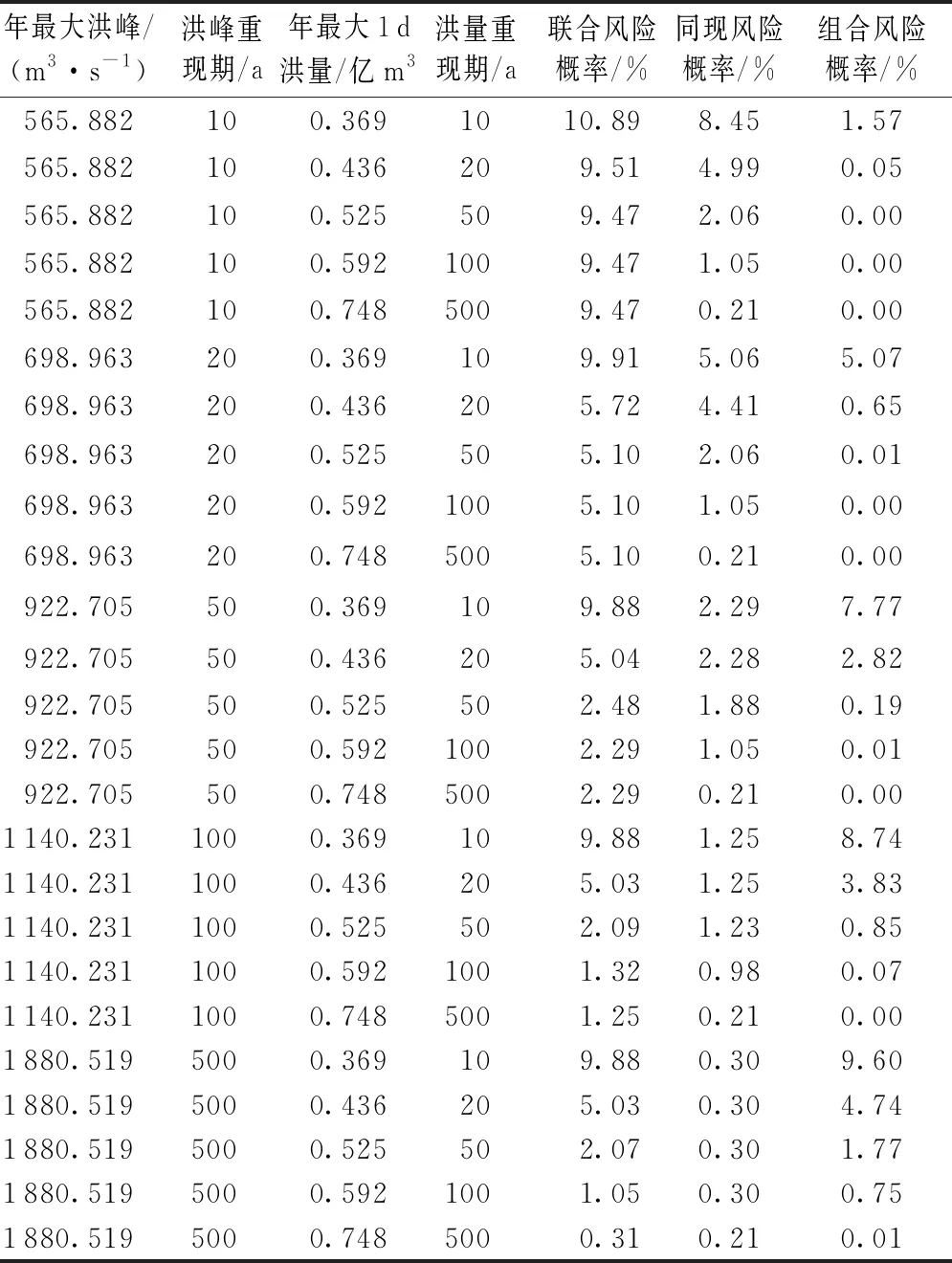
3.3 聯(lián)合分布及組合風(fēng)險
4 結(jié) 論

