水上滑坡沖擊涌浪的遠場傳播特征數值模擬分析

黃瑞啟，黃筱云,2，張少強，程永舟,2

(1.長沙理工大學水利與環境工程學院,湖南 長沙 410114; 2.水沙科學與水災害防治湖南省重點實驗室,湖南 長沙 410114)

庫岸邊坡失穩、崩落，滑坡體以一定速度沖擊水體，將產生巨大的涌浪。國內外滑坡浪事件屢見不鮮，如1963年意大利的瓦伊昂水庫滑坡[1]、2007年清江水布埡水庫大堰塘滑坡[2]、2008年長江巫峽龔家方滑坡[3]等。按照滑坡發生位置，可以將滑坡分為水上滑坡(subaerial)、水下滑坡(submarine)和濱水滑坡(partially submerged)3種類型[4]。與濱水滑坡、水下滑坡相比，水上滑坡會沖擊水面，涌浪的初始形態更加復雜，且與滑坡體運動與動力特征密切相關[5]。水上滑坡產生涌浪過程可分為以下4個階段[6]：①滑坡體開始移動、加速、沖擊水面；②滑坡體入水滑行產生涌浪；③涌浪向外傳播；④涌浪抵達岸線、爬高。按近場首波的非線性特征，滑坡涌浪大致可分為線性波、孤立波、橢圓余弦波和涌潮[7]，具體類型與滑坡體體積以及滑坡體與水之間的動量交換有關。

滑坡涌浪的特征研究主要采用理論分析[8-12]、物理模型試驗[13-19]和數值模擬[20-26]方法。現階段滑坡涌浪的數值模擬方法有基于N-S方程的數值模擬[27-28]、基于淺水方程的數值模擬[29-30]、基于Boussinesq波方程的數值模擬[31-32]和基于勢流方程的數值模擬[33-34]4類。若要完全模擬滑坡體沖擊水面造成水花飛濺和涌浪的傳播過程，基于N-S方程的數值模型是唯一選擇。基于N-S方程的數值模型又分為二維和三維兩類。在二維模型中，滑坡體寬度與水體寬度一致，涌浪只在一個方向上傳播；而三維模型可以呈現涌浪的不同徑向傳播。滑坡涌浪的三維數值模擬研究遠少于二維數值模擬研究，且滑坡涌浪傳播遠場特征的分析與討論較少見。

本文采用FLOW-3D軟件模擬水上滑坡產生涌浪的三維過程，分析不同徑向上周期與波高變化過程以及涌浪傳播近遠場的界限，并探討了遠場涌浪能量大小及其能量轉換率，以期為滑坡涌浪地質災害的預警提供參考。

1 數值模型及驗證

1.1 模型概況

三維滑坡涌浪模型(以下簡稱“本文模型”)采用FLOW-3D軟件建模，其中流體控制方程為不可壓縮流體運動的Navier-Stokes方程，采用標準RNGk-ε模型描述流體紊動特征，GMO模型控制滑坡體運動，TruVOF技術捕捉水面起伏和飛濺。通過調整GMO模型中的摩擦系數和碰撞系數可以改變滑坡體下滑、撞擊水面、觸底等狀態，以獲得準確的涌浪結果，碰撞系數取1表示碰撞物完全彈性，取0則是完全塑性。

1.2 模型驗證

通過與Liu等[35]的物理試驗結果對比來檢驗本文模型的有效性。該物理試驗在長104 m、寬3.7 m、高4.6 m的水槽中進行，槽內水深為3 m，滑坡坡度為27°，滑坡體長91 cm、寬65 cm、高46 cm，質量為475.52 kg，初始時刻滑坡體頂面距水面高度為0.46 m。本文模型采用漸變網格，最小網格尺寸是0.02 m，時間步長根據柯朗條件自動調整，摩擦系數和碰撞系數均取0.1。

圖1為6個測點(圖2)波面高度η實測結果與模擬結果的比較。總體上，本文模型模擬結果較Liu等[35]模擬結果更接近實測結果，說明本文模型各參數設置合理。

圖1 本文模型模擬結果與Liu等[35]模擬和試驗結果比較

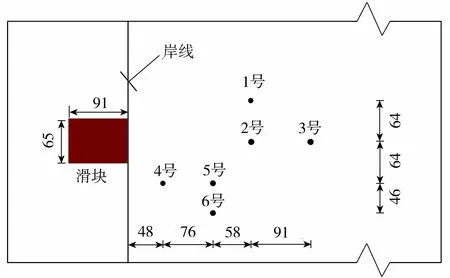
圖2 Liu等[35]物理試驗測點布置(單位：cm)

2 數值模擬試驗

2.1 試驗設置

整個試驗區域縱向長度設為200 m，水面橫向寬度為100 m，水深為10 m，滑坡坡度為45°。滑坡體為前緣角度為45°的四棱柱，長9 m、寬8 m、厚3 m，置于區域中線上，如圖3所示。為節省計算資源，將整個區域按中線分開，并將與中線重合的邊界設為對稱邊界，其余邊界設置為出流邊界，并布置多孔介質用于消波。

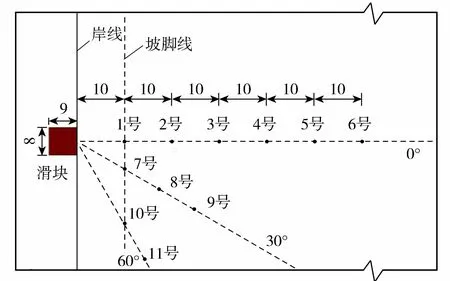
圖3 三維滑坡涌浪數值模擬試驗測點布置(單位：m)

2.2 數值模擬結果

滑坡涌浪的產生與傳播區域可以分為飛濺區、近場和遠場。一般而言，入水點至滑坡體停止點的水域屬于飛濺區；從停止點開始，波浪出現色散的區域稱為近場；呈現振蕩波特點的區域則為遠場[5]。就本文數值模擬試驗而言，坡腳線可以看作飛濺區與近場的界限。為獲取滑坡涌浪近遠場涌浪三維特征，在0°徑向上等間距布置6個測點，30°徑向上布置3個測點，60°徑向上布置2個測點，如圖3所示，其中，2、8號測點和10號測點徑距一致，3、9號測點和11號測點徑距相等。表1為滑坡體以4 m/s初始速度下滑時各測點的首、次波波峰高度ηc與周期T模擬結果。

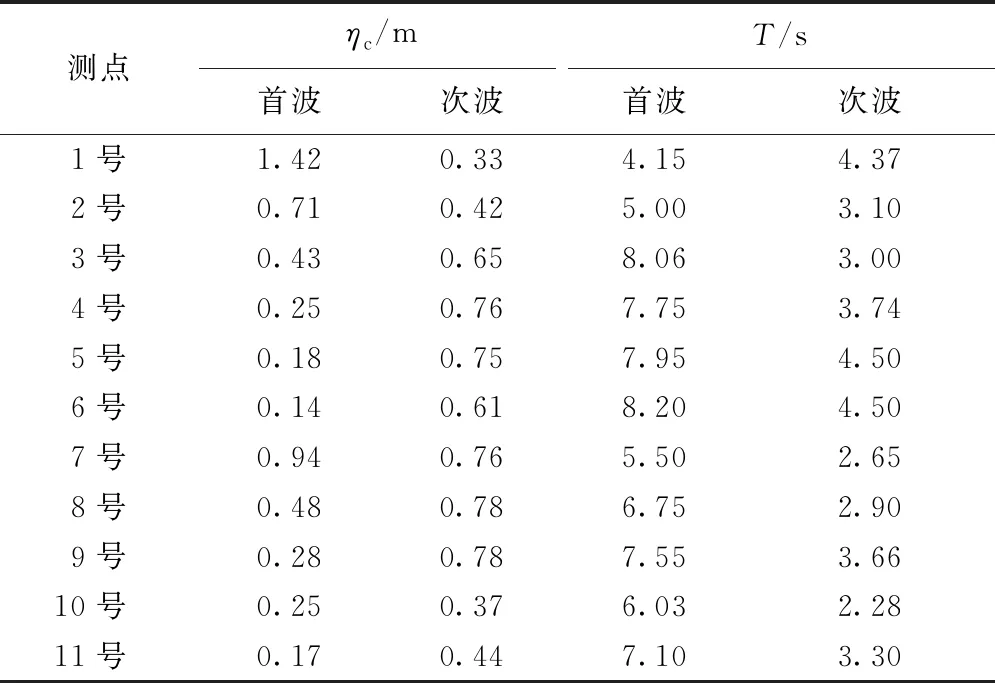
表1 各測點首、次波波峰高度與周期

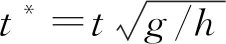
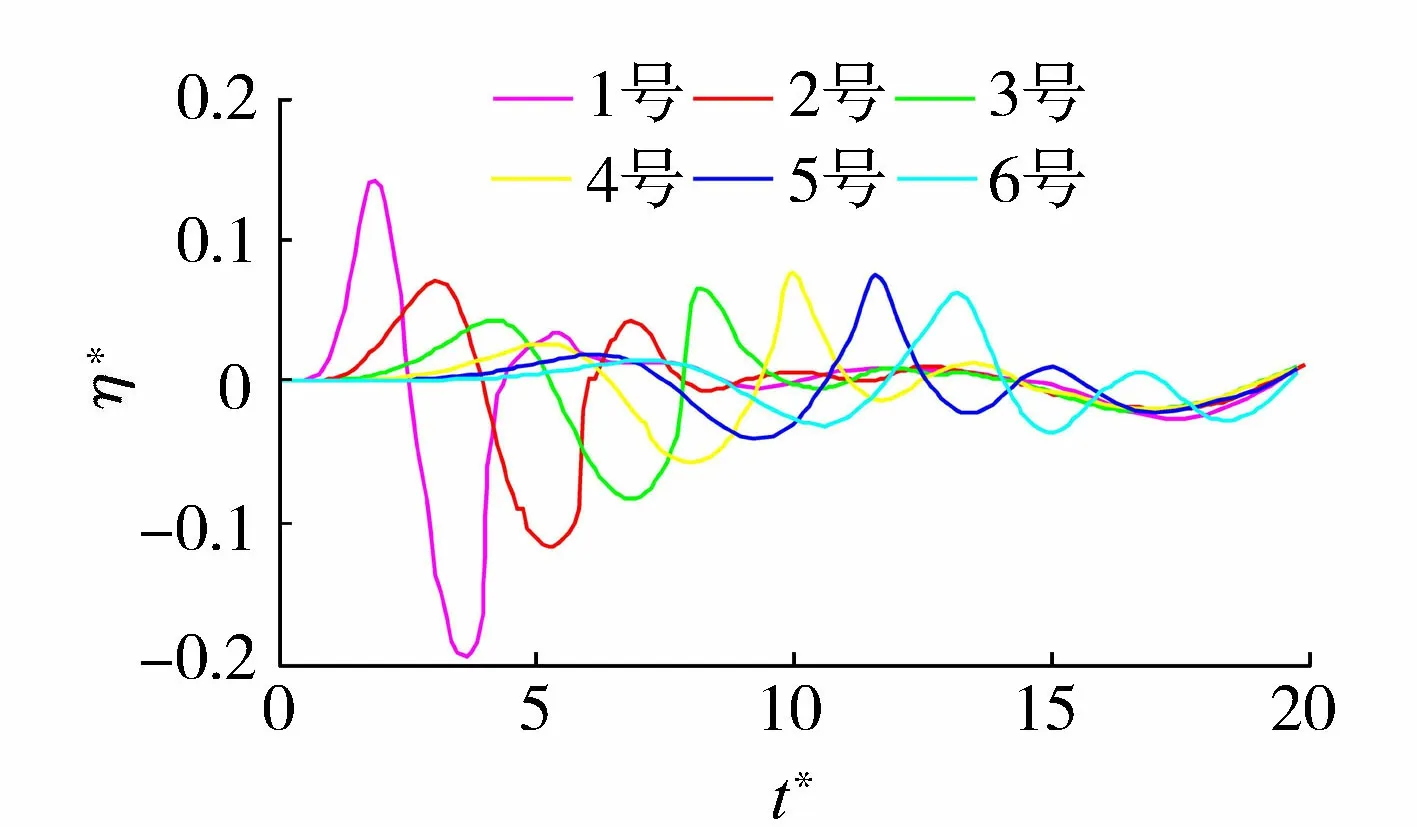
圖4 0°徑向各測點波面時程變化

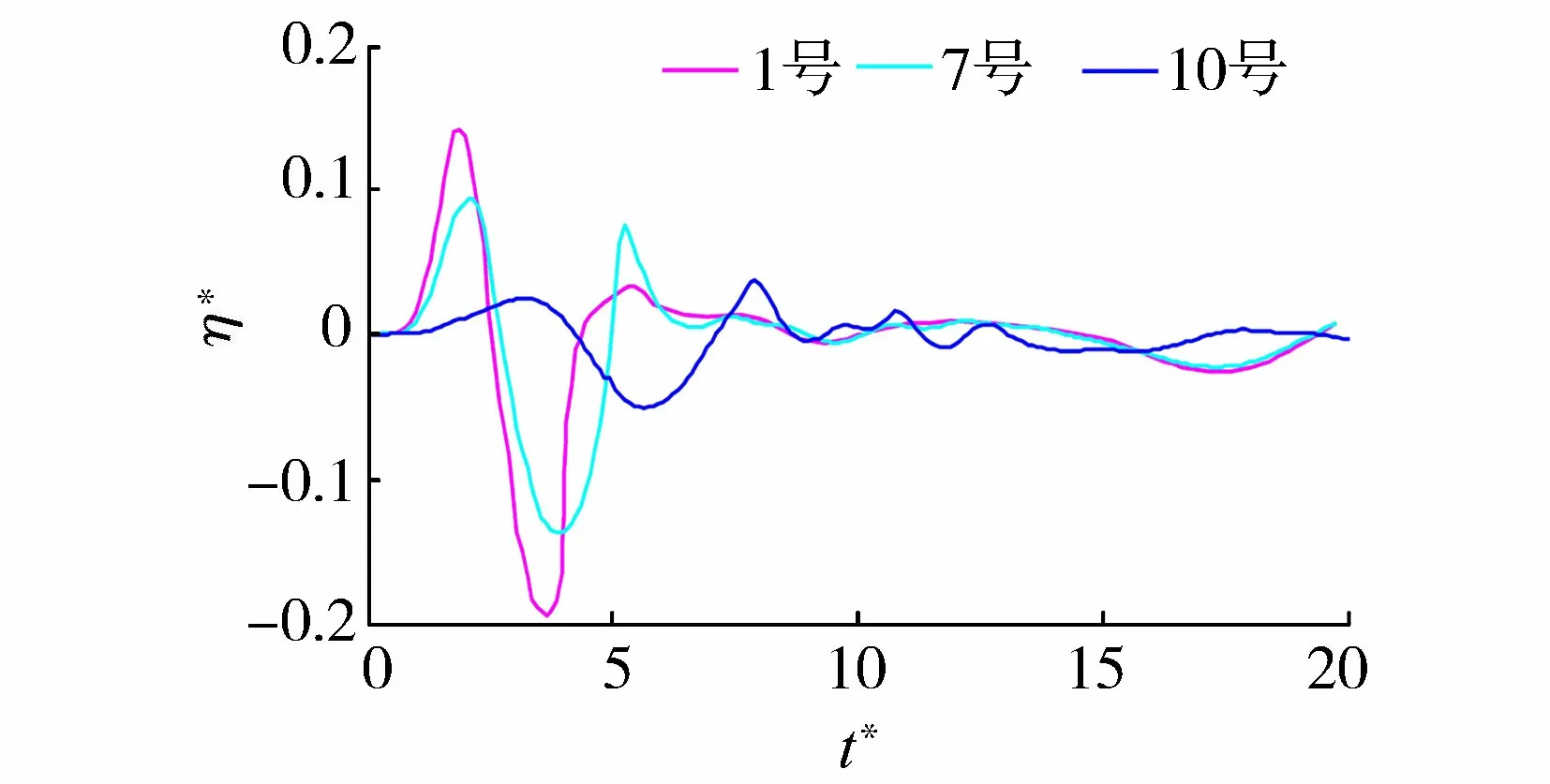
圖5 坡腳各測點波面時程變化

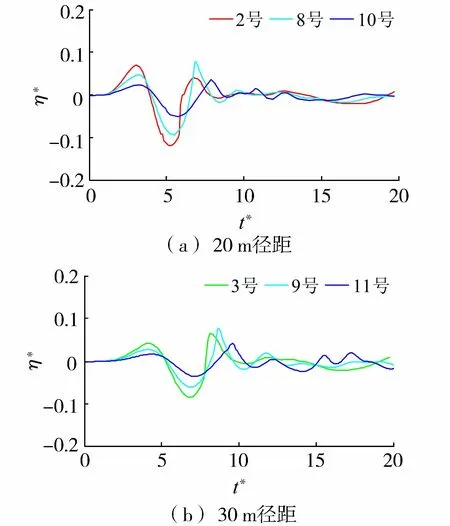
圖6 不同徑向等徑距測點波面時程變化

3 滑坡涌浪特征分析

為分析滑坡涌浪特征，本文通過改變滑坡體厚度s、寬度b與入水速度v以獲得不同的涌浪形態，數值模擬試驗具體工況見表2。

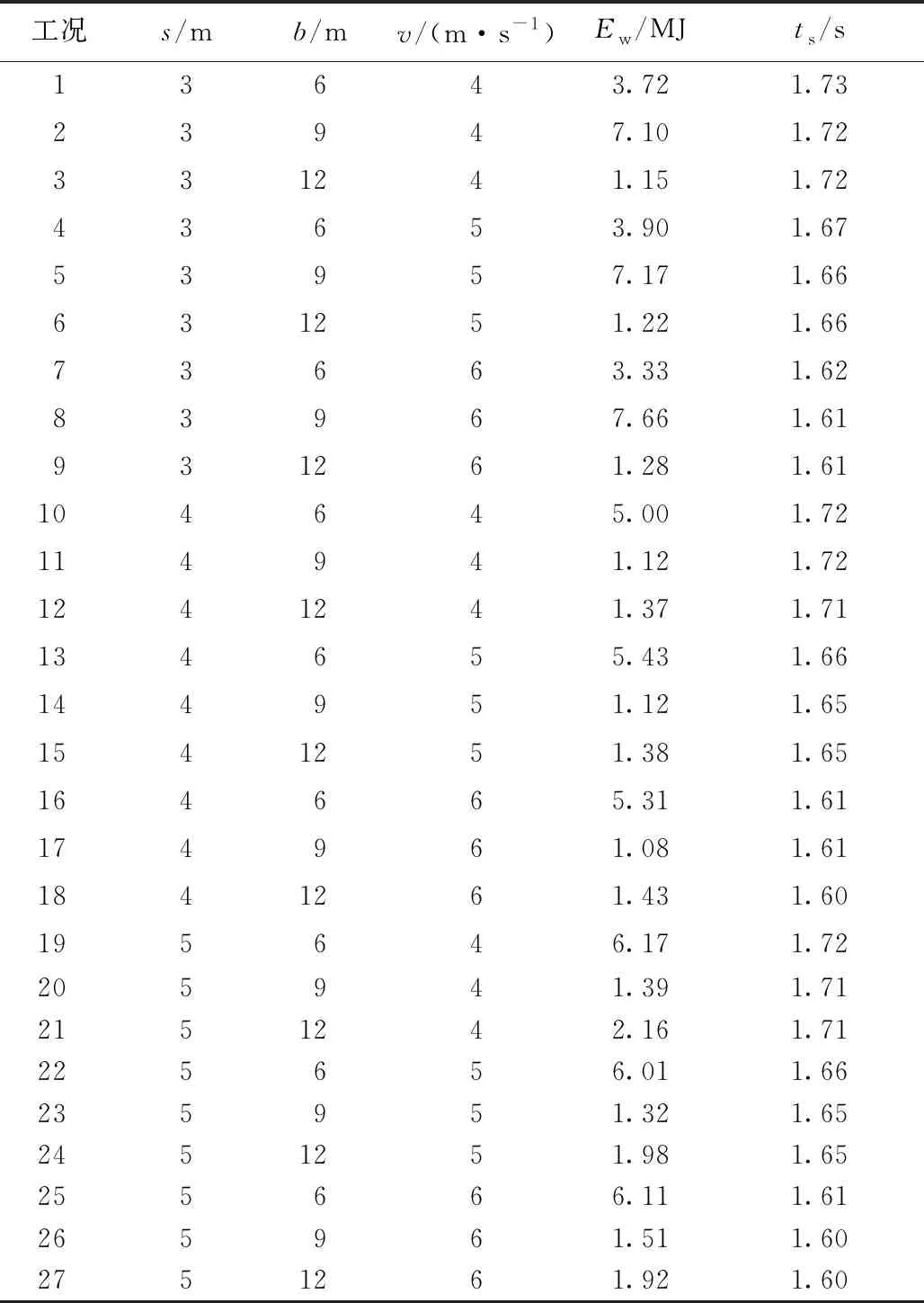
表2 數值模擬試驗工況與結果

3.1 滑坡體運動

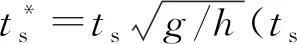
(1)

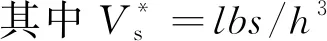
式中l為滑坡體長度。由于滑坡體下滑主要受到水體的正面阻力，若不考慮側向阻力，有

(2)

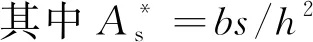
根據27組工況的滑坡體滑坡特征時間數值模擬結果(表2)，相對滑坡特征時間的擬合公式為

(3)

式(3)的擬合度為0.991，均方誤差為3.47×10-4。

3.2 近遠場

Walder等[5]將近場定義為從飛濺區邊界至涌浪動能與勢能趨近于某一漸近值的位置，Watts[13]則采用如下能量積分表示通過位置x斷面的涌浪總勢能：

(4)

當上述積分沿程趨近一定值時，便可確定近場的外邊界。圖7～9為不同徑向上沿程各測點的涌浪總勢能(圖中s*=s/h為滑坡體相對厚度，b*=b/h為滑坡體相對寬度)，橫坐標x*=x/h。可以看出，總勢能沿程減小，其中，弗勞德數對近場總勢能的沿程變化影響較小，而相對厚度與相對寬度的影響明顯。在1～3倍水深之間，總勢能的下降幅度較大，而后下降幅度開始減少，當涌浪達到6～7倍水深區間時，各徑向涌浪總勢能變化較小，且在7倍水深位置不同徑向的涌浪總勢能幾乎相等。因此，7倍水深距離可看作三維滑坡涌浪近場的外邊界。

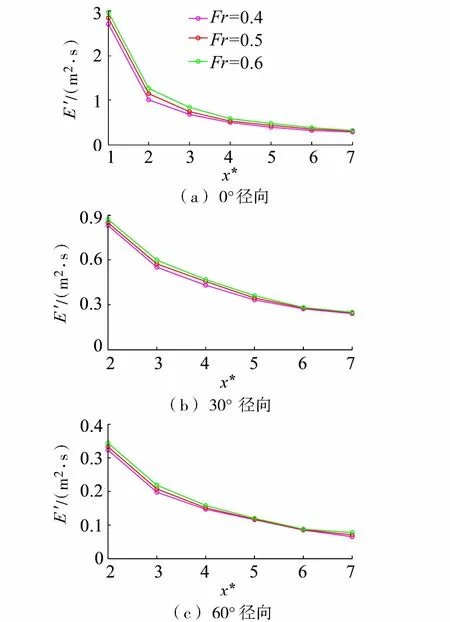
圖7 不同滑坡體弗勞德數下各徑向涌浪能量積分沿程變化

圖8 不同滑坡體相對厚度下各徑向涌浪能量積分沿程變化

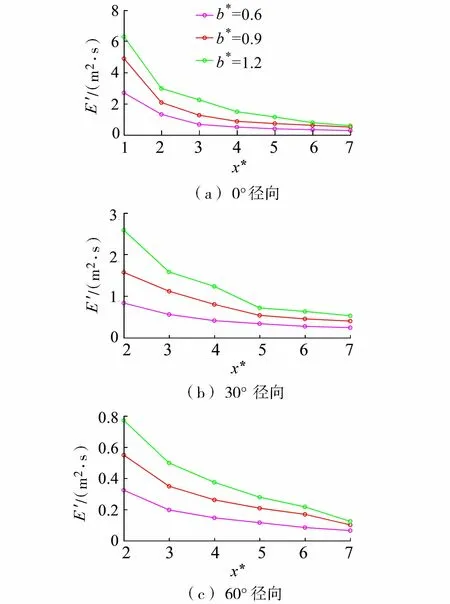
圖9 不同滑坡體相對寬度下各徑向涌浪能量積分沿程變化

3.3 波峰高度

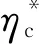
(5)

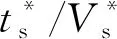
(6)

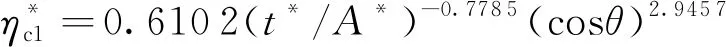
(7)

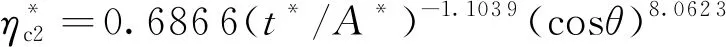
(8)

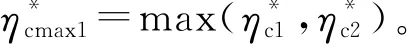
在遠場，涌浪幾乎以固定頻率傳播，遠場涌浪最大波幅將出現在近遠場交界處。取徑距為7倍水深位置作為遠場起始位置，最大相對波峰高度出現在次波，其試驗值與預測值關系如圖10所示，其擬合公式為

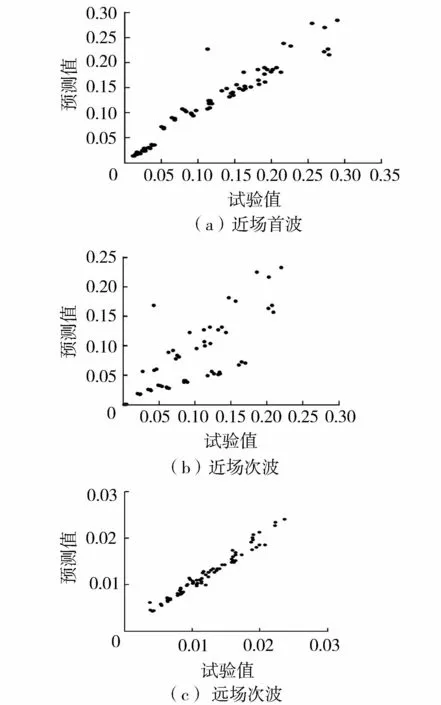
圖10 近遠場相對波峰高度試驗值與預測值關系

(9)

式(9)的擬合度為0.984 5，均方誤差為7×10-7。

3.4 周期

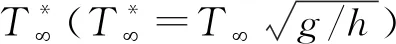
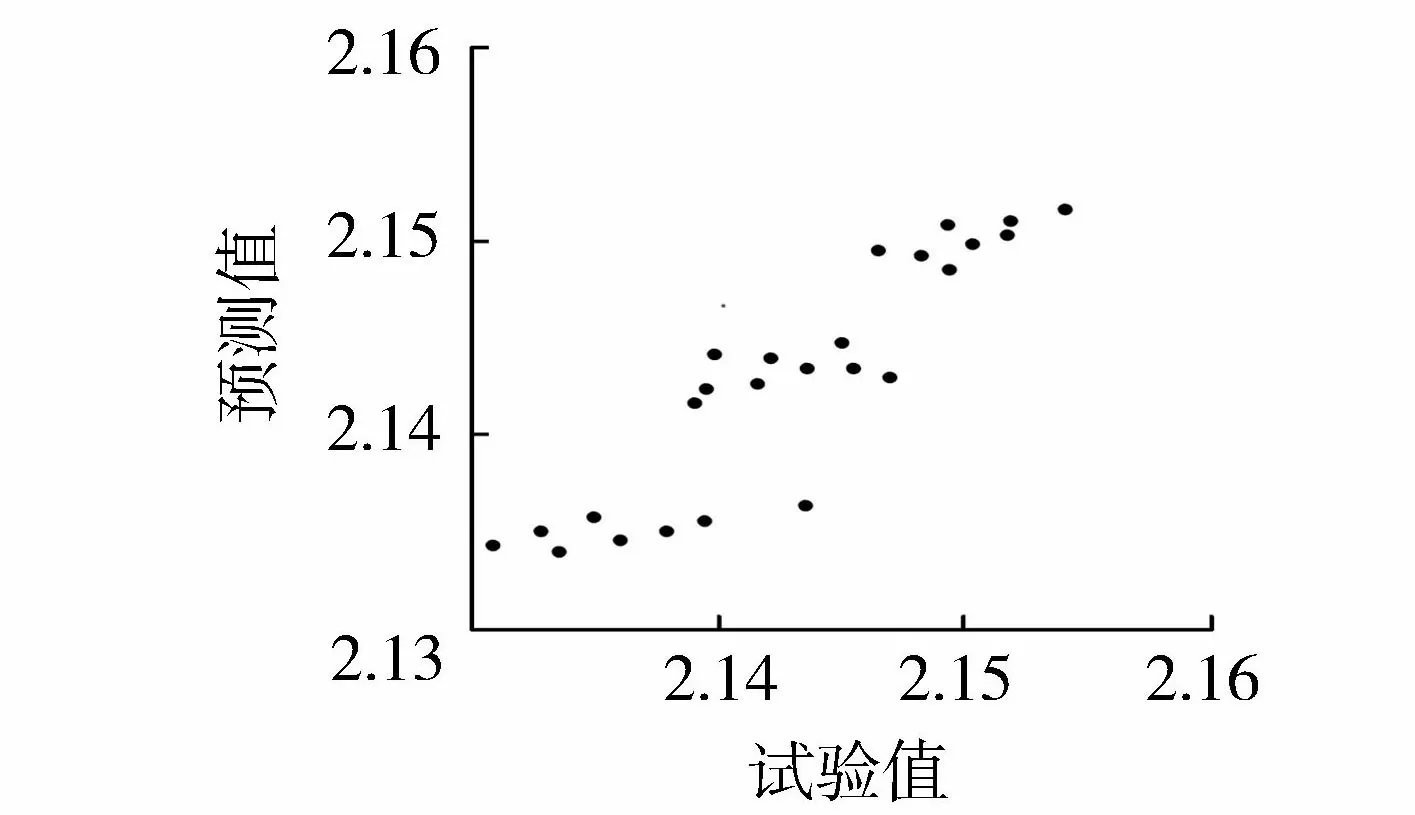
圖11 遠場次波相對周期試驗值與預測值的關系

(10)

式(10)擬合度為0.85，均方誤差為7×10-6。

3.5 波形

遠場涌浪的相對波長為

(11)

根據式(9)(10)(11)，推導出遠場涌浪非線性Ursell數公式為

(12)

式中波高H近似為波幅的2倍。27組工況數值模擬試驗得到的Ursell數如圖12所示,不難發現，遠場涌浪均屬于線性波。

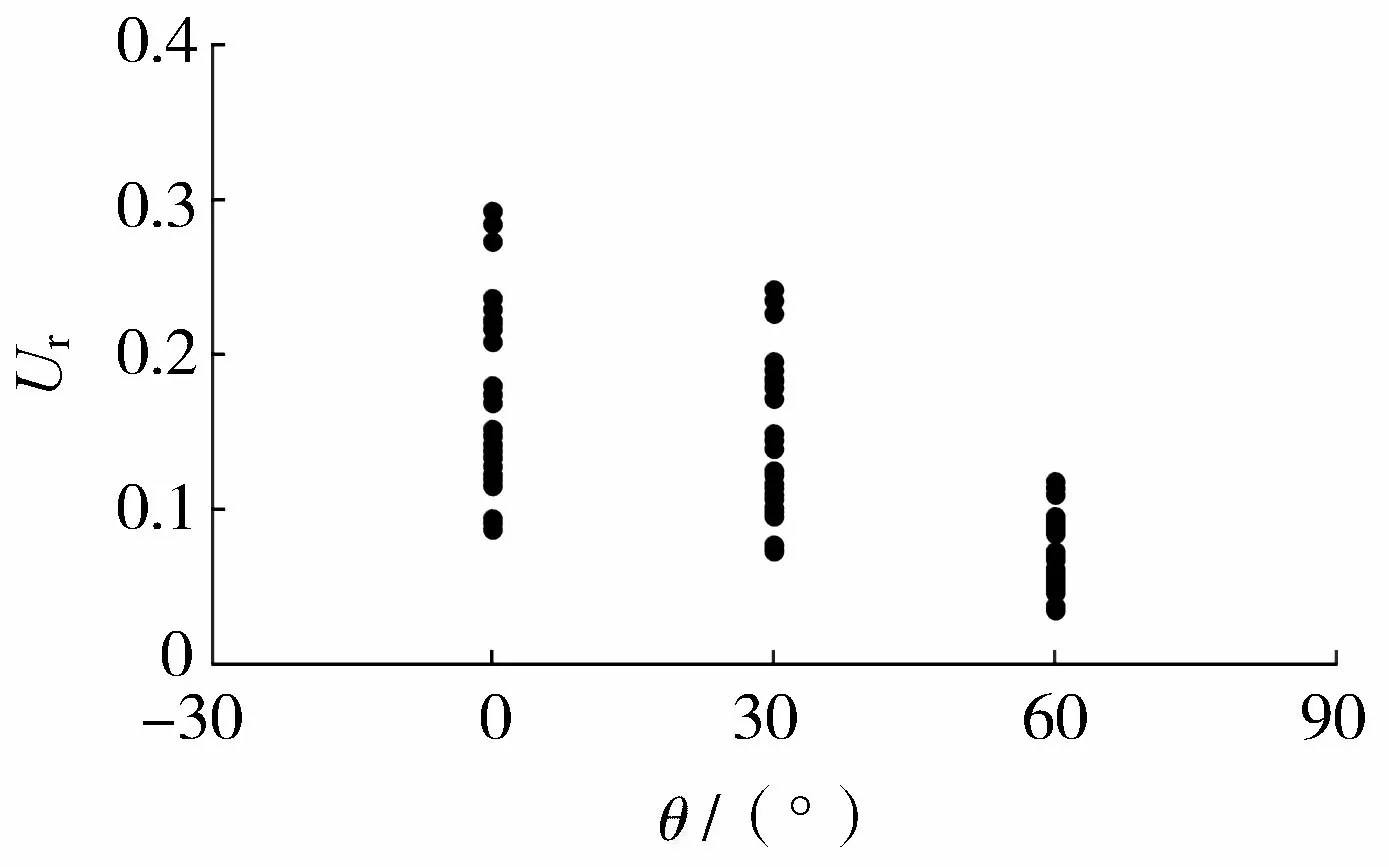
圖12 各徑向遠場涌浪的Ursell數

3.6 遠場涌浪能量

計算遠場涌浪能量對滑坡涌浪災害的預測評估具有重要的影響。通過徑距為R處的半圓斷面的涌浪總勢能Ep(R)為

(13)

根據線性波理論，遠場涌浪的勢能與動能相同，故通過遠場斷面(R=7h)的涌浪總能量Ew=2Ep，27組工況的近遠場分界斷面涌浪總能量見表2。涌浪的總能量來自于滑塊的能量，包括動能和勢能，故定義能量傳遞率ε為遠場涌浪能量與滑坡體能量的比值(ε=Ew/Es，其中Es為滑坡體的能量)。計算結果表明，27組工況的能量傳遞率在8.0%～19.7%之間。能量傳遞率主要與波峰高度時程變化有關，根據數值模擬結果，擬合的能量傳遞率公式為

ε=0.295 1(t*/A*)-0.503 4

(14)

式(14)的擬合度為0.860 1，均方誤差為2.08×10-4。能量傳遞率的試驗值與預測值關系見圖13。

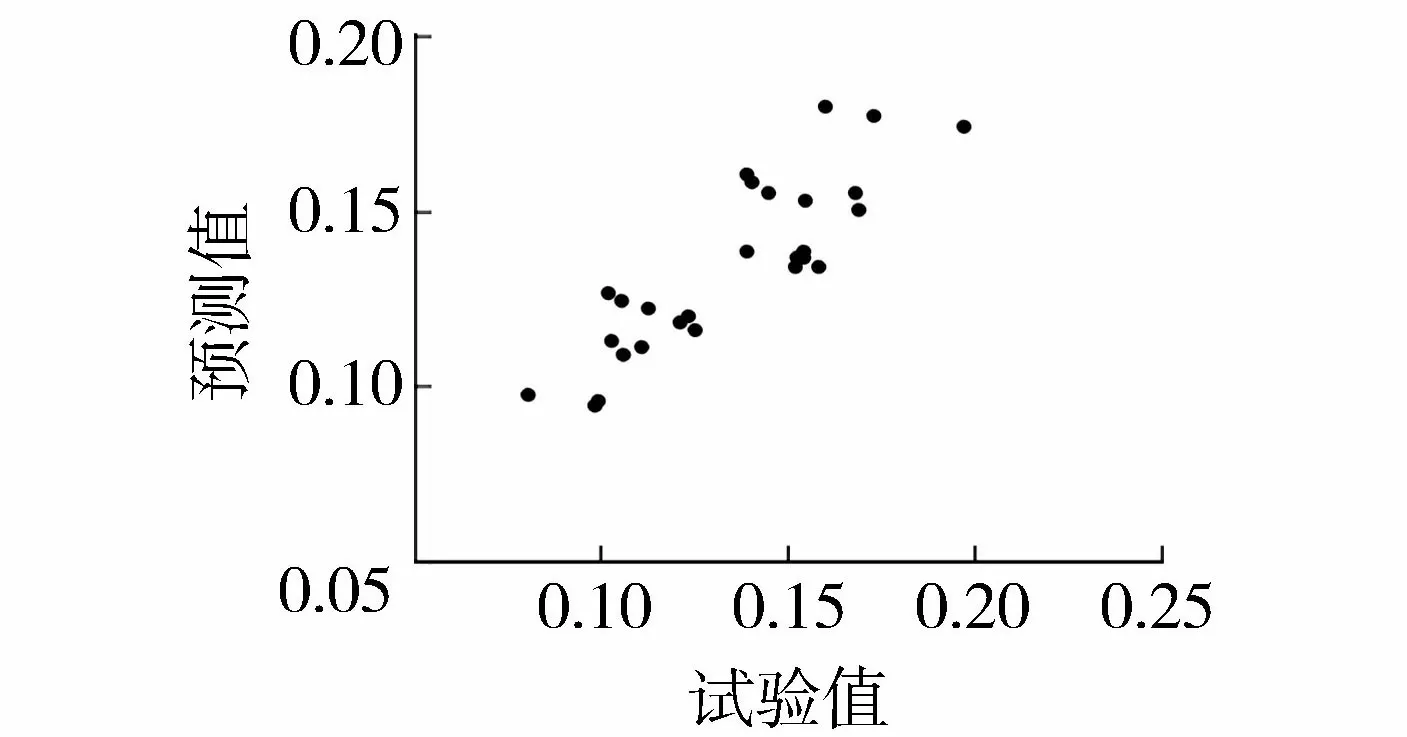
圖13 能量傳遞率的預測值與試驗值的關系

4 結 論

a.三維滑坡涌浪在不同徑向上均出現衰減，但在7倍水深距離后保持穩定，該距離外的波峰高度基本與滑坡體弗勞德數、厚度以及寬度無關，故可認為沖擊滑坡涌浪的近遠場界線位于7倍水深處。

b.相對滑坡特征時間是滑坡體弗勞德數、斜坡角度以及相對滑坡體尺寸的函數，決定了近遠場最大波峰高度和遠場次波周期的大小，也對遠場次波的非線性特征有一定影響。

c.定義了滑坡體的能量傳遞率，本文工況中能量傳遞率在8.0%～19.7%之間。