面向管材存儲的自動化立體倉庫貨位優化

屈新懷,紀 飛,丁必榮,孟冠軍

(合肥工業大學 機械工程學院,安徽 合肥 230009)

0 引 言

自動化立體倉庫(automated storage and retrieval system,AS/RS)是現代倉儲技術、計算機技術和自動化技術高度集成的產物。它能夠加快貨物流轉,縮短生產周期,進而降低企業制造成本,是各類制造企業向著智能化轉型不可或缺的倉儲形式[1]。同時,汽車制管廠作為車企的一個重要組成部分,其主要職能是為各類汽車提供各類管材,如制動管路、動力轉向管路、燃油管路、空調管路等。由于管材的種類多、尺寸長、致使存儲困難,因此將汽車制管廠倉庫改造為AS/RS是車企向智能化轉型的一個重要步驟。

在AS/RS的研究中,貨位優化是影響其性能的一個關鍵因素[2]。文獻[3]面向船舶行業,提出了一種以出庫效率、貨架穩定性、巷道負載均衡為目標的貨位優化模型;文獻[4]對于電子產品的存儲,建立了一種以提高堆垛機存取效率和貨架穩定性為目標的貨位優化模型;文獻[5]基于液壓元器件的存儲,考慮了貨架穩定性、平衡性和出庫效率,建立了貨位優化模型;文獻[6]基于防洪物資及其存儲特點,建立了反映檢索效率和貨架穩定性為目標的貨位優化模型。

結合上述文獻可以看出,目前國內外對貨位優化方面的研究主要集中在尺寸較短同時包裝成塊狀的材料,并且貨架主要是單元格式貨架。對尺寸較長的管材和適合存放管材的懸臂式貨架[7]的研究很少。因此,本文基于懸臂式貨架進行管材的貨位優化,從存取效率、貨架穩定性和貨架平衡性出發建立貨位優化問題的數學模型,進一步設計求解該模型的啟發式算法,并采用某汽車制管廠的數據進行實例仿真。

1 問題描述

根據管材尺寸較長、種類較多、質量不一的特點,采用懸臂式貨架進行存放,構建出AS/RS立面示意圖,如圖1所示。堆垛機從出入口(I/O)出發,可沿X、Y、Z方向進行作業并沿原路徑返回,其中X、Y、Z分別代表貨架的排方向、列方向、層方向。

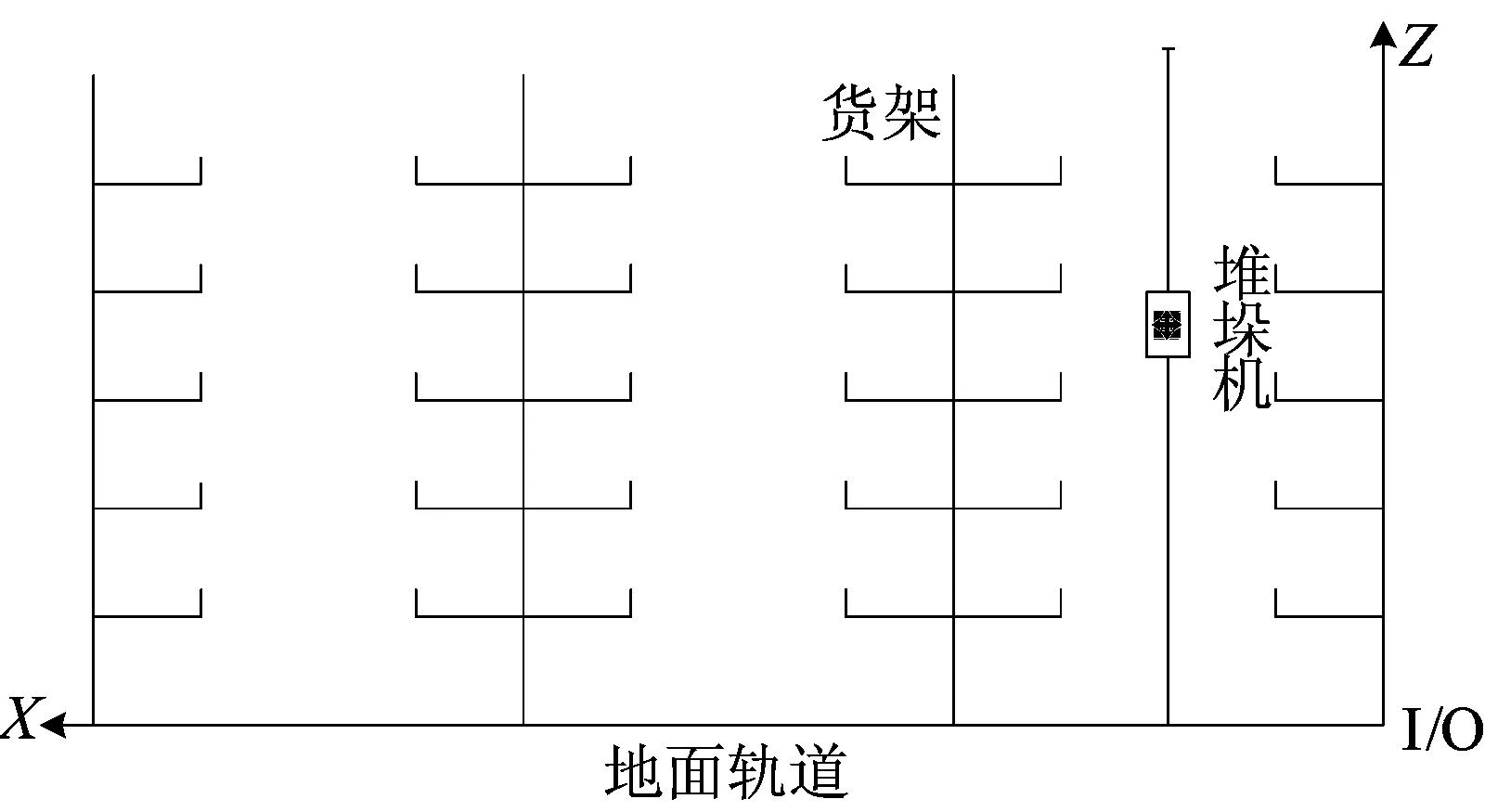
圖1 AS/RS立面示意圖

為了提高AS/RS的存儲效率,保證其貨位分配的合理性和安全性,需要使用恰當的貨位分配原則,因此提出了以下貨位分配的優化原則:

(1) 存取效率原則。將周轉率較高的管材放置在離出入口較近的位置,以減少堆垛機行程,從而提高AS/RS的存取效率。

(2) 穩定性原則。將質量較大的管材放置在貨架的低層,將質量較小的管材放置在貨架的高層,從而降低貨架的整體重心。

(3) 平衡性原則。考慮管材的質量和懸梁臂貨架的結構特點,需要考慮貨架的平衡性,以保證AS/RS具有足夠的安全系數[8]。

為了方便AS/RS模型構建和問題研究,基本假設如下:

(1) 倉庫只有1個出入庫端口,堆垛機只進行單一作業。

(2) 堆垛機勻速運行,不考慮加減速,不考慮堆垛機存取貨物的時間,不考慮堆垛機與運輸設備的交接時間。

(3) 每個貨位只存放1種管材,且貨位與管材尺寸相匹配。

2 AS/RS貨位優化模型建立

2.1 模型參數

貨物位置采用三維坐標(x,y,z)表示,即貨物在倉庫的第x排y列z層。倉庫沿X方向共有a排,沿Y方向共有b列,沿Z方向共有c層。設定堆垛機沿X方向的速度為vx,沿Y方向的速度為vy,沿Z方向的速度為vz;單位貨格沿X方向的長度為l,沿Y方向的寬度為w,沿Z方向的高度為h;貨架之間巷道的寬度為L;貨位(x,y,z)上貨物的質量為mxyz,周轉率為pxyz,決策變量為dxyz,即當貨位(x,y,z)上有貨物時dxyz為1,否則為0。

2.2 多目標貨位優化模型建立

根據管材和懸臂式貨架的結構特點,同時結合上文提出的貨物的存取效率、貨架的穩定性和平衡性3個貨位分配原則,建立多目標貨位優化模型。

2.2.1 提高存取效率

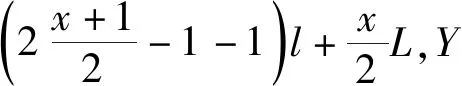
(1)

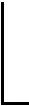
2.2.2 提高貨架穩定性

采用上輕下重的原則存放貨物以降低貨架的整體重心,從而提高貨架的穩定性,其數學模型可描述為:

(2)

2.2.3 提高貨架平衡性

基于貨物載荷和懸梁臂式貨架的結構特點,應該盡量使貨架兩側載荷均衡,以提高貨架的平衡性,其數學模型可描述為:

minf3=

(3)

2.3 權重系數分配

通過賦予權重系數,可以將復雜的多目標函數優化問題轉化為單目標函數優化問題，以便于求解。由于3個目標函數的量綱不一致,在分配權重系數前先采用反正切函數轉換法對3個目標函數做歸一化處理,得到minf1′、minf2′、minf3′,則單目標數學模型可描述為:

minf=w1minf1′+w2minf2′+w3minf3′;

s.t.w1+w2+w3=1,

0≤w1≤1,

0≤w2≤1,

0≤w3≤1

(4)

權重系數w1、w2、w3的取值采用層次分析法[9]確定,經過分析設定判斷矩陣為:

求解得到3個目標函數的權重系數分別為0.17、0.63、0.20,最終獲得的單目標數學模型可描述為:

minf=

0.17minf1′+0.63minf2′+0.20minf3′

(5)

3 貨位優化算法設計

傳統粒子群算法(particle swarm optimization,PSO)僅需速度和位置的迭代進化就可以逼近全局最優解,其原理簡單且運行高效,比較適合求解本文的貨位優化問題,文獻[10-11]均采用了PSO進行貨位優化方面的研究,并且通過實驗取得了良好的優化結果。傳統PSO中粒子i的迭代過程可描述為:

(6)

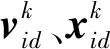
同樣廣泛應用于自動化立體倉庫貨位優化問題的還有全局尋優能力強、魯棒性高的遺傳算法(genetic algorithm,GA)。

但是考慮到PSO搜索精度不高、局部搜索能力差且易陷入局部最優的缺陷[12]以及GA收斂速度慢、控制變量多、易早熟的問題，本文構建了PSO與GA的混合算法,即粒子群遺傳算法(PSOGA),進行貨位優化分析。

PSOGA通過將GA算法中合適的變異算子、交叉算子與PSO算法相結合[13],可以保證種群中個體的多樣性,擴展算法的搜索范圍,從而增強PSOGA的局部搜索能力,并在一定程度上提高解的質量。PSOGA的具體實現流程如圖2所示。

圖2 PSOGA流程

PSOGA的具體實現步驟如下:

(1) 將需要入庫的貨物看作一個個粒子,對其隨機分配初始貨位并給予初始速度,形成初始種群,每個帶有位置和速度信息的粒子作為種群的個體。

(2) 以(5)式作為適應度評價函數,計算種群中各個體的適應度值,選出個體最優和全局最優。

(3) 以(6)式作為迭代公式,更新種群中個體的位置和速度,選出新的個體最優和全局最優。

(4) 對迭代更新后的種群執行GA中的選擇、交叉、變異操作。其中選擇操作采用錦標賽選擇法,交叉操作采用兩點交叉,變異操作選取逆轉變異算子。

(5) 重新根據(5)式計算適應度值,并判斷是否滿足終止條件;滿足則接受當前解,并獲取貨位優化后倉庫的信息,不滿足則循環以上操作。

4 實例計算與仿真分析

以某汽車品牌制管廠倉庫的實例數據進行仿真分析,倉庫的基本參數信息見表1所列。

表1 倉庫基本參數

選取16種不同的管材進行貨位優化分析,管材基本信息見表2所列。

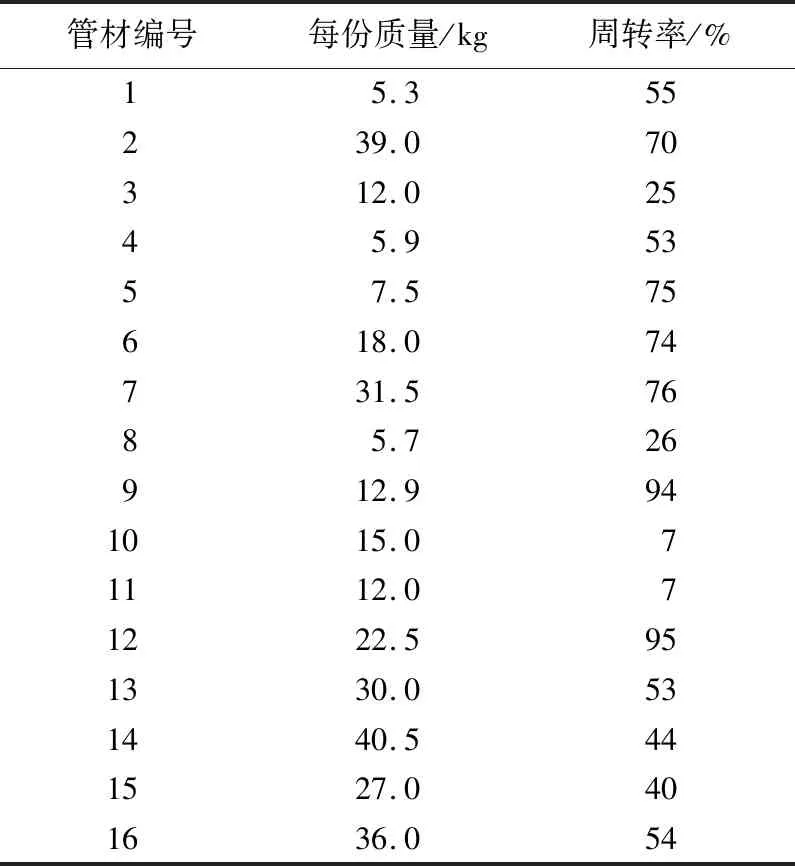
表2 管材數據信息

經過分析比較設定PSOGA中的參數為:加速度常數c1=c2=1;r1、r2選取0～1之間的隨機數;慣性權重α采用線性遞減權值法確定,最大值和最小值分別設定為1.0和0.8;種群數量為50;迭代次數N為200;選擇概率為0.8;變異概率為0.1。

第i次迭代的慣性權重α可描述為:

(7)

使用MATLAB分別運行GA、PSO、PSOGA算法,求解得到的具體目標函數值見表3所列,同時得到3種算法迭代收斂的對比結果,如圖3所示。

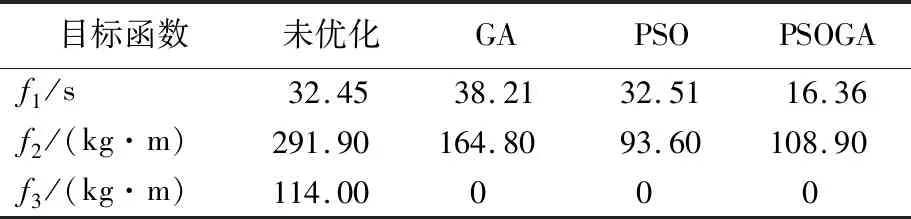
表3 目標函數值優化結果對比

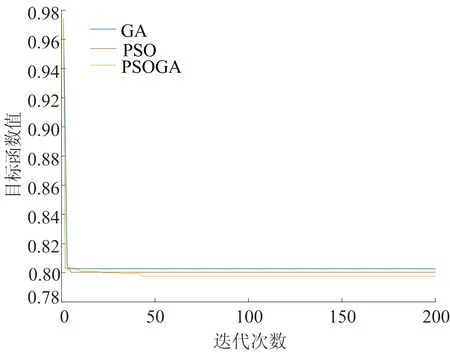
圖3 3種算法迭代收斂對比結果

觀察表3數據可以看出,相較于未優化前，經過3種算法優化后的目標函數值在貨架的平衡性和穩定性上均有大幅度提升,但在存取效率方面,GA和PSO的優化并不理想,只有PSOGA具有較好的優化結果;同時結合圖3的迭代收斂對比結果可以發現,PSOGA雖然收斂稍慢,但其歸一化后的總目標函數值小于其余2種算法,即解的綜合質量高于GA和PSO算法,且不易陷入局部最優。因此選用PSOGA進行貨位優化具有一定的優越性。

PSOGA算法優化前、后倉庫的貨位分配示意圖如圖4所示。

分析計算表3數據可得,相較于未優化前,經PSOGA優化后存取效率提高49.58%,貨架穩定性提高62.69%,貨架平衡性提高100%。從圖4可以看出,經PSOGA優化后的貨位分配明顯更加合理。

圖4 PSOGA優化前、后貨位分配圖

5 結 論

本文面向管材存儲構建了AS/RS模型研究貨位優化問題。根據管材特點采用懸臂式貨架進行存儲并選取了合適的貨位分配策略和原則,建立了貨位優化的多目標數學模型;通過MATLAB編程并采用PSOGA求解,獲得了全局最優解。結果表明,本文方法有效且切實可行,能夠較全面地提高倉庫的存取效率、貨架穩定性和平衡性。本文對面向管材存儲的AS/RS研究具有一定的理論和實踐意義。