水平管流中水合物顆粒運移和沉積數值模擬

馮明 FENG Ming

（中海石油（中國）有限公司海南分公司，海口 570100）

0 引言

水合物流動保障問題已成為制約深水油氣開發的關鍵問題之一[1]。深海淺部地層具有低溫高壓環境，容易在生產管柱中生成水合物，沉積并附著在管壁上，導致井筒出現水合物堵塞風險。研究水合物顆粒的運移和沉積規律對探究水合物堵塞的機理具有重要意義。

Lingelem等人（1994）提出了天然氣主導體系中水合物生成沉積的概念機理，在初始結晶階段，水分子和氣體分子分散在冷管管壁，形成亞臨界核，進而生長為晶體；隨著水分子與氣體分子不斷擴散，晶體持續生長，最終形成水合物堵塞[2]。Turner等人（2005）針對氣液共存系統建立了水合物動力學模型：CSMHyK模型，將過冷度和氣液接觸面積考慮在內[3]。Jassim等人（2010）使用CFD技術模擬了單水合物顆粒沉積的實驗，并提出了一種計算氣主導系統中單水合物顆粒沉降的理論模型[4]。Di Lorenzo等人首次對管道內環形霧流中的水合物形成和輸送進行了室內實驗研究，并獲得了大量實驗數據，如水合物形成速率、管壁上的水合物層生長速率等[5]。Wang等人討論了環霧流中的水合物沉積特征，并初步發現，氣芯中液滴產生的水合物顆粒和管壁液膜處產生的水合物顆粒均會沉積并粘附在管壁上[6]。

目前少有研究關注水合物顆粒在氣相中在管壁附近的運動狀態。本文利用優化的DPM模型模擬了水合物顆粒在氣芯中的運移和沉積特征，得到了水合物顆粒的運移和沉降特征，為準確預測水合物沉積堵塞提供了理論依據。

1 求解模型

氣井井筒以環霧流為主，氣相連續分布，液相以管壁液膜與氣核液滴形式存在，兩種形式均為水合物生成創造了條件，如圖1所示。研究該體系水合物沉積機理，必須綜合考慮液膜與氣核液滴中顆粒群的沉積。液膜中由于自由水存在，顆粒與壁面間的粘附力很大，水合物將直接沉積于壁面，前人對此研究做的工作較充分，本文主要針對氣核液滴中的水合物顆粒沉積機理展開研究。

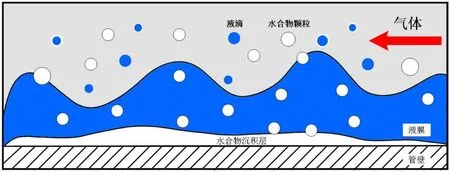
圖1 環霧流體系水合物顆粒沉積示意圖

本文采用的數值模型主要是離散相模型（DPM），顆粒力平衡方程的形式由公式（1）表示，該式右邊第一項為顆粒單位質量力，第二項是重力項，第三項是粒子其他力[7]，水合物顆粒受力示意圖見圖2。

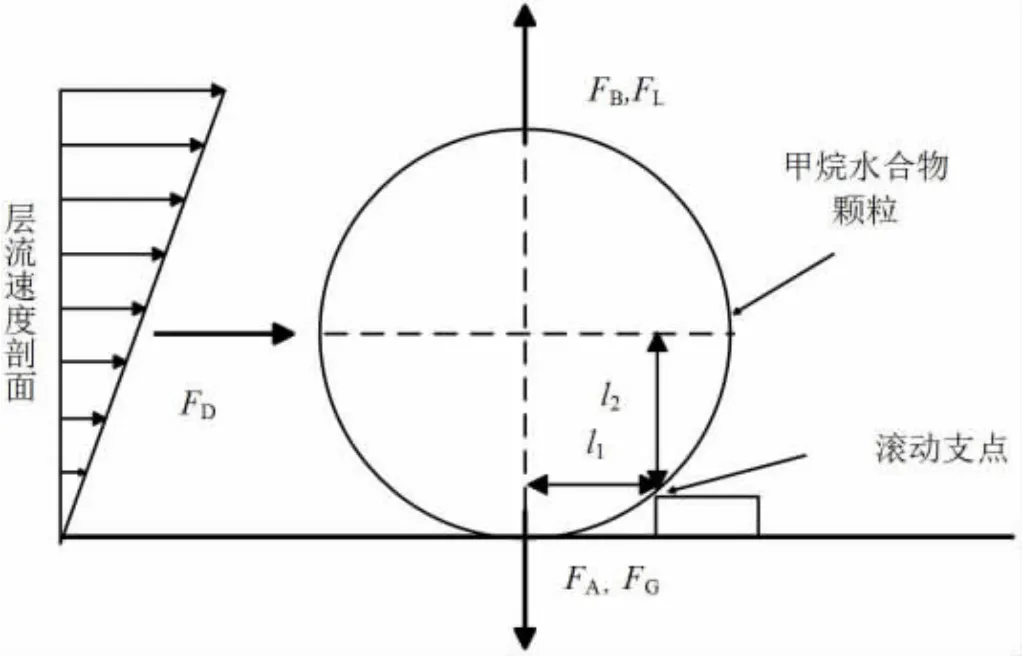
圖2 水合物顆粒在管壁上的應力狀態示意圖

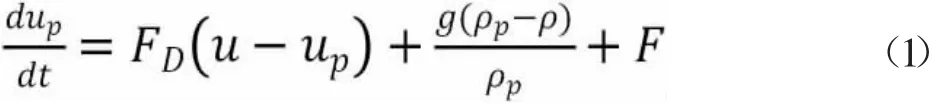
阻力FD可以通過公式（2）計算[8]。

當顆粒在近壁面移動時，流場變化以及壁面與顆粒間相互作用使顆粒受到薩夫曼升力和壁面粘附力的影響。由于壁面附近的流體速度梯度大，薩夫曼升力將對粒子運動產生很大影響，可通過下式[9]計算。

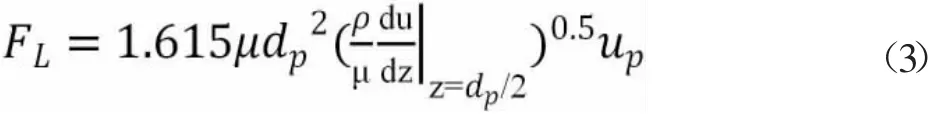
顆粒與壁面間的粘附力是兩個物體之間所有分子和原子吸引力的總和，計算方法見下式[9]。

先前的研究發現，顆粒旋轉是水合物顆粒沉積在壁上的關鍵因素。G.M.Burdick等人通過引入臨界顆粒雷諾數，定量表征了水合物顆粒在壁上的運動特性[10]。如果雷諾數大于臨界值，粒子將離開壁面。所建立的水合物顆粒沉積判斷標準如下式：

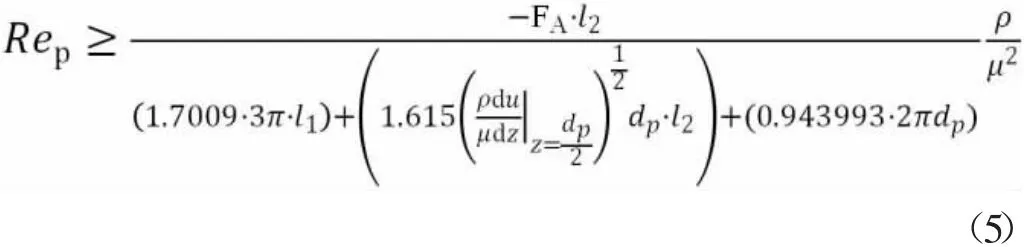
2 數值求解過程及結果分析

2.1 模擬方法和參數

模擬中使用的物理模型是長度為1.5m、直徑為0.1m的圓柱形管道。網格采用O-grid網格法劃分。氣體成分為純甲烷，液體含量為5%，氣體流速為15m/s，液體流速為0.08m/s。本研究采用瞬態模擬，使用歐拉-拉格朗日方法。由于顆粒的湍流擴散對顆粒軌跡方程的求解有很大影響，因此在該模擬中考慮了顆粒對連續相的影響。首先，利用k-ε模型得到收斂的連續相流場，然后建立離散相模型進行耦合計算。

2.2 結果和分析

本節以管徑0.15m，氣速15m/s，粒徑0.3mm模擬結果為例，對模擬結果進行分析。圖3為不同氣體速度下水合物沿管道軸向的濃度分布，水合物顆粒濃度主要集中在管道后部，最大顆粒濃度集中在管道底部。這是因為顆粒在管流中的徑向運動主要受重力的影響。同時，氣速越大，氣體對水合物顆粒施加的剪切力越強，因此水合物顆粒在壁上的濃度分布越小，水合物顆粒分布也越均勻。

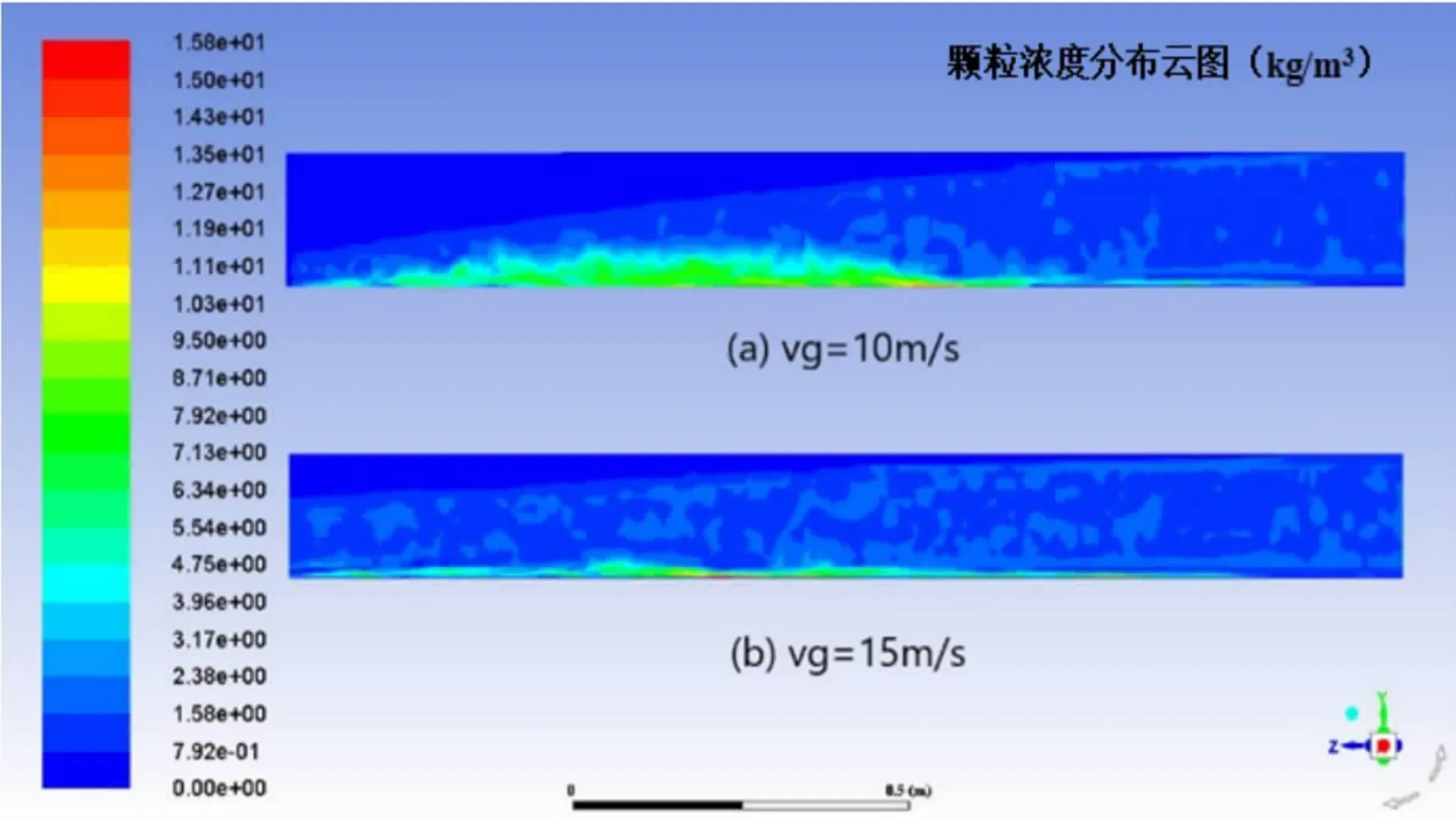
圖3 不同氣體速度下的顆粒濃度分布

通過捕獲壁面上的水合物顆粒，我們獲得了注入的顆粒總數和沉積在管壁上的顆粒數量，并計算了氣相中水合物顆粒的沉積率。圖4為不同氣速條件下水合物顆粒沉積率的結果。最大顆粒沉積率可以達到7%左右，沉積率隨氣體速度的增加而減小，隨顆粒尺寸的增加而增加。氣速對沉積率的影響體現在兩個方面。隨著氣速增加，流體湍動能越大，顆粒獲得的動能增大，使得顆粒的反彈能量更大，因此碰撞后沉積的概率降低；同時氣體的剪切效應更強，壁面顆粒在剪切力的作用下更容易返回氣流，導致沉積概率降低。

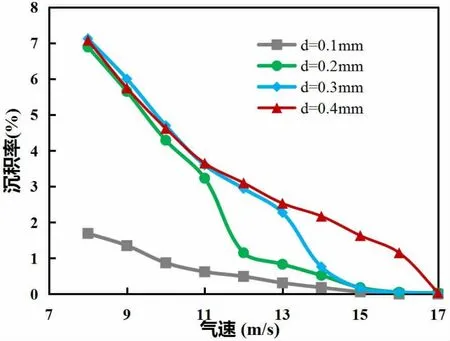
圖4 顆粒沉積速率隨氣體速度和顆粒尺寸的變化曲線

圖5表示了不同管徑不同粒徑水合物顆粒沉積率的變化曲線。粒徑較小時，沉積率的變化較大：粒徑增大，沉積率明顯增大；當粒徑增大到臨界值時，粒徑增大，沉積率幾乎穩定。在湍流核心區，顆粒的徑向運動主要受重力的影響，重力隨粒徑增大而增大，氣流對顆粒的攜帶作用減小，顆粒碰撞壁面的數量增加。對于微細顆粒，其壁面的粘附力為其他作用力數量級的幾倍，顆粒一旦附著在管壁便很難脫離；而對于大顆粒，由于壁面的粘附力與粒徑呈一次方關系，使顆粒脫離的作用力與粒徑呈三次方關系，因此顆粒粒徑越大，越容易從壁面脫離。因此，當顆粒為小粒徑時，粒徑越大，運動到壁面的顆粒數越多且易沉積，沉積率會增大；當粒徑增大到一定程度，雖然運動到壁面的顆粒數多，但是顆粒二次懸浮的量也會增大，最終會達到一個動態平衡，即粒徑增大，沉積率變化幅度不大。

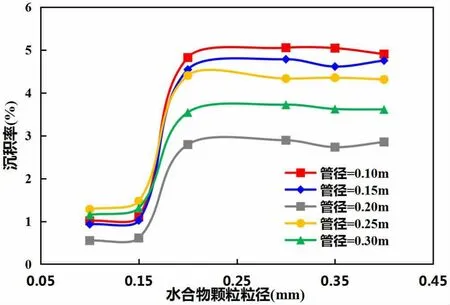
圖5 不同管徑下水合物顆粒沉積率隨粒徑變化曲線

3 結論

本文根據水合物顆粒的受力特性，建立了水合物顆粒運移模型和管壁沉積判斷準則，并在Fluent中對傳統的DPM模型進行了優化，得到了管道中的流場分布和水合物顆粒分布規律，并求解了不同氣速、顆粒粒徑及管徑條件下水合物顆粒沉積率。研究發現，水合物顆粒的運移速度主要表現為氣芯內的高速和管壁附近的低速，其運移主要受重力影響。同時氣核中水合物顆粒的沉積率約7%，隨著氣體速度的增加而降低，隨著顆粒尺寸的增加表現為先增大后穩定。本研究為準確預測水合物層的生長速度提供了理論依據。

注：

u，up—流體和顆粒速度，m/s；

g—重力加速度，m/s2；

ρp，ρ—顆粒和流體密度，kg/m3；

FD，FL，FA，FG，FB—阻力、Saffman升力、粘附力、重力、浮力，N；

AhmHamaker常數，本文取9.722×10-21；

h—顆粒與管壁間距，本文取14A；

l1，l2—顆粒旋轉力臂，m；

μ—動力粘度，N·s/m2；

dp—顆粒粒徑，mm；

CD—阻力系數；

Rep—顆粒雷諾數。