基于LASSO回歸的 R-vine copula 模型構建及其在化工過程故障檢測中的應用
鄧紅濤,賈 瓊,李紹軍,李 偉
(1.石河子大學,新疆 石河子 832000;2.華東理工大學 化工過程先進控制和優化技術教育部重點實驗室,上海 200237)
過程安全和產品質量是目前化工過程被關注最多的兩個問題,而過程監控是提高過程安全和產品質量的重要手段。隨著集散控制和數據采集系統的廣泛應用,工業過程采集數據的維度和數據量不斷增加,導致基于經驗知識和解析模型的方法在工業過程監控領域的研究受到了限制[1]。基于數據驅動的故障監控建模方法通過統計與分析過程數據來挖掘系統的特性,在描述未知機理模型和缺乏過程知識的復雜過程問題研究中備受學術和工業界關注。傳統的數據分析方法有偏最小二乘法(PLS)[2]和主元分析法(PCA)[3],這兩種方法適合分析具有線性、高斯分布特性數據。而處理非線性數據時常使用核方法來對這兩種方法進行改進,進而形成核偏最小二乘(KPLS)法[4]、核主元分析(KPCA)法[5]等。這些方法主要是基于降維的方式將高維數據映射到低維特征空間,消除變量間的相關性,但在降維過程中數據攜帶信息量都會有一定的損失。
近年來,針對復雜數據的相關性研究中,copula理論得到了廣泛的應用,將聯合概率分布函數與邊緣概率分布函數之間的相關性結構建立聯系。由于多變量copula在構建維數較大的數據間的依賴性時缺乏靈活性,Joe[6]提出了pair-copula,該方法是將多變量copula用一系列的二元copula來表示,該方法在刻畫高維數據的條件相關性、非對稱性、尾部相關性等方面均體現出更大的靈活性,已經在金融、環境、工程等領域得到了廣泛的應用。2015年Ren等[7]首先將vine copula函數引入到化工過程監控領域,提出了基于vine copula 相關性描述的多模態故障檢測方法。Zheng等[8]利用D-vine copulas 混合模型實現了對復雜的工業過程監控。周南等[9]利用核密度估計法構建 R-vine copula 結構并用在工業過程故障檢測中。由于二元copula函數類型眾多,vine copula結構矩陣不固定,選取合適的vine copula結構矩陣和copula函數類型成為建模的關鍵環節。目前常規方法是利用貪婪算法計算所有可能矩陣結構下變量之間的相關關系,選擇相關性最大的矩陣結構,然后根據赤池準則(AIC)選取copula函數類型和參數[10-12]。這種方法在處理高維的工業過程數據時,會出現計算量大、計算時間長的問題,其解也不能保證接近該高維組合優化問題的最優解。
筆者在構建R-vine copula模型時引入LASSO回歸來統計變量之間的相關關系,根據變量間聯系的強弱程度確定變量在R-vine矩陣中的位置,利用回歸分析正則化路徑選擇R-vine copula矩陣結構。遵循R-vine矩陣構建規則和回歸過程中懲罰力度調整變量在矩陣中的位置,確定R-vine結構矩陣模型,以獲得一個與變量獨立性有關的稀疏矩陣模型。該方法構建的矩陣結構獨立于copula函數類型和參數,在處理高維度復雜工業過程數據時,利用稀疏模型和懲罰力度簡化copula函數類型選擇過程,縮短了建模時間,使統計建模具有更強的靈活性。該方法應用在TE(Tennessee Eastman)過程中表現出較好的檢測效果。
1 R-vine copula 理論基礎和LASSO回歸
1959年Sklar第一次提出用copula函數分析復雜變量間的相關關系,將多維變量的聯合分布函數用邊緣分布函數和copula函數表示,但是這種copula函數面對高維數據時會出現參數過多而導致優化困難的問題[11]。1996年Joe[6]提出了vine copula結構。Vine copula結構分解具有較大的靈活性,分解策略較多[13-14]。2002年Bedford等[15]定義了R-vine copula 結構分解模型,相應的多元分布結構稱為R-vine結構,可以更加靈活地表達變量之間的關系[16]。
1.1 構建R-vine結構矩陣規則
用樹結構來表示vine結構,對于n維變量的R-vine分布,包含了n-1棵樹,每棵樹由節點和邊組成。兩個節點確定一條邊,每條邊用二元copula函數表示。由于vine copula結構分解模型多樣,樹型結構不唯一。為了更好地表示vine copula的結構,2013年Brechmann等[17]研究了一種R-vine copula結構模型,利用一個下三角矩陣M來表示R-vine分解模型,用矩陣M可以簡單地表示出R-vine 結構中的樹集T、節點集V和邊集E。
對一個n維變量的vine copula結構,可以用一個n×n的下三角矩陣M表示,矩陣對角線元素m代表變量X={x1,x2,…,xn}中的xm。用mi,j表示第i行第j列矩陣元素,mi,j∈{1,2,…,n},i=(1,2,…,n),j=(1,2,…,i)。矩陣元素之間需要滿足以下條件:
1){mj,j,…,mn,j}?{mi,i,…,mn,i},1≤i 2)mj,j?{mi,i,…,mn,i},1≤j 3){mi,j,{mi+1,j,…,mn,j}}?{mk,k,{mw,k,…,mn,k}}。即如果矩陣元素集Q={mi,j,{mi+1,j,…,mn,j}},j=(1,2…,n-2),i=(j+1,…,n),那么一定存在包含或等于Q的元素集{mk,k,{mw,k,…,mn,k}},j 設滿足以上規則的矩陣M中第i行第j列元素m集合為W。 根據以上條件可以發現矩陣中元素位置是互相約束的,如圖1所示矩陣M,組成第2列的變量{4,2,1,3}包含在第1列{5,2,1,3,4}中;第2列對角線元素{4}不會出現在第3、4、5列中;第1列畫圈元素組成元素集Q={3,4},那么至少第2列中存在包含Q的元素集{4,1,3}。 圖1 5維變量的R-vine矩陣M 假設畫圈元素m4,1為O,O和第1列中行數大于4的元素組成元素集Q={O,4}。列數大于1、行數大于等于4的元素和對角線元素(帶上橫線元素)組成的元素個數大于等于Q的元素集{4,1,3}、{3,2,1}、{2,1},這些元素集中包含元素4的只有{4,1,3},根據條件3可知畫圈位置的元素O只能在變量集W={3,1}中選取。 利用R-vine的矩陣結構,不需要畫樹結構就可以快捷地表示出多維變量的聯合密度函數[18]。矩陣元素mi,j和第j列元素可以表示樹Tn-i+1的第i-j+1個二元copula函數cj(e),k(e)|D(e)(Fj|D(xj(e)|xD(e)),Fk|D(xk(e)|xD(e))),其中j(e)=mj,j,k(e)=mi,j,D(e)={mi+1,j,…,mn,j},i=(2,3,…,n),j=(1,2,…,i-1),F為條件累計分布函數。 n維變量的聯合概率密度P可以表示為邊緣概率密度f(xi)與copula密度函數c的乘積形式: (1) 式中:fi(xi)為第i個變量xi的邊緣概率密度函數,cmj,j,mi,j|mi+1,j,…,mn,j為二元copula函數,F(xmj,j|xmi+1,j:mn,j)為xmj,j的條件累計分布函數。 圖1所示矩陣M為R-vine結構矩陣,矩陣中元素m的值1-5代表變量X={X1,X2,X3,X4,X5}。矩陣M中畫圈元素m4,1=3,對應二元copula為:c3,5|4,變量m1,1條件密度可以用第1列所有元素的二元copula函數之積和對角線元素的邊緣密度表示: f(x5|x1x2x3x4)=f(x5)c4,5c3,5|4c1,5|3,4c2,5|1,3,4。 (2) 聯合概率密度為: f(x1,x2,x3,x4,x5)=f(x1)f(x2|x1)×f(x3|x1x2)f(x4|x1x2x3)f(x5|x1x2x3x4)。 (3) 根據矩陣M求5維變量聯合概率密度,即: f(x1,x2,x3,x4,x5)=f(x1)f(x2)f(x3)f(x4)f(x5)×c1,2c1,3c3,4c4,5c2,3|1c1,4|3c3,5|4c2,4|1,3c1,5|3,4c2,5|1,3,4。 (4) 在滿足矩陣規則的前提下構造合理的R-vine結構矩陣M是構建R-vine copula模型的關鍵[19]。目前常用貪婪算法構建R-vine樹的結構矩陣,計算樹節點之間的相關性,按照最強相依性原則遍歷所有可能的矩陣結構,尋找最大相關系數之和以構建R-vine結構矩陣,并在整個結構選擇過程中迭代擬合copula函數及其參數。此方法計算時間長,計算量大,構建的模型結構復雜,容易出現過擬合現象。 線性回歸表示變量間相互依賴的定量關系,變量x={x1,x2,…,xn}回歸函數如下: (5) 式中φm為變量xm的回歸系數。 LASSO回歸是一種數據降維方法,善于處理變量的篩選。1996年Tibshirani[20]首次在普通線性回歸模型中添加了懲罰項,通過改變懲罰項將一些作用比較小的變量線性系數壓縮,最終變為零,從而獲得稀疏解。這種基于懲罰方法對樣本數據進行變量選擇,防止了數據過擬合,不但可以用于線性關系,也可以用于非線性關系。回歸損失函數公式如下: (6) 式中:hφ(x(t))是根據式(5)計算預測第t個樣本的值,因變量y為真實樣本值,q為樣本個數,t=(1,2,…,q),λ為正則化參數,r為參數個數,k=(1,2,…,r)。隨著λ增大,各變量的系數逐漸趨于零。 將LASSO回歸算法用于構建R-vine結構矩陣,提出一種新的構建R-vine結構矩陣的方法[21]。如構建n維變量X={X1,X2,…,Xn}的R-vine結構矩陣M。 首先確定R-vine結構矩陣M中的對角線元素。將變量帶入式(7),按照式(6)利用交叉驗證方法確定過程變量xi(i=1,2,…,n)的LASSO回歸方程。 (7) 式中:m=1,2,…,n,z=1,2,…,n,且m≠z。根據式(8)統計n個回歸方程中變量xm的回歸系數φm,z非零的個數uz,按照uz的升序將變量xm設為R-vine結構矩陣M的對角線元素,當出現次數相同時按照回歸系數的和排序。 (8) 如圖1所示,矩陣M確定對角線元素時,存在u5≤u4≤u3≤u2≤u1,那么對角線元素為{5,4,3,2,1}。 接下來按照從右往左、從下至上的順序確定矩陣中的其他元素。如確定矩陣M中的變量mi,j,以矩陣對角線元素xmj,j為因變量y,根據R-vine結構矩陣構建規則,以滿足元素集W的元素為自變量,帶入式(5),根據式(9)利用最小回歸角方法選擇變量,當回歸系數依次置為零時,懲罰項最大的變量即為mi,j。 (9) 式中:W為根據R-vine矩陣規則確定的此處可放置的變量集合,l是屬于集合W的元素。 確定圖1中矩陣M第5行第4列的元素,根據R-vine矩陣規則可知m5,4=1,然后按照從右往左、從下至上的順序依次確定m5,3、m5,2、m5,1、m4,3、m4,2、m4,1、m3,2、m3,1、m2,1。確定畫圈元素m4,1時,根據構建R-vine結構矩陣規則推出可用變量W={1,3},則以m1,1為自變量y,以m4,2和m5,5為因變量,按照式(5)利用LASSO回歸計算回歸系數,按照式(9)利用最小回歸角方法調整懲罰項。當φ1=0時λ=λ1;φ3=0時λ=λ3。因為存在λ1<λ3,那么m4,1=3。 本研究中利用LASSO回歸過程反映變量之間關系的特點,按照變量回歸系數歸零速度和懲罰項大小確定R-vine結構矩陣M,利用正常樣本數據根據赤池準則確定R-vine copula模型中參數,構建模型,利用閾值法進行在線故障檢測(如圖2所示)。 圖2 LRVC過程監控方法示意圖 1)獲得正常操作過程的訓練樣本集,按照第2節方法構建R-vine矩陣M。 2)根據R-vine矩陣M確定copula對和參數,構建R-vine copula模型。合適的copula對能夠精確地描述變量數據間的相關關系。采用基于似然函數的赤池信息準則[23]選取最合適copula對類型。赤池準則是權衡被估計模型復雜度和擬合優越性的一種標準,其定義如下: (10) 3)確定檢測閾值T。 計算樣本點的聯合概率密度,利用分位數法[7]求對應的聯合概率密度中閾值T。該方法根據高密度區域與密度分位數理論構建廣義貝葉斯推斷概率指標(GLP),閾值T選取99%的控制限,監測時對比靜態密度分位數表確定監測狀態。 1)利用模型計算監測數據聯合概率密度函數。 2)以閾值T為界限,小于閾值則為故障數據。 Eastman 公司依照實際的化工反應過程開發了TE測試平臺,仿真數據具有非線性、時變和強耦合性等特征,能很好地模擬復雜工業過程,被廣泛應用于控制、優化、過程監控與故障診斷的研究。TE數據集由訓練集和測試集構成,數據集包含了正常狀態數據和21種故障狀態數據,每個樣本都有52個觀測變量,其中連續變量22個,操縱變量12個和成分變量19個。本研究所用數據可從http:∥web.mit.edu/braatzgroup/links.html下載,在離線狀態下選取了正常工況下樣本52個變量中的22個連續的過程變量構建R-vine copula模型,采用960個正常樣本點來建立模型,每種故障狀態的測試數據也選用960個樣本點進行測試,對21個故障數據進行監測。將本研究中提出的方法LRVC與獨立成分分析(ICA)、高斯混合模型(FGMM)、R-vine copula(RVC)等算法計算TE過程故障檢測率進行比較,結果見表1,其中T2和SPE是ICA故障檢測的統計指標,T2指標衡量樣本向量在主元空間的變化,SPE指標衡量樣本向量在殘差空間的投影的變化,BIP是貝葉斯推理的后驗概率(BIP)指標,FT指利用RVC模型和LRVC模型下的廣義貝葉斯推斷概率指標。表中粗體表示檢測效果最好的值。 表1 TE過程故障檢測率對比表 可以看出利用LASSO回歸構建的R-vine模型監測結果優于貪婪算法構建R-vine矩陣建模,與FGMM、ICA方法[23-24]比較具有較高的檢測率。LRVC模型的故障檢測率都略高于利用貪婪算法構建矩陣的模型檢測率,在故障2、4~9、12、16、20中都表現出較好的檢測效果,其他故障的檢測效果和其他方法相差不多。LRVC模型有13類故障的檢測率都高于FGMM方法的檢測結果,相比于ICA檢測方法在故障2、4、5、7、9、12、20中都表現較好檢測率。 TE過程中數據具有非高斯態的特性,FGMM方法是基于馬氏距離判斷數據是否異常,反映數據的非高斯特性能力較差;ICA方法在數據變換和特征提取的過程中會造成部分信息的損失。而LRVC方法利用LASSO回歸建立R-vine矩陣構建模型,全面挖掘出數據變量之間的信息,在刻畫非高斯、非線性方面有顯著的優勢,提高了故障檢測的性能。圖3為LRVC方法對故障8和故障12的監控圖,橫坐標為對聯合概率密度P取對數。 圖3 TE過程故障 8、12的LRVC監控圖 醋酸脫水過程控制系統包括4個進料和90級塔板,用于建模的300組測試數據和500組訓練數據來自分布式控制系統(DCS),包括溫度、流量、壓力等連續的21個監測變量。表2為核主元分析KPCA、FGMM、和LRVC 3種方法的檢測率(fault detection rate,FDR)和誤報率(false positive rate,FPR),可見LRVC方法在醋酸脫水過程監測中表現較好。 表2 醋酸脫水過程檢測率和誤報率 提出了一種基于LASSO回歸構建 R-vine copula 模型的化工過程故障檢測方法LRVC,與傳統方法相比具有較好的檢測效果。LRVC模型利用LASSO回歸過程反映變量之間相關性的特性,依據回歸過程懲罰力度構建R-vine矩陣,采用赤池準則進行copula類型選擇構建R-vine copula模型。模型中利用LASSO回歸統計多元變量相關性構建R-vine矩陣更能體現vine copula結構分解特性,適合高維變量數據分析。基于LRVC模型的過程故障檢測方法充分利用了copula函數可以反映變量之間非高斯、非線性的特性,在不降維的情況下直接描述變量之間關系,具有更好的解釋能力和適應性。此方法簡化了構建R-vine矩陣過程,在超高維變量的建模過程中可以直接利用矩陣進行copula函數的選擇,節省了建模時間。該方法在TE過程以及醋酸脫水過程中的應用表明其在工業過程故障檢測中具有應用前景。
1.2 利用矩陣M表示聯合密度函數
1.3 LASSO回歸
2 利用LASSO回歸構建R-vine矩陣
3 基于LASSO構建R-vine copula模型的故障檢測方法
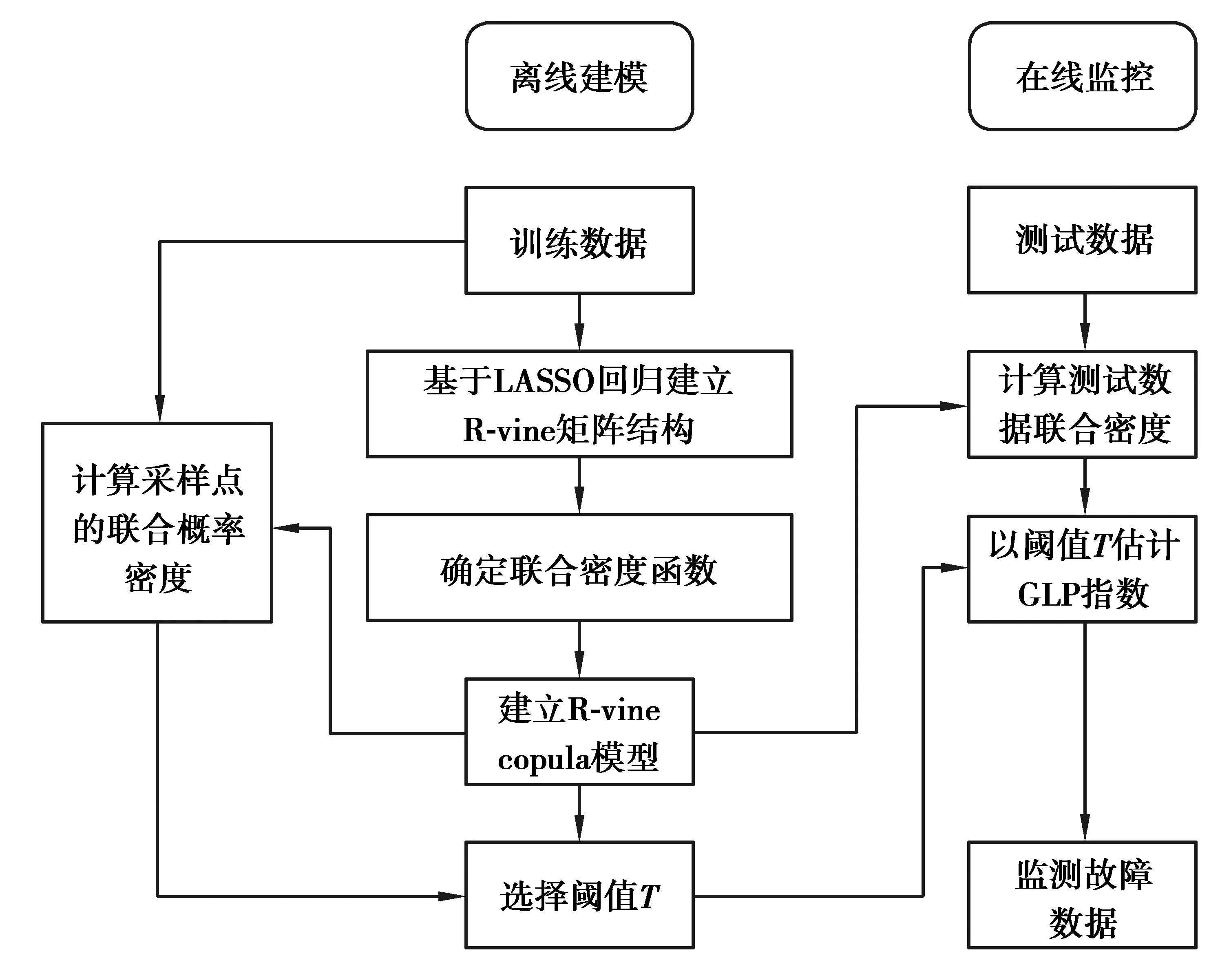
3.1 離線建模

3.2 在線監控
4 應用分析
4.1 TE過程
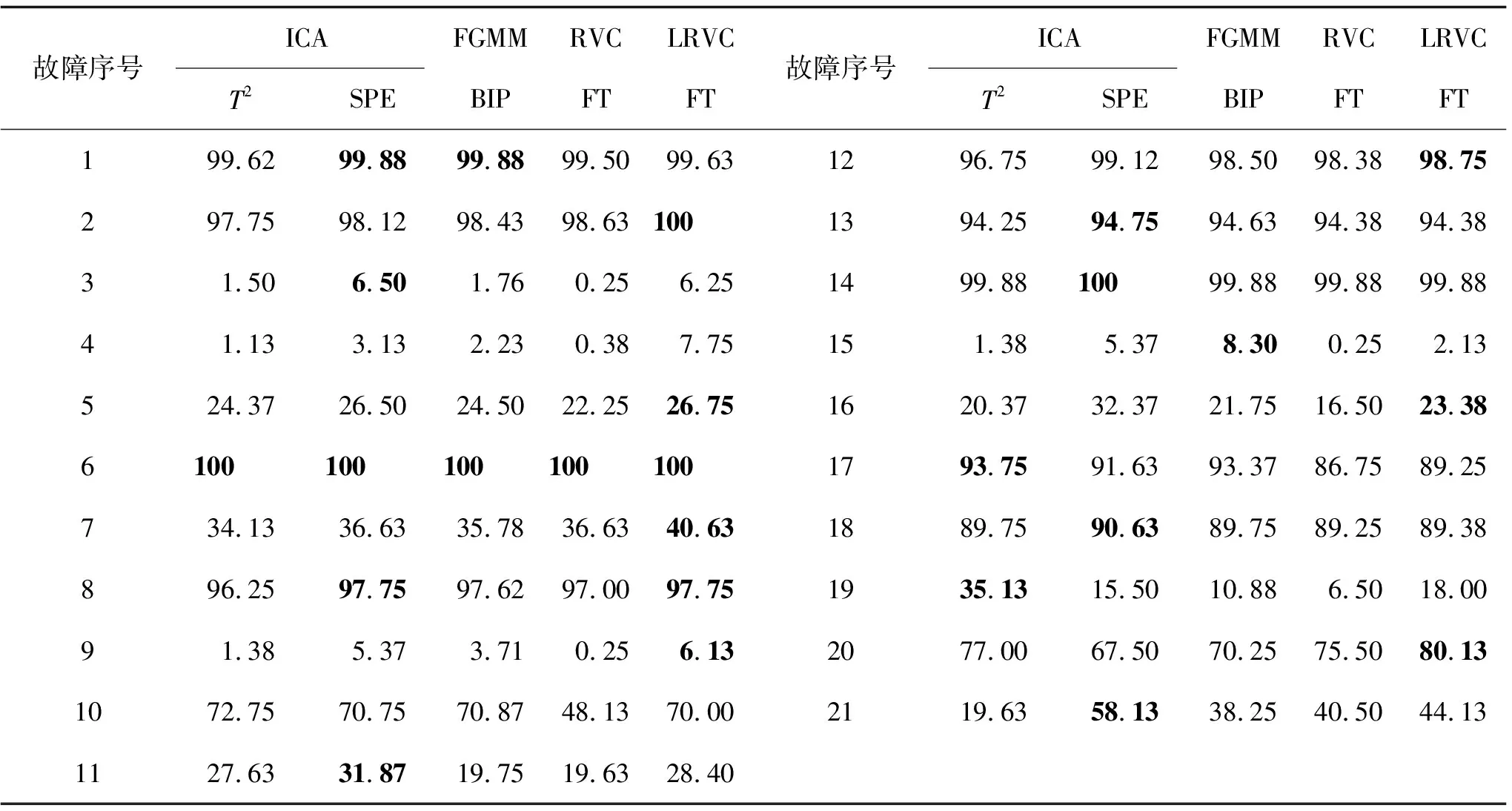

4.2 醋酸脫水過程

5 結 論

