近斷層地震作用下設備-結構耦合隔震體系動力響應分析

韓 淼, 蔣金衛, 杜紅凱, 劉洋博, 馮思嘉, 董凱旗

(北京建筑大學北京未來城市設計高精尖創新中心, 北京 100044)

0 引言

非結構構件分為持久性的非結構構件和支撐于建筑結構的附屬設備[1]。隨著經濟的發展和人們對生活環境要求的提高,非結構構件的造價提升,在有些建筑中甚至已超過結構構件[2-3],若在地震中發生破壞,將造成不可估量的經濟損失和人員傷亡。建筑主體結構與附屬設備等非結構構件是耦合的結構整體,當設備質量較大時,兩者的相互作用不應忽略。關于設備與傳統抗震結構的耦合作用已有較多研究:李杰等[4-5]通過建立1∶4縮尺的多種不同類型結構體系進行振動臺試驗,研究表明設備與結構的耦合關系對設備-結構耦合體系的頻譜特性有顯著影響;林均岐[6]通過振動臺試驗模擬位于樓層頂部不同的非結構構件對整體結構響應的影響,結果表明非結構構件質量比和阻尼比的變化對整體結構的動力響應存在明顯影響;陳建兵等[7]提出通過場地土的卓越周期判定設備與結構的相互動力作用對設備-結構耦合體系的動力響應影響。

自1994年Northridge地震和1995年Kobe地震后,國內外學者發現近斷層地震動對長周期結構的破壞較大[8],尤其是具有脈沖特性的近斷層地震動[9-10]。隔震技術因具有延長結構自振周期的特點,能達到保護上部結構的目的,近年來得到廣泛應用。因此,諸多學者對近斷層地震動作用下的隔震結構響應進行了深入研究[11-13],但多關注于無設備耦合的隔震結構響應,關于近斷層地震動作用下設備與隔震結構耦合體系的動力響應研究較少。

據此,本文基于現有振動臺試驗數據的初步結論,選取近斷層脈沖型和非脈沖型地震動各50條,對振動臺試驗模型進行模擬分析,研究設備-結構耦合隔震體系的動力響應。

1 結構分析模型建立

以某5層鋼框架結構為例進行研究,其設防烈度為8度(0.2g),場地類別Ⅱ類,設計地震分組為第一組,框架層高3.6 m,縱、橫向均為6跨,跨度7.2 m,如圖1所示。為開展振動臺模型試驗,考慮到振動臺臺面尺寸的限制,將該5層鋼框架結構進行等效簡化,得到雙向單跨原型結構,并制作1∶4縮尺模型。梁、柱均采用方鋼管,截面尺寸分別為70 mm(高)×70 mm(寬)×6 mm(厚)和100 mm(高)×100 mm(寬)×5 mm(厚),鋼材采用Q355鋼。樓板采用10 mm厚的鋼板,樓層配重:1～4層2 040 kg,5層2 268 kg。模型的相似關系如表1所列。

圖1 5層鋼框架結構Fig.1 Five-story steel frame structure

表1 模型的相似關系

雙向單跨原型結構與其縮尺模型的前3階自振周期如表2所列。將縮尺模型的自振周期根據時間相似比1∶2轉換后與原型結構周期進行對比,誤差<3%,滿足計算精度要求。

表2 原型結構與縮尺模型前3階自振周期(單位:s)

在每根柱下安裝一個橡膠隔震支座,支座水平剛度為0.25 kN/mm,其他參數如表3所列。在縮尺模型頂層耦合一個由4根長400 mm、直徑12 mm的圓鋼連接而成的設備。圓鋼間距250 mm,設備質量為200 kg,自振頻率為3.95 Hz,組成設備-結構耦合隔震體系。利用ABAQUS有限元軟件進行建模,梁柱采用B32梁單元,樓板選用S4R5殼單元(圖2)。耦合隔震體系的基本周期為0.85 s。

2 地震波選取

從太平洋地震工程研究中心(PEER)數據庫中選取100條典型近斷層地震波,其中近斷層脈沖型和非脈沖型地震波各50條。脈沖型地震波按脈沖周期升序排列,非脈沖型地震波按峰值位移(Peak Ground Displacement,PGD)升序排列。選波原則如下:

表3 支座參數(單位:mm)

圖2 有限元分析模型Fig.2 Finite element calculation model

(1) 根據國內外大多數研究學者公認的近斷層地震動斷層距定義,選取斷層距在20 km以內的地震波;

(2) 為突出近斷層地震異于遠場地震動的強度特征,選擇矩震級不小于5.5級的地震波;

(3) 為突出近斷層地震動的強地面運動特性,選擇峰值加速度大于0.1g的地震波；

(4) 地震波是否具有脈沖以及脈沖周期數值根據PEER數據庫確定[14]。

3 耦合隔震體系動力響應分析

將選取的近斷層脈沖型和非脈沖型地震波的峰值加速度(Peak Ground Acceleration,PGA)調幅至0.07g、0.20g和0.40g,依次對應設防烈度8度(0.2g)的小震、中震和大震,分組輸入給設備-結構耦合隔震體系模型,對耦合隔震體系的隔震層位移、層間位移、樓層加速度、設備加速度等動力響應進行分析,研究近斷層脈沖型和非脈沖型地震動對設備-結構耦合隔震體系動力響應的影響。

3.1 隔震層位移響應

圖3(a)、(b)、(c)分別繪出了PGA為0.07g、0.20g、0.40g時,50條脈沖型和50條非脈沖型地震波作用下隔震層的位移最大值，圖中P1代表脈沖型地震作用的位移最大值,NP1代表非脈沖型地震作用的位移最大值。從圖3中可看到,近斷層脈沖型地震作用下的隔震層位移總體上大于非脈沖型地震作用；隔震層位移的最大值為98.39 mm(40號脈沖地震波),超出橡膠隔震支座水平方向變形的限值，即隔震支座有效直徑150 mm的0.55倍和隔震支座橡膠總厚度3倍之間的較小值82.5 mm。

表4給出了近斷層脈沖型和非脈沖型地震作用下隔震層位移的最大值、平均值對比。從表4中可看到,近斷層脈沖型和非脈沖型地震作用下的隔震層位移最大值之比約為2.49,平均值之比約為2.25。這說明耦合隔震體系的隔震層位移響應需考慮近斷層地震動脈沖特性的影響。

3.2 層間位移響應分析

圖4(a)、(b)、(c)分別繪出了PGA為0.07g、0.20g、0.40g時,近斷層脈沖型和非脈沖型地震作用下耦合隔震體系樓層層間位移的最大值與平均值曲線。圖中P2代表脈沖型地震作用的位移平均值,NP2代表非脈沖型地震作用的位移平均值。由圖4可看出,在近斷層脈沖型和非脈沖型地震作用下,樓層層間最大位移均呈反C形,1層與2層較大,3～5層逐漸減小。

表5給出了近斷層脈沖型和非脈沖型地震作用下耦合隔震體系樓層層間位移最大值、平均值的對比,同時在括號內給出了相應的層間位移角。從表5中可以看到,近斷層脈沖型和非脈沖型地震作用下耦合隔震體系層間位移的最大值之比約為2.25,平均值之比約為2.17。這說明耦合隔震體系的層間位移響應需考慮近斷層地震動脈沖特性的影響。

由《建筑抗震設計規范》[1]可知,多、高層鋼結構彈性層間位移角限值為1/250,彈塑性層間位移角限值為1/50。由表5可看到:

(1) 當PGA為0.07g時,近斷層脈沖型和非脈沖型地震作用下層間位移角平均值均遠小于1/250,即結構能保持彈性;僅1條脈沖型地震波的層間位移角大于1/250,占2%。

(2) 當PGA為0.20g時,脈沖型地震作用下層間位移角的平均值大于1/250，非脈沖型地震作用下層間位移角的平均值小于1/250,最大值大于1/250。層間位移角最大值大于1/250的地震波共38條,其中脈沖型地震動32條,占64%;非脈沖型地震動6條,占12%。近斷層非脈沖型地震作用下結構基本能保持彈性,但在脈沖型地震作用下結構進入彈塑性的概率明顯增加。

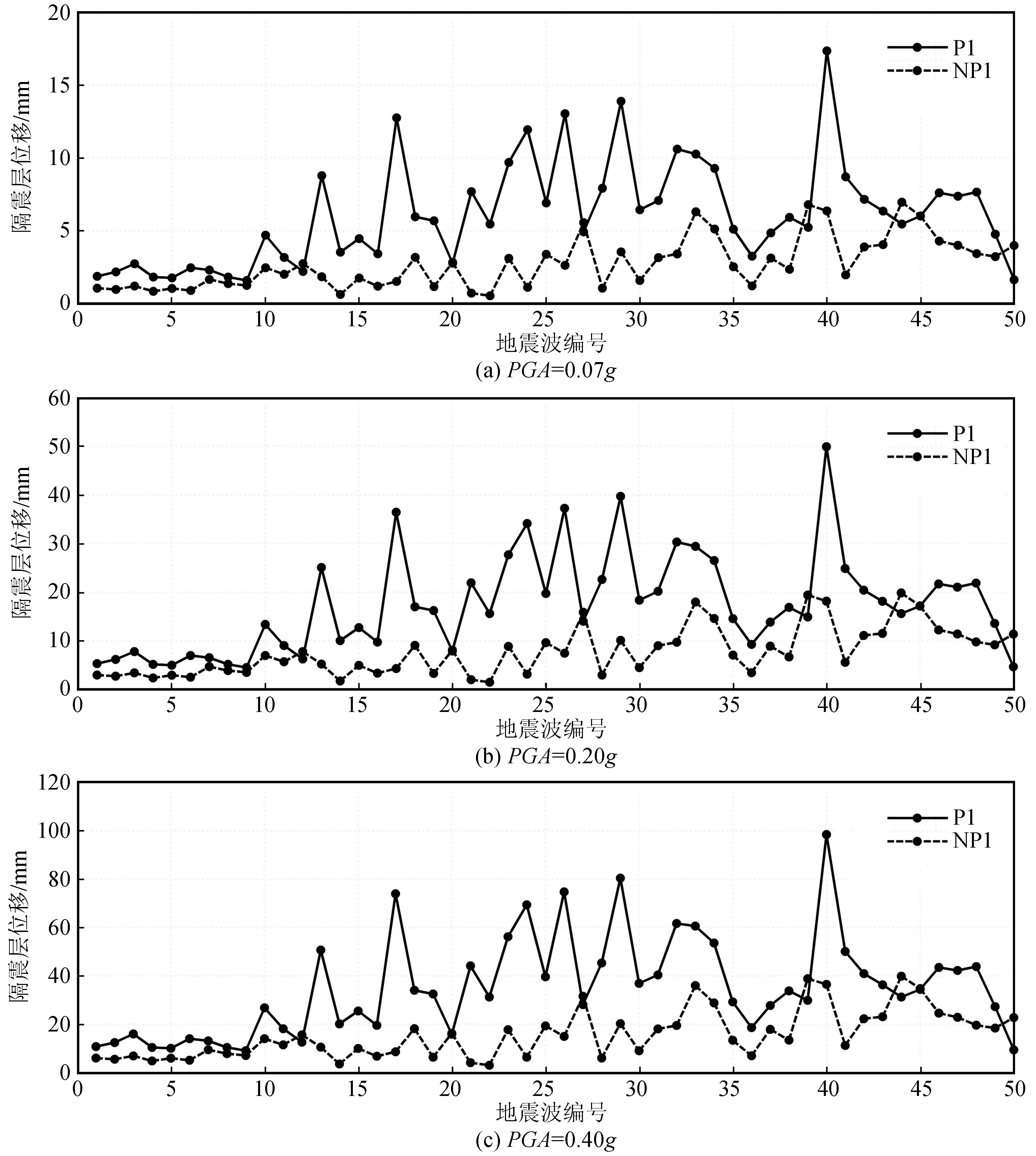
圖3 近斷層脈沖型和非脈沖型地震作用下的隔震層最大位移對比Fig.3 Comparison between the maximum displacement of isolation layer under near-fault pulse-like and non-pulse-like ground motions

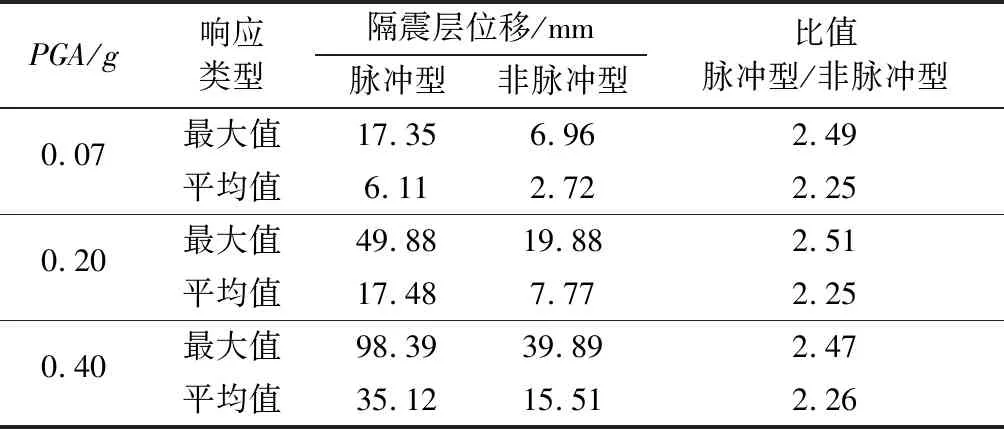
表4 隔震層位移對比

(3) 當PGA為0.40g時,近斷層脈沖型和非脈沖型地震作用下層間位移角的平均值均大于1/250。層間位移角最大值大于1/250的地震波共70條,其中脈沖型地震動45條,占90%;非脈沖型地震動25條,占50%。非脈沖型地震作用下結構進入彈塑性的概率已較大,在脈沖型地震作用下結構基本進入彈塑性,且超越彈塑性位移限值的概率為4%。

綜上可得,相比近斷層非脈沖型地震動,耦合隔震體系在近斷層脈沖型地震動作用下的表現較差,結構進入彈塑性的概率明顯增大。

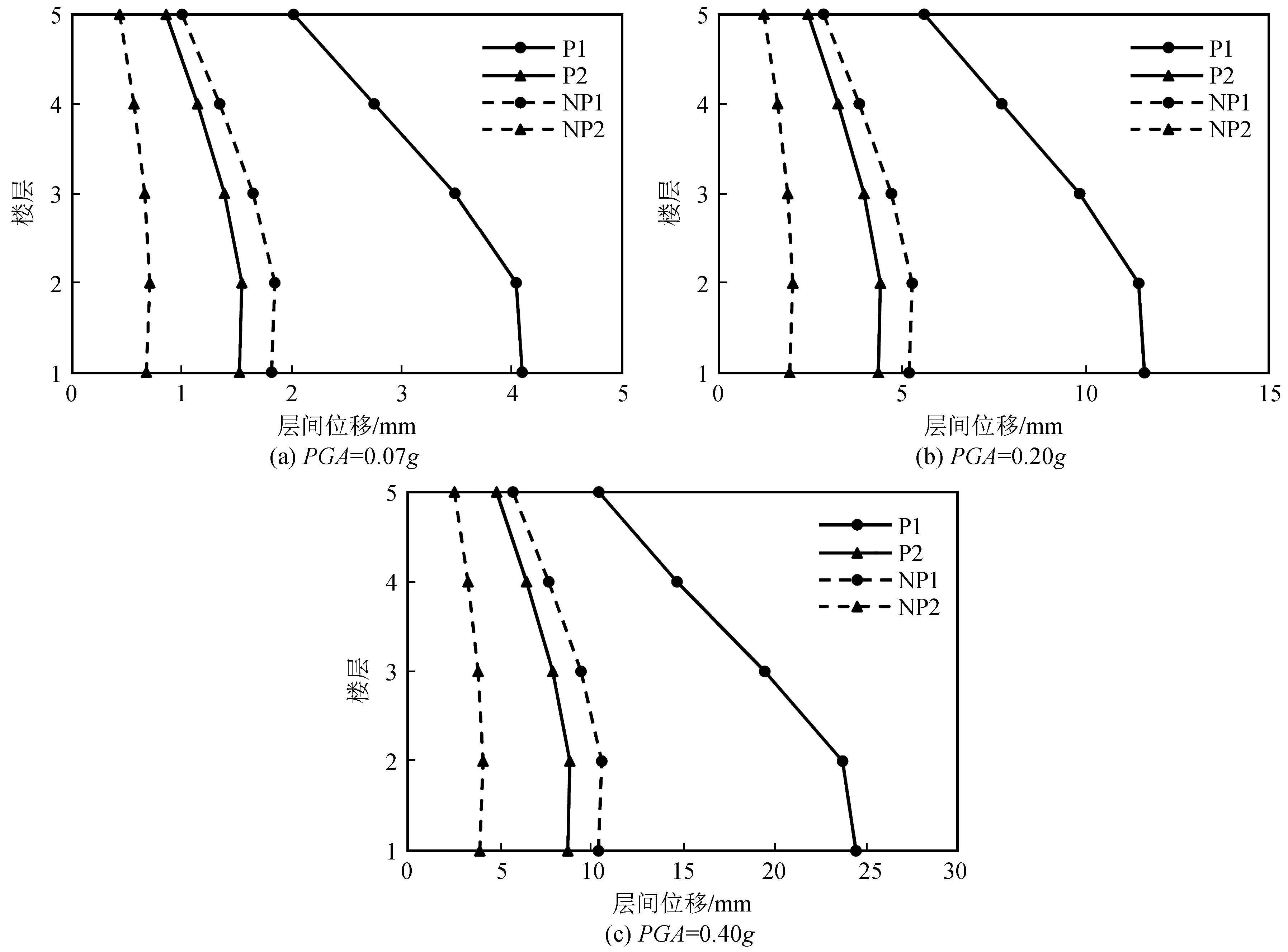
圖4 近斷層脈沖型和非脈沖型地震作用下的層間最大位移Fig.4 The maximum story drift under near-fault pulse-like and non-pulse-like ground motions

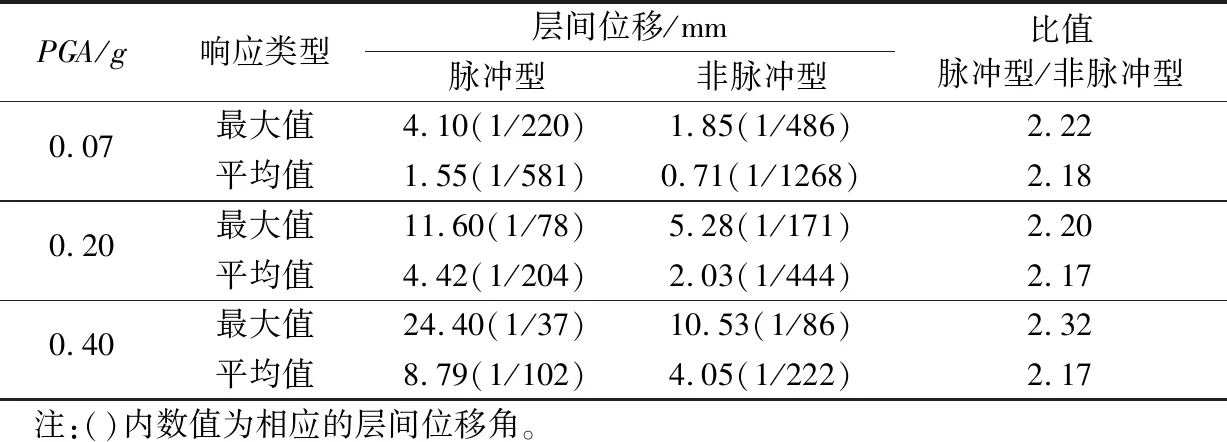
表5 層間位移對比

3.3 樓層加速度響應

圖5繪出了PGA分別為0.07g、0.20g、0.40g時,近斷層脈沖型和非脈沖型地震作用下樓層加速度的平均值曲線。由圖5可以看到,樓層加速度沿高度呈C形變化或隨高度的增加而增大,但以C形變化為主。其中,脈沖型地震作用下樓層加速度呈C形變化的比例為60%左右,非脈沖型地震作用下的比例為80%左右。一般而言,隔震技術可使頂層加速度峰值小于PGA[15],但由圖5可知,近斷層脈沖型地震動作用下耦合隔震體系的頂層加速度平均值大于PGA。

表6給出近斷層脈沖型和非脈沖型地震作用下樓層加速度最大值、平均值的對比。由表6可知,PGA為0.07g、0.20g、0.40g時,近斷層脈沖型和非脈沖型地震作用下耦合隔震體系的樓層加速度的最大值之比約為1.71,平均值之比約為2.24。樓層加速度通常作為加速度敏感型非結構構件的性能指標,故耦合隔震體系的樓層加速度響應需考慮近斷層地震動脈沖特性的影響。

3.4 設備加速度響應

圖6(a)、(b)、(c)分別繪出了PGA為0.07g、0.20g、0.40g時,50條脈沖型和50條非脈沖型地震動作用下頂層設備的加速度最大值。由圖6可知,近斷層脈沖型地震作用下的設備加速度總體上大于非脈沖型地震作用。

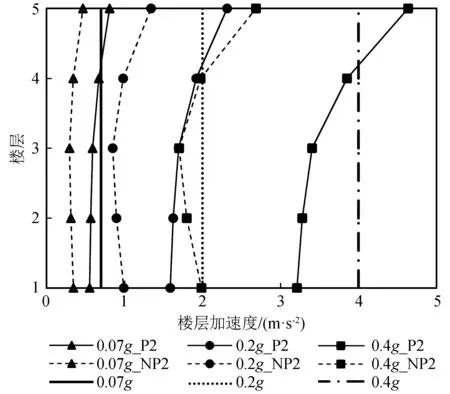
圖5 近斷層脈沖型和非脈沖型地震作用下的樓層加速度Fig.5 Floor acceleration under near-fault pulse-like and non-pulse-like ground motions

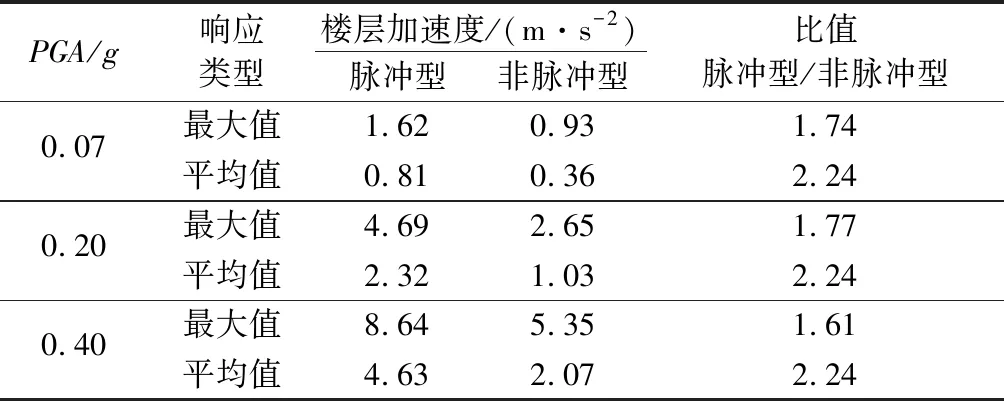
表6 樓層加速度對比

表7給出了近斷層脈沖型和非脈沖型地震作用下頂層設備加速度最大值、平均值的對比。由表7可知,近斷層脈沖型和非脈沖型地震作用下,設備加速度的最大值之比約為1.06,平均值之比約為1.17。這說明脈沖特性對設備-結構耦合隔震體系中的設備加速度具有一定影響,隔震設計時需加以考慮。

3.5 設備位移響應

圖7(a)、(b)、(c)分別繪出了PGA為0.07g、0.20g、0.40g時,50條脈沖型和50條非脈沖型地震動作用下頂層設備位移的最大值。表8給出了脈沖型和非脈沖型近斷層地震作用下,耦合隔震體系頂層設備位移最大值、平均值的對比。由圖7可知,33號脈沖型地震動作用下設備位移響應最劇烈;當PGA=0.40g時,設備塑性變形較大,時程曲線產生較大偏移,無法繞時間軸波動。由表8中PGA=0.40g時脈沖型和非脈沖型的設備位移比值明顯大于PGA=0.07g和PGA=0.20g時,亦可發現該現象。由表8可知,近斷層脈沖型和非脈沖型地震作用下設備位移平均值之比約為1.20,說明脈沖特性對設備-結構耦合隔震體系中的設備位移有影響,隔震設計時宜加以考慮。

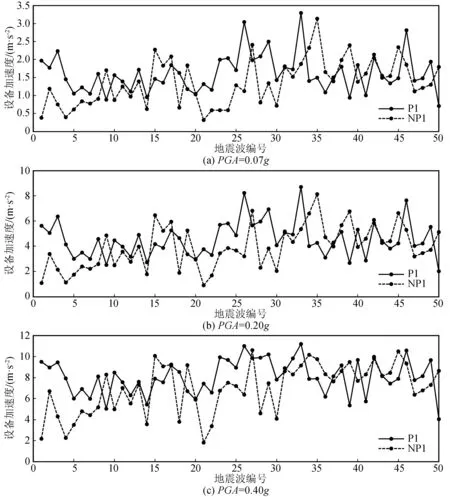
圖6 近斷層脈沖型和非脈沖型地震作用下設備加速度最大值對比Fig.6 Comparison between the maximum acceleration of equipment under near-fault pulse-like and non-pulse-like ground motions

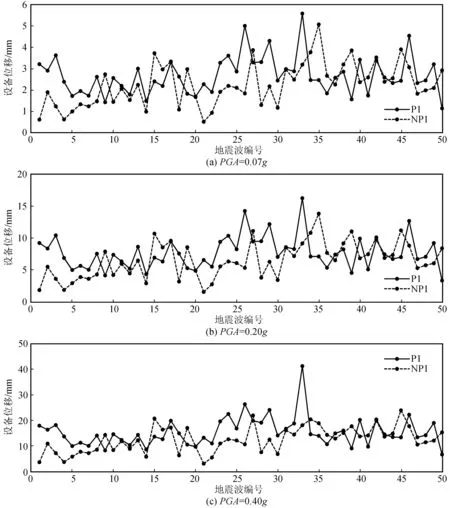
圖7 近斷層脈沖型和非脈沖型地震作用下設備位移最大值對比Fig.7 Comparison between the maximum displacement of equipment under near-fault pulse-like and non-pulse-like ground motions

表7 設備加速度對比

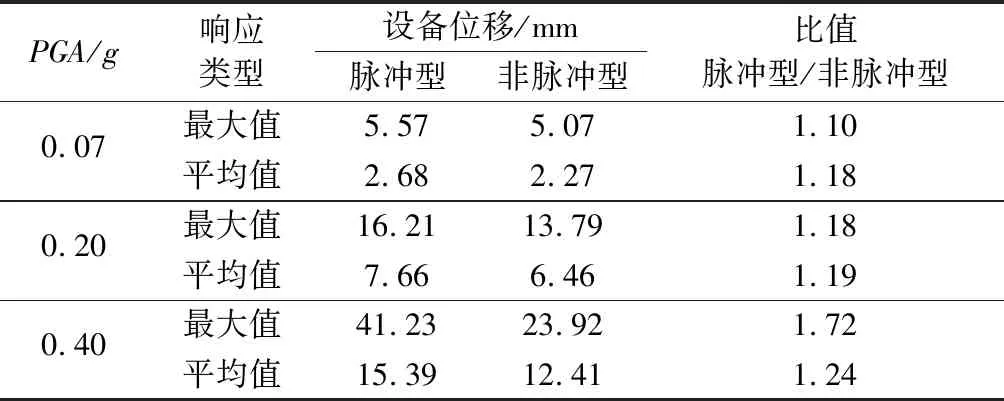
表8 設備位移對比

50條近斷層脈沖型地震波中,40號波引起了隔震層最大響應,33號波引起了設備最大響應;50條近斷層非脈沖型地震波中,引起隔震層和設備最大響應的地震波也不同。這表明近斷層地震動對耦合體系中主體結構和設備響應的影響有較大不同,引起主體結構最大響應的地震動對應的設備響應不一定最大,二者無絕對關系。對比響應的比值發現,脈沖特性對結構響應的影響明顯大于對設備響應的影響;脈沖型與非脈沖型地震動作用下,結構平均響應的比值>2,而設備平均響應的比值≤1.2。究其原因在于近斷層地震動中的脈沖具有低頻特性,對隔震主體結構響應的影響較大,而設備與主體結構之間存在耦合作用,導致近斷層脈沖型地震動作用下設備響應大于非脈沖型地震動,但設備頻率明顯大于主體結構頻率,屬于高頻,故脈沖對其響應的增幅相對較小。

4 結論

基于本文設備-結構耦合隔震體系,對近斷層脈沖型和非脈沖型地震作用下的隔震層位移、層間位移、樓層加速度、設備加速度以及設備位移響應進行分析,得到以下結論。

(1) 相比近斷層非脈沖型地震動,耦合隔震體系在近斷層脈沖型地震動作用下的表現較差:近斷層脈沖型地震作用下的隔震層位移、層間位移和樓層加速度明顯大于非脈沖型地震作用;隔震層位移的最大值之比約為2.49,平均值之比約為2.25;層間位移的最大值之比約為2.25,平均值之比約為2.17;樓層加速度的最大值之比約為1.71,平均值之比約為2.24。

(2) 近斷層地震作用下,層間位移呈反C形,1、2層較大,3～5層逐漸減小;樓層加速度沿高度呈C形分布或隨高度的增加而增大,其中近斷層脈沖型地震作用引起樓層加速度C形分布的概率明顯大于非脈沖型地震作用。

(3) 整體而言,近斷層脈沖型地震作用下的設備加速度和位移大于非脈沖型地震作用,設備加速度的最大值之比約為1.06,平均值之比約為1.17,設備位移的平均值之比約為1.20。這說明近斷層地震動中的脈沖特性對設備-結構耦合隔震體系中的設備響應有影響。

由上述對比可知,近斷層地震動的脈沖特性對結構的影響大于設備;近斷層脈沖型和非脈沖型地震作用下結構位移和加速度平均響應的比值>2.0,而設備位移和加速度平均響應的比值≤1.2。引起隔震層最大變形的地震動對應的設備響應并不一定最大,需結合樓面時程的頻譜特性進行具體分析。