雙向速度脈沖地震下偏心重力柱-核心筒結(jié)構(gòu)的彈塑性地震響應(yīng)研究

補國斌, 徐 沖, 賓 佳, 熊浩然, 齊超文, 王 穎

(湖南工業(yè)大學(xué) 土木工程學(xué)院, 湖南 株洲 412007)

0 引言

近年來,不規(guī)則建筑結(jié)構(gòu)體系得到了快速的發(fā)展,偏心建筑形式也成為建筑發(fā)展的趨勢之一。針對偏心結(jié)構(gòu)體系,專家和學(xué)者對其在抗震能力和應(yīng)用方面進行了廣泛的研究。Bu等[1]對框架結(jié)構(gòu)在強震和偏心雙重不利條件下進行了地震易損性分析;夏玲濤等[2]以結(jié)構(gòu)雙向偏心對結(jié)構(gòu)實用抗震設(shè)計與計算方法進行了深入研究;補國斌[3]以框架結(jié)構(gòu)為例,對其在偏心不利條件下展開了抗震性能和設(shè)計方法的研究。隨著經(jīng)濟的不斷發(fā)展,新型結(jié)構(gòu)體系成為城市發(fā)展的趨勢之一。創(chuàng)新提出并研究新型結(jié)構(gòu)體系的抗震性能,并完善相關(guān)的結(jié)構(gòu)設(shè)計理論,對促進我國高層建筑結(jié)構(gòu)的快速發(fā)展有舉足輕重的意義。周靖等[4-5]創(chuàng)新性地提出了一種適用于建筑工業(yè)化的新型重力柱-核心筒結(jié)構(gòu)體系,把傳統(tǒng)的節(jié)點連接方式由剛接改為鉸接,并完成了其在多種不同水準(zhǔn)地震作用工況下的振動臺試驗研究。張鴻森[6]對全鉸接混凝土核心筒結(jié)構(gòu)進行了抗震性能研究,并針對實際工程實例進行了縮尺振動臺模擬試驗。但專家和學(xué)者在對該新型結(jié)構(gòu)體系進行系統(tǒng)性抗震性能研究時尚未考慮結(jié)構(gòu)不規(guī)則因素。

歷次震害表明,近斷層速度脈沖地震作用對各類工程結(jié)構(gòu)的地震響應(yīng)產(chǎn)生顯著的影響,更容易導(dǎo)致建筑物發(fā)生倒塌或破壞[7]。因此,國內(nèi)外學(xué)者對該類地震及其對工程結(jié)構(gòu)的影響進行了一系列的研究,其研究結(jié)果表明,建筑結(jié)構(gòu)在脈沖型地震作用工況下的受力和變形等地震需求顯著高于非速度脈沖地震作用下的相應(yīng)需求值。總之,綜合考慮結(jié)構(gòu)平面和結(jié)構(gòu)豎向不規(guī)則效應(yīng)與脈沖地震動效應(yīng)對建筑結(jié)構(gòu)體系抗震性能耦合影響的研究工作較為缺乏,特別是針對考慮兩種不利條件下新型結(jié)構(gòu)體系的抗震性能研究工作更為少見[8-9]。

因此,本文以文獻[4]所述的新型重力柱-核心筒結(jié)構(gòu)體系及其在不同地震工況下的試驗數(shù)據(jù)為原始依據(jù),進行擴展參數(shù)化數(shù)值模擬與分析,研究新型結(jié)構(gòu)質(zhì)量偏心(平面不規(guī)則)和速度脈沖地震作用雙重不利條件共同作用下新型重力柱-核心筒結(jié)構(gòu)的非線性地震反應(yīng)規(guī)律,以期為近斷層區(qū)域新型重力柱-核心筒結(jié)構(gòu)體系的設(shè)計提供有益參考。

1 振動臺試驗及其模擬

1.1 重力柱-核心筒結(jié)構(gòu)體系簡介與試驗?zāi)Ｐ透艣r

新型重力柱-核心筒結(jié)構(gòu)體系[4]是基于傳統(tǒng)核心筒結(jié)構(gòu)基礎(chǔ),將外框架柱與內(nèi)部核心墻體的連梁以及外框架柱之間的連梁兩端連接方式變?yōu)槁菟ㄟB接,實際中考慮為鉸接(圖1)。這樣,核心筒的彎矩和剪力不傳遞到外框架。核心筒抵抗側(cè)移和抵抗扭矩的能力強,外框架則考慮只承受重力荷載。兩者分工明確,且不用糾結(jié)于傳統(tǒng)設(shè)計方式中框架最小剪力比要求,受力更合理,設(shè)計過程更加簡潔[9]。

圖1 螺栓鉸接節(jié)點Fig.1 Pinned connection of bolt

文獻[4]以廣西金融大廈的工程案例為原型,對總高度320 m的原型結(jié)構(gòu)進行了適當(dāng)?shù)暮喕?并建立1∶40縮尺試驗?zāi)Ｐ汀Ｔ囼災(zāi)Ｐ腿鐖D2(a)所示,高8.253 m，共37層。關(guān)于試驗詳情見參考文獻[4]。

1.2 原型結(jié)構(gòu)數(shù)值模擬與結(jié)果對比

采用CANNY[10]軟件對試驗?zāi)Ｐ蛯?yīng)的原型結(jié)構(gòu)進行彈塑性地震響應(yīng)分析。其有限元數(shù)值建模如圖2(b)所示。結(jié)構(gòu)各樓層混凝土標(biāo)號和鋼筋材料型號的具體介紹詳見文獻[10]。采用CANNY軟件中的內(nèi)置CS4模型(混凝土指數(shù)函數(shù)模型)和SR4模型(鋼筋四段式模型)分別模擬混凝土和鋼筋的本構(gòu)關(guān)系。其應(yīng)力-應(yīng)變行為如圖3所示,具體材料參數(shù)設(shè)置見文獻[10]。采用纖維模型模擬墻柱的壓(拉)彎耦合受力行為,采用內(nèi)置的CA7模型模擬構(gòu)件的抗剪,鋼梁采用桁架二力桿單元考慮軸向拉壓作用。所有參數(shù)的取值基于CANNY程序推薦的缺省值。

圖2 試驗?zāi)Ｐ秃蛿?shù)值模型Fig.2 Experimental model and CANNY numerical model

基于CANNY軟件構(gòu)建原型結(jié)構(gòu)的有限元數(shù)值模型并進行數(shù)值結(jié)果對比與分析驗證。對原型結(jié)構(gòu)在7度小震、中震和大震作用下進行彈性和彈塑性分析,得到其動力時程分析數(shù)值模擬結(jié)果。

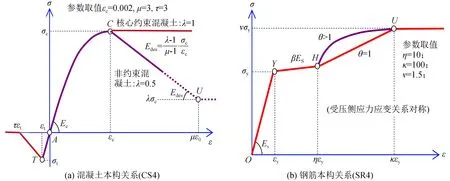
圖3 相關(guān)材料本構(gòu)關(guān)系Fig.3 Constitutive relationship of relative materials

采用CANNY程序得到的數(shù)值計算結(jié)果與通過相似比轉(zhuǎn)換得到的原型試驗數(shù)據(jù)的對比如圖4所示。由圖可知,數(shù)值計算和試驗結(jié)果基本接近,兩條曲線的吻合度較高。因此,可以采用相同的材料和模型參數(shù)設(shè)置,進行后續(xù)的擴展化數(shù)值模擬分析。

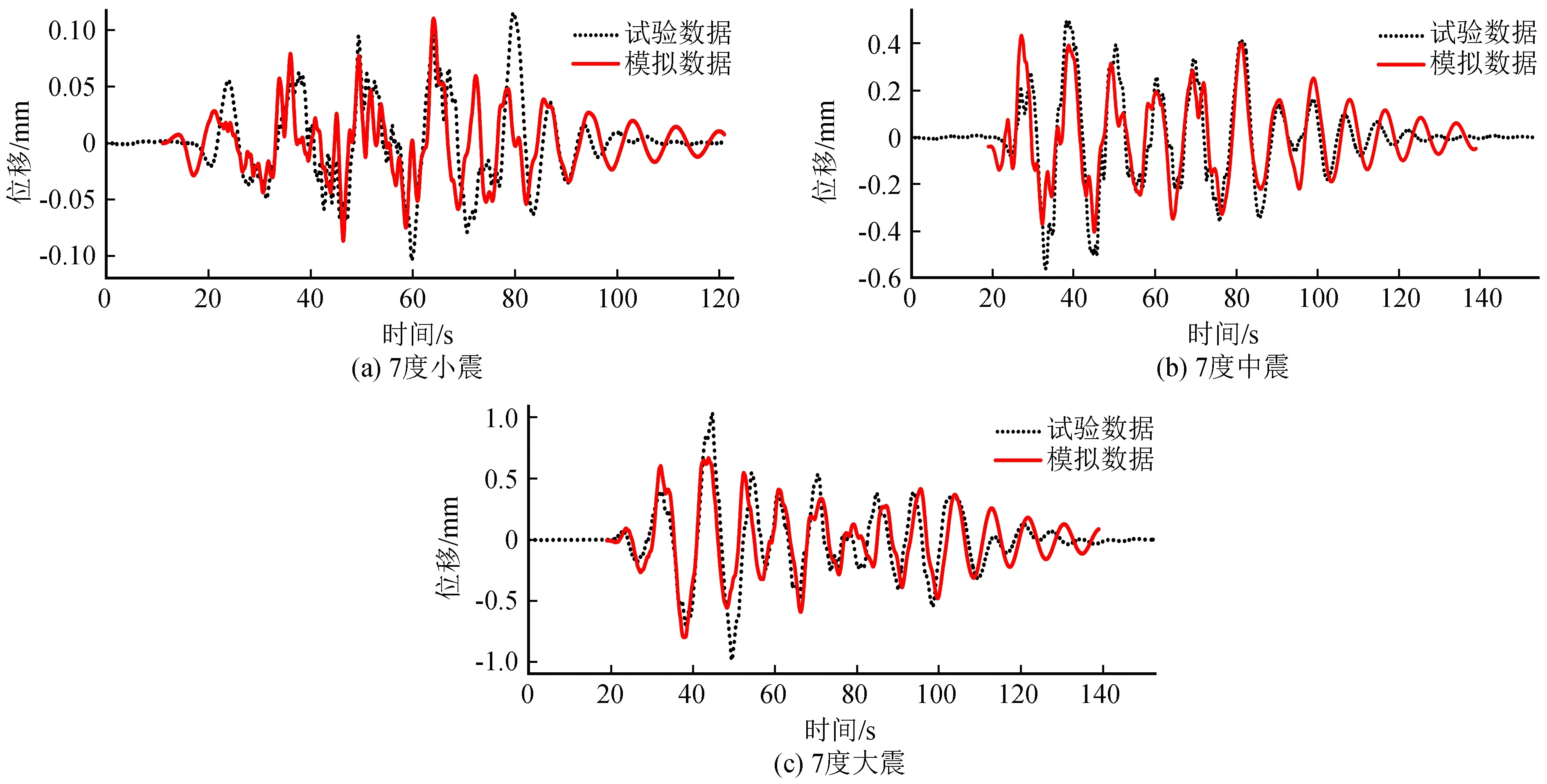
圖4 位移時程比較Fig.4 Comparison between displacement time history

2 結(jié)構(gòu)模型、地震動輸入與分析方法

2.1 偏心結(jié)構(gòu)模型

以1.1節(jié)振動臺試驗對應(yīng)的原型結(jié)構(gòu)為基礎(chǔ),采用YJK軟件[11]分別設(shè)計不同層高的典型新型結(jié)構(gòu)模型(20層和30層模型),如圖5所示。其結(jié)構(gòu)平面布置如圖6所示,結(jié)構(gòu)質(zhì)量偏心的實現(xiàn)方法為:以Y軸為對稱軸通過改變Y軸兩側(cè)的質(zhì)量(減小左邊,增大右邊,保持總質(zhì)量不變),從而實現(xiàn)結(jié)構(gòu)偏心。本文新型結(jié)構(gòu)涉及的質(zhì)量偏心僅考慮沿X軸方向。結(jié)構(gòu)質(zhì)量偏心率的計算公式為:

(1)

式中:em為建筑結(jié)構(gòu)物的質(zhì)量偏心距;L為結(jié)構(gòu)沿X方向的總長度;mi為第i個節(jié)點的集中質(zhì)量；xi為單個構(gòu)件(如第i個重力柱或第i片混凝土核心筒墻體)的質(zhì)量中心距幾何中心的距離。

圖5 YJK模型Fig.5 YJK model

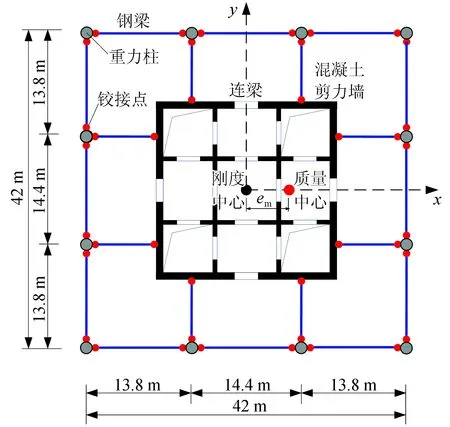
圖6 結(jié)構(gòu)平面布置圖Fig.6 Structural layout plan

相關(guān)研究表明,在各類偏心體系中,各個樓層均出現(xiàn)偏心的情況較為不利,但情況過多,無法窮舉,研究者往往選取各層均勻偏心工況。因此,本文亦選取結(jié)構(gòu)各樓層質(zhì)量均勻偏心體系進行非線性動力時程分析。利用CANNY有限元軟件進行數(shù)值模擬,材料選擇和結(jié)構(gòu)參數(shù)設(shè)置同1.1節(jié)。

2.2 地震動輸入與分析方法

震害調(diào)查表明,結(jié)構(gòu)在近場(近斷層或近源)速度脈沖型地震動作用下更容易發(fā)生破壞。考慮地震作用的隨機性和復(fù)雜性,基于太平洋地震工程研究中心(PEER)地震數(shù)據(jù)庫選取表1所列10條近場速脈沖型地震加速度記錄(原始加速度記錄),編號為O1～O10,以及其相對應(yīng)的非速度脈沖型地震地面加速度記錄用以進行對比分析,其編號為R1～R10,具體地面運動加速度數(shù)據(jù)見文獻[12]。速度脈沖地震特性采用Baker定義的PI值進行表征[12],0.85≤PI≤1為脈沖區(qū)間,0≤PI≤0.15為非脈沖區(qū)間。按建筑抗震設(shè)計規(guī)范5.1.2條,采用雙向地震動作為激勵進行輸入,輸入的比例為X∶Y=0.85。分析中考慮了4種偏心率,分別為0、0.1、0.2、0.3;2類地震類型(脈沖型與非脈沖型);20條地震加速度記錄;峰值地面加速度考慮0.5g以使結(jié)構(gòu)進入充分的彈塑性反應(yīng)階段。采用Newmark-Beta法數(shù)值分析方法,采用瑞雷阻尼,對應(yīng)第一、二階阻尼比,均設(shè)置為0.05。

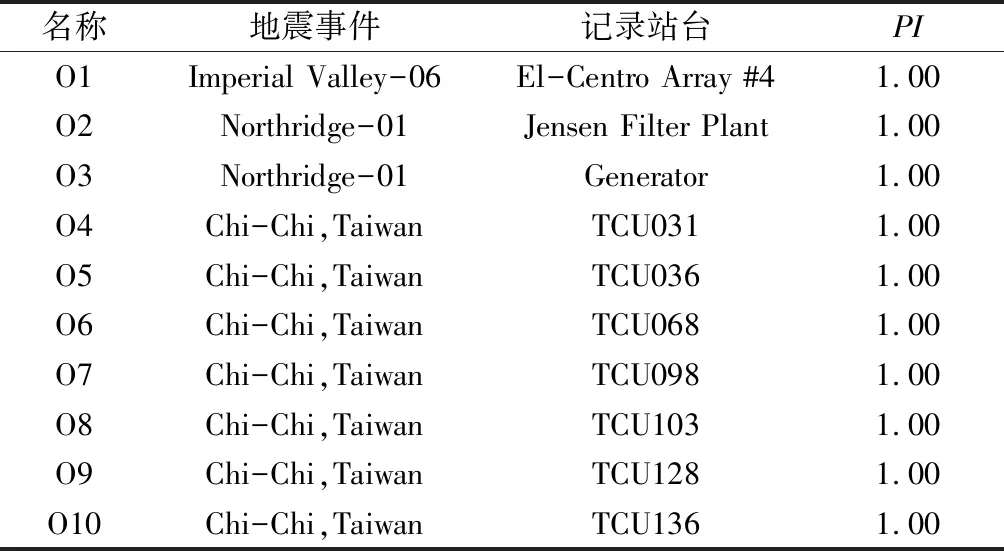
表1 10條速度脈沖型地震動記錄

3 數(shù)值分析結(jié)果與討論

分析結(jié)果表明,脈沖工況和非脈沖工況下,10條地震波下得到的結(jié)構(gòu)彈塑性響應(yīng)規(guī)律具有類似性。因此,3.1節(jié)以一條脈沖地震波為例進行層間位移角初步分析。3.2～3.4節(jié)則以10條地震波的彈塑性分析結(jié)果取其平均值對整體結(jié)構(gòu)進行分析。以下各圖中,速度脈沖和非速度脈沖地震波工況分別簡稱為脈沖和非脈沖工況。“e”表示結(jié)構(gòu)的質(zhì)量偏心率,例如,圖中“e0.2”表示質(zhì)量偏心率為0.2。

3.1 單條地震波下層間位移角響應(yīng)規(guī)律

圖7表示不同偏心率下20層結(jié)構(gòu)在表1中O8地震工況下各樓層的Y向和X向?qū)娱g位移角θmax的變化規(guī)律。由圖可知,兩個方向的θmax均隨著偏心率增大而增大(曲線呈現(xiàn)出外擴趨勢);偏心率一定時,θmax隨著樓層高度的增大呈現(xiàn)先增后減的趨勢。兩個方向的定性變化規(guī)律一致,但從θmax的響應(yīng)量值看Y方向明顯大于X方向?qū)?yīng)值。因此,后續(xù)的分析均取用更為不利的Y方向進行對比和分析。

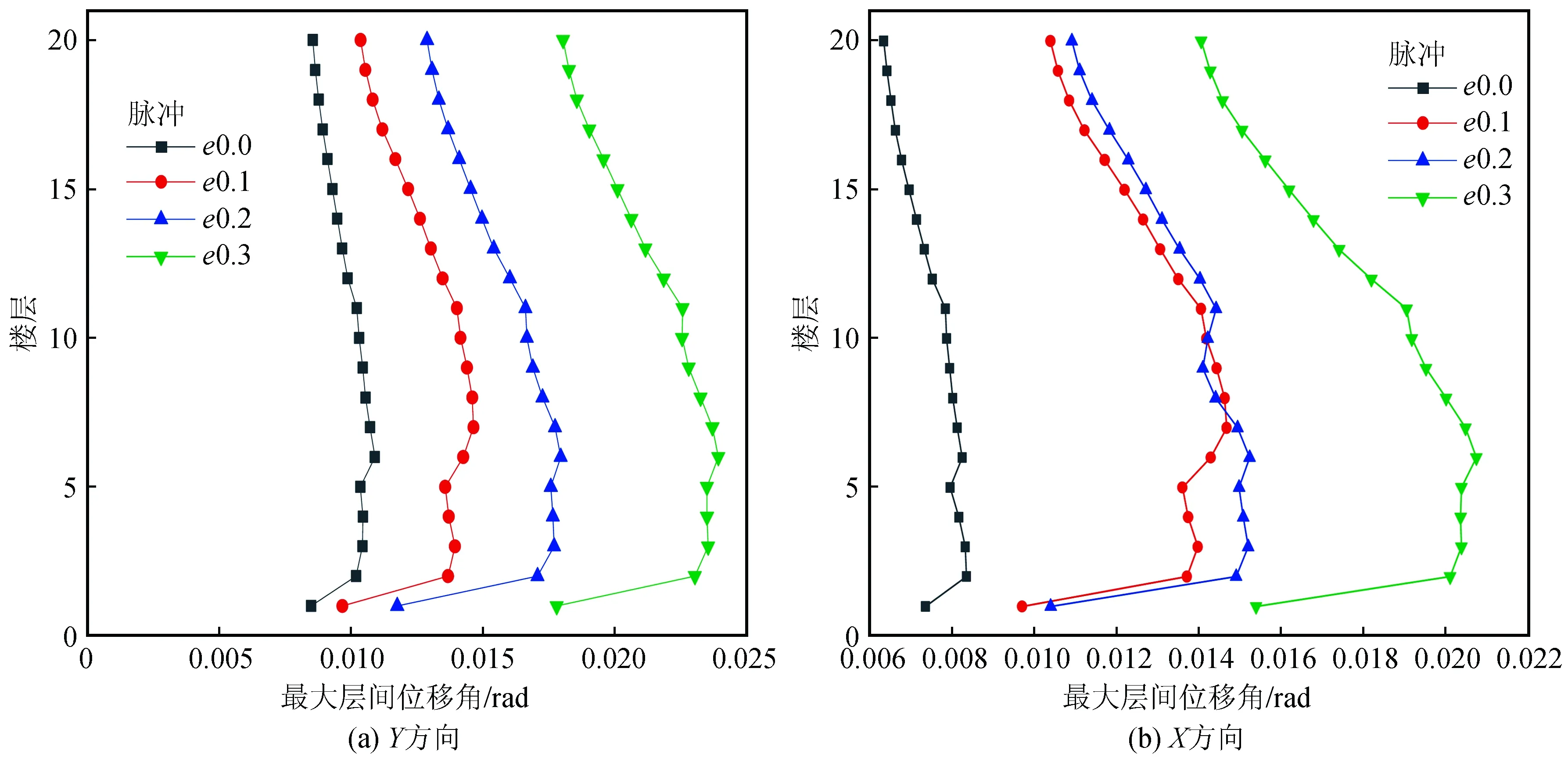
圖7 層間位移角Fig.7 Story drift ratio

3.2 質(zhì)量偏心和速度脈沖對層間位移角的影響

圖8(a)、(b)分別表示在速度脈沖型和非速度脈沖型地震動作用下,20層和30層結(jié)構(gòu)的最大層間位移角(θmax)隨結(jié)構(gòu)偏心率的變化規(guī)律。由圖可知,兩種工況下20層和30層結(jié)構(gòu)的θ均隨著偏心率增大而增大,且速度脈沖工況(實線)下的θmax明顯大于非速度脈沖工況(虛線)。為了更深入地探討結(jié)構(gòu)整體θmax的響應(yīng)規(guī)律,取圖8(a)和(b)各條曲線的最大值進行定量分析,如圖8(c)表示不同偏心率下20層和30層結(jié)構(gòu)θmax的響應(yīng)規(guī)律。脈沖和非脈沖工況下,θmax均隨偏心率增大而增大。脈沖工況下,偏心率為0.3時20層和30層結(jié)構(gòu)的θmax分別增大到無偏心結(jié)構(gòu)對應(yīng)值的2倍和1.4倍。同時,速度脈沖工況下的θmax明顯大于非速度脈沖工況。當(dāng)偏心率為0.3時,20層和30層結(jié)構(gòu)在脈沖工況下的θmax達到非脈沖工況的1.7倍和1.6倍。這表明結(jié)構(gòu)偏心和速度脈沖地震效應(yīng)均會顯著增大結(jié)構(gòu)的位移響應(yīng),在新型體系的抗震設(shè)計中應(yīng)引起足夠重視。

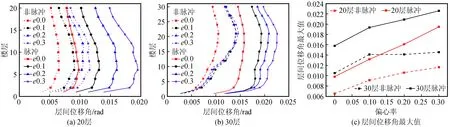
圖8 層間位移角變化規(guī)律Fig.8 Change law of the story drift ratio

3.3 質(zhì)量偏心和速度脈沖對層間扭轉(zhuǎn)角的影響

圖9(a)、(b)表示20層和30層結(jié)構(gòu)在速度脈沖和非速度脈沖工況下層間扭轉(zhuǎn)角(φmax)隨偏心率的變化規(guī)律。由圖可知,兩種工況下20層和30層結(jié)構(gòu)的φmax均隨著偏心率增大而增大,且脈沖工況(實線)下的φmax均大于非脈沖工況(虛線)。為了更深入地探討結(jié)構(gòu)整體φmax的響應(yīng)規(guī)律,取圖9(a)和(b)各條曲線的最大值進行定量分析。圖9(c)表示20層和30層結(jié)構(gòu)隨偏心率的變化結(jié)構(gòu)φmax的響應(yīng)規(guī)律。在速度脈沖和非速度脈沖兩種不同工況下,φmax均隨著偏心率增大而增大。速度脈沖工況下,偏心率為0.3時20層和30層結(jié)構(gòu)的φmax分別增大到無偏心結(jié)構(gòu)對應(yīng)值的20.6倍和16.9倍。同時,速度脈沖工況下的φmax明顯大于非速度脈沖工況。當(dāng)偏心率為0.3時,20層和30層結(jié)構(gòu)在脈沖工況下的φmax達到非脈沖工況的1.5倍和1.3倍。這表明結(jié)構(gòu)偏心和速度脈沖地震效應(yīng)均會顯著增大結(jié)構(gòu)的扭轉(zhuǎn)效應(yīng),在新型體系的抗震設(shè)計中應(yīng)予以重視。

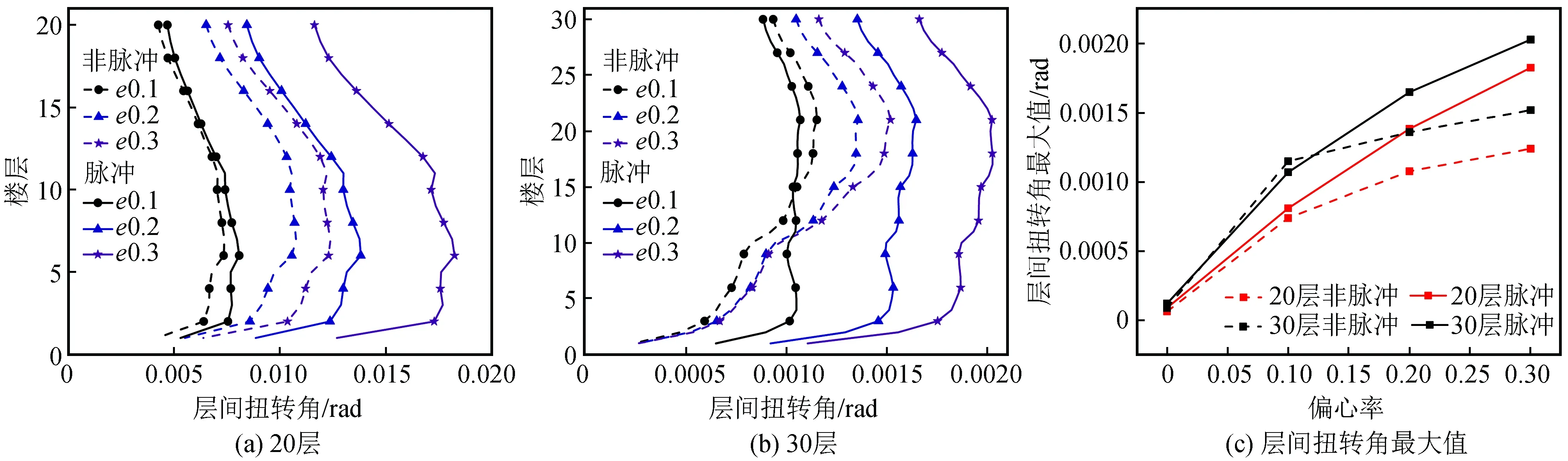
圖9 層間扭轉(zhuǎn)角變化規(guī)律Fig.9 Change law of the inter-story torsion angle

3.4 質(zhì)量偏心和速度脈沖對層間剪力的影響

圖10(a)、(b)表示20層和30結(jié)構(gòu)在速度脈沖和非速度脈沖工況下,不同偏心率對結(jié)構(gòu)層間剪力(Vmax)的響應(yīng)規(guī)律。由圖10可知,在兩種地震工況下,20層和30層兩種樓層結(jié)構(gòu)的Vmax均隨著偏心率增大而減小,且脈沖工況下的Vmax均大于非脈沖工況。包絡(luò)線均有內(nèi)收趨勢,此規(guī)律與文獻[13]類似,原因可能是地震動雙向輸入,當(dāng)偏心率不斷增大,結(jié)構(gòu)的扭轉(zhuǎn)效應(yīng)也隨之增大,與地震動輸入主方向垂直的另一方向分擔(dān)了部分剪力,導(dǎo)致主向的Vmax減小。

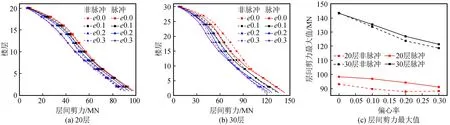
圖10 層間剪力變化規(guī)律Fig.10 Change law of the inter-story shear force

為了更加深入地探討結(jié)構(gòu)整體最大層間剪力Vmax的響應(yīng)規(guī)律,取圖10(a)和(b)各條曲線的最大值進行定量分析。圖10(c)表示20層和30層兩種樓層結(jié)構(gòu)在速度脈沖和非速度脈沖兩種工況下結(jié)構(gòu)Vmax在不同偏心率下的響應(yīng)規(guī)律。脈沖和非脈沖工況下,Vmax均隨偏心率增大而減小。脈沖工況下,偏心率為0.3時20層和30層結(jié)構(gòu)的Vmax分別約減小到無偏心結(jié)構(gòu)對應(yīng)值的90%和80%。同時,脈沖工況下的Vmax略大于非脈沖工況。當(dāng)偏心率為0.3時,20層和30層結(jié)構(gòu)在脈沖工況下的Vmax比非脈沖工況對應(yīng)值約大3%和2%。

4 結(jié)語

本文基于振動臺試驗研究基礎(chǔ),通過對20層和30層新型偏心結(jié)構(gòu)體系在速度脈沖和非速度脈沖地震作用下的對比分析,重點研究結(jié)構(gòu)偏心與脈沖地震耦合效應(yīng)對結(jié)構(gòu)的層間位移角、層間扭轉(zhuǎn)角和層間剪力的影響規(guī)律,得到以下結(jié)論。

(1) 新型重力柱-核心筒結(jié)構(gòu)在速度脈沖和非速度脈沖兩種工況下,隨著偏心率的不斷增大結(jié)構(gòu)θmax和φmax也隨之增大,且速度脈沖工況下的θmax和φmax均顯著大于非速度脈沖工況下的對應(yīng)值。當(dāng)偏心率為0.3時,在速度脈沖工況下20層和30層兩種樓層結(jié)構(gòu)的θmax分別為非速度脈沖工況下的1.7倍和1.6倍;最大層間扭轉(zhuǎn)角的相應(yīng)倍數(shù)為1.5和1.4倍。

(2) 新型偏心結(jié)構(gòu)體系的層間剪力隨著偏心率的增大呈現(xiàn)出減小的趨勢。同時,速度脈沖地震效應(yīng)對偏心結(jié)構(gòu)體系層間剪力有一定影響。當(dāng)偏心率為0.1時,在速度脈沖工況下20層和30層兩種樓層結(jié)構(gòu)的Vmax的最大值比非速度脈沖工況下的對應(yīng)值分別約大3%和2%。建議在新型重力柱-核心筒結(jié)構(gòu)體系的抗震研究中,針對速度脈沖型地震和質(zhì)量偏心對結(jié)構(gòu)產(chǎn)生的位移和扭轉(zhuǎn)變形放大效應(yīng)予以重點關(guān)注。