“實數”單元作業的設計、反饋與優化*
浙江省杭州市余杭區閑林中學 楊淑萍 程龍軍
數學單元作業的主要功能在于鞏固知識、診斷教學、學科育人.審視當下的單元作業,往往是只呼應一些低層次機械訓練的作業目標,過度關注知識和技能的鞏固,缺少對應于高階思維和應用性的作業設計.這就需要我們在關注課程目標的同時,發揮數學作業的應有功能,適當增加創新性作業設計,助力課程目標的整體實現.為此,本文中以浙教版七年級上冊“實數”單元作業設計為例進行說明.
1 作業目標
本章共分四個小節,主要內容包括數的開方、平方根、立方根、實數及其運算.其中,平方根與立方根屬于核心概念.從操作意義上看,根號作為一個過程可以代表運算符號;從結構意義上看,它作為一個對象又可以代表運算的結果.與加減乘除運算相比,其概念抽象難懂,在處理具體問題時易混淆根號的過程性和結構性.基于此,在參考《義務教育數學課程標準》的基礎上,作業目標可以適當增加抽象概念理解的相關內容.具體作業目標如下:
(1)加深對平方根、算術平方根、立方根、無理數、實數等概念的理解,知道開平方與平方、開立方與立方互為逆運算,實數與數軸上點的一一對應關系;
(2)會準確表示和計算一個數的平方根和立方根,能進行簡單的實數四則運算,會估算一個無理數的范圍,會求實數的相反數與絕對值;
(3)通過解決實際問題發展數感和符號意識,體會數形結合和分類討論思想.
2 設計思路
為適應不同學生的學力水平,滿足個性化的需求,作業設置分為回顧、強化、提升和應用四個層次.回顧環節幫助學生梳理知識點,形成知識結構;強化環節針對開平方和開立方運算進行專項訓練,為后續學習二次根式的內容奠定基礎;提升環節則綜合多個知識點,考查學生分析和解決問題的能力;應用環節結合生活中的實際問題,使學生感受學習相關知識的必要性和應用價值,發展學生的應用意識和創造性思維.
3 初次設計及反饋
3.1 回顧
(1)下列說法錯誤的是( ).
A.無理數就是無限不循環小數
B.算術平方根等于本身的數是0和1
C.正數,0,負數都有立方根
D.因為3的平方是9,所以9的平方根是3
(2)填寫表1:(不能開方的數寫“無”,開不盡方的數保留根號.)
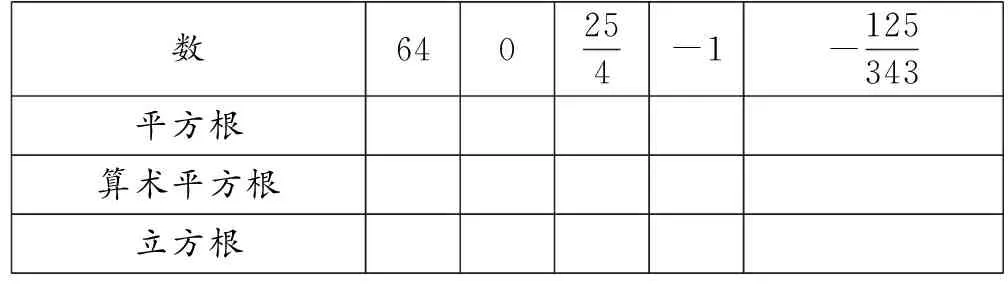
表1
(3)把下列各數填在相應的橫線上:

有理數:
.
無理數:
.
(4)將下列各數近似地表示在數軸上,并用“<”表示.
設計意圖:第(1)(2)兩題引導學生回顧平方根、算術平方根、立方根的概念以及性質,題中既包括了正數、負數和0,也包括了分數,目的是使學生對概念有全面的理解,同時也考查簡單的開方計算.第(3)題考查了實數的概念與分類,重點讓學生認清與π相關的數、開方開不盡的數、有規律但不循環的數這三類無理數.第(4)題考查了實數的大小比較和開立方運算,了解實數與數軸上點的一一對應關系,感受數形結合思想.
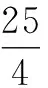
3.2 強化
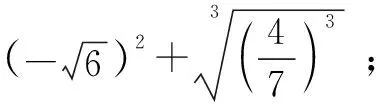
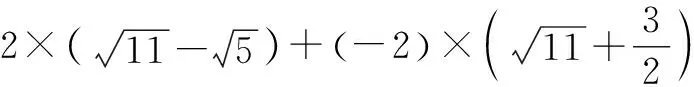
設計意圖:開方運算可為后續學習二次根式奠定重要基礎.第①②小題強化考查平方根、算術平方根、立方根的計算;第③小題則考查學生對開方運算與乘方運算互逆關系的深刻理解;第④小題是較復雜的混合運算,需要運用乘法分配律以及計算器求無理數的近似值.
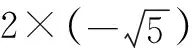
3.3 提升

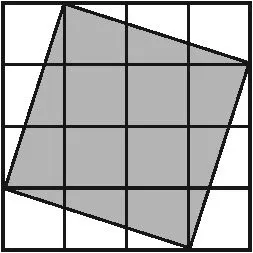
圖1
(7)如圖1,每個小方格的邊長為1個單位長度,則陰影正方形的面積是,邊長是.
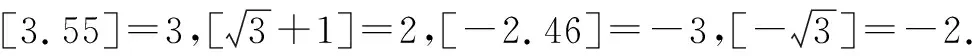
設計意圖:第(6)題難度增大,綜合了絕對值和算術平方根的概念、實數的加減運算以及分類討論等多個知識點.第(7)題結合實際問題考查了面積法和開平方運算,強化了符號語言、文字語言和圖形語言的相互轉化,引領學生借助數形結合,直觀感受無理數的大小和客觀存在,克服理解數在擴展過程中的抽象性困難.第(8)題是新定義問題,涉及的知識點是夾逼法估算無理數和負數的大小比較.
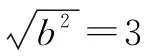
3.4 應用
(9)小實同學手中有一塊長方形紙板和一塊正方形紙板,其中長方形紙板的長為3 dm,寬為2 dm,且兩塊紙板的面積相等.
①求正方形紙板的邊長(結果保留根號);
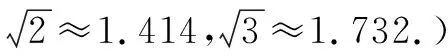
(10)小實手上有三張卡片,分別印有1,-125,196,請你從中抽出兩張卡片,并以卡片中的數設計一個算式,要求算式中至少包括開方運算,且滿足下列要求.
①結果為有理數:
.
②結果為無理數:
.
設計意圖:本環節的兩個問題基于開放性、探究性和趣味性的原則進行設計.第(9)題需要運用無理數處理實際問題,考查學生動手畫圖能力和對無理數的估算能力,培養數感和以形助數的意識.第(10)題兼具開放題和趣味性,借助“抽卡片”游戲考查學生對開方運算的理解.

4 思考及優化
4.1 初次作業設計的思考
本次作業經課后統計,50%的學生在25分鐘內完成,82%的學生在30分鐘內完成.從反饋分析來看,此次作業量雖然符合作業要求,但部分試題難易不均、功能重疊,編排順序也不夠合理,因此進行如下思考與改進.
首先,回顧知識,厘清結構.設計作業時,需要注重單元知識間的相互聯系,對教學內容進行結構化處理,幫助學生形成良好的認知結構.只有從單元整體上考慮作業設計、分析及評價,強調關聯性,才能真正體現“整體架構”.縱觀上述設計,缺少了一個梳理知識的結構化問題.
其次,基本概念,學深悟透.平方根和立方根的概念既是重點也是難點,從反饋的問題來看,學生對根號的認識不夠清晰,不理解根號既表示開方運算也表示運算結果,以及在何種情況下表示運算而又在何種情況下表示結果.因此,對原第(1)題進行替換以加強學生對根號的理解.
再次,分層設計,優化細節.分層設計和循序漸進是作業設計的重要原則.第(6)題的知識點綜合性強且錯誤率高,故將其與第(7)題調整順序;第(10)題與第(9)題功能重疊,且思維含量不高,予以刪除.
最后,降低難度,突出重點.強化訓練是掌握數學知識的有效方法,但需要做到少而精,一味脫離對概念的理解而單純搞題海戰術,容易催生學生對作業倦怠,影響學生的學習興趣.第(5)題中的③④小題運算難度較大,故進行替換以鞏固實數運算的順序和符號問題;第(8)題需要區分負數的整數部分和小數部分,還涉及負數的大小比較,對學生的理解和綜合能力要求較高,也超出了課標要求,予以刪除.
4.2初次作業設計的優化
4.2.1 回顧
(1)如圖2,完善以下知識結構圖:
(2)下列選項正確的是( ).

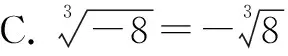
(3)填表(如前表1):(不能開方的數寫“無”,開不盡方的數保留根號.)
(4)把下列各數填在相應的橫線上:

有理數:
.
無理數:
.
(5)將下列各數近似地表示在數軸上,并用“<”表示.
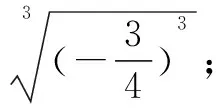
4.2.2提升
(7)如圖1,每個小方格的邊長為1個單位長度,則陰影正方形的面積是,邊長是.

4.2.3 應用
(9)小實同學手中有一塊長方形紙板和一塊正方形紙板,其中長方形紙板的長為3 dm,寬為2 dm,且兩塊紙板的面積相等.
①求正方形紙板的邊長(結果保留根號);
5 幾點建議
(1)問題設計的指向性
為了保證教學評的一致性,問題的設計需要與作業目標一致,教師需要細致分析相關知識點再進行精準設計,確立好作業內容后,依據目標逐條分析二者的對應情況,也可以做一些數據的分析和統計,進而對作業設計的內容乃至作業目標本身進行適當的調整.問題的設計還需要與課程標準倡導的“四基”相聯系,既要指向基礎知識和基本技能,也要指向基本思想方法和基本活動經驗.此外,還要重視作業與課堂教學內容的緊密結合,既要面面俱到,又要杜絕知識點的簡單重復,力求指向學習重點,充分發揮作業鞏固知識和診斷的教學功能.
(2)問題序列的層次性
作業設計需要考慮不同學生的個性化學習需求,既要鞏固基礎,讓學生感受學習的樂趣,也要提升和應用,讓學生對知識有更深層次的思考.本單元作業設計了回顧、強化、提升和應用四個層次,難度由淺入深,尊重了學生的個體差異.回顧部分指向基礎知識和基本技能,要求所有學生都要掌握,這也是課程標準的基本要求;提升部分強調知識的綜合運用,要求中等生和學優生會做;應用部分對學生的理解和應用能力要求較高,學生可根據自身實際能力選做.
(3)問題設計的創新性
王月芬博士指出,作業類型的多樣化有助于提髙學生的作業興趣,減輕作業壓力,同時對提高學生學業成績也存在較明顯的相關性.因此,數學作業類型和作業功能需要創新,由傳統的只重視雙基訓練向重視綜合能力的培養轉變,充分發揮數學開放題、變式題、探究題以及綜合實踐題的育人功能.通過開放題培養學生思維的發散性,拓展思維空間;通過變式題引導學生遷移運用,完善知識體系;通過探究題培養學生思維的深刻性,感受數學之美;通過實踐題體會數學與生活的密切聯系和多樣的學習方式,培養學生積極思考和主動探索的精神.

