平面幾何解題思路探析*

合肥師范學院數學與統(tǒng)計學院 唐亞軍 唐永生 賀小雪 李亞文

1 問題提出

初中平面幾何內容具有很強的實用性和基礎性，它不但在現代生活和生產中的應用非常廣泛，而且是進一步學習數學和其他學科必不可少的基礎[1].其中，平面幾何解題在培養(yǎng)學生的邏輯思維能力和科學的思維方法上起著非常重要的作用.但是學生在解答平面幾何問題時，常停留在記憶與模仿的階段，導致解題思維混亂，不知道從哪里入手以及需要遵循哪些規(guī)則等[2].因此，探析平面幾何解題的最優(yōu)化思路仍是數學教學研究的重要問題.

2 平面幾何解題思路

波利亞指出，問題解決的模式是一個不斷發(fā)展的過程，數學解題要探求解題模式的一般性.就平面幾何而言，幾何解題要嚴格遵守解題的各項規(guī)則，注重問題的識別與理解，注重制定與執(zhí)行解決問題的條件和對結果的檢驗[3].教會學生解題的思路，有利于形成學生的解題心理定式，這樣學生在不同的情境中都能快速地反應并解決問題.平面幾何問題的解題思路如圖1所示.

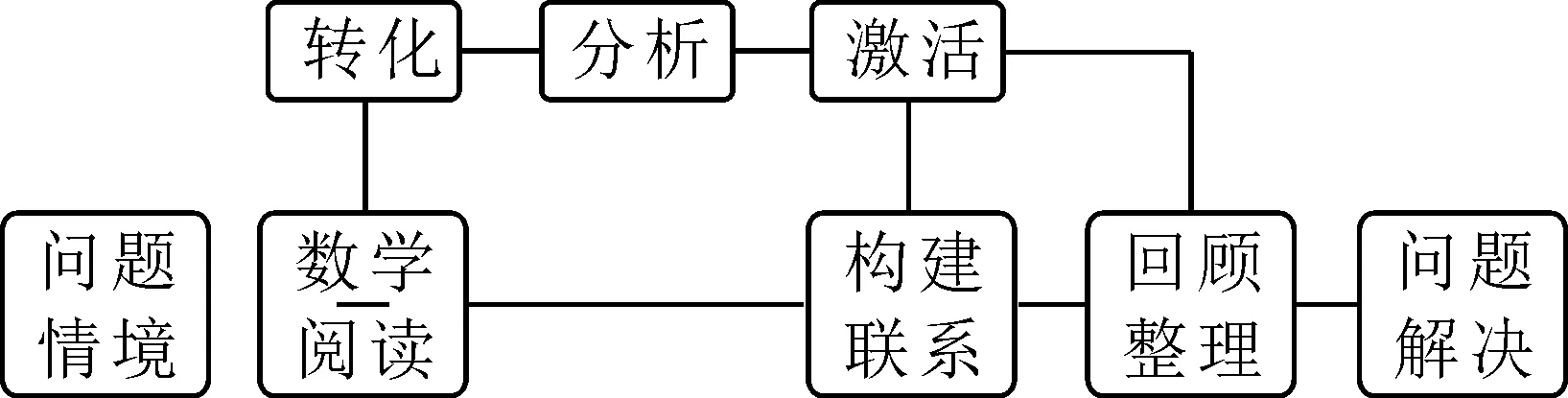
圖1

2.1 問題情境

格式塔心理學派問題解決觀認為，問題解決是對問題情境的整體理解.問題情境是個體所面臨的數學問題以及由問題所引起的舊的知識結構的再現.學生在面臨問題情境時，回想是否遇到過相似情境及其解決方法，或是以前的方法是否可以遷移.對問題的理解不同，學生思考問題的方向與思維習慣就會不同，進而所采用的方法也會不同.

2.2 數學閱讀

閱讀的目的是理解閱讀材料，提取其中有意義的信息.平面幾何解題中，數學閱讀則是摒棄幾何問題中的無關要素，對題設和圖形進行分析，提取出解決問題的關鍵性信息.數學閱讀是問題解決的起始環(huán)節(jié)和基礎步驟.題設閱讀是清楚所給的已知條件與結果，對題設所給的文字、符號等在腦海中進行預設與理解；幾何圖形閱讀就是學生根據所學知識對所給圖形進行識別.學生要善于將復雜的幾何圖形分解為有必然聯(lián)系的簡單基礎幾何圖形去把握圖形的本質[4]，進而為后面的解題提供基礎.(如圖2所示)

圖2

2.3 轉化、分析、激活

轉化，是指將題目中所給的數學語言(文字語言、符號語言、圖形語言)進行轉化，從而達到對問題的正確表征，把握問題的本質.分析，是指對已知條件與結果以及它們之間的關系進行分析.對已知條件的分析，即采用綜合法，逼近結果，由條件可以順推若干個幾何關系T1，T2，……，Tn；結果分析，即采用分析法，逼近條件，由結果溯流而上可以逆推若干個幾何關系Q1，Q2，……，Qn.推出條件T和Q的過程就是激活認知結構中條件與結果相關知識的過程.激活是一個搜尋與提取信息的過程，這個過程需要學生擁有非常豐富的知識結構.

2.4 構造聯(lián)系

構造聯(lián)系，是在分析條件與結果、激活相關知識的基礎上，建立已知與未知之間的聯(lián)系.比較T1，T2，……，Tn和Q1，Q2，……，Qn，如果其中的Ti和Qi之間存在明顯的關系或者Ti=Qi的話，通過綜合與分析，便可以構造未知與已知之間的聯(lián)系[5]，這樣問題便得到了解決；若比較T1，T2，……，Tn和Q1，Q2，……，Qn，通過已有的條件很難將兩者聯(lián)系起來，條件與結論之間存在著中間的未知條件M1，M2，……,Mn，其中有條件Mi存在于Ti和Qi之間，溝通了Ti和Qi或者Ti=Mi=Qi，從而順利地從條件到結果.未知條件M往往是通過巧妙地添加輔助線而得到，因此，一條好的輔助線往往能使復雜的問題變得簡單，輔助線的建立是解題的關鍵一步.(如圖3所示)

圖3

2.5 回顧整理

回顧,即重新思考分析問題的認知過程，是一種對自我認知的檢查.分析問題的時候難免會出現思維與邏輯上的錯誤，即使是正確的分析過程和解題思路，也要在回顧的過程中進行調整、修改、補充等，尋求解答過程的最優(yōu)化.整理，即整理分析過程，在這過程中，要注意數學語言的正確使用，盡量多使用數學符號語言，力求過程的精簡化；過程要符合語義和法則，注意正確把握各步驟間的邏輯推導關系.

3 平面幾何解題思路的應用

安徽省合肥市2021年壓軸題第21題是一道幾何題，非常典型，尤其是第(3)小問非常考驗學生的解題思維.

例如圖4-1，在四邊形ABCD中，∠ABC=∠BCD，點E在邊BC上，且AE∥CD，DE∥AB，作CF∥AD交線段AE于點F，連接BF.

(1)求證： △ABF≌△EAD；

(2)如圖4-2中，若AB=9，CD=5，∠BCF=∠AED，求BE的長；

圖4-1

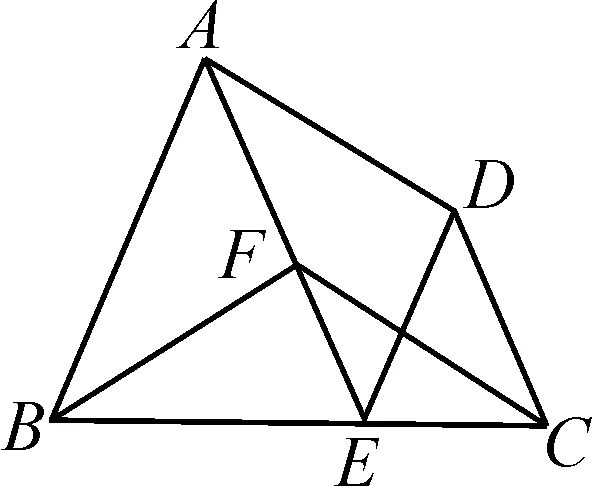
圖4-2

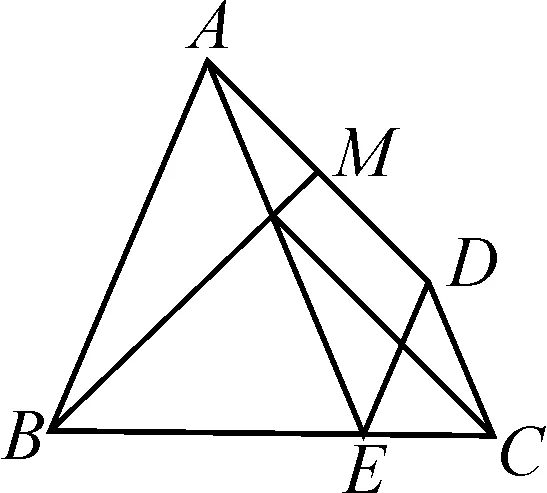
圖4-3

問題情境：這種多個問答的問題往往前一問的方法或者結論可以為下一問做參考.

數學閱讀：題干中給了7個條件，即四邊形ABCD,∠ABC=∠BCD,點E在邊BC上,AE∥CD，DE∥AB，CF∥AD，CF與AE交于點F；所給圖形中，以三角形為主，這個復雜的圖形可以看成：△ABE和△DEC頂點相連，也可以看成△ABE與梯形AECD拼成.問題(1)是證明全等；(2)是給定值，然后求BE的長；(3)中給定BF的延長線過AD的中點M,求比值.

轉化:將上述需要轉化的條件進行如下語言的轉化，

分析與激活：對已知條件進行如下分析.

①AE∥CD?∠AEB=∠DCE，∠AED=∠CDE，∠DCF=∠CFE；②DE//AB?∠ABE=∠DEC，∠BAE=∠AED；③∠ABC=∠BCD?∠ABE=∠AEB= ∠DEC=∠DCE?△ABE與△DEC為等腰三角形?AB=AE，DE=DC；④由①和②條件?∠BAE=∠AED=∠CDE；⑤CF//AD?∠DAF=∠CFE?∠DAF=∠CFE=∠DCF；⑥由③⑤?AFCD是平行四邊形?AF=CD?AF=CD=DE.

對第(1)問進行分析：(1)要求證△ABF≌△EAD?只需滿足SSS，SAS，ASA，AAS中的一個?邊角等量關系.

解析：(1)由上面分析可知，在△ABF和△EAD中AB=AE，∠BAE=∠AED，AF=DE，所以 △ABF≌△EAD(SAS).

由△ABF≌△EAD，可得AD=BF=CF，∠DAF=∠ABF=∠CFE=∠DCF.

解析：(2)由上述分析可知△ABE∽△BFE，則

因為AE=9，EF=4，所以BE2=36，即BE=6.

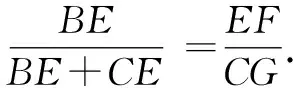
4 平面幾何解題思路的思考

任何解題的教學都是在學生已有的知識基礎之上的再發(fā)現、再建構的過程，在這個過程中學生對自己的思維進行監(jiān)控與調整.

4.1 學生的認知結構是解題思路的基礎

學生的已有知識總量和知識貯備方式等主觀因素是問題解決的根本因素.認知結構是學生由知識結構內化而形成的，是學生將學得的知識按照自己的理解組織起來的心理系統(tǒng)，它既是知識的建構方式，也是知識的貯備方式.學生頭腦中知識的良好結構和聯(lián)系與問題解決之間存在著明顯的相關性[6]，可以快速進行知識提取，全面激活關于條件與結論的相關知識點，更好地促進問題解決.任何解題思路都離不開學生原有的知識與經驗，這是學生學習的基礎.

4.2 解題思維過程的整體推進

解題步驟不是前后相繼的關系，而是在某個環(huán)節(jié)的基礎上同時進行的.學生在閱讀的同時，也進行著轉化的操作，邊閱讀,邊理解,邊轉化，這樣才能更加透徹地把握題目的全部內容.當轉化到一定的條件時，也就開始了分析與激活.因此，這幾個環(huán)節(jié)是環(huán)環(huán)相扣、不可分離的關系.后面步驟是在前面步驟的基礎上展開的，但此時并不意味著前面步驟的結束.

4.3 根據問題難易程度做出相應調整

雖然研究幾何解題思路是為了學生更好地解決問題，但是一味按照思路來解題勢必限制學生的思維，形成思維定式.因此，在幾何解題的過程中，應該根據問題的難易程度做出相應的調整、刪減等.對于稍微簡單一點的問題，在轉化的過程中就可以將問題解決；對于比較難的數學證明，則需要在分析的基礎上多次閱讀與轉化.

5 結論

平面幾何解題的過程中,學生的心理與思維起到關鍵的作用.學生提取自己的認知結構，對自己解題過程進行監(jiān)控，從而使問題得以解決.因此在教學中教師應該注重培養(yǎng)學生數學閱讀能力，完善學生認知結構，提高學生自我元認知，以此培養(yǎng)學生的幾何思維，提高學生的平面幾何的解題能力.