指向初中數學本質的幾何教學探究
——以浙教版八下“5.2.1菱形”為例

浙江省衢州市第四實驗學校 項志成 鄧 達

隨著課改的深入，課堂教學的方法、手段變得越來越豐富.既要提升學習興趣，又要提升學科素養，無不考驗著教師的教學智慧[1].章建躍博士指出：“數學課改的核心任務是提升學生的數學學科核心素養，要有具體措施，要把數學學科核心素養落實在數學教育的各個環節.”不管我們的教學形式如何變化，都應該堅持一個原則，即注重數學本質的呈現，這是數學教學的立足之本[2].筆者以浙教版八下“5.2.1菱形”為例，結合自身多年的實踐探究，提出個人的一些思考.

1 教學目標

(1)通過折紙活動，經歷菱形的概念生成和理解的過程.

(2)類比平行四邊形的研究方法和內容，經歷菱形性質的發現和推理驗證的過程.

(3)掌握菱形的性質定理“菱形的四條邊都相等”“菱形的對角線互相垂直，每條對角線平分一組對角”，并應用性質定理解決相關的數學問題.

2 教學設計

2.1 折——由“數學實驗”到“數學味道”

師生活動：取一張長方形紙片，按下圖1-1,1-2所示的方法對折兩次，并沿圖1-3中的斜線(虛線)剪開，把剪下的Ⅰ這部分展開，平鋪在桌面上.

師：剪出的這個圖形是平行四邊形嗎？你是如何判定的？

生1：是平行四邊形.由折疊可得兩對內錯角相等，因此兩組對邊分別平行.

生2：由折疊可以得到它的一組對邊平行且相等，或兩組對邊分別相等，或對角線互相平分.

師：這個平行四邊形還有什么特別之處？

生：它的四條邊都相等.

師：像這樣的平行四邊形，我們把它叫做菱形.類比矩形的定義，你能給菱形下定義嗎？

生：有一組鄰邊相等的平行四邊形叫做菱形.

設計意圖：折紙是教材中“菱形”第2課時合作學習中的內容，通過合理改編教材，利用數學實驗一方面幫助學生回顧平行四邊形的相關知識，另一方面讓學生經歷菱形的概念生成和理解的過程.通過設置問題串，引導學生發現圖形中要素之間的內在聯系，由“數學實驗”轉向“數學味道”，激發學生的探索欲望.

2.2 證——由“幾何直觀”到“邏輯推理”

在數學教學活動中，注重邏輯推理的培養，有利于學生理解一般結論的來龍去脈，形成舉一反三的能力，有利于學生提高探究事物本源的能力.

師：由定義可知，菱形是特殊的平行四邊形，因此它具有平行四邊形的所有性質.它還具有哪些特殊性質呢？

生：菱形的四條邊都相等，對角線互相垂直.

師：你是怎么發現的？

生3：通過觀察就能得到.

生4：我覺得可以通過折疊得到.(該生將手中菱形進行折疊.)

師：很好.但觀察、實驗并不等于證明，你能證明嗎？

生：可以.第一個性質利用平行四邊形的性質與菱形的定義即可證明.(該生講授證明過程后，教師板書該性質定理.)

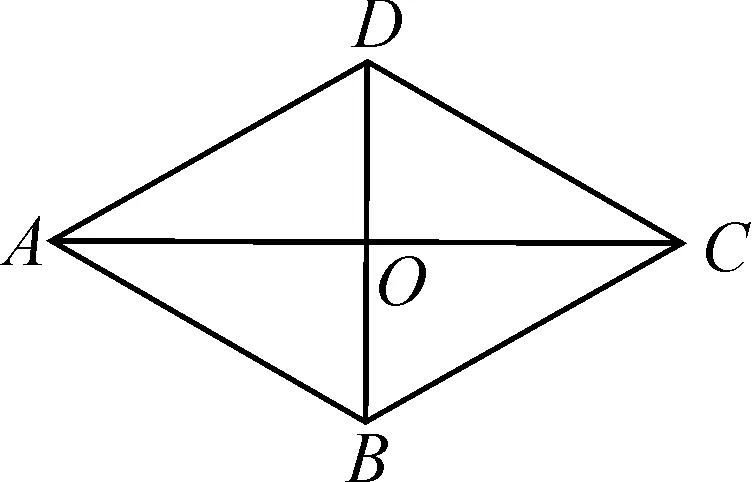
圖2

師：很好.接下來請同學們完成第2個性質的證明.

已知：如圖2，在菱形ABCD中，對角線AC，BD相交于點O.求證：AC⊥BD.

學生自主完成證明過程，教師巡視指導證明的規范書寫，師生歸納出兩種方法：一是證明三角形全等；二是利用“等腰三角形三線合一”.師生通過比較，一致認為第2種方法更加簡潔.

追問1：利用“等腰三角形三線合一”還能得出什么結論？

追問2：你能通過折疊得到上述性質嗎？

追問3：菱形具有怎樣的對稱性呢？

最后由學生從邊、角、對角線以及對稱性方面對菱形的性質進行系統梳理.

設計意圖：通過折紙，引導學生從邊、角、對角線三個要素自主探究菱形的性質，明晰研究圖形性質的一般路徑，同時處理好特殊與一般的關系.通過進一步的證明，加強邏輯推理，體現數學的嚴謹性.

2.3 用——由“學以致用”到“舉一反三”

例題如圖2，在菱形ABCD中，對角線AC，BD相交與點O, ∠BAC=30°，BD=6，求菱形的邊長和對角線AC的長.

師生活動：由學生自主完成求解過程，教師指導規范求解過程，并作如下追問.

追問1：得出等邊三角形的依據是什么？

追問2：此例題用到了菱形的哪些性質？

設計意圖：例題是在前面圖形基礎上，對內角的特殊化，讓學生探究邊、角、對角線之間的一些結論，也是對菱形中特殊三角形挖掘的延續.

2.4 變——由“千變萬化”到“追本溯源”

練一練如圖3，已知菱形ABCD中，AE⊥BC，AF⊥CD，垂足分別為E,F.求證：AE=CF.

圖3

圖4

方法1：證△ABE≌△ADF可得AE=CF.

方法2：S菱形ABCD=BC·AE=CD·AF，再由BC=CD可得AE=CF.

變式1如圖4，已知菱形ABCD中，E,F分別是CB，CD上的點，且BE=DF.

求證：∠AEF=∠AFE.

方法1：證△ABE≌△ADF可得AE=AF，再由等腰三角形性質可證得結論.

方法2：連結AC，證CE=CF，再由“等腰三角形三線合一”可得.

圖5

變式2如圖5，在菱形ABCD中,∠ABC=60°.現將一塊含60°的三角尺AMN (其中∠NAM=60°)疊放在菱形上,然后將三角尺繞點A旋轉.在旋轉過程中,設AM交邊BC于點E,AN交邊CD于點F,那么BE+DF與AB有怎樣的數量關系?

分析：連結AC，證△ABE≌△ACF或△ACE≌△ADF，再由“菱形的四條邊都相等”可得.

追問：四邊形AECF與菱形ABCD的面積之間有何關系？

設計意圖：幾何教學應當進行適當的變式練習，體現“萬變不離其宗”的數學本質，追本溯源，揭示數學本質.以教材習題為基本素材，通過點E,F在菱形邊上的位置變化，進行變式訓練，加深學生對菱形性質的理解.

通過“問題驅動”的方式展開小結，從研究內容到研究方法的延伸，將本節課的知識脈絡清晰地展現在學生面前，內化整堂課所學內容，由“知識梳理”到“思維提升”的演變，為后續學習做好鋪墊.

3 教學反思與感悟

3.1 聚焦數學實驗，揭示數學本質

數學實驗教學，是讓學生通過動手操作，進行探究、發現、思考、分析、歸納等思維活動，最后獲得數學結論，它是讓學生內心生長的一種有效途徑.在本節課教學中，通過折紙，引導學生類比平行四邊形，自主探究菱形的性質.讓學生聚焦在折紙這個數學實驗上，去發現與經歷菱形的概念的形成與理解，有效地撬動學生的思維自然生長，理性思考，有助于在教和學中揭示數學本質.

3.2 挖掘數學內涵，提升學科素養

《義務教育數學課程標準(2011版)》在“課程設計思路”中明確指出：“在數學課程中應注重發展學生的幾何直觀與邏輯推理能力.”因此，指向數學本質的數學教學不能停留于知識層面，而是讓學生經歷深度學習的過程，促進思維的自然生長；引領學生去充分挖掘菱形的內涵；同時在教學中滲透轉化、類比的數學思想，積極培養學生的邏輯推理能力，進而提升數學學科素養[3].