基于分數階Tikhonov 正則化的激光吸收光譜燃燒場二維重建光路優化研究*

龐維煦 李寧 黃孝龍 康楊 李燦 范旭東 翁春生

(南京理工大學,瞬態物理國家重點實驗室,南京 210094)

為探究基于激光吸收光譜技術的燃燒場二維測量光路布置方式,實現有限投影下更精確的燃燒場二維重建,根據分數階微積分理論,提出一種基于分數階Tikhonov 正則化的光路優化方法.將經典的整數階Tikhonov 正則化推廣到分數階模式,建立了基于分數階Tikhonov 正則化的光路設計目標函數.利用遺傳算法分析(0,1)范圍內不同階數的計算結果,得到最佳光路布置方式.采用近紅外波段7185.6 cm–1 的H2O 特征吸收譜線結合20 條測試光路對10×10 離散化網格區域進行計算,對比分析五種光路布置方式對多種分布模型的重建結果,結果表明,基于分數階Tikhonov 正則化的光路布置方式具有最佳重建效果.研究結果對有限投影條件下激光吸收光譜二維測量光路的優化設計理論研究具有重要意義,可以促進激光吸收光譜技術在復雜發動機燃燒場二維重建及燃燒效率提升方面的應用.

1 引言

可調諧二極管激光吸收光譜技術(tunable diode laser absorption spectroscopy,TDLAS)作為一種非接觸測量手段,它通過穿過待測介質的激光束實現對流場溫度、組分濃度及速度等參數的在線監測,具有測量靈敏度高、抗噪聲干擾能力強、流場適用性強等優點,在發動機性能測試中發揮重要作用[1?4].受該技術的視線特性以及燃燒場不均勻分布的限制,需要結合斷層掃描技術對測量光路系統進行設計,實現對燃燒場組分濃度或溫度的二維分布測量,從而使TDLAS 技術更加廣泛應用在發動機燃燒診斷、工業過程控制、環境傳感測量等領域[5?8].

測量空間有限導致待測區域離散化網格數量遠遠大于測量系統可布置的光路數量.只有很少一部分離散化網格內有光線通過.由于“無光路”網格數量較多,光路投影角度不完備,且各角度下光路投影數目較少,燃燒場的二維重建屬于病態方程組求解問題.常采用迭代求解算法對該類問題進行迭代求解,如代數迭代算法、最大似然-期望最大化算法、最小二乘QR 分解算法等,或采用模擬退火算法、遺傳算法、Levenburg-Maquardt 算法等搜索算法迭代搜索最優解.但是這兩類算法往往因其局限性而不能得到很好的解,對后續重建工作帶來較大誤差.Tikhonov 正則化方法為此類問題的求解提供一個很好的思路,以適當正則化參數和正則化矩陣來控制方程解的平滑性,得到唯一正則解.Tikhonov 正則化策略可以得到較好的燃燒場參數分布情況,還可以結合截斷奇異值分解算法進行數學分析,截去引起解不穩定的小奇異值,降低原方程組病態性,提高原方程組解的穩定性.

TDLAS 光路系統的優化是燃燒場二維重建的關鍵,研究人員從不同角度展開了深入研究.平行光路[9?16]、扇形光路[3,12,17,18]是常見的規則TDLAS光路布置方式,但這兩類規則光路布置方式在有限的投影數量下對燃燒場的重建具有較大限制,無法保證重建精度.理論上,增加光路數量會提高燃燒場二維重建質量.但在實際測試中,光路數量往往受限于激光器數量及測試環境,從而影響規則TDLAS 光路布置方式的重建效果.

部分學者對不規則光路布置方式進行研究,進而提升有限投影數量下的激光吸收光譜二維重建能力.Terzija等[15]提出使用正弦圖幾何坐標對穿過發動機氣缸的27 條不規則成像光路進行優化,盡管他們進行了定量重建實驗,但文中對于該方法的數學理論分析提及較少.宋俊玲等[19]定義每個離散網格內穿過的光路數量為權值因子,以溫度場重建結果均方誤差作為光路分布的優化標準,并通過數值模擬驗證了不規則光路布置方式的重建性能.Tsekenis等[20]尋找光路優化的“無觀察者”特征,得到最小空間分辨率,為TDLAS 光路布置方式的優化提供了一個較好的思路.Yu等[21]以最小化矩陣向量正交度建立優化函數,不斷減小投影光路相關性,使光路可以攜帶更多測量數據.根據宋俊玲等[22]提出的虛擬光線重建方法,那奕君等[23]采用不規則光路布置方式,以多角度再投影對病態方程組進行二次求解,提高了二維重建精度.Grauer等[24]基于Bayesian 原理提出估計后驗協方差矩陣的光路優化方法,結合單一正則化參數的Tikhonov正則化推導出光路優化目標函數表達式,仿真結果表明該方法可以衡量二維重建誤差.Twynstra 和Daun[25]依據Tikhonov 正則化理論,推導出基于單一正則化參數的光路設計函數.根據光路矩陣奇異值分布判斷正則化參數的選取范圍,并通過數值模擬驗證了該方法的正確性.李寧等[26]提出基于Tikhonov 正則化參數矩陣的TDLAS 光路優化算法,理論推導出光路設計函數,采用遺傳算法獲得優化后的光路布置方式.該算法采用正則化參數矩陣調節正則解的平滑度,但在優化過程中還需要更加注意方程解的數據細節.

有限投影數據很難精確重建燃燒場,因此基于Tikhonov 正則化方法的光路系統在優化過程中更應關注方程組解的細節信息.本文提出一種基于分數階Tikhonov 正則化的燃燒場二維重建光路設計方法,引入階數改善了正則解過于平滑的缺點,在系數矩陣奇異值的保留上進行優化,進一步提高重建質量.理論推導出分數階Tikhonov 正則化光路設計函數,通過遺傳算法選擇最佳階數,得到最佳光路布置方式.通過對不同模型及不同光路對比分析,驗證基于分數階Tikhonov 正則化設計的光路布置方式的重建效果.該方法可為基于TDLAS技術的燃燒場重建光路設計提供一定理論求解思路,對復雜燃燒場二維重建具有重要的理論研究意義和工程應用前景.

2 TDLAS 光路設計方法

2.1 標準Tikhonov 正則化二維重建原理分析

可調諧激光器發射出波長為ν的激光穿過待測氣體區域,激光能量被氣體吸收并產生衰減效應,其規律滿足Beer-Lambert 定律:

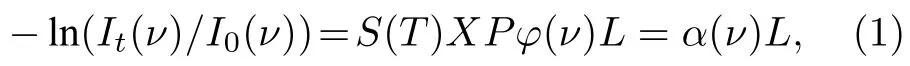
其中I0與It為激光穿過待測氣體前后的強度;ν為波長;X為待測區域氣體體積濃度;L為激光在均勻氣體介質中的傳播長度;P為待測區域氣體總壓力;α(ν)為氣體吸收系數;φ(ν)為吸收譜線線型函數;S(T)為吸收譜線的線強函數,表示氣體對光強吸收的強弱程度.圖1 所示為TDLAS 測量及重建示意圖.

圖1 TDLAS 測量及重建示意圖Fig.1.Schematic diagram of TDLAS measurement and reconstruction.

在不同角度及位置布置測試光路,可以得到大量投影數據,實現燃燒場的二維診斷.將待測區域離散化,得到n個網格.假定每個網格內部的氣體溫度均勻分布,通過疊加每個網格內部的氣體吸收貢獻值從而得到氣體吸收系數.(1)式的離散化形式可以表示為

其中Aij為第i條光路在第j個網格內的光程長度;xj為第j個網格內的吸收系數;bi為第i條光路測量得到的投影值,為光譜系數累積值.對于含有m條光路的測試系統,燃燒場二維重建的關鍵是求解如下矩陣方程組:

其中A為m×n階吸收系數矩陣,x為n×1 階未知數向量,b為m×1 階投影向量.實際的燃燒場二維重建因測量空間有限,光路數m遠小于網格數n,因此TDLAS 二維重建屬于病態方程組求解問題.

Tikhonov 正則化是求解病態方程組的有效辦法之一,它通過增加約束條件使(3)式的解存在且唯一.此時將方程組求解問題轉化為求最小值問題:

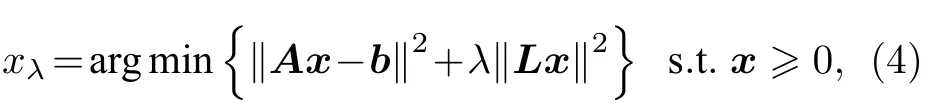
其中λ為正則化參數,用于控制殘差范數與解向量范數的平衡;L為n×n階正則化矩陣,常為單位陣或1 階微分算子.考慮到燃燒場為連續分布,因此本文中正則化矩陣L采用微分算子形式:

其中k為與第i個網格相鄰的網格數.

通過數學推導,(4)式的最小化問題等價于求如下正則化線性方程組的解:

因為方陣ATA為半正定矩陣,且正則化參數λ非零,(6)式的解可以表示為

2.2 基于分數階Tikhonov 正則化的光路設計原理

對于標準Tikhonov 正則化,通常情況下其正則解xλ會表現的過于光滑,即解向量經去噪處理后丟失了許多含有較小奇異值的數據細節[27].針對這一不足,Hochstenbach 和Reichel[28]根據分數階微積分理論思想,提出一種分數階Tikhonov 正則化方法.本文將該方法應用于燃燒場二維重建光路設計,將(3)式轉化為如下最小值問題:

其中參數α為分數階次,選擇合適的α值可以提高(8)式中解的質量.當α=1 時為標準Tikhonov正則化,此時W為單位陣.

通過數學推導,(8)式的分數階Tikhonov 正則化最小值問題可以得到如下正態方程:

由于矩陣ATA為半正定矩陣,通過數學計算后,(10)式的正則解可以表示為

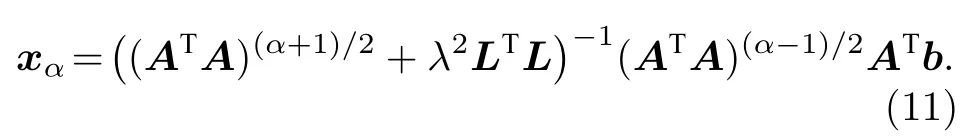
2.3 基于分數階Tikhonov 正則化光路設計方法及求解

分析正則解xα與精確解x*之間的誤差δx,進一步得到:

其中I為單位矩陣.可以看出,影響誤差δx的直接因素是系數矩陣A、正則化參數λ及階數α.通過合理設計光路結構與恰當選擇參數,可有效地減小誤差δx.為了進一步討論光路結構與激光吸收光譜二維重建的關系,本文定義F為光路設計目標函數:

為了優化光路布置方式,需要對非線性方程(13)進行求解.遺傳算法是基于生物進化理論的自主尋優算法,以目標函數值作為搜索信息,從具有多個個體的初始群體出發,有效地搜索非必要點,能夠得到較為準確的全局解.(13)式中正則化參數λ與階數α均為固定常數.所有參數選定并固定后,光路設計目標函數F的變化僅與系數矩陣A有關,而系數矩陣A是由光路布置方式所決定,因此非線性方程(13)的最優解對應最優的光路布置方式.本文采取遺傳算法對方程(13)進行最優值求解.圖2 所示為遺傳算法求解最優值的流程框圖.

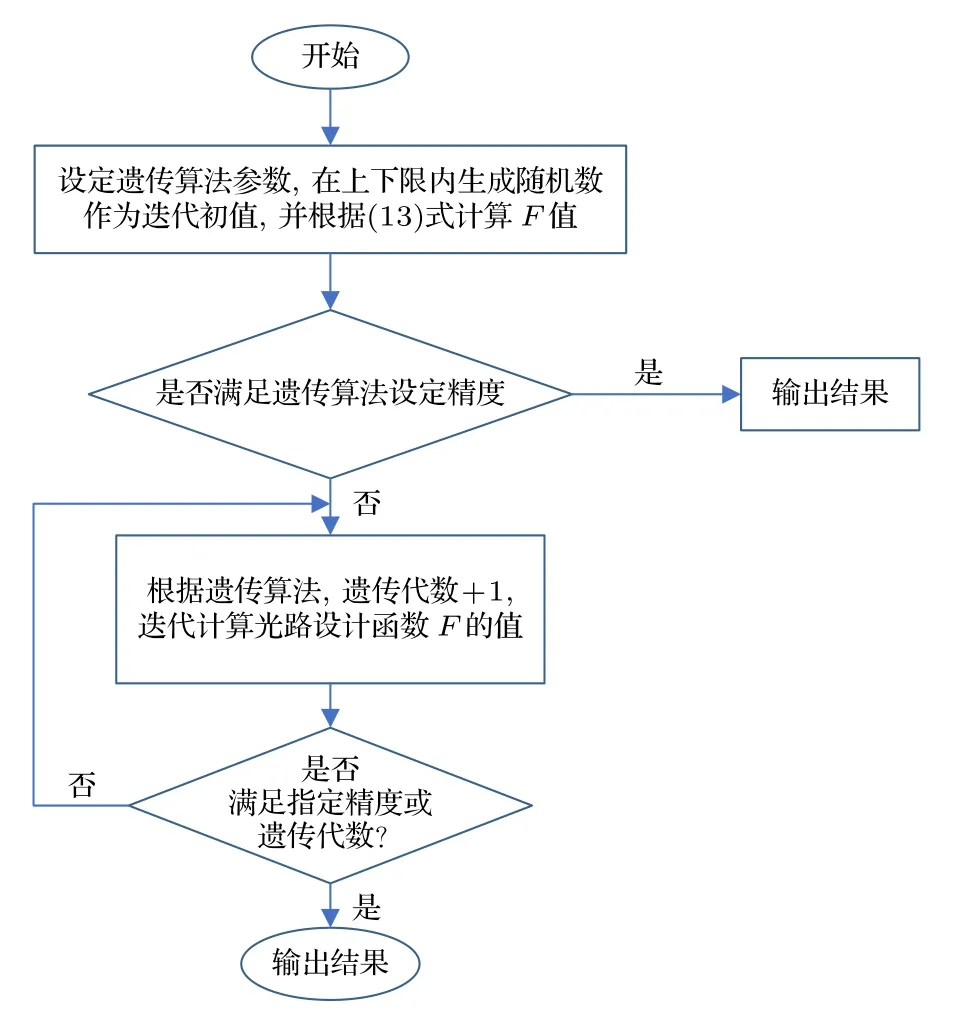
圖2 遺傳算法求解流程框圖Fig.2.Flow chart of genetic algorithm.

本文采用遺傳算法對20 條光路求解計算.將目標區域離散化為10×10 網格,以每條光路距離中心的距離及角度弧度值作為未知數,以上下限內的隨機數作為初始種群,求解光路設計函數方程(13)每一代的最小值.遺傳代數設定為2000 代,迭代完成后,輸出最終的F值作為該光路設計函數的最優值進行保留.F值越小代表正則解越接近初始解,后續重建效果也更好.

2.4 階數α 取值范圍的選擇

選定正則化參數矩陣L與正則化參數λ后,還需要確定階數α的取值范圍.

對投影矩陣A進行奇異值分解(SVD),可得

其中UA,VA為左右奇異向量列矩陣;ΣA為矩陣A的奇異值σi所組成的對角矩陣.將(14)式代入(10)式,可以得到分數階Tikhonov 正則化解的表達形式為

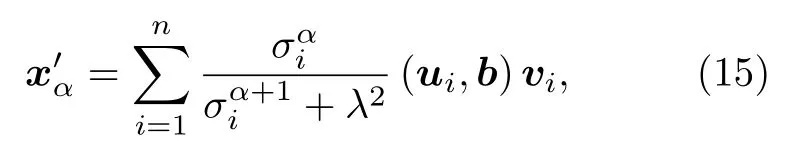
其中(ui,b)表示向量ui與b的內積;ui,vi分別為正交陣UA,VA的列向量.

不同正則化方法有不同濾波函數,濾波函數的收斂情況與解向量的平滑程度緊密相關.定義分數階Tikhonov 正則化方法的濾波函數為

分析上述濾波函數的漸近性,可以得到

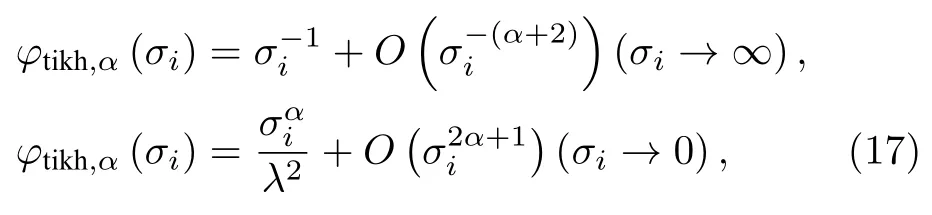
其中O(·)表示高階無窮小量.由(17)式可以看出,當矩陣A的奇異值逐漸趨于0 時,濾波函數φtikh,α(δi)也逐漸趨向于0,而φtikh,α(δi)收斂過快是解向量過于光滑的原因.圖3 為奇異值在10–11至103時濾波函數隨階數α變化的曲線圖.

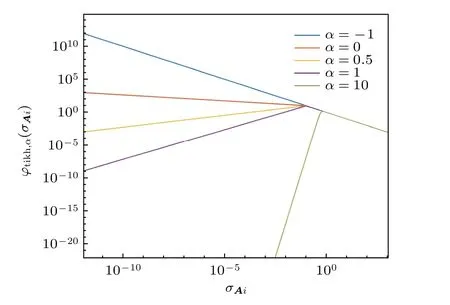
圖3 濾波函數隨階數α 的變化Fig.3.Variation of filter function withα order.

由圖3 可知,當α取值大于1 時,濾波函數收斂較快,使得方程組的解過于光滑,導致丟失了許多小奇異值關聯的奇異向量,而這些向量反映的是重建數據的細節.當α取負數時,濾波函數在很大奇異值范圍內單調遞減,表明其去噪能力過弱,導致正則解收斂性較差或不收斂,對后續二維重建帶來較大誤差.由此說明階數α的最佳取值范圍為(0,1).從濾波函數的漸近性可以看出,相比于標準Tikhonov 正則化,分數階Tikhonov 正則化收斂速度更慢,即較小奇異值對應的分量被有效保留下來.因此選擇0<α<1,濾波函數可以提供更合適的平滑度,(10)式得到的解的質量會高于標準Tikhonov 正則化.綜上所述,在(0,1)范圍內選擇合適的階數α,可以有效地保留小奇異值對應的奇異向量,抑制較大奇異值對應的分量,提高解向量xα范數而逼近精確解,使方程組的解可以攜帶更多有效信息,重建結果更精確.

2.5 正則化參數λ 的選擇

正則化參數λ的選擇對燃燒場的二維重建效果具有重要影響.本文的正則化矩陣L非單位陣,因此不能通過L曲線法等方法確定λ的具體取值.

為了更準確地選取正則化參數λ,本文在不同階數α取值時對光路設計函數(13)式進行遺傳算法迭代分析,由迭代結果選取最佳的正則化參數λ.本文以10×10 離散化網格,20 條光路測試系統為研究對象,圖4 為不同階數下不同正則化參數的1000 代遺傳算法求解結果.

從圖4 可以看出,當階數α取不同值時,正則化參數λ取1 或0.1 時可以帶來更小的光路優化函數值.當正則化參數λ取102時,不同階數下光路優化函數F的值均很大,且很快達到穩定狀態,表明過大的正則化參數λ會使正則化的作用過于明顯,正則解過于平滑.當正則化參數λ取較小的值時,正則解的平滑程度得到控制,但過小的正則化參數λ仍不能得到光路優化函數F的最小值,會帶來較大的重建誤差.綜合考慮,正則化參數λ的最優取值范圍為(0.1,1),因此本文后續的重建效果對比中,λ取0.5.

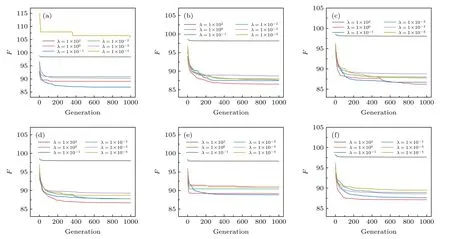
圖4 不同階數下正則化參數取值對遺傳算法結果的影響(a)α=0.2;(b)α=0.4;(c)α=0.5;(d)α=0.6;(e)α=0.8;(f)α=1.0Fig.4.Influences of regularization parameters on the genetic algorithm results under different orders:(a)α=0.2;(b)α=0.4;(c)α=0.5;(d)α=0.6;(e)α=0.8;(f)α=1.0.

圖5 所示為遺傳算法對光路設計函數(13)式求解的最優值變化過程,以及對應的光路布置方式圖像.

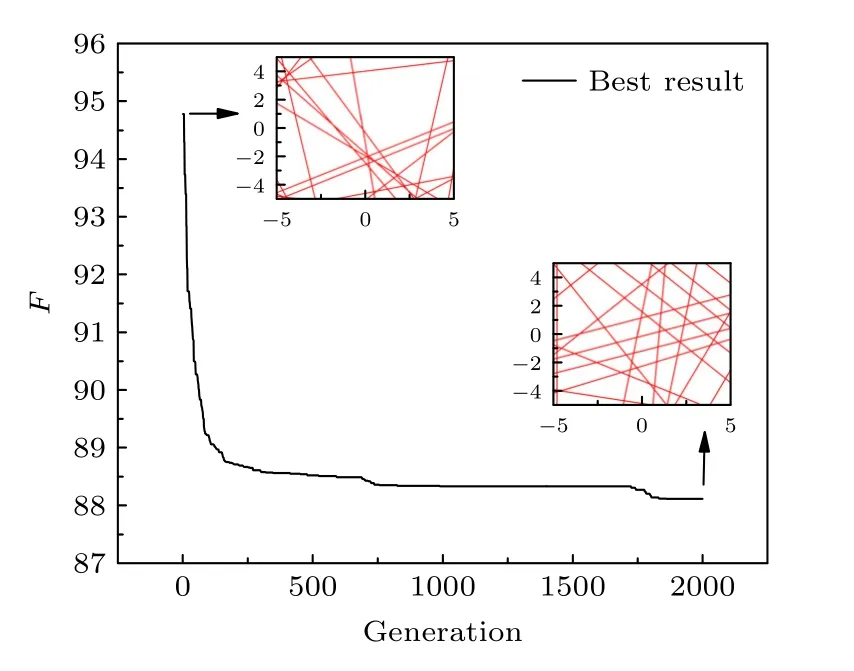
圖5 光路優化函數的遺傳算法求解Fig.5.Genetic algorithm solution for beam optimization function.

分數階Tikhonov 正則化可以得到較好的光路布置方式,進而計算得到燃燒場的溫度與濃度分布情況.本文的研究重點為利用分數階Tikhonov 正則化方法得到有限投影下的光路系統,評估該光路系統的重建效果.為了更好地比較重建結果,以網格吸收系數為指標對重建圖像質量進行對比分析.定義吸收系數平均相對誤差ε,用來描述重建結果與初始模型之間對應網格內數據的平均差異:

式中,N為離散化網格數目,為模型吸收系數,為計算得到的吸收系數.誤差ε值越小,表明重建圖像與初始模型匹配度越高,重建質量越高.

3 TDLAS 二維重建仿真

3.1 分數階α 的取值選擇

分數階Tikhonov 正則化方法的實質是:通過階數控制投影方程計算精度,選擇階數α以提高方程組解xα范數,進一步逼近方程組的精確解,提高光路優化函數的求解精度.根據(13)式可知,系數矩陣A的奇異值會直接影響重建光路的布置方式,因此在(0,1)范圍內選擇合適的階數,以該階數對應光路為最優光路布置方式,進一步提升重建效果.

為了進一步分析階數α的取值及作用,以20 條光路,10×10 離散化網格為例進行討論.在(0,1)范圍內選取五個α值,α=1.0 時為標準Tikhonov 正則化.圖6 所示為光路優化函數的遺傳算法求解.

由圖6 可以明顯地看出,當α=0.4 時,光路優化函數的遺傳算法求解結果最小,此時最小的F值對應(10)式的最優解,也對應(8)式的最小值.因此,選擇α=0.4 作為最佳階數,可以更好地保留方程組精確解的有效信息,重建質量得到提升,同時選擇該階數對應的光路進行后續不同光路重建效果的對比分析.

圖6 不同階數取值下的光路優化函數求解Fig.6.Solution of beam optimization function under different order values.

3.2 分數階α 取值的影響因素分析

研究不同網格尺寸對分數階Tikhonov 正則化階數取值的影響.系數矩陣A的奇異值會隨著測量區域尺寸的增大而增大,正則化參數λ的值也應隨之變化.以上文α=0.4 為最優階數,保持該階數固定不變,改變正則化參數λ的值,以改變正則項在(10)式中的比重,實現(13)式更精確的求解.

以1 m 網格為基準,當網格邊長縮小至0.1 m時,正則化參數的最優取值區間由0.1 至1 縮小為0.01 至0.1.當網格邊長擴大至10 m 時,正則化參數的最優取值區間擴大為1 至10.因此可以認為當網格尺寸發生變化時,只需將基準正則化參數λ與測量區域尺寸相乘,從而保證最終階數的選擇不變.在此基礎上,光路設計函數(13)式可以等價為如下形式:

其中λα為固定常數,以1 m 測量區域尺寸的取值為標準;l為測量區域網格的邊長.當λα固定時,階數α的取值不會發生改變,當λα變化時,階數α的取值會發生改變.

另外,測量區域的尺寸恒定時,加密網格或增加光路數量基本不會改變系數矩陣A的奇異值,正則化參數λ的取值不會隨之發生變化,因此,不會影響階數α的取值.

3.3 基于分數階Tikhonov 正則化的光路設計與重建效果對比

根據分數階微積分理論,利用分數階Tikhonov正則化方法得到燃燒場重建的光路設計函數,結合遺傳算法可以得到優化后的激光吸收光譜二維測量光路布置方式.為驗證該光路布置方式的重建效果,分別與以下光路布置方式得到的重建結果進行對比:方式(a)2×10 正交光路布置方式;方式(b)4×5 扇形光路布置方式;方式(c)交叉光路布置方式;方式(d)基于標準Tikhonov 正則化設計的光路布置方式;方式(e)基于分數階Tikhonov 正則化設計的光路布置方式.圖7 所示為不同光路布置方式的分布情況及其極坐標投影點.

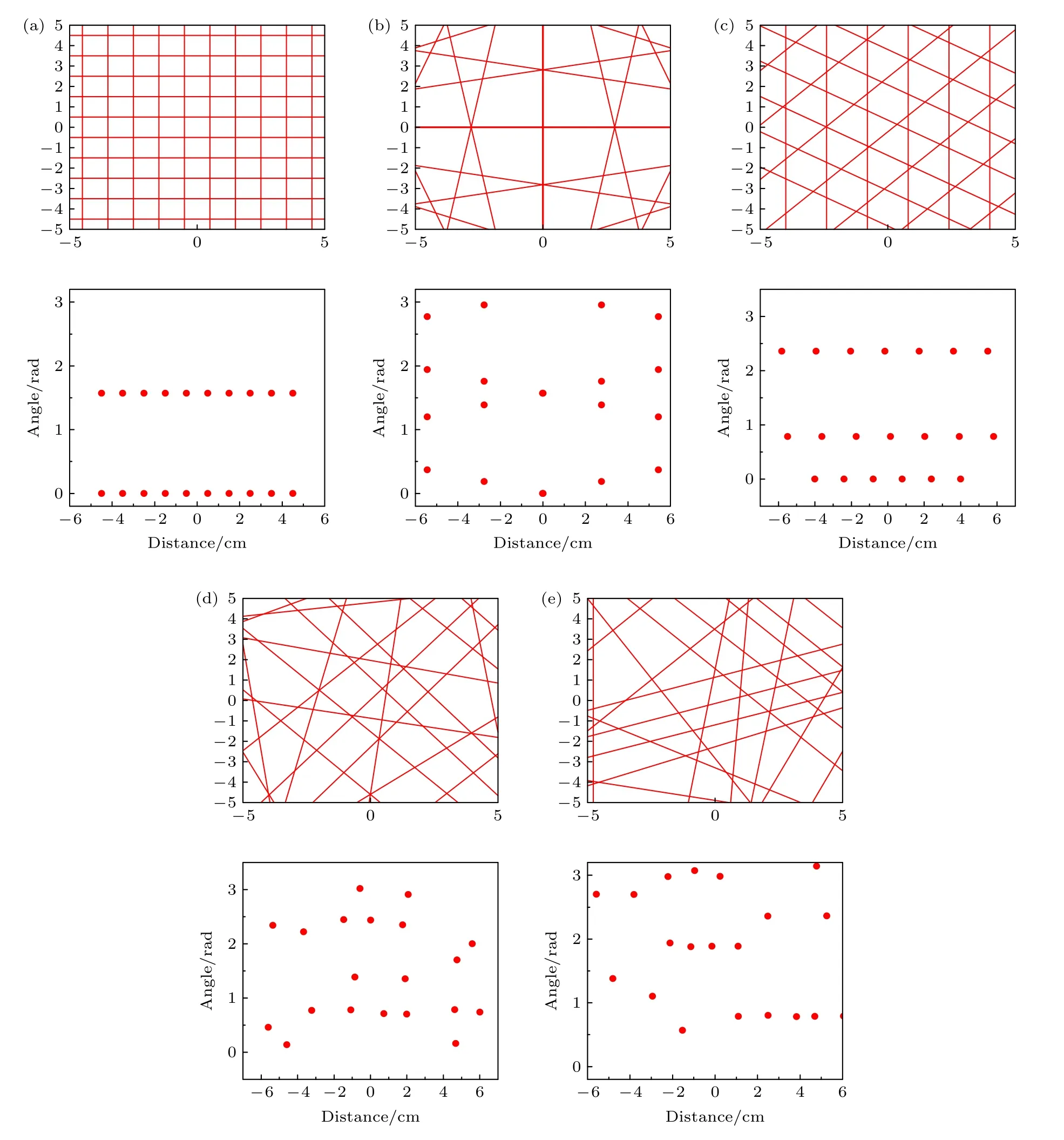
圖7 五種光路布置方式的空間分布圖與投影點分布圖(a)2×10 正交光路布置方式;(b)4×5 扇形光路布置方式;(c)交叉光路布置方式;(d)基于標準Tikhonov 正則化設計的光路布置方式;(e)基于分數階Tikhonov 正則化設計的光路布置方式Fig.7.Spatial distribution and projection point distribution diagram of five beam arrangements:(a)2×10 orthogonal optical path arrangement;(b)4×5 fan-shaped optical path arrangement;(c)cross optical path arrangement;(d)beam arrangement based on standard Tikhonov regularization design;(e)beam arrangement based on fractional Tikhonov regularization design.

選取不同高斯模型為研究對象,討論不同光路布置方式在不同模型下的重建結果.將測量區域離散化為10×10 網格,選擇燃燒場中的H2O為測量對象,選擇其近紅外波段7185.6 cm–1處的特征吸收譜線為測量譜線,重建模型分別采用單峰高斯分布模型與雙峰高斯分布模型,光路數量均為20 條.為控制變量,圖7 中的光路布置方式均使用相同正則化參數(λ=0.5)下的標準Tikhonov正則化方法,直接計算得到重建結果.圖8 與圖9為不同重建模型及不同光路布置方式下的重建結果圖.

圖8 單峰分布模型與不同光路布置方式的重建結果圖(a)重建模型;(b)2×10 正交光路布置方式;(c)4×5 扇形光路布置方式;(d)交叉光路布置方式;(e)基于標準Tikhonov 正則化設計的光路布置方式;(f)基于分數階Tikhonov 正則化設計的光路布置方式Fig.8.Reconstruction results of unimodal distribution model and different beam arrangements:(a)reconstruction model;(b)2×10 orthogonal beam arrangement;(c)4×5 fan-shaped beam arrangement;(d)cross beam arrangement(e)beam arrangement based on standard Tikhonov regularization design;(f)beam arrangement based on fractional Tikhonov regularization design.

圖9 雙峰分布模型與不同光路布置方式的重建結果圖(a)重建模型;(b)2×10 正交光路布置方式;(c)4×5 扇形光路布置方式;(d)交叉光路布置方式;(e)基于標準Tikhonov 正則化設計的光路布置方式;(f)基于分數階Tikhonov 正則化設計的光路布置方式Fig.9.Reconstruction results of bimodal distribution model and different beam arrangements:(a)Reconstruction model;(b)2×10 orthogonal beam arrangement;(c)4×5 fan-shaped beam arrangement;(d)cross beam arrangement;(e)beam arrangement based on standard Tikhonov regularization design;(f)beam arrangement based on fractional Tikhonov regularization design.

從圖8 可以看出,對于單峰分布模型,不同光路布置方式得到的重建結果存在差異.光路布置方式(a)和方式(b)的重建結果相比其他方式的重建

結果較差,峰值位置與模型相同,但峰值大小存在明顯偏差,重建誤差分別為0.0974 和0.0633,且在吸收系數較小的區域重建誤差更大,如圖8(b)和圖8(c)所示.光路布置方式(c)在光路布置方式(a)的基礎上增加了投影角度,相比前兩種方式,該方式的重建質量明顯提升,誤差為0.0503,但重建圖像的峰值大小相比原模型依舊存在較大誤差,如圖8(d)所示.光路布置方式(d)和光路布置方式(e)得到的重建結果很好,重建結果的峰值位置和峰值大小均與原模型基本吻合,重建誤差分別為0.0307 與0.0236,但是與重建模型相比,光路布置方式(d)和光路布置方式(e)得到的重建結果在模型邊界處依然會有一些網格存在誤差(圖中黑色部分所示),如圖8(e)和圖8(f)所示.

從圖9 可以看出,對于雙峰分布模型,不同光路布置方式對應的重建結果具有較大差異.光路布置方式(a)的重建結果最差,峰值位置與峰值大小均與原模型有較大偏差,重建誤差達到了0.0485,如圖9(b)所示.方式(a)的正交光路雖然能夠保證每個網格內部均有光線通過,但投影角度過少,相鄰光線距離過近是其重建誤差較大的原因.后四種光路布置方式均能夠重建得到較準確的峰值位置.光路布置方式(b)的重建誤差為0.0411,重建結果如圖9(c)所示.扇形光路增加了投影角度,但相鄰的光線會重復穿過同一個網格,因此重建誤差也較大.對于光路布置方式(c)而言,該方式將方式(a)改為三角度投影,重建結果如圖9(d)所示,重建誤差為0.0387,可見重建質量相比于方式(a)有了較大提升,但重建峰值大小相比原模型依舊存在較大誤差.這是由于方式(c)的投影角度增加,每個投影角度上的光線數量減少且相鄰平行光線之間的距離增加.但該光路布置方式的光路利用率較低,因此需要選擇利用率更高的光路布置方式來提高重建精度.

基于標準Tikhonov 正則化的光路布置方式(d)和基于分數階Tikhonov 正則化的光路布置方式(e)對應的重建結果較好,重建得到的圖像峰值位置與原模型較為吻合,峰值大小更接近原模型,二者的重建誤差分別為0.0336 與0.0228,如圖9(e)和圖9(f)所示.相比之下,基于分數階Tikhonov正則化的光路布置方式得到的重建效果更加理想.該方法在標準Tikhonov 正則化的基礎上,在AAT的偽逆中引入階數α可以有效地保留投影矩陣較小的奇異值,使計算得到的光路數據能夠盡可能多地攜帶精確解的細節信息,從而降低正則解的平滑性,達到更好的重建效果.

以四峰高斯分布模型為例,驗證基于分數階Tikhonov 正則化設計的光路布置方式對復雜燃燒場的重建能力.分別采用上述五種光路布置方式對其進行重建,重建結果表明,基于分數階Tikhonov正則化設計的光路布置方式的重建能力最好,重建誤差為0.0415.雖然重建結果中有個別網格內的數據存在偏差,但重建結果依然能夠較為準確地反映燃燒場模型中的峰值數量和峰值位置.因此在實際復雜燃燒場工況下,基于分數階Tikhonov 正則化設計的光路布置方式依然可以提供有效的燃燒場重建結果,從而對燃燒狀態進行診斷.

4 結論

實現不完備投影數據下燃燒場二維重建的關鍵是光路布置方式的優化.本文基于激光吸收光譜技術,采用分數階Tikhonov 正則化方法對燃燒場投影病態方程組進行求解,獲得最優光路布置方式.為解決采用標準Tikhonov 正則化方式得到的正則解過于光滑這一問題,提出了一種基于分數階Tikhonov 正則化方法的光路優化思路,通過數學推導建立光路優化函數,采用遺傳算法分析得到優化后的光路布置方式.分析了分數階數的作用效果,表明分數階Tikhonov 正則化方法可以通過選擇合適的階數來提高重建精度.利用基于分數階Tikhonov 正則化方法的光路布置方式與其他光路布置方式分別對不同高斯分布模型進行重建效果對比,結果表明本文設計的光路布置方式的重建精度最高,能夠達到更好地重建效果.研究結果對有限投影條件下的激光吸收光譜技術二維重建技術理論研究具有重要意義,為激光吸收光譜二維重建技術在燃燒診斷領域的實際化應用提供技術支撐.