鈦合金型面?zhèn)缺阢娤髁Ec仿真*
李安海 朱曉麗 張茹鳳 蓋少磊
(①山東大學(xué)機(jī)械工程學(xué)院高效潔凈機(jī)械制造教育部重點(diǎn)實(shí)驗(yàn)室,山東 濟(jì)南 250061;②機(jī)械工程國(guó)家級(jí)實(shí)驗(yàn)教學(xué)示范中心(山東大學(xué)),山東 濟(jì)南 250061;③德州大陸架石油工程技術(shù)有限公司,山東 德州 253034;④濱州渤海活塞有限公司,山東 濱州 256602)
鈦合金由于高強(qiáng)度重量比和好的耐腐蝕性能等性能特點(diǎn),廣泛應(yīng)用于航空航天等領(lǐng)域,而鈦合金復(fù)雜整體結(jié)構(gòu)零件通常由側(cè)壁、腹板和不規(guī)則框架組成,材料去除量大且因受力情況難以控制容易產(chǎn)生彈性變形[1]。特別是側(cè)面壁板型面結(jié)構(gòu)加工過程中,由于銑削力的作用下會(huì)產(chǎn)生“讓刀變形”,從而影響加工過程的穩(wěn)定性及加工表面質(zhì)量[2]。因此,需對(duì)鈦合金型面?zhèn)缺阢娤髁M(jìn)行有針對(duì)性地研究,從而控制鈦合金薄壁件或型面結(jié)構(gòu)件銑削加工變形。
切削力不僅會(huì)對(duì)表面粗糙度、加工硬化程度、殘余應(yīng)力和微觀結(jié)構(gòu)等加工表面質(zhì)量特征參數(shù)產(chǎn)生不可忽視的影響[3],還會(huì)嚴(yán)重地加劇刀具的磨損程度導(dǎo)致其使用壽命有所縮短[4]。銑削力建模研究可以有效預(yù)報(bào)切削加工過程銑削力,有助于更好地理解金屬材料加工機(jī)理。周鑫等人[5]提出了針對(duì)復(fù)雜結(jié)構(gòu)件特征的切削力建模預(yù)測(cè)方法,從而實(shí)現(xiàn)包含工件局部形狀尺寸和切削參數(shù)等信息的側(cè)銑切削力快速預(yù)測(cè)和評(píng)價(jià)。岳彩旭等人[6]采用Abaqus有限元仿真分析了刀具結(jié)構(gòu)參數(shù)對(duì)鈦合金薄壁件的銑削力的影響,并采用切削試驗(yàn)進(jìn)行了驗(yàn)證。趙仲林和安立寶[7]通過對(duì)比有限元仿真和BP神經(jīng)網(wǎng)絡(luò)對(duì)銑削力的預(yù)測(cè)值,證明了BP神經(jīng)網(wǎng)絡(luò)具有較高的預(yù)測(cè)精度。王海艷等人[8]基于斜角切削的切削力系數(shù)辨識(shí)方法,建立了考慮槽側(cè)刃和底刃的鈦合金螺旋銑孔切削力模型,并驗(yàn)證了斜角切削系數(shù)辨識(shí)方法的有效性。
通過切削力的預(yù)測(cè)建模,可以估算切削過程中的受力情況,為切削參數(shù)范圍的合理選擇與工藝方案的制定提供了理論依據(jù)。
本文基于機(jī)械力學(xué)理論并結(jié)合切削試驗(yàn),建立了四刃圓柱螺旋立銑刀的瞬態(tài)銑削力模型,最后借助于鈦合金側(cè)面?zhèn)缺阢娤髟囼?yàn)驗(yàn)證了所建立的切削力預(yù)測(cè)模型的可靠性。
1 整體立銑刀銑削力建模
整體立銑刀銑削力機(jī)械力學(xué)建模具體過程是,首先將銑刀切削刃沿其豎直軸線方向分割成若干個(gè)的切削微元,其分解幾何示意圖如圖1所示,繼而建立起切削微元(i,j)的各向切削力模型,對(duì)其進(jìn)行矢量求和后,通過數(shù)值積分和坐標(biāo)變換,即可進(jìn)一步確定出銑刀在旋轉(zhuǎn)一周時(shí)所受的X、Y和Z三個(gè)方向的整體切削力Fx(?)、Fy(?)、Fz(?)。
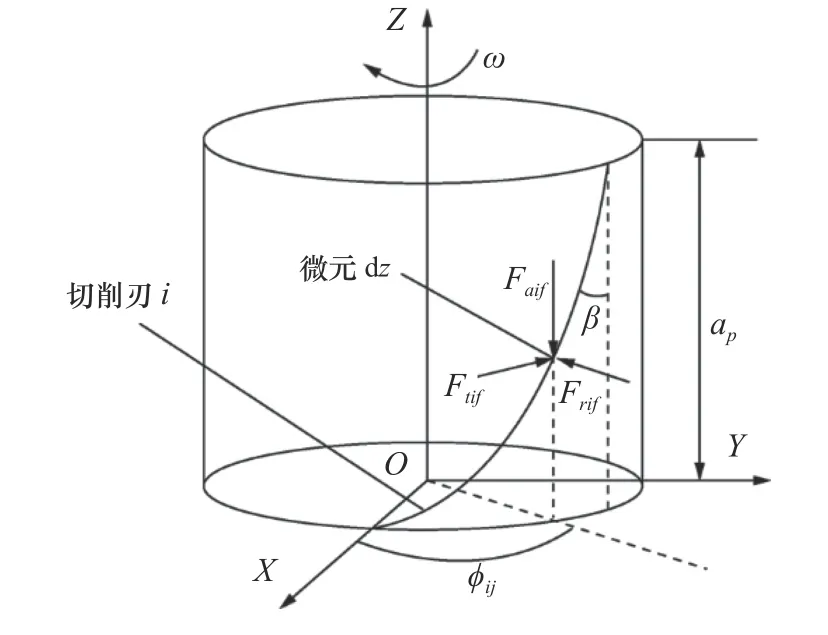
圖1 立銑刀切削刃微元分解幾何示意圖
對(duì)于刀具為四刃圓柱螺旋立銑刀,當(dāng)機(jī)床主軸帶動(dòng)刀具旋轉(zhuǎn)參與切削時(shí),由于螺旋角的存在,切削刃在軸線方向上相對(duì)于底刃有一個(gè)滯后角,則立銑刀半徑為R,螺旋角為β,則切深方向高度z處的瞬時(shí)切削角 ?i,j(z)的表達(dá)式為式(1)。
式中:?1為刀齒的接觸角;?p為立銑刀的刀齒齒間角,?p=2π/N,N為齒數(shù);i為銑刀的第i個(gè)切削刃;j為第i個(gè)切削刃上沿刀具軸線方向的第j個(gè)切削微元。其中,滯后角 ?r(z)為
每齒進(jìn)給量為fz時(shí),切屑厚度h在切削過程中會(huì)隨切削位置的改變而不斷改變,可表示為
由瞬態(tài)切削力模型的基本計(jì)算公式可知,切削微元(i,j)切向、徑向和軸向切削分力dFt、dFr和dFr可以分別表示為
式中:Ktc、Krc和Kac分別為切向、徑向和軸向的剪切力系數(shù),Kte、Kre和Kae分別為切向、徑向和軸向的刃口犁耕力系數(shù)。
如果要判別銑刀在某一瞬間對(duì)于任意一微元切削刃是否在參與切削,可由g(?i,j(z))斷定,其基本原理是根據(jù)瞬時(shí)切削角 φi,j(z)的位置來判別,也就是說當(dāng)其瞬時(shí)切削角和切入角?st及切出角?ex是否滿足條件?st≤?≤?ex。
順銑時(shí)
由銑刀各切削刃微元的空間位置基于坐標(biāo)變換即可獲得各方向切削力分量表達(dá)式。
將其沿軸線方向積分,然后將施加在各切削刃微元上的受力進(jìn)行整體矢量求和,刀具在旋轉(zhuǎn)參與切削時(shí)任意時(shí)刻整個(gè)立銑刀上的切削合力為
2 整體立銑刀銑削力系數(shù)辨識(shí)
切削力系數(shù)最常采用的求解方式主要分為兩種,一是基于斜角切削原理,根據(jù)刀具基本參數(shù)和幾何角度變換來計(jì)算金屬材料銑削加工的切削力系數(shù)[8],由于這種計(jì)算方法需要預(yù)先假定一些加工外部條件,使用范圍不可避免具有局限性,故而幾何求解模型的計(jì)算精度往往難以保證。另一種方法就是通過實(shí)驗(yàn)的方式來確定[9]。該方法主要是在保證其他參數(shù)值不變的前提下,只對(duì)每齒進(jìn)給量的數(shù)值做出調(diào)整,然后設(shè)置多組鈦合金切削試驗(yàn),進(jìn)而對(duì)一個(gè)周期內(nèi)平均銑削力的數(shù)值求解。在之前大多數(shù)研究中,常常較多地采用實(shí)驗(yàn)方法確定切削力系數(shù)數(shù)值。
銑刀的各個(gè)刀齒在單位切削時(shí)間內(nèi)試驗(yàn)中去除鈦合金工件材料的體積是固定不變的,因此螺旋角β的大小對(duì)銑刀平均切削力的數(shù)值大小沒有影響,因此在基于試驗(yàn)確定切削力系數(shù)數(shù)值時(shí)可以首先初步假定β=0°。因此在銑刀旋轉(zhuǎn)一周內(nèi)每個(gè)刀齒上的平均切削力F可以用銑刀整體切削力與刀具齒間角的比值計(jì)算求得,其數(shù)學(xué)表達(dá)式可表示為
則在圓柱立銑刀旋轉(zhuǎn)一周內(nèi)4個(gè)刀齒上各方向平均切削力數(shù)學(xué)計(jì)算表達(dá)式可表示為
其中:
因而各方向平均切削力試驗(yàn)值和每齒進(jìn)給量fz兩者之間的數(shù)學(xué)計(jì)算表達(dá)式可表示為
式中:各平均銑削分力值可以借助于鈦合金銑削力辨識(shí)試驗(yàn)來求取,然后使用Matlab軟件對(duì)各平均切削分力進(jìn)行數(shù)值線性擬合,獲得式(11)中變量值,繼而即可獲得鈦合金側(cè)銑試驗(yàn)圓柱螺旋立銑刀各切削力系數(shù)的數(shù)學(xué)計(jì)算表達(dá)式為
基于Matlab軟件編寫了四刃整體硬質(zhì)合金立銑刀瞬時(shí)切削力仿真程序,輸入切削參數(shù)、刀具參數(shù)和切削力系數(shù)等基本條件即可計(jì)算任意參數(shù)下圓柱螺旋立銑刀的瞬時(shí)切削力,程序流程見圖2。
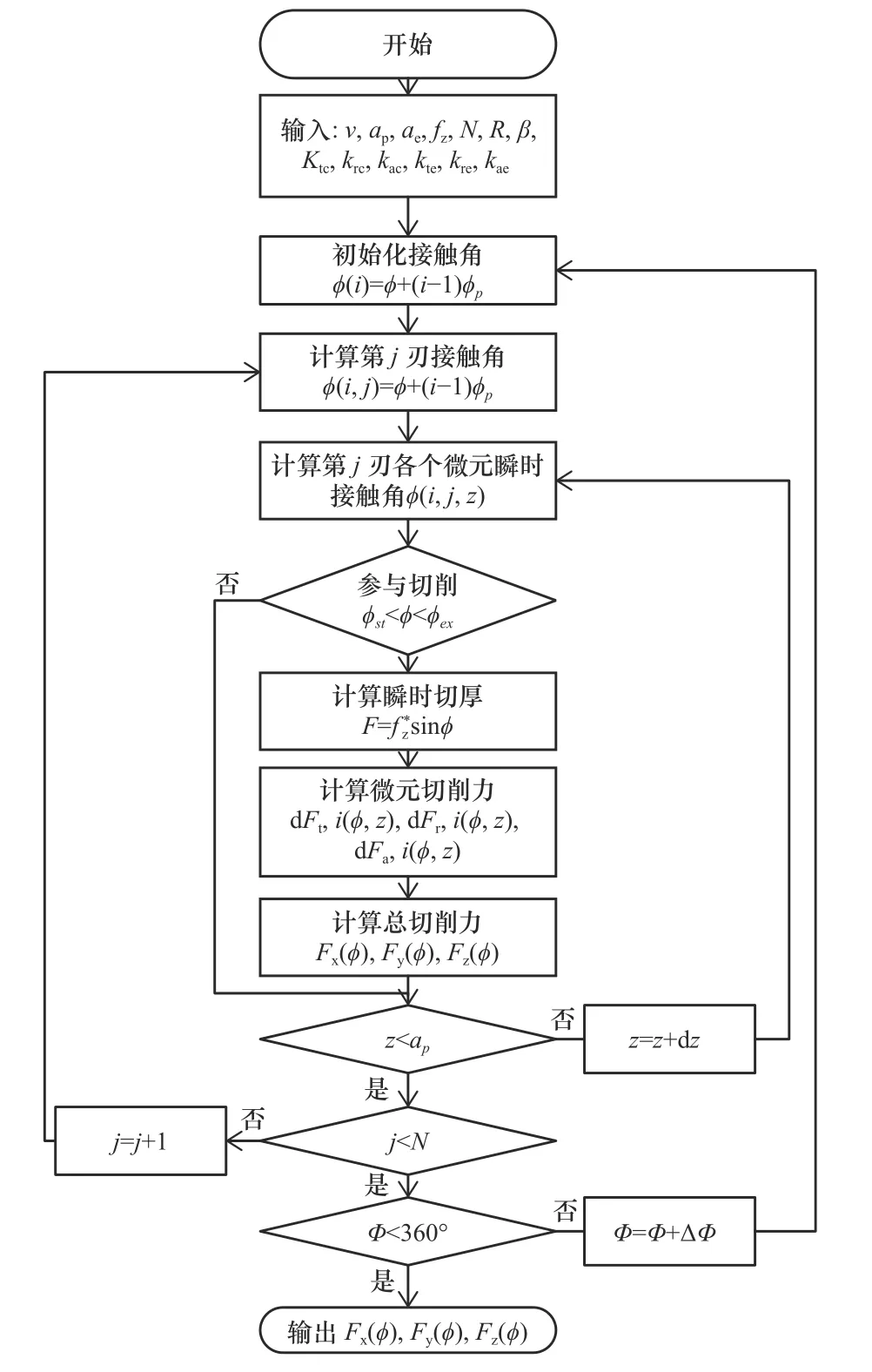
圖2 銑削力算法流程圖
3 鈦合金型面?zhèn)缺阢娤髟囼?yàn)
切削試驗(yàn)所選用的工件材料為鈦合金Ti-6A1-4V塊料,其屬于α+β雙相合金,主要化學(xué)成分含量百分比見表1,主要物理力學(xué)性能參數(shù)見表2。

表1 Ti-6A1-4V化學(xué)成分
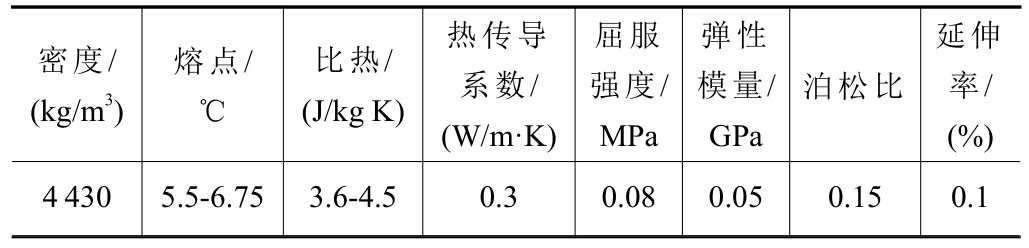
表2 Ti-6A1-4V物理及力學(xué)性能
本試驗(yàn)所使用的機(jī)床型號(hào)為DAEWOO ACE V500立銑床,刀具為實(shí)驗(yàn)室自主研制的整體硬質(zhì)合金立銑刀,其基本性能參數(shù)如表3所示,涂層材料為TiAlN復(fù)合涂層。加工方式為順銑,干切削。首先將鈦合金工件通過連接件與Kistler 9257B測(cè)力裝置固定并一同夾緊固定在銑床工作臺(tái)面上,所測(cè)得的切削力信號(hào)首先需要經(jīng)過5070A電荷放大器放大,再經(jīng)由5697A信號(hào)采集器后借助于電腦端安裝的DynoWare分析軟件記錄并保存數(shù)值用于實(shí)驗(yàn)數(shù)據(jù)分析。試驗(yàn)裝置及測(cè)力裝置見圖3。

圖3 試驗(yàn)機(jī)床及切削力測(cè)量裝置
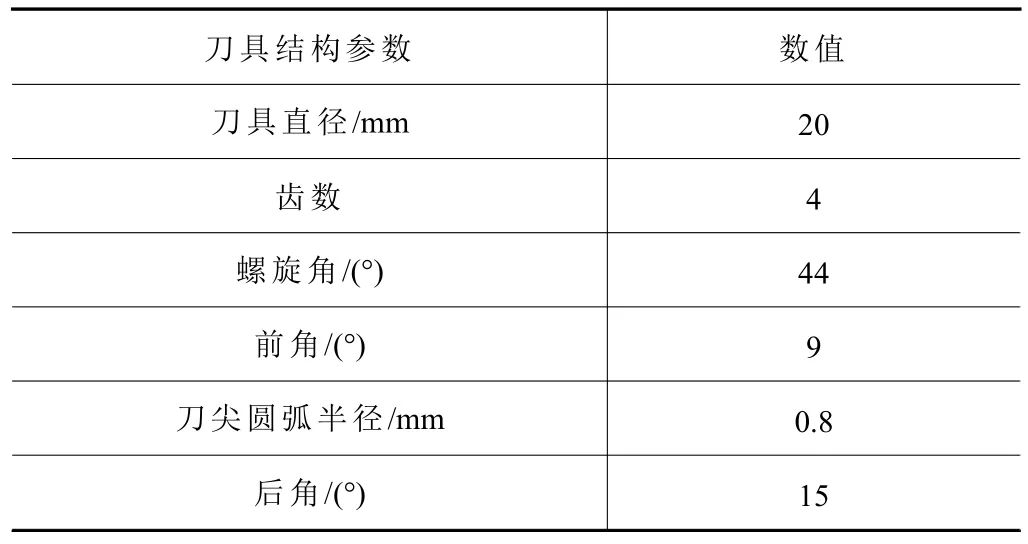
表3 刀具幾何參數(shù)[10]
每組試驗(yàn)的選取10個(gè)峰值切削力并取平均值用于計(jì)算微元切削力系數(shù),切削力辨識(shí)試驗(yàn)參數(shù)設(shè)置如表4,經(jīng)計(jì)算所得鈦合金工件材料切削力系數(shù)見表5。
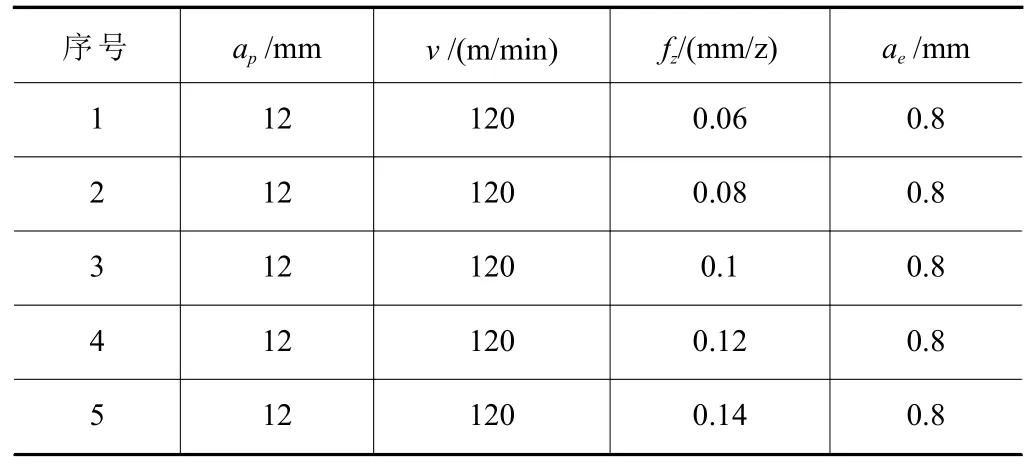
表4 切削力辨識(shí)試驗(yàn)參數(shù)
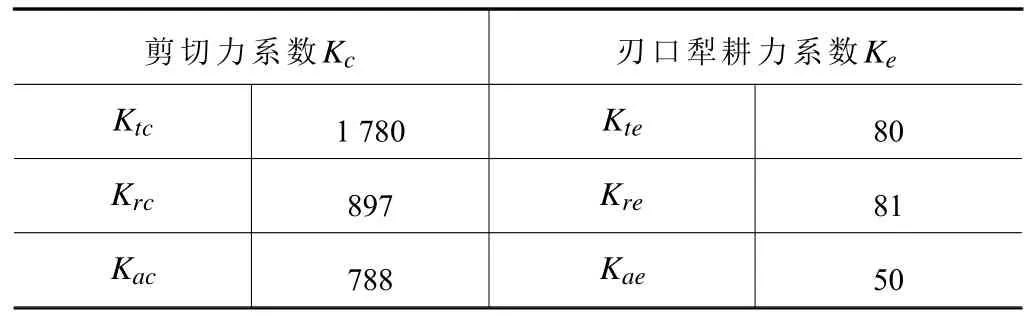
表5 立銑刀銑削力系數(shù)
4 銑削力模型驗(yàn)證與分析
隨機(jī)選擇4組銑削參數(shù)利用切削試驗(yàn)驗(yàn)證了主切削力多項(xiàng)式擬合的指數(shù)公式及仿真切削力預(yù)測(cè)的有效性。本驗(yàn)證試驗(yàn)中各切削參數(shù)設(shè)置見表6,主切削力試驗(yàn)值、仿真值及其各自對(duì)應(yīng)的相對(duì)誤差值見表7。
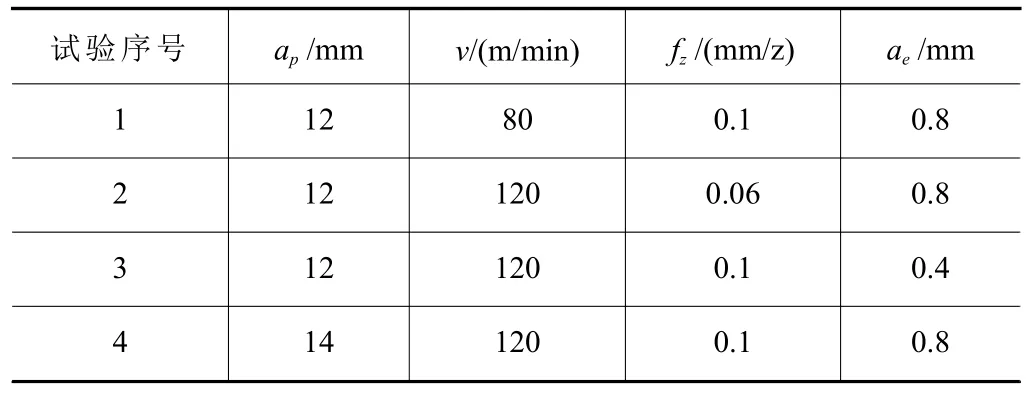
表6 驗(yàn)證試驗(yàn)切削參數(shù)
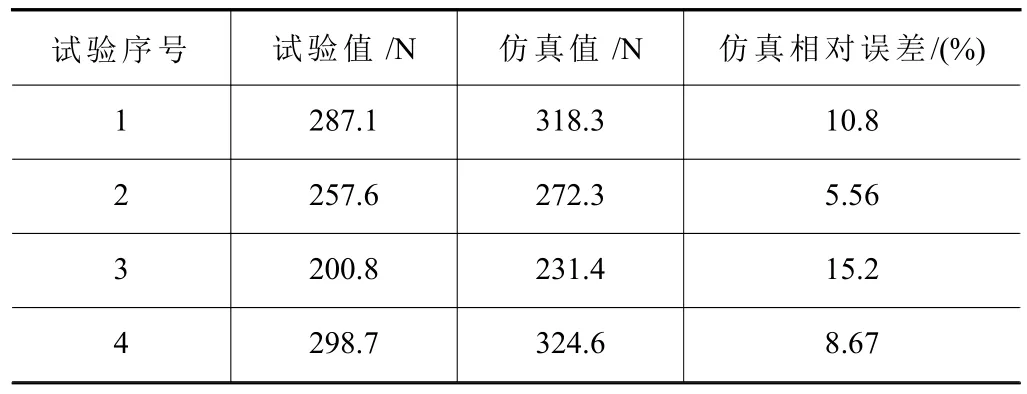
表7 兩種主切削力模型預(yù)測(cè)誤差
圖4為試驗(yàn)與仿真模型所得切削力對(duì)比圖,通過對(duì)4組鈦合金銑削試驗(yàn)的切削力實(shí)測(cè)值與仿真值對(duì)比,計(jì)算可得仿真模型誤差在5.56%~15.8%,可見所建立的銑削仿真模型具有較好的準(zhǔn)確度,并證明了本文中所提出的有關(guān)圓柱立銑刀切削力系數(shù)數(shù)值計(jì)算結(jié)果和主切削力預(yù)測(cè)模型的準(zhǔn)確性。
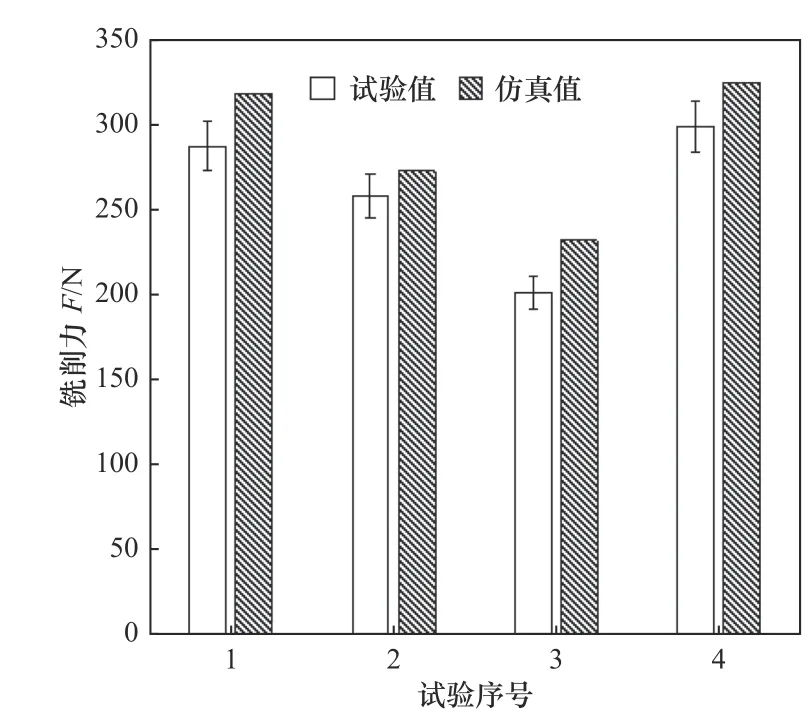
圖4 銑削力預(yù)測(cè)值對(duì)比
5 結(jié)語
通過對(duì)圓柱螺旋立銑刀幾何外形分析,將其沿銑刀切削刃劃分為若干個(gè)切削微元參與切削,進(jìn)而建立瞬時(shí)切削力模型,然后再通過空間坐標(biāo)變換和數(shù)值積分求和等基本操作建立圓柱螺旋立銑刀整體切削力數(shù)學(xué)計(jì)算公式,通過鈦合金側(cè)銑試驗(yàn)完成切削力系數(shù)辨識(shí),然后借助于Matlab程序完成了切削加工過程瞬態(tài)切削力仿真計(jì)算。
為驗(yàn)證模型的正確性,設(shè)計(jì)了鈦合金銑削驗(yàn)證試驗(yàn),仿真與試驗(yàn)結(jié)果的一致性證實(shí)了兩種模型的可靠性,經(jīng)驗(yàn)證可以得仿真模型誤差在5.56%~15.8%,可以較好地用于切削力的預(yù)測(cè)和參數(shù)變量?jī)?yōu)化,為鈦合金型面件側(cè)壁加工過程工藝參數(shù)制定和優(yōu)化奠定了理論基礎(chǔ)。

