基于MATLAB的滾柱活齒傳動滑動特性研究

王冉 王士軍 杜雅寧 齊娜 鄭蘇芮

（山東理工大學機械工程學院，山東 淄博 255000）

滾柱活齒傳動與行星齒輪傳動、諧波傳動和RV傳動相比具有很多優點，如結構緊湊、傳動比范圍廣、嚙合度高、承載能力大、傳動效率高和制造成本低[1]。隨著活齒傳動技術不斷發展，逐漸被廣泛應用于工業自動化、數控機床、衛星技術、工業機器人和數控機床等領域。因此，研究滾柱活齒傳動是一項具有巨大應用前景的研究。滑動率和滑滾比作為滾柱活齒傳動的重要參數，與傳動效率和活齒嚙合過程中的磨損密切相關，然而針對活齒傳動相關的滑動率和滑動比系統性研究非常少。因此，研究設計參數對滾柱活齒傳動的滑動率和滑滾比的影響變得越來越重要。

在目前的研究中，滾柱活齒傳動的研究主要討論中心輪齒形設計、傳動特性分析、嚙合剛度及承載性研究、嚙合建模與仿真。宜亞麗等提出一種計算對數修形復合滾柱活齒嚙合變形量的方法，分析了不同填充度對滾柱活齒嚙合剛度的影響規律，并通過有限元分析對嚙合處等效應力圖進行了對比分析[2]。王志剛等建立了滾柱活齒傳動平移-純扭轉耦合動力學模型，建立系統非線性動力學微分方程，通過改變參數偏心距和嚙合阻尼，分析了參數變化對系統非線性動態的影響[3]。韓曉娟等提出了一種新型可實現任意齒差數的活齒傳動，推導出中心輪齒廓方程，并對中心輪齒廓曲率、重合度和壓力角進行了影響因素分析[4]。Kato K提出了一種單球傳動活齒減速器，提高了能量效率，減少了傳動滑移，簡化了機構設計[5]。李勇進等用“等效機構法”推導了二齒差滾柱活齒傳動的嚙合曲線，提出了用矢量法求解激波凸輪中心輪實際齒廓線的方法，分析了不同參數修形方式與中心輪實際廓線曲率的關系[6]。陳楊等結合活齒嚙合原理，對滾柱活齒傳動的嚙合副進行研究，建立相關嚙合方程，采用可視化編程進行了滾柱活齒傳動的建模與仿真[7]。張帥等針對二齒差純滾動活齒內齒圈提出基于UG NX設計平臺的三維數字化設計與加工的方法，并進行了建模與仿真，提高了工作效率[8]。

基于滾柱活齒傳動的研究不少，但關于滾柱活齒的滑動特性很少有人研究。在本文中，通過結構特點和工作原理推導出滾柱活齒傳動的數學模型和運動學模型[9-10]，基于MATLAB軟件分析了設計參數激波器半徑、活齒半徑、傳動比和偏心距對滑動率和滑滾比的影響。

1 滾柱活齒傳動的運動學原理

滾柱活齒傳動主要有4個部分組成：激波器H、滾柱活齒G、中心輪K和活齒架M，如圖1所示。

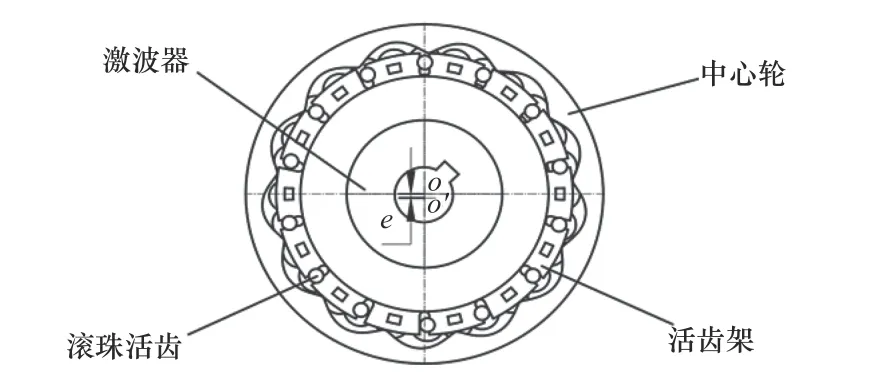
圖1 滾柱活齒傳動結構圖

在滾柱活齒傳動中激波器采用偏心凸輪，本文的研究對象中心輪是固定的，中心輪、活齒架和激波器是運動部件，利用機構轉換法，假設給活齒施加一個與其周向角速度大小相等方向相反的角速度，此時活齒在活齒槽中作上下往復運動，設激波器的角速度為ωH，中心輪的角速度為ωK，滾柱活齒的角速度為ωG，根據三者的運動關系可以計算出傳動比如式（1）所示。

本文的中心輪是固定的，激波器作為輸入帶動滾柱活齒轉動，在活齒架和中心輪的約束下，滾柱活齒驅動活齒架輸出角速度，其中ωK為0，偏心凸輪作為激波器通常為一齒差結構，計算傳動比如式（2）所示。

式中：ZK為中心輪齒數；ZG為活齒齒數；“+”表示同向傳動；“-”表示反向傳動。

滾柱活齒傳動的中心輪齒形設計對整個結構是十分重要的，通常需要根據結構的設計參數來確定，首先根據激波器和活齒的運動軌跡確定滾柱活齒的運動曲線方程，中心輪的齒廓曲線則為滾柱活齒的外包絡曲線。

如圖2a所示為滾柱活齒傳動結構簡圖，在OXY坐標系中已知中心輪固定，激波器作為輸入構件以某一角速度順時針勻速旋轉，滾柱活齒在激波器的作用下與中心輪嚙合，在中心輪的約束下推動活齒架以恒定角速度順時針旋轉。

設滾柱活齒中心曲線的徑向矢量OM=p，激波器半徑為Rd，激波器的偏心距為e，活齒的半徑為r。確定參數后可以得到中心輪理論齒廓線方程s-s方程為

式中：p為活齒中心的徑向矢量可以用方程表示為

式中：θH為激波器的轉角；θG為滾柱活齒的轉角。

如圖2b所示，中心輪實際齒廓線s′-s′為中心輪理論齒廓線的外等距線，α為y軸與s′-s′法線在嚙合點的夾角。中心輪的工作齒廓線可以表示為

通過包絡原理和如圖2所示結構分析得到中心輪理論齒廓線s-s和實際齒廓線s′-s′進而確定具體設計參數，如表1所示為本文研究的滾柱活齒傳動基本設計參數。

表1 滾柱活齒基本設計參數

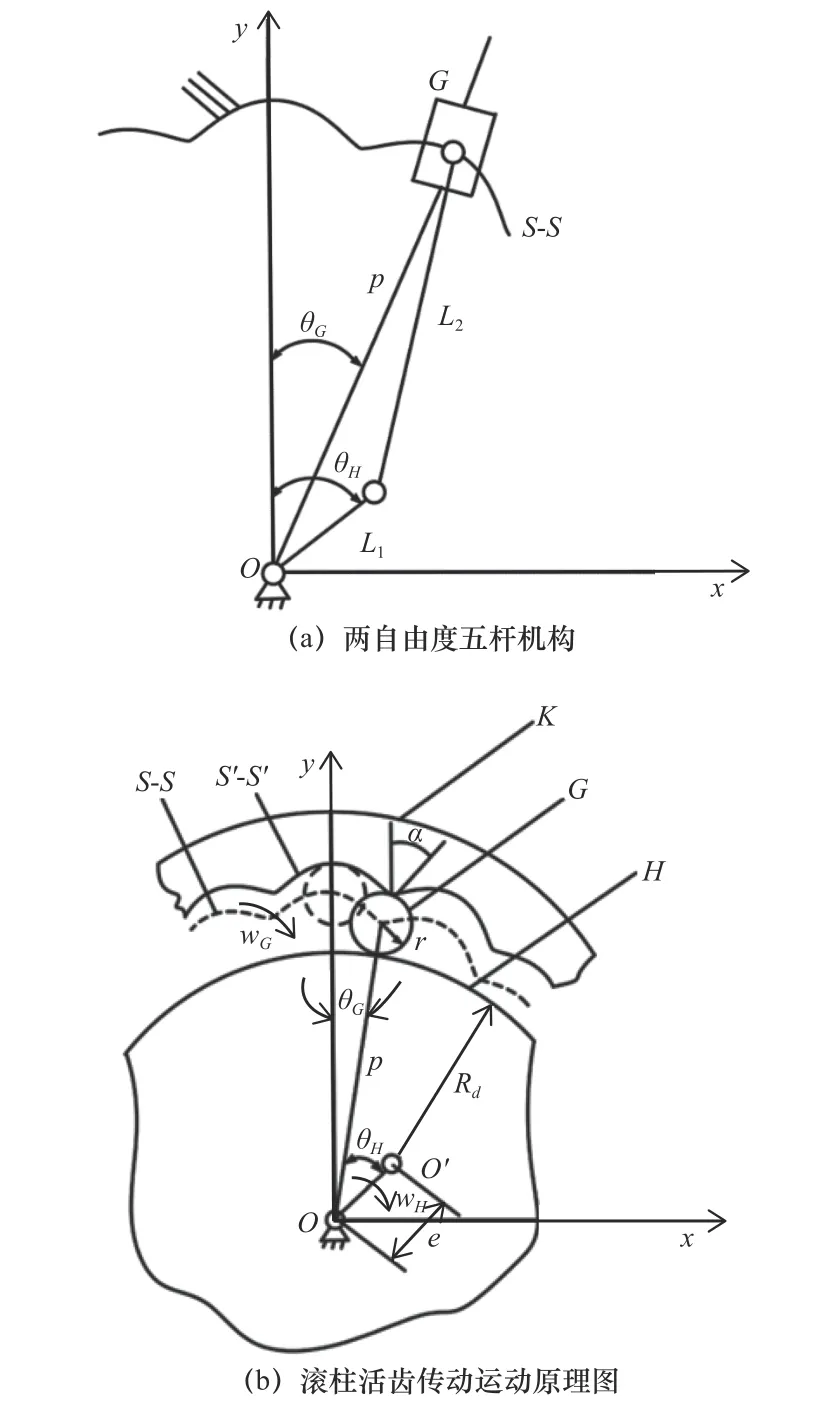
圖2 滾柱活齒傳動運動學模型

2 滾柱活齒傳動滑動模型的建立

滾柱活齒傳動由兩個高副和一個低副組成，高副在運動過程中因接觸點切向速度不同會產生相對滑動。滾柱活齒和中心輪之間的嚙合狀態是滾動與滑動并存的，滑動狀態的增加會產生較多的摩擦，造成運動構件的損耗、傳動不穩定和傳動效率低等問題。解決上述問題最好的方式就是提高滾柱活齒在工作過程中的滾動狀態。

目前國內外文獻中對滑動率的研究非常少，本文基于對一般曲線的滑動率和滑滾比的研究結合滾柱活齒的結構特點，將運動過程中滾柱活齒與中心輪的嚙合點相對滑動速度和切向速度的比值定義為滑動率。

式中：V1和V2分別為嚙合點1和2處的切向速度；S1和S2分別為嚙合點1和2的滑動率。

滑滾比可通過下式計算得到：

以滾柱活齒為研究對象，將滾柱活齒的速度進行分解：一是滾柱活齒在激波器驅動和中心輪齒形的約束下作圓周運動，此時的速度為VGg；二是滾柱活齒在活齒槽圍繞滾柱銷作自由轉動，此時的速度為VGt；三是滾柱活齒在活齒架內作上下往復運動，此時的速度為VGn，這3個方面的速度可用下式計算：

式中：VHt=VG/sinδi，VG=qωH，ωH=iωG，δi=π/2-ηi，μi=π-δi-γi，φi=2γi-ηi，

在滾柱活齒運動過程中有兩個方面會產生滑動，一方面為激波器與滾柱活齒之間，一方面中心輪與滾柱活齒之間。如圖3所示建立了滾柱活齒傳動滑動模型，假設激波器和滾柱活齒在嚙合點N2處為純滾動接觸，中心輪與滾柱活齒在嚙合點N1處運動規律不同又相互制約，因此中心輪與滾柱活齒之間一定會產生相對滑動。根據嚙合原理和一般曲線的滑動率公式確定計算公式。

圖3 滾柱活齒傳動滑動模型

中心輪滑動率S1計算公式為

滾柱活齒滑動率S2計算公式為

滾柱活齒傳動滑滾比S3計算公式為

式中：VKg=VGt。

3 參數對滑動率和滑滾比的影響分析

通過上述建立的滑動模型和方程，利用MATLAB軟件編寫程序，建立數值建模仿真[11]，分析滾柱活齒傳動設計參數激波器半徑Rd、滾柱活齒半徑r、激波器偏心距e和傳動比i對滑動率和滑滾比的影響規律。

在保證其他設計參數不變的情況下，研究激波器半徑Rd對滾柱活齒傳動滑動率和滑滾比的影響，將激波器半徑從55 mm增加到75 mm，每次增加5 mm，經過數值建模分析得到激波器半徑對滾柱活齒傳動滑動率和滑動比影響如圖4所示。

由圖4a可知，當活齒轉角θG從0逐漸增加到0.448 7 rad時，激波器轉動一圈，滾柱活齒完成從齒根到齒頂再次回到齒根的整個運動過程，中心輪滑動率S1先增大后減小，滑動率的變化率先增大后減小，在齒頂滑動率的變化率達到最小，在滾柱活齒和中心輪的嚙合點處，中心輪滑動率的變化率最大。當激波器半徑增加時，中心輪滑動率峰值增大，激波器半徑每增加5 mm，中心輪滑動率峰值增大約0.21%，滑動率變化趨勢越來越平緩。

由圖4b可知，隨著活齒轉角θG從0增加到0.448 7 rad，活齒滑動率S2先減小后增大，活齒滑動率變化率先增大后減小，在嚙合點處滑動率變化率最大，在齒頂處變化率最小。隨著激波器半徑每增加5 mm，活齒滑動率峰值減小約6.67%，滑動率變化趨勢越來越平緩。

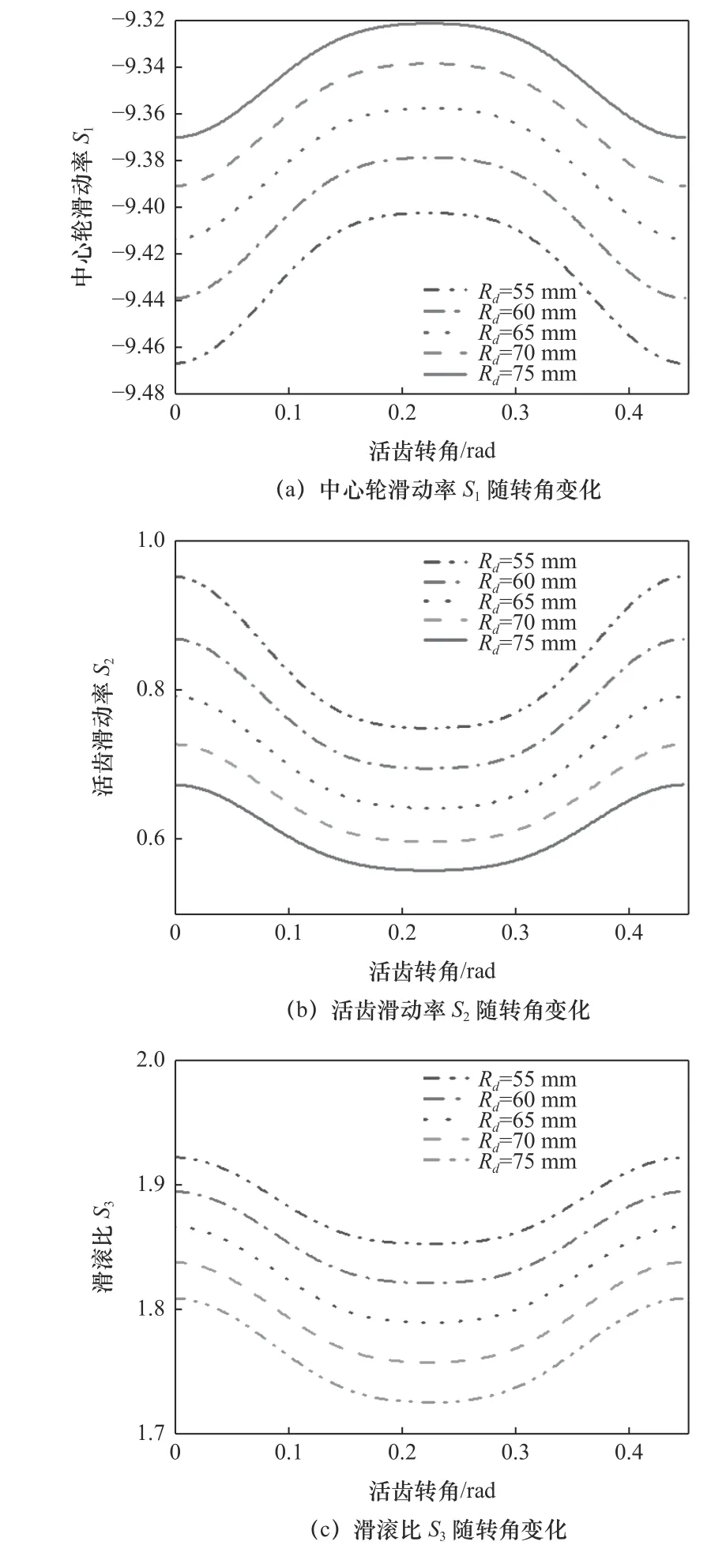
圖4 激波器半徑對滑動率和滑滾比的影響

由圖4c可知，隨著活齒轉角θG從0增加到0.448 7 rad，滑滾比S3先減小后增大，在嚙合點處滑滾比的變化率最大，在齒頂處變化率最小，滑滾比的峰值出現在中心輪的齒根處，激波器半徑每增加5 mm，滑滾比峰值減小約1.62%。

在保證其他參數不變時，研究滾柱活齒半徑r對滾柱活齒傳動的滑動率和滑滾比影響，將滾柱活齒半徑從4 mm增加到8 mm，每次增加1 mm，得到滾柱活齒半徑對滑動率和滑動比的影響如圖5所示。

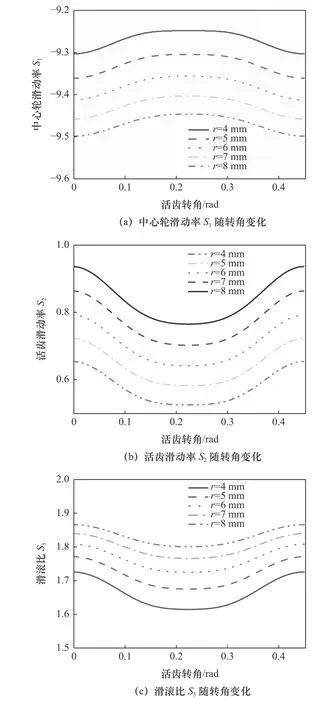
圖5 滾柱活齒半徑r對滑動率和滑動比的影響

由圖5a和5b可知，隨著活齒轉角θG從0到0.448 7 rad，中心輪滑動率S1先增大后減小，滑動率變化率較小。隨著滾柱活齒半徑的增大中心輪滑動率峰值減小，在齒頂處達到峰值，每增大1 mm，峰值減小約0.54%。活齒滑動率S2正好相反，隨著活齒轉角θG增加，活齒滑動率S2先減小后增大，滑動率變化率較大，隨著活齒半徑的增大，活齒滑動率峰值增大，每增大1 mm，峰值增大約10.3%。

由圖5c可知，隨著活齒轉角θG從0增加到0.448 7 rad，滑滾比S3先減小后增大，滑滾比變化率在嚙合點處最大，在齒頂處滑動率變化率最小。隨著滾柱活齒半徑的增大，滑滾比峰值增大，增大的速度越來越慢。

當保證其他參數不變時，研究偏心距e從2 mm增加到4 mm，每次增加0.5 mm對滾柱活齒傳動的滑動率和滑動比的影響，如圖6所示。

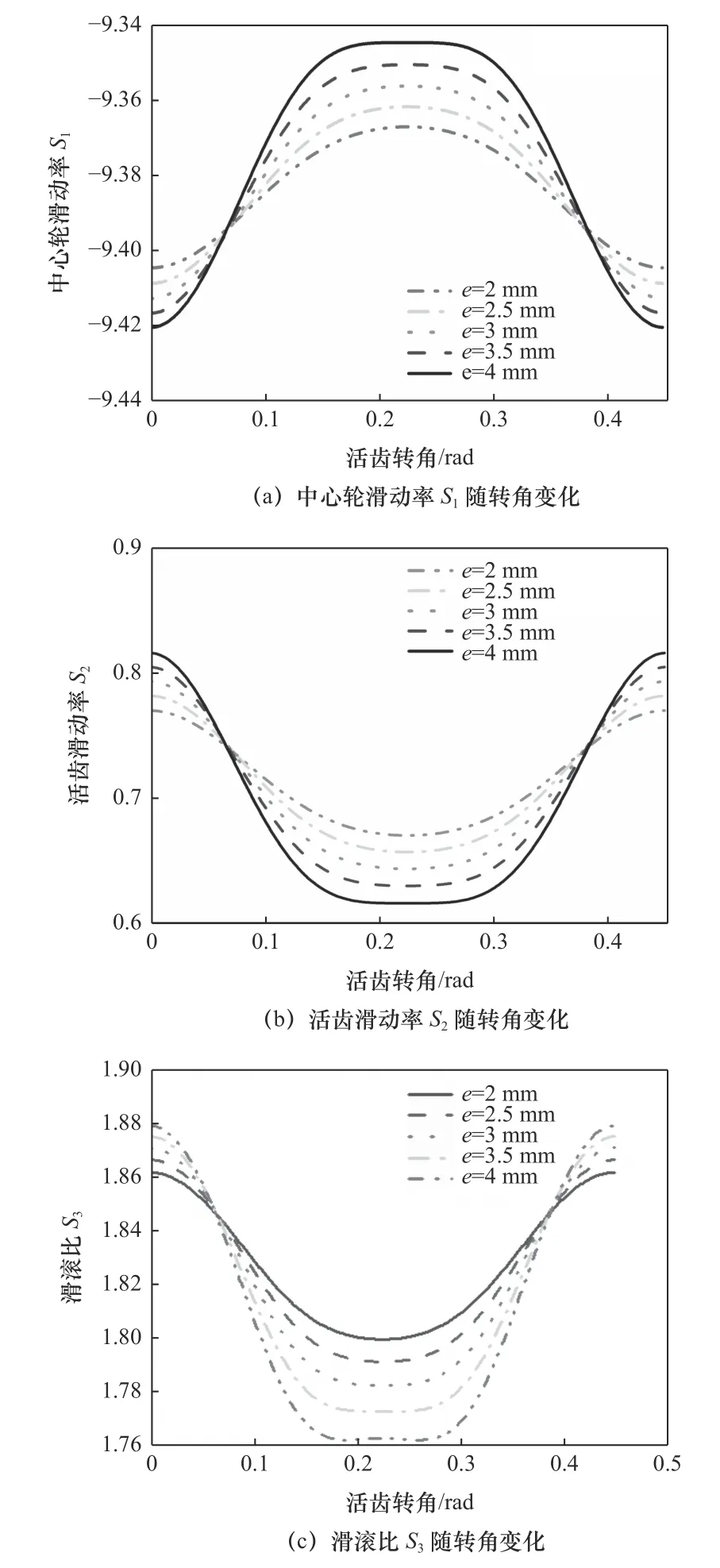
圖6 偏心距e對滑動率和滑滾比的影響

由圖6a和6b可知，隨著活齒轉角θG從0到0.448 7 rad，中心輪滑動率S1先增大后減小，滑動率變化率較小，活齒滑動率S2先減小后增大，滑動率變化率較大。隨著偏心距的增加，中心輪滑動率峰值增大，每增加0.5 mm，中心輪滑動率峰值增大約0.005，在齒頂處達到峰值。相反，隨著偏心距的增大，活齒滑動率減小，每增大0.5 mm，活齒滑動率峰值減小約0.011，在齒根處達到峰值。在拐點處，無論偏心距怎樣變化，中心輪滑動率和活齒滑動率都不改變，而且在拐點后滑動率的變化趨勢越來越大。

由圖6c可知，隨著活齒轉角θG從0增大到0.448 7 rad，滑滾比S3先減小后增大，在嚙合點處，無論偏心距變大還是變小，滑滾比S3都是保持不變的。隨著偏心距的增大，滑滾比S3的變化率越來越大，在齒根處滑滾比達到最大值，在齒頂處達到最小值。滑滾比的峰值隨著偏心距每增大0.5 mm，相應增大約0.004。

當保證其他參數不變時，研究傳動比i從12到16，每次增加1，對滾柱活齒傳動滑動率和滑動比的影響。因為傳動比不同會導致滾柱活齒從齒根到齒頂再到齒根的活齒公轉角范圍發生改變，表2為不同傳動比對應的滾柱活齒公轉角。

表2 滾柱活齒公轉角

由圖7a、b可知，隨著活齒轉角θG增大，在對應的滾柱活齒公轉角范圍內，中心輪滑動率S1先增大后減小，滑動率變化率較小，在齒頂處滑動率達到最大值；活齒滑動率S2先減小增大，滑動率變化率較大，在齒根處活齒滑動率達到最大值。隨著傳動比增加，滾柱活齒在一個工作行程中公轉角范圍減少，中心輪活齒滑動率減小，并且減小的趨勢變得緩慢；隨著傳動比增大，活齒滑動率增大，增大的速度保持恒定。

由圖7c可知，隨著活齒轉角θG增大，滑滾比S3先減小后增大，在齒根處滑滾比達到最大值，在齒頂處滑滾比達到最小值；滑滾比變化率在嚙合點處最大，在齒頂處最小。隨著傳動比的增大，滑滾比增大，滑滾比增大的速度變得越來越緩慢。

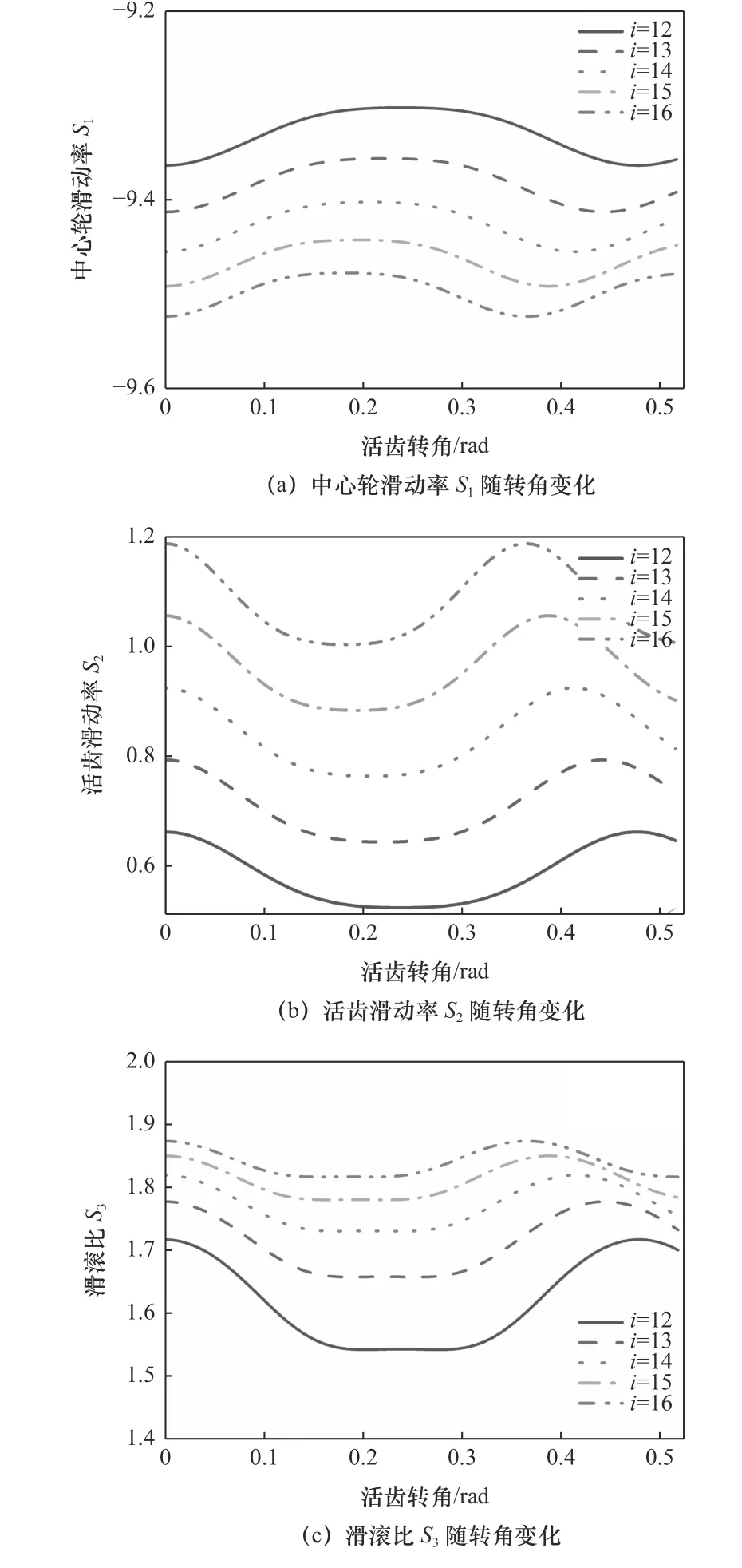
圖7 傳動比i對滑動率和滑滾比的影響

4 結語

本文基于滾柱活齒傳動的結構特點和工作原理，建立了滾柱活齒傳動的運動學模型，基于運動學原理，提出了滾柱活齒傳動滑動模型，利用數值分析建模的方法分析了設計參數的變化對滑動率和滑動比的影響。研究結果可以為設計滾柱活齒傳動結構參數提供依據，降低滑動率和滑滾比，減少傳動摩擦，提高傳動效率。

（1）中心輪滑動率S1和活齒滑動率S2的絕對值和滑滾比S3隨著活齒轉角θG增大先減小后增大，在嚙合點處，滑動率和滑滾比的變化率最大，在齒頂處變化率最小。

（2）隨著激波器半徑Rd和偏心距e增大，中心輪滑動率S1增大，活齒滑動率S2和滑動比S3減小；當滾柱活齒半徑r和傳動比i增大時，中心輪滑動率S1減小，活齒滑動率S2和滑滾比S3增大。

（3）滾柱活齒半徑r對活齒滑動率影響較大，隨著活齒半徑增大，每增大1 mm，活齒滑動率峰值增大約10.3%。偏心距e對滑動率和滑滾比變化率的影響較大，在嚙合點處無論偏心距怎樣變化，滑動率和滑滾比保持不變，并且過了嚙合點偏心距越大，滑動率和滑滾比的變化率越快。