基于RCMDE與極限學(xué)習(xí)機(jī)的滾動軸承故障診斷*
劉云斌 錢俊 潘曙明
(①金華市技師學(xué)院,浙江 金華 321017;②浙江大學(xué),浙江 杭州 310000)
旋轉(zhuǎn)機(jī)械被廣泛用于各種現(xiàn)代工業(yè)中,例如風(fēng)力發(fā)電機(jī)、航空發(fā)動機(jī)和水輪機(jī)等。作為其中的主要零件,滾動軸承十分重要。由于工作環(huán)境惡劣,滾動軸承很容易出現(xiàn)故障,滾動軸承的故障一般包括滾動體故障、內(nèi)圈故障和外圈故障等,因此開展關(guān)于滾動軸承的故障診斷技術(shù)的研究是必不可少的[1-3]。
由于滾動軸承信號具有非平穩(wěn)、非線性的特點(diǎn),并且滾動軸承故障類型較多,傳統(tǒng)故障診斷方法如基于時(shí)域、頻域的故障診斷方法難以有效地提取故障特征從而導(dǎo)致故障識別率較低[4-5]。
熵是熱力學(xué)中衡量系統(tǒng)穩(wěn)定性質(zhì)的一個(gè)參量,將其擴(kuò)展到信息學(xué)中就得到了信息熵理論。作為信息熵的其中一種,離散熵可以用來計(jì)算一段時(shí)間序列復(fù)雜度,其不需要對每個(gè)嵌入矢量的幅值進(jìn)行排序,所以計(jì)算速度快[6-8]。而多尺度粗粒化操作可以將熵?cái)U(kuò)展到多個(gè)時(shí)間尺度,可以提供多個(gè)尺度的觀察視角,所以RCMDE可以得到更多的故障信息,通過計(jì)算原始信號的RCMDE能夠獲得充足的故障特征,進(jìn)而能夠?qū)崿F(xiàn)故障的精確區(qū)分[9-11]。
機(jī)器學(xué)習(xí)的發(fā)展促使傳統(tǒng)故障診斷階段過渡到了智能診斷階段,而當(dāng)前的智能診斷技術(shù)往往依靠神經(jīng)網(wǎng)絡(luò)算法來實(shí)現(xiàn)。作為一種先進(jìn)的前饋神經(jīng)網(wǎng)絡(luò)算法,ELM具有計(jì)算速度快與泛化性好的優(yōu)點(diǎn),因此,其很快被引入到故障診斷領(lǐng)域并得到了廣泛應(yīng)用[12-13]。
本文將RCMDE應(yīng)用在故障特征的提取上,提出一種基于精細(xì)復(fù)合多尺度離散熵與極限學(xué)習(xí)機(jī)的軸承故障診斷方法。
1 離散熵與精細(xì)復(fù)合多尺度離散熵
1.1 離散熵(DE)
離散熵可以用來表示一段時(shí)間序列的不規(guī)則程度。給定一段長度為N的時(shí)間序列x={x1,x2,x3,···,xN},計(jì)算它的離差熵過程如下:
(1)首先,需要將x線性映射到一個(gè)1到c的正整數(shù)分類序列。考慮到信號的不規(guī)則性,即在一段信號序列中可能會出現(xiàn)一個(gè)信號的最大值或最小值比信號的均值大很多或者小很多的情況,從而導(dǎo)致信號大部分集中在這個(gè)序列的一個(gè)子集中。因此,通過正態(tài)累積函數(shù)(NCDF)將x映射至一個(gè)0~1的序 列y={y1,y2,y3,···,yN},正態(tài)累積函數(shù)的表達(dá)式如下。
其中:σ為所求序列的標(biāo)準(zhǔn)差,μ為所求序列的均值。
(2)得到序列y后,將其線性映射至z,公式如下。
其中:a表示為第a個(gè)等級,表示分類序列的第j個(gè)元素,round(·)表示四舍五入操作。
其中:i=1,2,3,···,N-(m-1)d,m是嵌入維度,d是時(shí)間延遲。
因此一共有am種不同的離散圖。對于每一個(gè)可能存在離散圖,其相對頻率的表達(dá)式為
(5)根據(jù)熵的定義,可求得離散熵,表達(dá)式如下。
(6)最后將由離散熵標(biāo)準(zhǔn)化公式得到標(biāo)準(zhǔn)離散熵。
1.2 精細(xì)復(fù)合多尺度離散熵
故障軸承的振動信號的非平穩(wěn)性和不規(guī)律性往往是很強(qiáng)的,RCMDE可以很好地解決這個(gè)問題,并且在處理非平穩(wěn)信號時(shí)具有很強(qiáng)的特征提取能力。它的計(jì)算過程如下:
(1)首先進(jìn)行多尺度粗粒化處理,粗粒化處理過程是一種簡單的求平均值的操作,假設(shè)時(shí)間序列為x={x1,x2,x3,···,xN},其多尺度粗粒化操作公式為
其中:τ是尺度因子,是原始時(shí)間序列的第k個(gè)粗粒化粒子。
(2)對于每個(gè)尺度,RCMDE的計(jì)算如下。
RCMDE的流程如圖1所示。
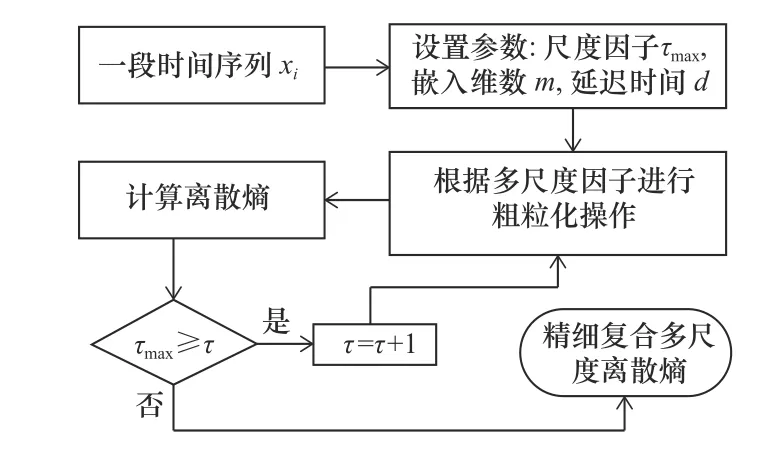
圖1 計(jì)算RCMDE流程
2 極限學(xué)習(xí)機(jī)
給一個(gè)元素個(gè)數(shù)為N的樣本數(shù)據(jù)集 (xi,ti),其中xi=[xi1,xi2,xi3,···,xin]T為輸入數(shù)據(jù),n為輸入層維度,ti=[t1,t2,t3,···,tim]T為樣本輸出值,m是輸出層維度。一個(gè)隱含層節(jié)點(diǎn)數(shù)為L的單層前向傳播神經(jīng)網(wǎng)絡(luò)的輸出公式為
其中:h(bixi+ci) 為激活函數(shù),i是指第i個(gè)隱含層節(jié)點(diǎn),bi為該隱含層節(jié)點(diǎn)和輸入層節(jié)點(diǎn)之間的權(quán)重,ci為該節(jié)點(diǎn)的偏置,βi為該隱含層節(jié)點(diǎn)和輸出層節(jié)點(diǎn)之間的權(quán)重,yi為輸出。
公式(11)可以簡化為Hβ=T。H為隱含層輸出層矩陣,T為期望輸出。使用最小二乘法確定極限學(xué)習(xí)機(jī)的輸出權(quán)重向量 βi,則
其中:H+為H的廣義逆矩陣,I為單位矩陣。為提高算法的穩(wěn)定性和泛化能力,在矩陣HHT中加入矩陣是懲罰因子。
3 實(shí)驗(yàn)分析
實(shí)驗(yàn)采用凱斯西儲大學(xué)的軸承數(shù)據(jù)對提出方法進(jìn)行了驗(yàn)證。測試軸承為6205-2RS JEM SKF,在旋轉(zhuǎn)速度為1 797 r/min和采樣頻率為12 000 Hz的條件下,從驅(qū)動端獲取軸承信號。本文將軸承振動信號分為4類,即無故障的滾動軸承和具有滾動體故障的滾動軸承,具有外圈故障的滾動軸承和具有內(nèi)圈故障的滾動軸承。3種故障軸承都分別有3種故障尺寸,分別為0.007 英寸,和它的2倍與3倍大小(1 英寸=25.4 mm)。將每種軸承振動信號的2 048個(gè)點(diǎn)劃分為一個(gè)樣本,其中正常軸承有50個(gè)樣本,3種故障軸承各有150個(gè)樣本,共有500個(gè)樣本。表1中給出了樣本的詳細(xì)描述。各狀態(tài)信號的時(shí)域圖如圖2所示。
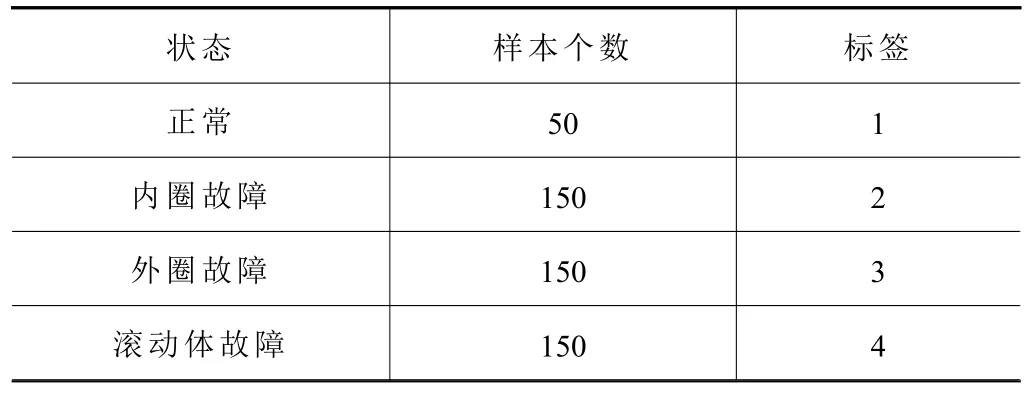
表1 樣本劃分
本文選擇的精細(xì)復(fù)合多尺度離散熵的參數(shù)為最大尺度因子τ=20,嵌入維數(shù)m=2,延遲時(shí)間d=1。圖2中信號計(jì)算RCMDE之后的結(jié)果如圖3所示。可以看出,在整體上來說正常軸承信號的RCMDE值比其他狀態(tài)軸承信號的RCMDE都大(第一個(gè)尺度除外),外圈故障軸承信號的RCMDE最小(第一個(gè)尺度除外),此外,可以看出各種狀態(tài)的軸承信號的RCMDE值差異較大,很容易區(qū)分開來,這樣對最后的分類十分有利。在對軸承的振動信號進(jìn)行精細(xì)復(fù)合多尺度離散熵計(jì)算之后可以得到500×20的特征集。為了適應(yīng)于工程實(shí)踐要求,隨機(jī)選取總體樣本的20%作為訓(xùn)練樣本用來訓(xùn)練核極限學(xué)習(xí)機(jī)的模型,剩余80%的樣本作為測試樣本。

圖2 各狀態(tài)軸承信號時(shí)域圖
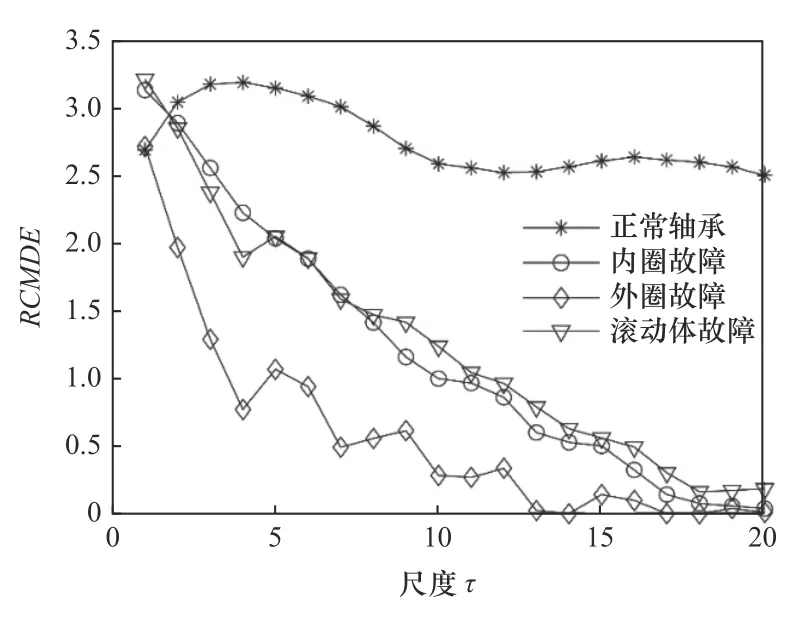
圖3 各狀態(tài)信號計(jì)算RCMDE結(jié)果
為了研究尺度因子對分類精度的影響,將尺度因子分別設(shè)置為τ=1,τ=5,τ=10,τ=20,嵌入維度與延遲時(shí)間保持不變,即取第1個(gè)尺度、前5個(gè)尺度、前10個(gè)尺度與前20個(gè)尺度的RCMDE值,之后利用極限學(xué)習(xí)機(jī)進(jìn)行了分類,分類結(jié)果表2所示。從表2中可以看出從τ=1 與τ=5、τ=10、τ=20之間分類精度差別很大,它們之間最大的區(qū)別在于τ=1時(shí),RCMDE就退化成DE。
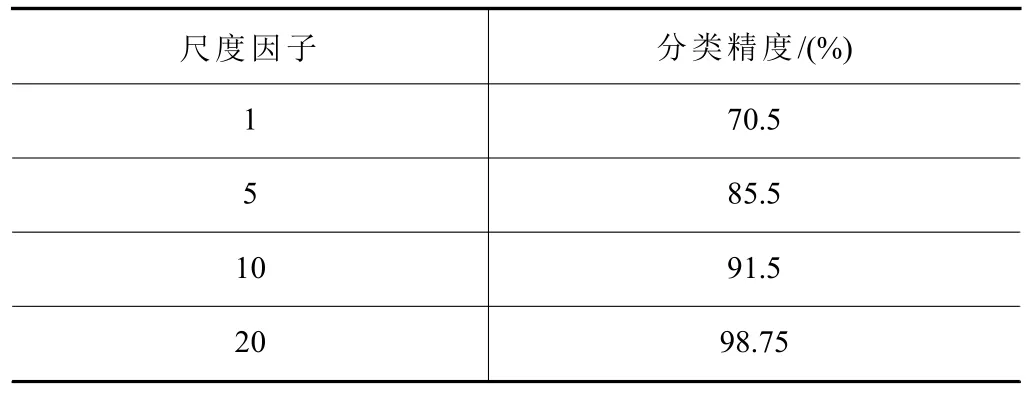
表2 分類結(jié)果
本文實(shí)驗(yàn)是在隨機(jī)選取樣本的條件下進(jìn)行的,為了減小偶然性影響,共進(jìn)行了10次實(shí)驗(yàn)。并通過改變極限學(xué)習(xí)機(jī)的輸入與提出的方法進(jìn)行了對比。用來對比的輸入通過計(jì)算軸承信號的多尺度排列熵獲得。10次實(shí)驗(yàn)的結(jié)果如圖4所示。從圖4可以看出,提出的故障診斷方法的分類效果總是比MPEELM的分類效果好,提出的方法的最大分類精度達(dá)到了99.75%,最小分類精度為97.25%。而MPEELM的最大分類精度為97.25%,最小分類精度為96%。并且通過計(jì)算可以得出在這10次實(shí)驗(yàn)中,提出的方法的分類精度的平均值達(dá)到了98.725%,MPE-ELM的分類精度的平均值為96.85%。
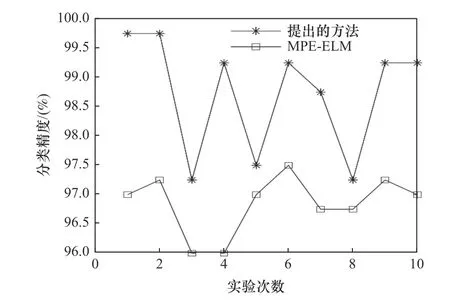
圖4 實(shí)驗(yàn)結(jié)果
4 結(jié)語
本文提出了一種基于RCMDE和ELM的軸承故障診斷方法。利用精細(xì)復(fù)合多尺度離散熵提取軸承信號的故障特征,然后輸入到核極限學(xué)習(xí)機(jī)進(jìn)行分類。將這樣的實(shí)驗(yàn)重復(fù)10次,在最終的分類結(jié)果中最大分類精度達(dá)到了99.75%,最小分類精度達(dá)到了97.25%,分類精度的平均值達(dá)到了98.725%,并通過與MPE-ELM的對比證明了本文提出的軸承故障診斷方法的有效性。

