考慮電動汽車集群及碳捕集廠的經濟調度研究

周鵬華，賴偉鵬，張昌鴻，陳璟華

（廣東工業大學 自動化學院，廣州 510006）

2020年9 月，我國提出“雙碳”目標，力爭于2030年前CO2排放達到峰值，并在2060年前實現碳中和[1]。近年來，電動汽車因其在節能減排方面的巨大潛力得到快速發展[2-3]，且隨著V2G技術與充電基礎設施的不斷完善，電動汽車能夠實現充電和放電，被視為一種具備儲能特性的設備，通過集中管理實現與新能源的協調互補運行。文獻[4]提出電動汽車通過聚合商參與電網運行，聚合商滿足電動汽車的充電要求，參與電網調度。文獻[5]將電動汽車集中控制器作為儲能設備并與分布式新能源結合，構建含電動汽車及可再生能源的新型安全約束經濟調度模型。

碳捕集技術被認為是減少化石能源發電過程碳排放的關鍵技術[6-7]。文獻[8]構建含碳捕集電廠-風電的魯棒經濟調度模型，并用算例說明碳捕集電廠能有效減少風電預測誤差對系統造成的影響。文獻[9]對碳捕集電廠靈活運行方式進行了詳細論述，并探討碳捕集電廠靈活運行方式對風電波動的抑制情況。文獻[10-11]構建碳捕集-電轉氣框架，將捕集的CO2作為原料提供給電轉氣。上述文獻對碳捕集電廠參與電網調度進行了研究，但未考慮大規模電動汽車并網對電網運行帶來的影響，在電動汽車協同調度作用下對系統可再生能源消納及電力低碳化的影響有待進一步研究。

針對上述情況，本文提出大規模電動汽車及碳捕集電廠協同調度促進電力系統低碳化及風電消納的優化調度模型。一方面電動汽車充電特性與風電反調峰特性互補，使電力系統的風電消納能力得到提升。另一方面傳統火電機組加裝碳捕集系統能有效減少機組運行產生的碳排放，有效提升電力系統穩定性。在上述基礎上，考慮風電及電動汽車的不確定性，提出考慮大規模電動汽車及碳捕集電廠的含風電電力系統模糊機會約束低碳經濟調度模型。算例仿真驗證了模型在提升風電消納及實現系統低碳化方面的有效性。

1 電動汽車集群建模

1.1 電動汽車充電負荷預測

大規模電動汽車行駛里程及出行規律會呈現一定概率分布，此時充電負荷預測值與實際數值吻合度較高[12]，在確定概率密度函數后，本文采用拉丁超立方抽樣對大規模電動汽車充電行為進行日前需求預測。目前電動汽車充電負荷預測數據大多數使用2009年美國家庭交通調查統計數據，但不同國家由于生活環境與習俗的不同，出行規律也會存在部分差異，因此本文將采用文獻[12]的北京私家車出行數據進行分析，更能體現我國私家車出行特性。車主出行分類大致分為工作日出行、雙休日出行及節假日出行，對私家車而言，需要足夠的充電時間來保證電動汽車離網時的電量，因此并網充電大概率選擇一天中最后一次結束出行的時刻，而車主首次出行會停止電動汽車充電行為，因此推斷電動汽車首次出行數據為私家車離網時間。采用Matlab擬合工具箱，選用高斯分布模型對電動汽車行駛里程、離并網時間進行擬合。

1.2 電動汽車分群處理

隨著電動汽車規模不斷擴大，以電動汽車個體為調度對象勢必會導致維數災，而且電動汽車個體存在不確定性，對單臺電動汽車進行調度較為困難。因此，本文采用集群調度方式，將電動汽車個體按一定劃分策略進行分群處理，電動汽車以集群形式參與優化調度。

1.2.1 基于充電時間裕度的集群劃分

電動汽車并網充電的首要目標是使電動汽車電量達到自身期望值，電動汽車充電時間隨并網初始電量及充電功率不同而不同，部分電動汽車由于初始電量較低，需要足夠的充電時間，該類電動汽車就不便參與到電動汽車調度過程中來。基于上述劃分策略，本文將電動汽車集群劃分為常規集群Sdc1與可調度集群Sdc2，并通過充電時間裕度tk來評判，具體公式如下

式中：tk為充電時間裕度；tl為電動汽車離網時間；tc為電動汽車并網時間。

通過充電時間裕度來判斷電動汽車是否參與集群調度，tk>0說明電動汽車充滿電所需時間小于離并網時間差，代表電動汽車有多余時間參與充放電過程，考慮到tk略大于0的電動汽車可調度靈活時間較為有限，故將該類電動汽車列入常規集群中，選取tk>2的電動汽車作為優化調度對象。

1.2.2 基于并離網時間的集群劃分

在對電動汽車能否參與集群調度進行劃分后，常規集群Sdc1可作為運行調度集群電動汽車劃為統一集群，即將所有并網時間為ti、并網時間為tj的電動汽車列入離并網時間負荷直接并入電網，而可調度集群Sdc2需要計算不同時刻的充電功率與放電功率。為便于調度管理，本文采用離并網時間作為劃分指標，以24 h為標準，將電動汽車個體并網時間往前取整、離網時間往后取整時，將擁有相同離并網整時的可集群Sij中。

1.3 電動汽車集群調度模型

電動汽車分群后，各集群運行存在如下約束

式中：Ps，t，c為集群s在時刻t的充電功率；Ps，t，d為離并網時間集群s在時刻t的放電功率；ηc、ηd分別為電動汽車充電功率及放電功率；us，t，c為集群s在時刻t的充電狀態，當us，t，c=1時表示集群s處于充電狀態，us，t，c=0表示集群s處于停運狀態。us，t，d表示集群s在時刻t的放電狀態；Hs為集群充電能量需求；Ms為集群s中電動汽車數量；Ssoc，end，s，m為集群s第m輛電動汽車的離網荷電狀態；Ssoc，start，s，m集群s第m輛電動汽車的并網荷電狀態；cs，m為集群s第m輛電動汽車的電池容量；Pc，max、Pd，max為電動汽車的充電功率上限與放電功率上限；ts，in、ts，out分別為集群s統一并網時間及離網時間；Ds為集群放電能量極限；Ssoc，down，s，m為集群s第m輛電動汽車的最低荷電狀態。

上述公式（2）中，式一為充電能量需求約束，代表調度周期結束時電動汽車集群充電總能量滿足集群充電能量需求；式二為集群充電能量需求具體公式，該公式代表集群充電能量需求為集群中所有電動汽車荷電狀態達到期望值所需充電能量；式三表示各集群充放電功率需要在集群充放電功率上限之下，由于并離網時間的集群劃分采用整時劃分策略，個體充放電會存在整個最前和最后時間段未完全充放電，對集群充放電功率上限造成影響。因此最前和最后時間段的集群充放電功率上限為個體充放電功率乘以充電時間在該時間段的占比；式四為充電時間約束，代表電動汽車集群只有在電動汽車并網到離網這段時間內進行充放電；式五為電池充放電最大值約束，該公式表示集群在調度周期中不應出現充放電累積和超過總充電需求的過度充電情況及荷電狀態低于一定下限導致電動汽車電池壽命損耗的過度放電情況；式六為集群放電能量極限公式。

2 考慮電動汽車集群及碳捕集電廠的含風電電力系統模糊機會約束經濟調度模型

本文以系統綜合運行成本最小為目標函數，含電動汽車集群、碳捕集電廠、風電及電網運行約束，同時考慮風電及電動汽車的不確定性，引用模糊參數來表示風電功率及電動汽車充電需求的預測值，構建考慮電動汽車集群及碳捕集電廠的含風電電力系統模糊機會約束低碳經濟調度模型。

2.1 目標函數

基于低碳目標及提升風電消納能力，本文以火電機組運行成本及補償電動汽車參與V2G服務成本、風電棄電成本、碳交易成本及碳捕集設備折舊成本為目標函數，具體公式為

式中:TCp為火電機組運行總費用；TCc為電動汽車V2G服務成本；TCw為風電棄風懲罰成本；TCT為碳捕集設備折舊成本。

式中:Pi，t為機組i在t時段的出力；Fi（Pi，t）為機組i在t時段的耗量特性函數；ui，t為機組i在t時段的狀態；SUi表示機組i的啟動費用。

式中:ai、bi、ci為機組i的耗量特性系數。

式中:Sc為離并網時間集群數；ν為V2G服務支付的單位補償成本。

式中:r為單位棄風懲罰成本；Pfw，t為時刻t風力發電機組預測出力；Pw，t為t時刻風力發電機組上網功率。

式中:m為碳交易價格；Eq為機組全天的碳排放量；α為火電機組碳配額系數。

式中：Cz為除儲液罐外的碳捕集設備價格；ξ為凈殘值率；TN為除儲液罐外的碳捕集設備折舊年限；PY為單位體積儲液罐價格；BY為儲液罐體積；Tz為儲液罐折舊年限。

2.2 約束條件

2.2.1 功率平衡約束

式中：Pload，t為t時段的負荷需求，其中包含常規集群電動汽車充電負荷及電 網原始負荷；Pg，j，t為第g個碳捕集機組凈輸出功率；ug，t為碳捕集機組g在t時段的狀態。

2.2.2備用約束

式中：μ1、μ2、μ3分別為考慮電動汽車及風電不確定性的備用容量系數；Pg，max、Pg，min分別為碳捕集機組g的最大與最小凈輸出功率。

2.2.3 電動汽車集群運行約束

電動汽車集群運行約束需要充電能量需求約束、集群充放電功率上限約束、充電時間約束、電池充放電最大值約束，以上約束與公式（2）一致，此處不再贅述。

2.2.4 碳捕集約束

1）碳捕集能耗約束。碳捕集系統捕集CO2需要消耗能量，該類能耗屬于系統的運行能耗，與捕集CO2量相關。此外碳捕集系統本身存在的能量損失及準備運行所需能耗被稱為系統的維持能耗二者共同構成了系統的捕集能耗，具體如下所示

式中：Pg，j，t為碳捕集機組g在t時刻的凈輸出功率；Pg，t為碳捕集機組g在t時刻的總輸出功率；Pg，c，t為碳捕集機組g在t時刻的運行能耗；Pg，d，t為碳捕集機組g在t時刻的維持能耗；Eg，ico2，t為再生塔及壓縮機處理的CO2量；λo為碳捕集系統捕集單位CO2所需能耗。

2）CO2捕集約束。碳捕集電廠運行方式主要包含煙氣分流運行方式（富液分流運行方式）、儲液式運行方式及二者結合的綜合靈活運行方式，不同運行方式具有不同的能流特性及具體工作原理見文獻[12]，其中綜合靈活運行方式具有更大的調峰深度及更廣的功率調節范圍，具體公式如下

式中：Eg，ico2，t為再生塔及壓縮機處理的CO2量；Eg，gco2，t為儲液罐在t時刻提供的CO2量；ρo為煙氣旁路t時刻的煙氣分流比；Eg，cco2，t為碳捕集機組CO2凈排放量；Eg，bco2，t碳捕集機組CO2實際總排放量；βo為碳捕集效率；θk為機組碳排放強度。

3）碳捕集機組運行約束。

公式（14）中，式一為煙氣分流比約束，ρo為1代表此時煙氣全部進入碳捕集設備；式二為CO2處理量的上下限約束，代表碳捕集系統所能處理的CO2量存在限制，其中V為碳捕集的最大運行狀態，Pg，max為碳捕集機組g的最大輸出功率；式三為儲液罐中可存放的CO2量約束，左約束代表儲液罐最大可存儲的CO2量，右約束代表儲液罐最大可放出的CO2量；式四中Vg，s，t為儲液罐釋放CO2所需溶液的體積，MMEA為乙醇胺的摩爾質量，Mco2為CO2的摩爾質量，θm為再生塔所能解析量，μR為溶液濃度，σR為溶液密度；式五及式六為富液罐與貧液罐的體積變化約束，其中Vg，cf，t、Vg，cp，t分別為t時刻富液罐及貧液罐的體積；式七及式八為富液罐與貧液罐的體積約束，其中Vg，cr為儲液罐最大體積；式九、式十為儲液罐始末容量約束；其中Vg，cf，0、Vg，cp，0為機組初始富液罐與貧液罐容量體積，Vg，cf，24、Vg，cp，24為24點富液罐與貧液罐容量體積。

2.2.5 直流潮流安全約束

式中：Pij，max為第i節點與第j節點之間傳輸的最大功率；Pij，t第i節點與第j節點在t時刻傳輸功率。

2.2.6 風電機組出力上下限約束

2.2.7 火電機組約束

1）火電機組出力約束。

式中：Pi，min、Pi，max分別為機組i的出力最小值與最大值。

2）火電機組最小啟停時間約束。

式中：Toni，t-1、Toffi，t-1為機組i在t-1時刻連續運行時間及連續停運時間；MUT、MDTi分別為機組最小連續開機和停機時間。

3）火電機組爬坡約束。

式中：URi、DRi為機組i的最大爬坡速率與最大下降速率。

2.3 不確定性處理

目前風電與電動汽車充電需求的功率預測已經取得許多成果，然而預測過程并不能考慮現實生活中存在的所有因素，因此預測結果與實際結果會存在一定的偏差。而隨著風電并網容量增加及大規模電動汽車參與優化調度，預測誤差會被不斷擴大直到無法被忽略，故本文引用模糊參數來表示風電及電動汽車具有的不確定性，采用三角隸屬函數描述各不確定量

式中：為模糊參數，Ms，1，Ms，2，Ms，3為對應隸屬度參數，其他參數定義同理。

引入模糊參數后，原公式（2）中的式一、三、五及公式（15）轉變為模糊機會約束

其中：Cr{·}為該類事件的可信性；θ為系統的置信水平，模糊機會約束方程可按文獻[12]方法轉化為清晰等價類，然后用傳統方法進行求解，具體過程不再贅述。

3 算例分析

3.1 算例系統概述

本文采用文獻[12]中的IEEE39系統進行算例分析，系統包含10臺常規火電機組及1個300 MW、2個250 MW風電場，選擇將機組1與2改造為碳捕集機組。假設機組碳排放配額為0.7，電動汽車的電池為統一型號，充放電最大功率為6 kW，充放電效率為95%，離網荷電狀態為0.95，最低荷電狀態為0.2，百公里耗電量為16.3 kW·h/100 km，電池容量為72.19 kW·h。采用拉丁超立方抽樣抽取50 000輛可調度集群電動汽車，并按分群策略進行劃分。本文基于MATLAB 2018a及CPLEX12.5對模型進行優化求解。

本文設置4種運行場景以考查不同電動汽車并網及碳捕集電廠不同運行方式下的調度情況。4種運行場景具體如下。

1）常規火電機組及電動汽車無序充電下的經濟調度；

2）常規火電機組及電動汽車有序充放電下的經濟調度；

3）考慮分流式碳捕集電廠及電動汽車有序充放電下的經濟調度；

4）考慮綜合靈活運行碳捕集電廠及電動汽車有序充放電下的經濟調度。

3.2 算例結果分析

3.2.1 調度結果分析

上述4種場景優化調度結果見表1。

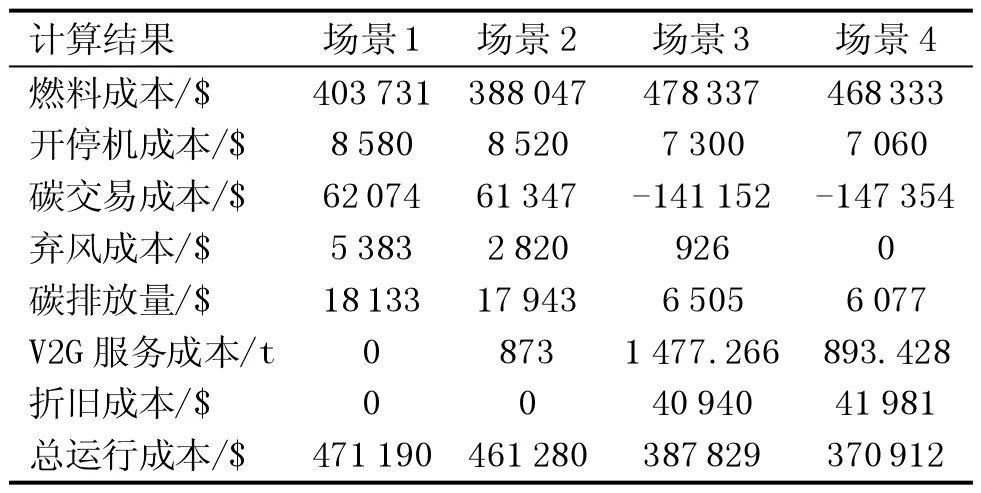
表1 4場景成本

由表1可知，場景2比場景1的燃料成本少了15 684美元，棄風成本從5 383美元下降到2 820美元，碳排放量下降了190 t，這表明電動汽車有序充放電有效消納了系統中多余的風電，使得火電機組出力減少，降低了系統碳排放量。場景3將分流式碳捕集電廠及電動汽車有序充放電相結合，場景3與場景1的對比可知，由于碳捕集系統運行過程中需要火電機組提供能量，使場景3的燃料成本有所上升，但是通過對機組產生的CO2進行捕集，火電機組的碳排放量從18 133 t下降到6 505 t，下降64.1%，使系統運行總成本下降83361美元，下降了17.6%，表明碳捕集電廠在實現系統低碳化及改善系統經濟性方面的有效性。由此可知碳捕集電廠及電動汽車有序充放電聯合模型結合了二者優勢，與單純的電動汽車有序充放電相比則具有更低的碳排放量，場景4與場景3相比，由于儲液罐的加入使得綜合靈活運行的碳捕集電廠比分流式碳捕集電廠具有更高的調峰深度、更低的機組出力下限，使風電消納能力進一步提升。而且由于儲液罐具有較低的折舊成本，使得低碳收益及風電消納收益比折舊成本多，因此總運行成本下降了169 17美元，且實現了對風電的全部消納，同時減少了系統的碳排放量。上述4個場景的對比表明本文所提模型在低碳經濟調度方面的優越性。

3.2.2 調度情況分析

在場景1中，1—3時期間負荷需求較低。考慮機組開停及機組低輸出功率下的成本，為保證總運行費用最低，系統選擇放棄一部分風電。

場景2考慮電動汽車有序充放電情況下的調度情況。可見通過電動汽車集群調度使得1—3點的負荷有所提升，這部分負荷正好可用于消納多余風電，18—19點通過電動汽車集群充電達到平滑機組出力的目的。由于電動汽車集群充放電存在上限，使得棄風情況依舊存在，但總體相較圖2有所改善。

場景3中考慮碳捕集電廠的調度情況。1—3點，由碳捕集機組承擔負荷需求，此時由于負荷需求的提升及碳捕集機組的低出力下限使得系統有更多的空間用于風電消納，從而進一步降低棄風量及碳排放量。8—12時由于高峰負荷下降使得火電機組出力降低，系統的碳排放量也跟著下降。此外8—12時、18—24時由于電動汽車集群充放電對原始負荷的影響，負荷曲線更加平滑，火電機組輸出的功率變化率更低，機組開停機次數減少，系統總運行成本降低。然而由于機組約束，3時依舊存在棄風電現象，因此仍存在優化空間。

圖1為場景4機組調度情況，場景4將分流式碳捕集電廠改為綜合靈活運行碳捕集電廠，由于碳捕集機組引入了儲液罐實現了碳捕集能耗時移。與場景3相比，場景4的4—6、10—12時碳捕集能耗轉移到1、3、9、17—24時。3時碳捕集機組需要更多能耗去進行CO2捕集，機組輸出功率降低從而實現風電完全消納。4—6時提升碳捕集機組輸出功率代替常規火電機組以滿足電動汽車充電需求。9—24時由于綜合靈活運行碳捕集電廠的能耗時移特性及更快的爬坡速率，碳捕集機組實現了負荷變化跟蹤。常規機組出力在9—17、18—24時保持穩定，有效減少了常規機組啟停次數及功率變化率。與場景3對比，場景4的模型在風電消納能力、系統低碳性及經濟性方面均有明顯優勢。

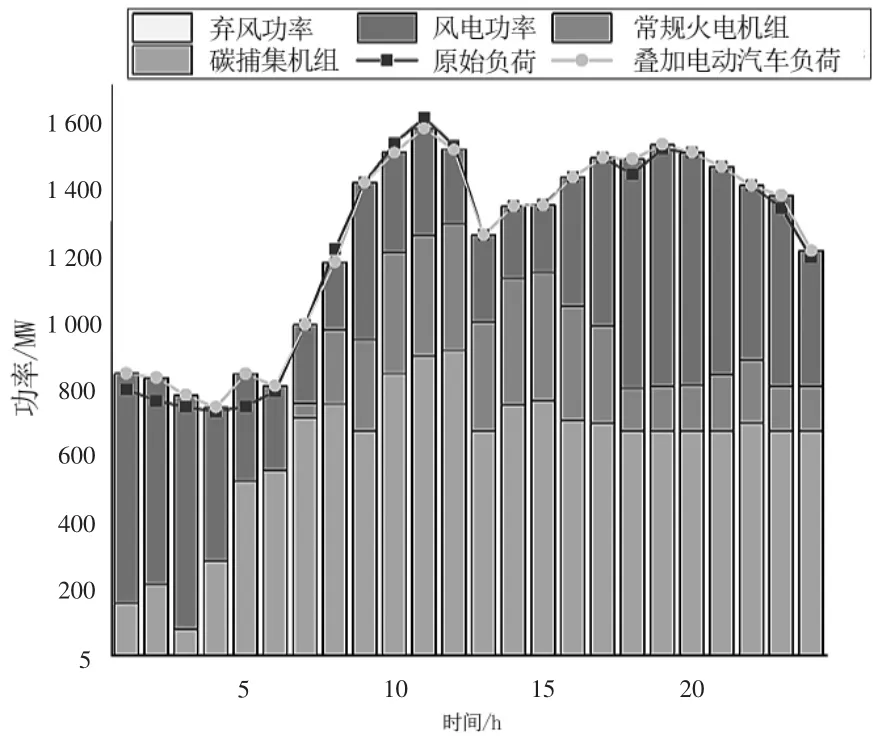
圖1 場景4機組出力

3.2.3 儲液罐體積變化分析

由于綜合靈活運行碳捕集機組的能耗時移量與儲液罐容量有關，而儲液罐容量的提升又會帶來更高的折舊成本導致系統總運行成本增加。

通過分析不同儲液罐體積下的成本和碳排量，在儲液罐體積提升至70 000 m3前，增加儲液罐體積能起到增加儲液罐能耗時移量的作用，當機組所需發電量較低時，提升此時碳捕集設備CO2處理量可以進一步減少碳排放總量。當單個儲液罐容量超過70 000 m3后碳排放量下降開始減緩，這是因為此時系統能有效捕集的CO2量已達上限，再增加儲液罐體積已無法減少系統碳排放量。在運行總費用方面，儲液罐體積小于50 000 m3時，儲液罐帶來的碳排放收益比其折舊成本要高，因此運行成本有所下降。而隨著儲液罐帶來的收益降低，后續總運行費用逐漸超過其收益使得成本不斷增加。從上述可知，通過平衡儲液罐體積、投資成本及系統總運行成本三者之間的關系，可使系統獲得最大的運行收益。

3.2.4 儲液罐溶液體積變化分析

圖2為場景4中儲液罐在不同時刻捕集的CO2變化情況。從圖2中可知1—3時儲液罐放出富溶劑捕集CO2，從而降低機組輸出功率用于消納多余風電。10—12時為負荷峰值時期，儲液罐會儲存部分CO2，減少此時間段的碳捕集能耗，從而提升碳捕集機組凈出力起到抑制常規機組的出力的作用。16—24時，此時風電出力逐漸提升，碳捕集機組出力較為充足，該情況更適于進行CO2捕集，因此儲液罐放出富溶劑用于CO2捕集。從上可知，引入儲液罐可以實現碳捕集能耗及發電之間的解耦，進一步提升碳捕集機組的碳捕集能力。

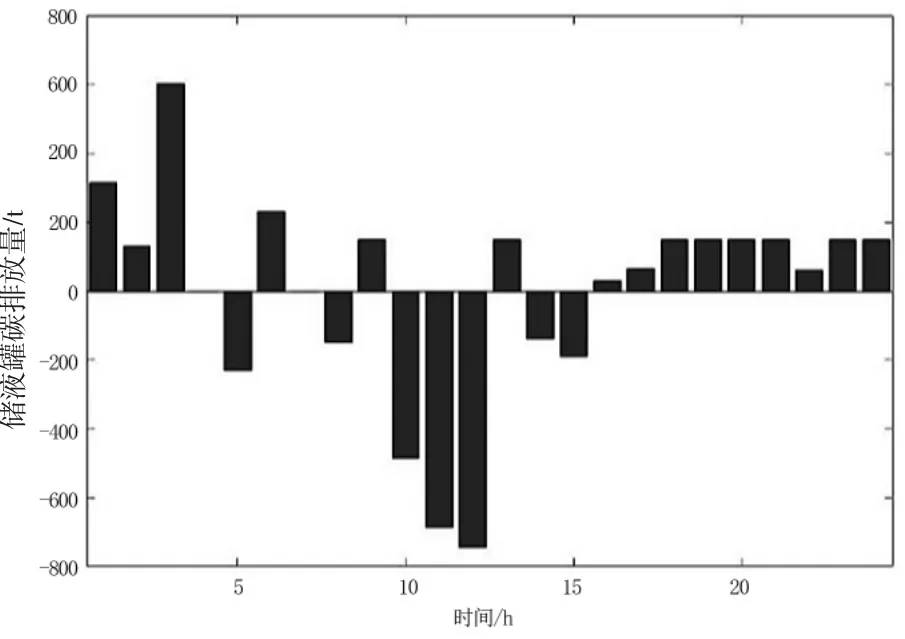
圖2 場景4下儲液罐工作情況

3.2.5 碳排放量變化分析

場景3、場景4及場景5的碳排放量變化圖，由于1—7時碳捕集機組出力較低，因此該時間段3個場景的碳排放量差距不大。場景3與場景4主要差距在10—12及18—24時，這是因為電動汽車有序充放電對負荷進行削峰填谷，使得機組出力及碳排放量更加平滑。場景5由于儲液罐碳捕集能耗平移的作用，在峰值時期碳捕集機組出力替代部分常規火力機組出力，使得碳排放量進一步減少。分析可知電動汽車有序充放電及碳捕集機組結合能有效削弱峰值時期因常規火電機組出力導致的碳排放量升高。

3.2.6 不同置信水平下運行結果分析

置信水平在0.65～0.95之間時，總運行費用均隨置信水平的增加，幾乎呈直線增長，因此風險的降低會導致運行費用的顯著提升，屬于高可靠性高投入的情況。因此考慮實際情況下可承受的最大風險程度，可得最小的系統總運行費用。

4 結論

本文建立了考慮電動汽車集群及碳捕集電廠的含風電電力系統模糊機會約束經濟調度模型，通過引入電動汽車集群以改善風電棄風現象，應用碳捕集技術對火電機組進行低碳化改造，兩方面協同作用促進電力低碳化進程。同時考慮電動汽車及風電所具有的不確定性，用模糊參數對風電及電動汽車的預測值進行描述。算例仿真結果表明電動汽車集群與碳捕集電廠協調運行能起到削峰填谷的作用，有效改善風電棄風現象，降低系統碳排放量與綜合運行成本，實現電力低碳化及經濟性發展。