基于邊界積分方程求解二維移動滾動接觸問題

舒小敏， 米棟

(中國航發湖南動力機械研究所， 株洲 412002)

工程機械中存在廣泛的移動或滾動類接觸問題。常見的移動接觸有機床中直線導軌、移動導軌等，常見的滾動接觸有機車輪軌、軸承中滾動體等。相對運動(移動或滾動)作用下產生循環接觸載荷，容易使接觸載荷影響區域內會出現接觸疲勞現象(裂紋萌生與擴展)。典型的如高速鐵路、普速鐵路和城市軌道交通中的輪軌滾動接觸疲勞，一直是研究中的技術難題之一[1]。此外工程實際中，由于兩個接觸體之間的相對運動，接觸面間將由于摩擦而產生大量的熱，進一步導致接觸表面的熱彈性變形和接觸損傷[2]。因此，接觸問題一直是研究關注的重點[3-7]。

不管是相對運動導致的接觸損傷，還是循環載荷作用下導致的接觸疲勞，接觸應力都是影響接觸損傷或接觸疲勞重要參數。求解相對運動(移動/滾動)作用下的接觸應力是研究接觸損傷或疲勞的基本條件。

工程實際中結構復雜，常見接觸解算法有：有限元法[5]、邊界元法[6]、比例邊界有限元法[7]。以上3種方法，不管采用何種方法，由于接觸體之間相對運動，即使最初采用的是匹配網格(接觸區兩接觸面節點一一對應)，相對運動(移動/滾動)后，節點將不再一一對應，變為非匹配網格。非匹配網格中不能保證全局平衡，可能會出現壓力波動問題[8]，影響接觸應力計算精度。

減少壓力波動的直接方法是將非匹配網格變成匹配網格。在邊界元法接觸分析中，文獻[9]采用了可動節點法，可保證移動或滾動后節點一一對應。不過，由于相對位置的變化，積分單元中出現相距很近的兩節點將難以避免，在邊界積分中將引入奇異積分難題。在有限元法接觸分析中，文獻[10-12]采用了可變節點的單元，實現節點一一對應，并應用到彈塑接觸性問題及大變形接觸問題中。比例邊界有限元法中，文獻[13-14]通過插入節點的方法在準靜態接觸問題中實現節點一一對應，而文獻[15]采用自適應網格法減少壓力波動。文獻[10-15]中的方法，目前還未推廣到移動或滾動接觸中。

相對運動過程中，可能接觸區位置一直變化，為精確模擬接觸區應力集中現象，則需對所有可能接觸區進行網格加密。以移動接觸問題為例，在移動過程中可能接觸區不斷變化。為精確模擬移動接觸過程中接觸區的應力集中現象，需對移動過程中所有可能接觸區進行網格加密。而實際移動過程中，某一時刻的可能接觸區卻遠小于所有可能接觸區，大范圍的網格加密影響計算效率、增加計算成本。

為解決移動或滾動滾動接觸中，非匹配網格引起的接觸壓力波動及避免在所有可能接觸區進行網格加密，現采用網格更新法[16]保證接觸區網格一一對應，并保證僅當前時刻可能接觸區網格需加密。為減少網格更新數量，本文研究采用邊界積分方程求解，這是由于邊界積分方程中僅邊界網格需離散[17-18]。為避免移動滾動后邊界積分重復計算，本文研究采用旋轉坐標系法，推導出移動滾動前后時刻邊界積分方程的等價性，結果只需對更新的單元和節點進行積分，其他積分可直接利用上一時刻的積分數據。基于以上方法，本文研究提出二維移動滾動接觸問題解方法，并通過數值算例驗證本文方法的有效性。

1 邊界積分方程的等價

1.1 邊界積分方程

對于彈性問題，在不考慮體力的情況下，每個體的邊界積分方程[17-18]為

P，Q∈Γ

(1)

式(1)中：uj和tj分別為位移和面力分量；Uij和Tij分別為位移和面力核函數或基本解；cij(P)為關于體邊界Γ布置系數矩陣；P、Q為物體邊界Γ上的點。

在二維(i，j=1，2)平面應變問題中，位移和面力基本解對應表達式為

(2)

(3)

式中：r為源點P到場點Q的向量；r為點P和Q之間的長度;n為場點Q處的外法向；ri和ni為向量r和n的在i方向的導數；δij為克羅內克函數；G和v分別為剪切模量和泊松比，彈性問題中其值大小不變。

1.2 邊界積分方程等價

邊界積分方程等價，根據式(1)～式(3)要求源點P和場點Q之間的向量r無變化，同時Q處的外法向n不變。

如果坐標系不變，即不同時刻采用相同的坐標系。如圖1所示，按w角速度滾動的物體，在不同時刻，若均采用時刻a的xa-o-ya坐標系，那么時刻a和時刻b比較，源點P到場點Q的向量r及場點Q處的外法向n均發生變化，邊界積分方程不等價。因此，b時刻需要重新計算邊界積分。

采用旋轉坐標系法，即坐標系隨物體一起旋轉，則可推導出邊界積分方程等價。即在圖1中a時刻采用坐標系xa-o-ya，而b時刻采用坐標系xb-o-yb，那么a和b時刻比較，源點P到場點Q之間的向量r沒有變化，且場點Q處的外法向n無變化。因此a時刻和b時刻邊界積分方程完全等價，b時刻的邊界積分可直接使用a時刻積分數據。

對于移動體問題，在圖2中移動體以速度v0運動，同樣采用旋轉坐標系法，a時刻采用坐標系xa-o-ya，而b時刻采用坐標系xb-o-yb。由于無旋轉，坐標系方向不變。a時刻和b時刻源點P到場點Q之間的向量r無變化，且場點Q處的外法向n無變化，因此a時刻和b時刻邊界積分方程完全等價。

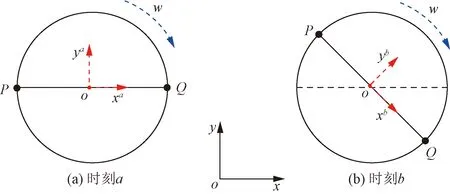
圖1 不同時刻滾動示意圖Fig.1 Rolling diagrams at different moments

圖2 不同時刻移動示意圖Fig.2 Sliding diagrams at different moments

采用旋轉坐標系法，如果網格離散相同，移動或滾動下一時刻則可利用上一時刻的邊界積分數據，避免各時刻重新計算邊界積分。

2 接觸描述及坐標更新

2.1 接觸點對法向坐標定義

考慮如圖3所示兩接觸體邊界上的接觸點對，即a和b，接觸區的公共法向量定義為

(4)

式(4)中：EA、EB分別為接觸體A、B的楊氏模量；nA和nB為接觸點a、b處的法向量。

切向量τ可通過旋轉法向量90°得到。接觸點對由最近投影點決定。在本文研究中，剛度較小接觸體上的節點投影到另一剛度較大的接觸體上，更大剛度體的法向量用于決定最近投影點。公共法向量僅用于確定接觸區面力和位移的法向方向，并不用于確定最近投影點。

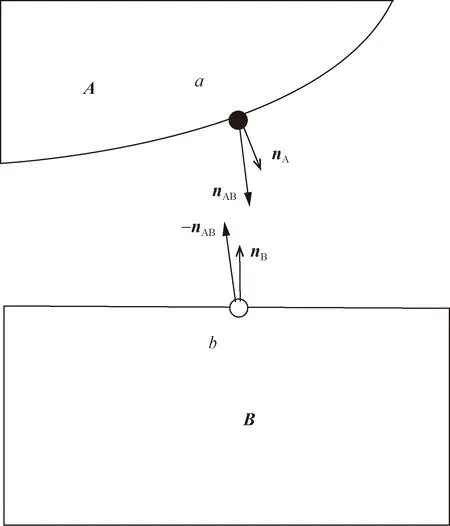
圖3 公共接觸法向量定義Fig.3 Definition of the common contact direction

2.2 無摩擦接觸約束

在無摩擦接觸中，可能接觸區只有非接觸和滑移接觸狀態存在。對于非接觸狀態，法向和切向面力均為零。

(5)

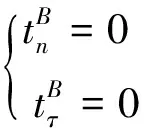
(6)

對于滑移接觸狀態，法向間隙為零，切向面力為零；此外節點對上的面力大小相等：

(7)

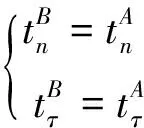
(8)

式中：uj和tj為加載后位移和面力，其中j=n,τ；A、B為對應的接觸體；g為初始法向間隙。

2.3 坐標更新

采用旋轉坐標系法，即坐標系隨物體一起旋轉，可保證單個體的邊界積分方程在移動或滾動前后時刻的等價性。不過在接觸問題中，需建立接觸約束關系如式(7)所示，而接觸約束關系的建立需要在一個統一的坐標系下描述。因此，移動滾動后需對坐標進行更新。

2.3.1 移動坐標更新

如圖2所示，若移動的距離為L，移動的單位方向向量為(vx，vy)，則移動后的點坐標為初始坐標值(x，y)加上其在移動方向的移動距離，坐標值更新可表示為

(9)

2.3.2 定軸轉動坐標更新

如圖4所示，假設點A繞圓心C轉動，坐標(xc,yc)則點A相對于圓心C的坐標為

(10)

式(10)中：R為定軸轉動半徑；α為點A相對于水平位置的夾角，如圖4所示。點A轉動θ角之后到達點A′的位置，它相對于圓心C的坐標為

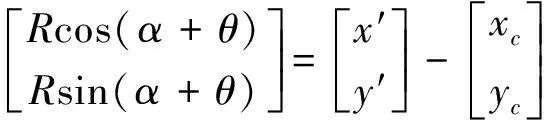
(11)

點A′相對于圓心C的坐標可寫為

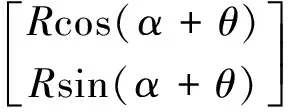
(12)

將(Rcosα，Rsinα)用點A的坐標公式[式(10)]代替，則點A′相對于坐標原點O的坐標為

(13)

式(13)即為定軸轉動一定角度后點的坐標值。只要知道定軸轉動中心、初始點坐標及轉動角度，利用該公式就可進行坐標更新。

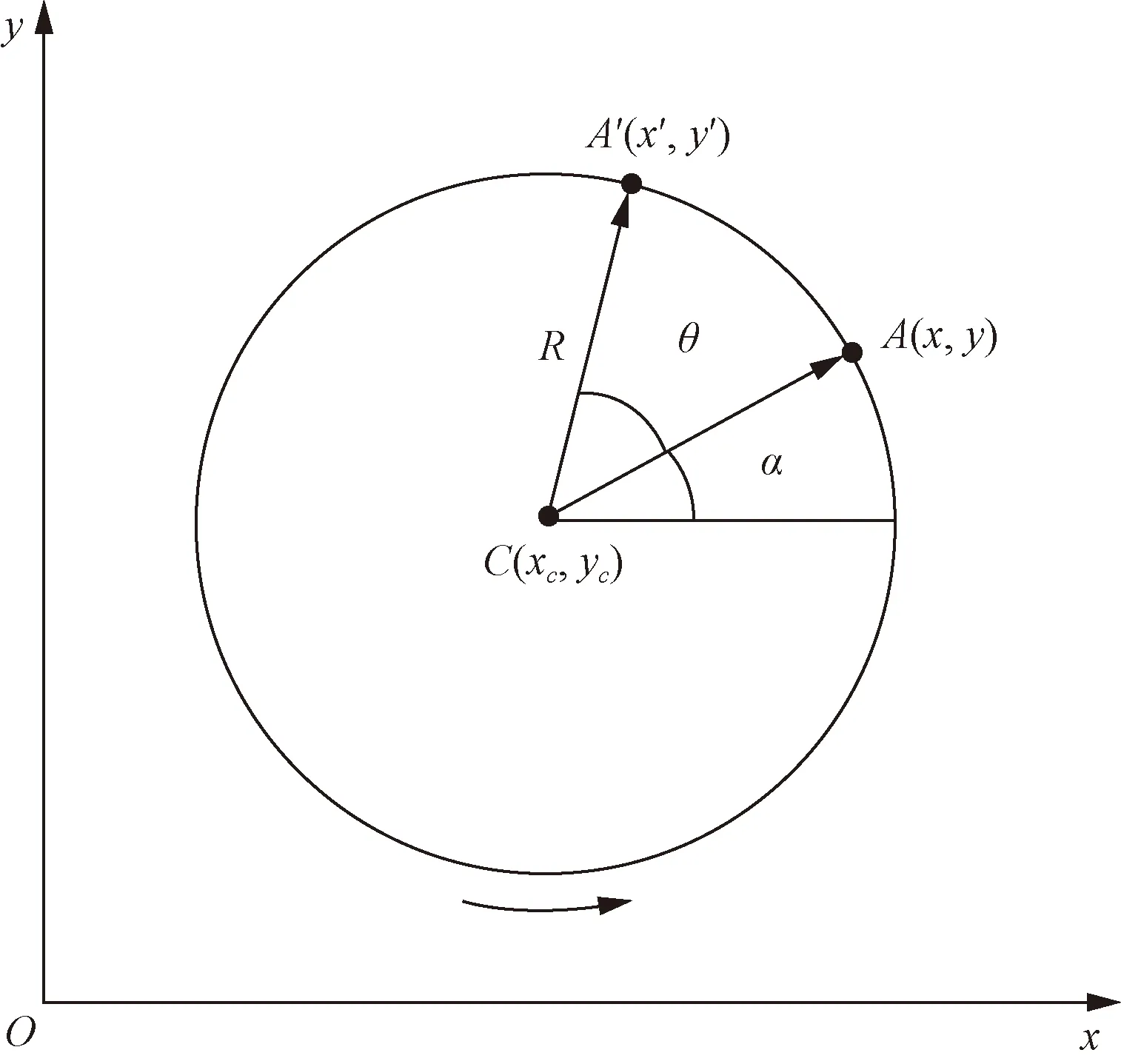
圖4 定軸轉動Fig.4 Fixed axis rotation

2.3.3 滾動坐標更新內容

滾動具有定軸轉動的特點又有移動，它等價于在定軸轉動基礎上再加上移動。滾動后的坐標更新需結合式(9)和式(13)，坐標更新公式為

(14)

3 網格更新及其積分計算

3.1 網格更新法

圖5為滾動接觸相鄰兩時刻的可能接觸區(陰影部分)。圖5(a)對應上一時刻，可能接觸區為e。圖5(b)對應當前時刻，可能接觸區為f。從圖5(b)中可看出，當前時刻是上一時刻點A′運動到點A的狀態。在當前時刻中，既存在當前時刻的可能接觸區f，也存在上一時刻的可能接觸區e。

網格更新中，保證僅當前時刻可能接觸區網格需加密。因此對于當前時刻，可能接觸區f的網格需要加密更新。同時當前時刻中，上一時刻的可能接觸區e不再是可能接觸區，網格不需要加密處理。因此當前時刻中，上一時刻的可能接觸區e的加密網格需變為一般網格，網格需更新。

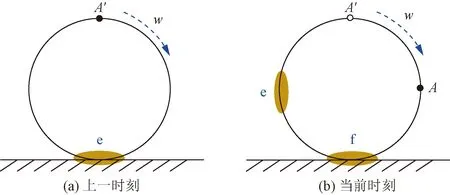
圖5 滾動前后接觸區域變化Fig.5 The changes in potential contact area after rolling

總之，網格更新就是將上一時刻可能接觸區的加密網格更新為一般網格；同時將當前時刻可能接觸區網格更新為加密網格。采用該方法后，僅當前時刻可能接觸區的網格進行了加密。不會在移動或滾動多次后，網格不斷增加。

3.2 積分計算

采用網格更新法后，部分網格單元進行了更新，即網格單元發生了變化，這些更新網格單元對應的積分仍需重新計算。

首先，根據單元更新情況，將離散后的節點分為新節點和舊節點。舊節點的定義為：節點在單元中的位置沒有變化且與該節點相連的單元也無變化。其他不滿足舊節點定義的節點，則為新節點。為說明這一定義，用圖6進行闡述。

在圖6所示的網格更新中，單元α和β更新為4個子單元α1、α2、β1和β2。更新后所有實心圓點為舊節點，新節點用空心圓點表示。節點P和Q位置雖然無變化，但與其相連的單元變化了。根據新舊節點定義，P和Q為新節點。

其次，根據新舊節點定義新舊單元。舊單元的定義為：全部為舊節點的單元。其他不滿足舊單元定義的單元為新單元。

采用旋轉坐標系法，舊單元和舊節點對應的積分系數可從上一時刻的積分數據中提取。因此，網格更新后，只需重新計算新節點和新單元對應的邊界積分。不過，并非所有時刻都存在著上一時刻。最初計算時，沒有上一時刻。因此，最初時刻中將所有的單元和節點全部定義為新單元和新節點，這時所有的單元都要進行積分計算。通過此次計算，存儲相關積分數據。以后時刻網格無變化，則可利用上一時刻的積分數據，避免重復計算積分。

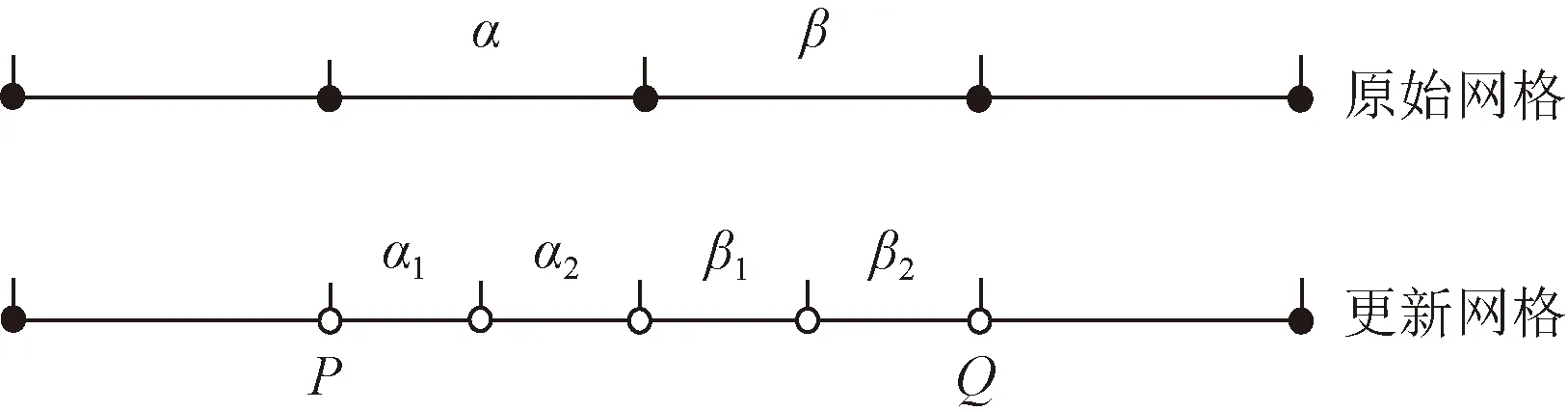
圖6 網格更新示意圖Fig.6 Schematic diagram of mesh updating

4 移動滾動接觸算法流程圖

圖7為本文移動滾動接觸問題解算法流程圖。接觸求解具體可參考文獻[6，19]，運動是否終止為用戶輸入參數。

采用圖7中算法求解移動滾動接觸問題，主要優勢如下：利用網格更新，保證僅當前時刻可能接觸區網格需加密，同時實現接觸區節點一一對應(匹配網格)，避免接觸區壓力波動問題[8]。此外采用旋轉坐標系法，移動滾動前后時刻邊界積分方程等價，避免未更新網格移動滾動后積分重復計算。

圖7 移動滾動接觸算法流程圖Fig.7 Algorithm flowchart for sliding or rolling contact problems

5 數值算例

本節給出了兩個無摩擦數值算例，用于證明本文方法的有效性。第一個是移動Hertz接觸問題，另一個為滾動接觸問題。

5.1 移動Hertz接觸

如圖8所示，一個彈性半圓(半徑R=8 mm)在一個剛性體表面勻速移動。計算中取剛性體楊氏模量為彈性體楊氏模量的十萬倍，此時可完全等價為剛性體。幾何尺寸、邊界條件、楊氏模量E、泊松比μ和載荷p情況如圖8所示。

圖8所示的無摩擦問題，有解析解存在[4]。根據解析解，接觸半寬b的計算公式為

(15)

而接觸法向壓力pn的計算公式為

(16)

根據圖8中的材料及載荷參數，接觸半寬b=0.544 6 mm。本文方法和解析解對比如圖9所示。

雖然半圓向前移動了一段距離(L=1，2，3，4 mm)，但圖9中本文方法所有接觸壓力結果完全一

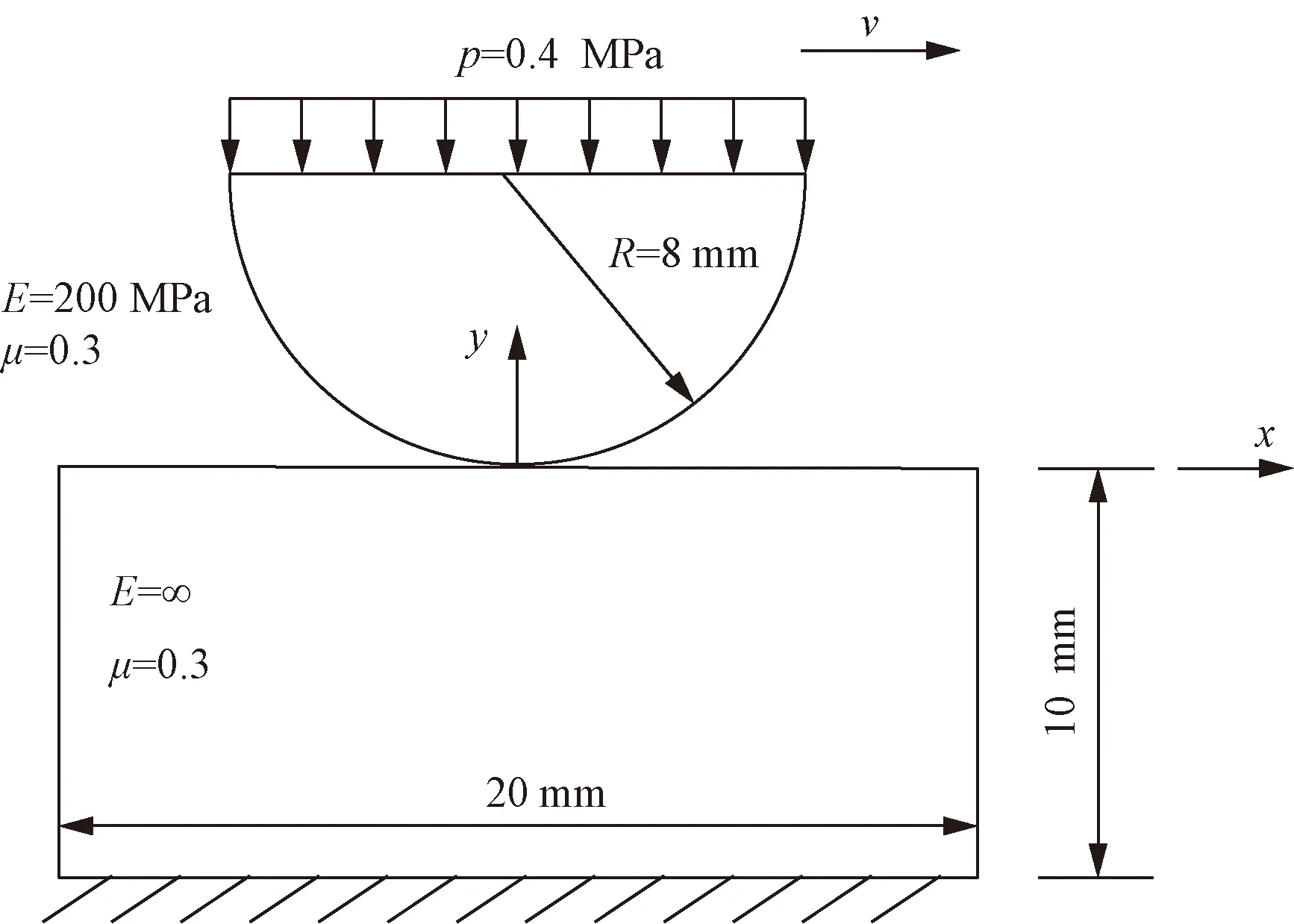
圖8 Hertz接觸問題Fig.8 Hertz contact problem

圖9 移動不同距離的接觸壓力圖Fig.9 Contact pressure plots with different sliding distances

致。這是由于另一接觸體為剛性體，在剛性體表面上移動，任意位置的接觸壓力是相同的。此外圖9中解析解和本文方法結果幾乎完全重合，表明在移動接觸問題中，本文網格更新法及邊界積分等價法的有效性及準確性。

5.2 滾動接觸

如圖10所示，一個空心圓輪(半徑R=5 mm)在一個拱形基座上勻速滾動，幾何尺寸在圖10中給出。黑色實線空心圓輪對應著初始時刻；紅色虛線圓輪對應著滾動距離L=6 mm時的圓輪，此時模型對稱。兩接觸體的材料參數相同：楊氏模量E=2 000 MPa、泊松比μ=0.3。邊界條件為：基座兩底端平面固定，載荷施加在空心圓輪孔的下半部分，壓力大小為

(17)

式(17)中：x和y為滾動更新后坐標值；L為滾動距離，初始時刻L=0。該載荷公式的含義是只有空心圓輪孔的下半部分承受壓力載荷，且滾動中下半部分承受載荷相同。

計算了滾動距離L=0、3、6 mm時的應力分量(Syy)，結果如圖11所示。此外為證明本文方法的有效性，計算了若初始時刻L0=6 mm(等價于滾動距離L=6 mm)的應力，如圖12所示。

滾動距離L從0～6 mm，接觸中心逐漸逼近拱形基座對稱面，且L=6 mm時接觸中心與基座半圓之間厚度最小。對于相同載荷，接觸中心與基座半圓間y方向厚度越小，引起的變形更大，應力越大。

圖10 滾動接觸幾何模型Fig.10 Geometric model of rolling contact

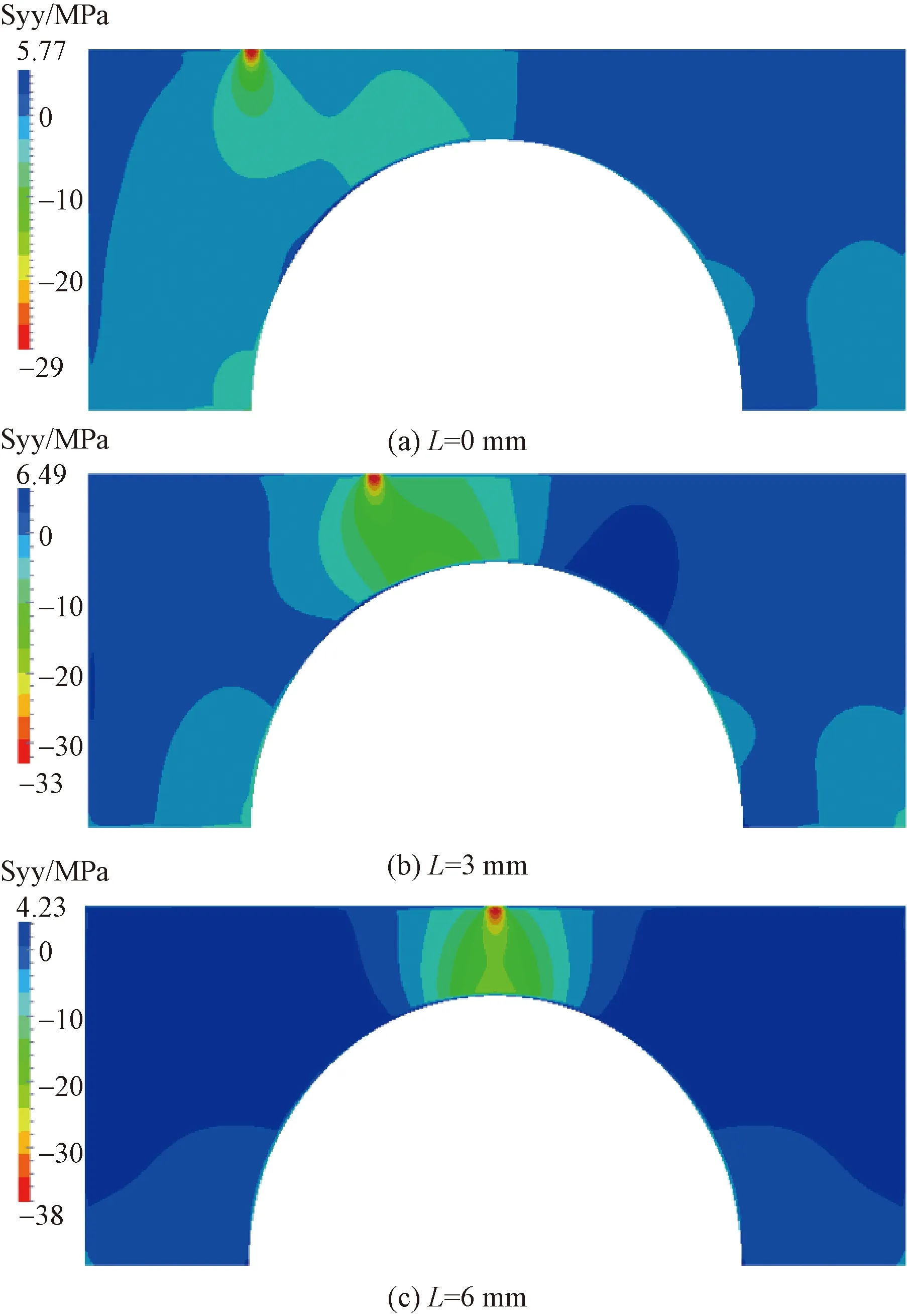
圖11 不同時刻應力圖Fig.11 Stress map at different moment

圖12 初始時刻L0=6 mm的應力圖Fig.12 Stress map at the initial time L0=6 mm

從圖11可看出，隨著接觸中心與基座半圓間y方向厚度越來越小，接觸中心處應力值逐漸增大，符合預測。

圖12為若初始時刻L0=6 mm的應力圖，此時模型和載荷對稱，應力結果應對稱。從圖11(c)中可看出，采用本文方法滾動L=6 mm時的應力結果不僅對稱，而且該結果與圖12應力云圖幾乎完全一致，表明在滾動接觸問題中，本文網格更新法及邊界積分等價法的有效性及準確性。

6 結論

基于邊界積分方程法對移動或滾動接觸問題進行了求解，得出如下結論。

(1)采用網格更新法，保證僅當前時刻可能接觸區網格需加密，從而避免了移動或滾動過程中所有可能接觸區都需要網格加密的問題；并保證了接觸區節點一一對應，保證接觸應力的精度。

(2)采用旋轉坐標系法，推導出了移動或滾動前后時刻邊界積分方程的等價性。因此，下一時刻積分計算可直接利用上一時刻的積分系數，減少積分重復計算量。

(3)基于網格更新法、旋轉坐標系法和邊界積分方程法提出了移動或滾動接觸問題解方法，并利用數值算例證明了本文方法的有效性。

(4)雖然本文研究局限于二維移動滾動接觸問題，但本文方法卻并不局限于二維問題，可推廣到三維移動滾動接觸。