基于虛擬區(qū)域法的黏彈性流體中微生物游動的數(shù)值模擬和應(yīng)用1)
彭方遠(yuǎn) 潘定一 陳杏藩 林昭武,2)
* (浙江大學(xué)工程力學(xué)系,杭州 310027)
? (浙江大學(xué)光電科學(xué)與工程學(xué)院,杭州 310027)
引言
研究微生物游動的行為特征以及動力學(xué)機(jī)理,具有重要的理論意義和應(yīng)用價(jià)值.微生物作為自然界生態(tài)系統(tǒng)的重要組成部分,分解各種有機(jī)物,直接參與物質(zhì)循環(huán),例如海洋中的微生物為全球提供了大量的氧氣,供人類生產(chǎn)生活[1].此外,細(xì)菌類微生物聚集能夠形成生物膜,可以利用其進(jìn)行廢水處理,但也容易造成食品污染等不利后果[2].隨著科學(xué)技術(shù)的飛速發(fā)展,模仿微生物的人工微型器件廣泛應(yīng)用于各個(gè)領(lǐng)域.例如Karshalev 等[3]利用涂有二氧化鈦的“鎂微球”,證明了鐵和硒礦物質(zhì)可以用于治療貧血.Zhang 等[4]利用“微型器件”監(jiān)測傳感電化學(xué)信號,并應(yīng)用于臨床診斷、藥物運(yùn)輸?shù)确矫?Vysko?il等[5]利用“微型機(jī)器人”,可以在不破壞細(xì)胞膜的情況下進(jìn)入癌細(xì)胞,拓展了癌癥的治療方法.由此可見,深入研究微生物的行為特征,了解并掌握微生物在復(fù)雜流體中的運(yùn)動特性,具有重要研究價(jià)值,并且可以為微型器件的設(shè)計(jì)制造提供理論指導(dǎo).
鑒于以上原因,微生物游動問題受到越來越多的關(guān)注.其中,壁面效應(yīng)是微生物游動研究中的重要問題之一.已有研究表明,微生物在壁面附近存在復(fù)雜的行為特征[6-14],例如: 團(tuán)藻在壁面附近的“跳舞”行為,公牛精子和衣藻在近壁處的散射行為,大腸桿菌在固壁面附近沿順時(shí)針繞圈的行為[6-8].Kuron 等[9]采用數(shù)值方法研究牛頓流體中微生物在平面以及曲面壁面附近的行為特性,發(fā)現(xiàn)了散射、向前翻滾、向后翻滾和懸停等四種行為.Chaithanya 等[10]初步分析了壁面曲率對微生物行為的影響規(guī)律,其結(jié)果表明牛頓流體中微生物更容易被凹形曲面吸引.Ishimoto 等[11]的研究結(jié)果表明,牛頓流體中壁面的拓?fù)浣Y(jié)構(gòu)對于引導(dǎo)微生物的定向運(yùn)動有一定的作用.Narinder 等[12-13]采用實(shí)驗(yàn)手段,利用人工合成感光粒子模擬微生物,發(fā)現(xiàn)與牛頓流體相比,粒子在黏彈性流體近壁處的速度明顯減小;而且由于流體彈性,粒子會繞開彎曲壁面.Li 等[14]采用數(shù)值方法,研究了黏彈性流體中微生物近壁處的行為特征,發(fā)現(xiàn)不同類型微生物具有不一樣的運(yùn)動特性.Ouyang等[15]采用浸沒邊界?格子波爾茲曼方法,研究了冪律流體中微生物近壁處的行為特性,發(fā)現(xiàn)隨著冪律流體指數(shù)的變化,不同種類的微生物表現(xiàn)出的行為特性具有一定的差異性.Ahana 等[16]采用數(shù)值模擬的方法,研究發(fā)現(xiàn)與非近壁相比,微生物在近壁處的平動速度較少,而角速度卻較大.Leoni 等[17]實(shí)驗(yàn)研究了兩種不同類型的微生物在曲壁面附近的行為特性,發(fā)現(xiàn)了三種形態(tài),且微生物都更為集中地在壁面附近運(yùn)動.Yazdi 等[18]運(yùn)用數(shù)值方法研究了Oldroyd-B流體中微生物的游動行為,發(fā)現(xiàn)微生物與壁面的初始距離對微生物壁面效應(yīng)有較大影響.
總體而言,已有研究工作大多集中于牛頓流體領(lǐng)域,僅有少數(shù)涉及黏彈性流體等非牛頓流體領(lǐng)域.這主要是因?yàn)? 一方面黏彈性流體等非牛頓流體的流動行為比較復(fù)雜;另一方面求解黏彈性流體本構(gòu)方程具有一定的難度,對算法精度和穩(wěn)定性都有很高的要求[19].
對于算法穩(wěn)定性,已有文獻(xiàn)提出顯式求解、迭代求解、額外增加人工耗散項(xiàng)以及限制構(gòu)型張量特征值等方法[20-23].對于對流項(xiàng)的離散,為了保證其精度,已有研究工作提出迎風(fēng)格式、TVD(total variation diminishing) 格式、MUSCL(monotone upstreamcentered schemes for conservation laws)格式以及WENO(weighted essentially non-oscillatory)格式等[24-26].對于構(gòu)型張量的求解,文獻(xiàn)中提出了對構(gòu)型張量進(jìn)行一系列的變換以保證其對稱正定性質(zhì),如:對數(shù)函數(shù)變換、平方根分解以及喬列斯基分解等[23,27-28].上述方法一定程度上保證了算法的精度以及穩(wěn)定性.但是,文獻(xiàn)[19] 同樣指出,對于高Reynolds 數(shù)以及大Weissenberg 數(shù)的工況,現(xiàn)有數(shù)值算法仍面臨巨大的挑戰(zhàn).
有鑒于此,本文對求解黏彈性流體的數(shù)值算法進(jìn)行初步探索,并將其應(yīng)用于研究微生物游動過程的壁面效應(yīng).本文余下內(nèi)容組織如下: 第1 節(jié)介紹數(shù)學(xué)模型以及數(shù)值算法;第2 節(jié)進(jìn)行算法驗(yàn)證;第3 節(jié)給出模擬結(jié)果并進(jìn)行機(jī)理分析;最后第4 節(jié)給出本文結(jié)論以及后續(xù)工作展望.
1 模型和方法
本文所模擬的對象涉及運(yùn)動邊界等問題,為了處理相應(yīng)的流固耦合問題,本文采用虛擬區(qū)域方法(fictitious domain method),將問題分解為流體子問題、微生物運(yùn)動子問題以及黏彈性流體本構(gòu)方程子問題進(jìn)行求解.總體而言,在模型方面,微生物運(yùn)動采用經(jīng)典的Squirmer 模型,而黏彈性流體則采用Giesekus 模型;在黏彈性流體本構(gòu)方程的數(shù)值求解方面,則采用顯式格式結(jié)合喬列斯基分解進(jìn)行求解.以下分小節(jié)詳細(xì)介紹.
1.1 微生物模型
Squirmer 模型是一種經(jīng)典的微生物水動力模型,最早由Lighthill[29]和Blake[30]提出.該模型將微生物視為球形剛性顆粒,其表面具有給定的速度分布
式中e為顆粒的游動方向,r為徑矢,Pn為n階勒讓德多項(xiàng)式(Legendre),n為階模態(tài)系數(shù).與大多數(shù)已有文獻(xiàn)相同,本文采用前兩階模態(tài),即
其中,角度 θ=arccos(e·r/r),表示位置徑矢與運(yùn)動方向的夾角;B1和B2是前兩階模態(tài)的系數(shù).通過比值U0=2B1/3 來區(qū)分粒子的類型,β >0時(shí)為拉動型粒子(puller),β <0 時(shí)為推動型粒子(pusher),β=0時(shí)為中性粒子(neutral).在Stokes 流中,粒子的穩(wěn)定游動速度為U0=2B1/3.
由于采用虛擬區(qū)域方法進(jìn)行數(shù)值模擬的緣故,需要將式(2)延拓到整個(gè)球體,于是采用Li 等[31-33]提出的速度分布模型
其中a是球型顆粒的半徑,er和eθ是沿r和θ方向的單位向量,m是任意正整數(shù).當(dāng)r=a時(shí),式(3)符合式(2)的速度分布.
1.2 流體黏彈性模型
本文采用經(jīng)典的Giesekus 黏彈性本構(gòu)模型[34],黏彈性流體中聚合物的應(yīng)力貢獻(xiàn)為
其中 λt表示聚合物的弛豫時(shí)間,μp表示聚合物黏度,C為構(gòu)型張量,具有對稱正定性質(zhì).構(gòu)型張量的本構(gòu)方程為
其中 α為模型參數(shù),表征聚合物受到的各向異性水動力,其取值范圍為 0 ~0.2.α=0時(shí),Giesekus 模型退化為黏度為常數(shù)的Oldroyld-B 黏彈性模型.方程(5)的求解難點(diǎn)在于: (1)方程的非線性性質(zhì);(2)保證構(gòu)型張量C的對稱正定性質(zhì);(3)對流項(xiàng)的離散.其求解方法將在1.4 數(shù)值格式部分詳細(xì)介紹.
1.3 虛擬區(qū)域法
虛擬區(qū)域方法屬于非貼體網(wǎng)格法,最早由Glowinski 等[35]提出,其核心思想是假設(shè)固體顆粒內(nèi)部充滿虛擬流體,對內(nèi)部的虛擬流體作用一個(gè)擬體力(也稱為拉格朗日乘子),使其運(yùn)動滿足剛體運(yùn)動的約束.在此基礎(chǔ)上Yu 等[36-37]發(fā)展了虛擬區(qū)域方法,提出了直接力格式,并將算法并行化.文獻(xiàn)[37-40]將該方法應(yīng)用于研究顆粒湍流問題,并取得了一系列進(jìn)展.近年來,本文作者Lin 等[33]進(jìn)一步拓展該方法,將其成功應(yīng)用于研究牛頓流體中微生物的游動問題.虛擬區(qū)域法求解的無量綱形式的控制方程如下
1.4 數(shù)值格式
在求解流體控制方程時(shí),本文采用時(shí)間步分裂格式[33,36],將方程式(6)~ 式(11)解耦為流體運(yùn)動、微生物顆粒運(yùn)動以及黏彈性流體本構(gòu)方程等三個(gè)子問題.
(1)流體運(yùn)動子問題,求解u?和pn+1
采用投影格式將速度和壓力解耦求解上述方程組,即
①速度亥姆霍茲(Helmholtz)方程
②壓力泊松(Poisson)方程
③速度和壓力修正方程
流場采用半交錯(cuò)均勻網(wǎng)格,空間導(dǎo)數(shù)離散采用二階中心差分格式;速度方程(14) 與壓力方程(15)采用多重網(wǎng)格迭代法進(jìn)行求解.
將方程式(18)~ 式(19)代入式(20)~ 式(21)可以得到
最后,流體速度求解如下
上述方程的求解,涉及物理量在不同網(wǎng)格間的轉(zhuǎn)換.本文采用三線性插值函數(shù)作為離散Delta 函數(shù)實(shí)現(xiàn)物理量在歐拉網(wǎng)格節(jié)點(diǎn)x和拉格朗日網(wǎng)格節(jié)點(diǎn)X之間的轉(zhuǎn)換.
式中h為網(wǎng)格步長,ψ函數(shù)為線性函數(shù)
(3)黏彈性流體本構(gòu)方程子問題,求解Cn+1
記構(gòu)型張量及速度的分量形式為
本文采用Vaithianathan 等[23]提出的數(shù)值方法求解黏彈性流體本構(gòu)方程(11).利用喬列斯基方法分解構(gòu)型張量C可以得到
將構(gòu)型張量C的求解轉(zhuǎn)化為對張量L的求解,只要張量L的對角元素滿足條件l11,l22,l33>0,即可保證其對稱正定性質(zhì).進(jìn)一步對對角元素采用指數(shù)函數(shù)替換
將式(28)和式(29)代入方程(11),可以得到
利用已更新的速度un+1,對新方程(30)采用顯式求解.對流項(xiàng)采用高精度的MUSCL 格式離散;時(shí)間積分采用四階龍格庫塔方法;從而保證算法具有良好的數(shù)值精度以及穩(wěn)定性.
1.5 碰撞模型
本文研究的問題還涉及微生物顆粒與平面壁面的接觸問題,因此引入軟球碰撞模型,對壁面附近的剛體顆粒施加一定的排斥力,從而使得顆粒與壁面之間避免重疊.該模型如下[33,37]
其中F0為給定常數(shù),d是顆粒與壁面間的距離,dc是判斷“接觸”與否的截?cái)嗑嚯x,n是接觸方向的單位向量.本文設(shè)置F0=1.0×(104~105),dc=h~2h.最后更新顆粒位置
由于方程式(31)~ 式(32)采用顯式求解,所以要求更小的時(shí)間步長,本文選取為 ?t/10.
1.6 算法并行化實(shí)現(xiàn)
本文采用區(qū)域分解策略,基于消息傳遞接口MPI 實(shí)現(xiàn)虛擬區(qū)域方法的并行編程.本文作者Lin 等[37]已經(jīng)實(shí)現(xiàn)了針對牛頓流體的并行虛擬區(qū)域方法.在此基礎(chǔ)上,需要對黏彈性流體本構(gòu)方程的求解并行化處理.其難點(diǎn)在于對流項(xiàng)的高精度離散格式,每個(gè)子區(qū)域需要兩層或者更多的額外單元,用于存儲其他子區(qū)域交換過來的網(wǎng)格信息.
如圖1 所示,以二維計(jì)算區(qū)域?yàn)槔?藍(lán)色部分代表當(dāng)前進(jìn)程‘管理’的子區(qū)域,由于離散格式的要求,需要獲得邊界附近區(qū)域紅色以及綠色部分的網(wǎng)格信息,例如流體速度和構(gòu)型張量.本文采用以下策略實(shí)現(xiàn)該過程: (1)在區(qū)域“1”的基礎(chǔ)上,通過數(shù)據(jù)交換先獲得紅色區(qū)域的網(wǎng)格信息;(2)在區(qū)域“2”的基礎(chǔ)上,重復(fù)(1) 步驟獲得綠色區(qū)域的網(wǎng)格信息.以此類推,通過重復(fù)(1)步驟可以獲得更多層以上的網(wǎng)格信息,從而滿足離散格式的需求.更多細(xì)節(jié)請參考文獻(xiàn)[37].
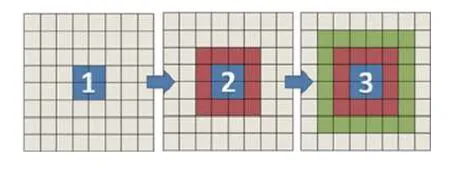
圖1 網(wǎng)格信息交換示意圖Fig.1 Schematic of data exchange
最后,如圖2 所示,給出針對黏彈性流體的并行虛擬區(qū)域方法的算法流程圖.
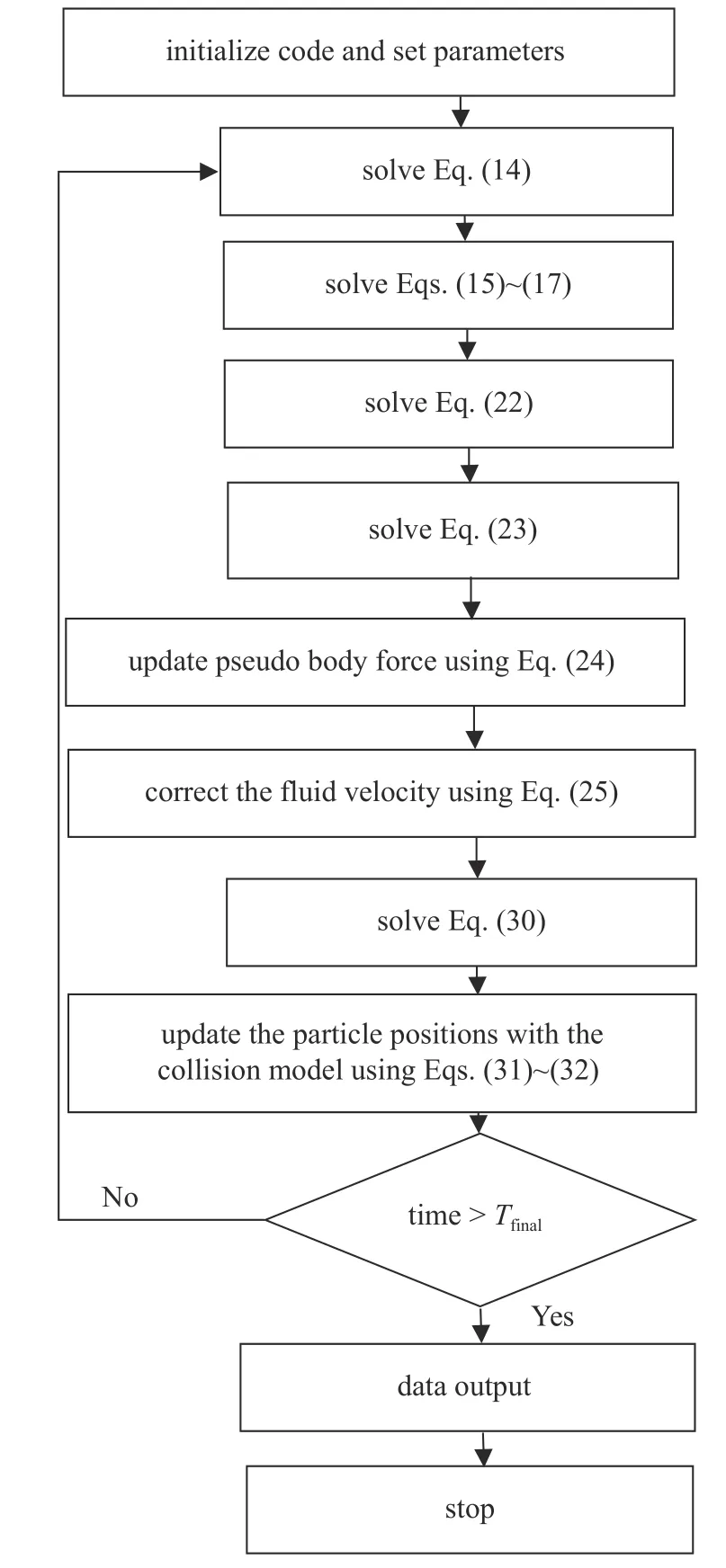
圖2 并行虛擬區(qū)域法流程圖Fig.2 Flowchart for the parallel fictitious domain method
2 算法驗(yàn)證
針對牛頓流體的并行虛擬區(qū)域方法在文獻(xiàn)中已有大量的驗(yàn)證[33,37-40].在此基礎(chǔ)上,進(jìn)行本文算法精度驗(yàn)證.選取文獻(xiàn)[14,41]的結(jié)果進(jìn)行對比,按照文獻(xiàn)選取工況參數(shù)如下: Reynolds 數(shù)Re=0.01;模型參數(shù) α=0.2,μr=0.5,We=0 ~4;粒子類 型β=5,?5,假定微生物顆粒與流體密度接近,即 ρr=1.0.計(jì)算區(qū)域大小為16 × 16 × 16,網(wǎng)格規(guī)模256 × 256 × 256,網(wǎng)格步長h=1/16,典型時(shí)間步長為 ?t=0.000 5 ~0.002.計(jì)算區(qū)域三個(gè)方向均設(shè)置為周期性邊界條件.
如圖3 所示,微生物顆粒自由游動,充分發(fā)展后兩種類型粒子的平均速度UGK與文獻(xiàn)[14,41]的結(jié)果吻合,驗(yàn)證了本文算法精度的可靠性.在此基礎(chǔ)上,進(jìn)行網(wǎng)格收斂性分析.圖3(b)插圖給出粗細(xì)兩種不同網(wǎng)格下粒子游動速度隨時(shí)間變化的計(jì)算結(jié)果,兩者吻合較好,驗(yàn)證了網(wǎng)格收斂性.以下研究所有工況均采用網(wǎng)格步長h=1/16.
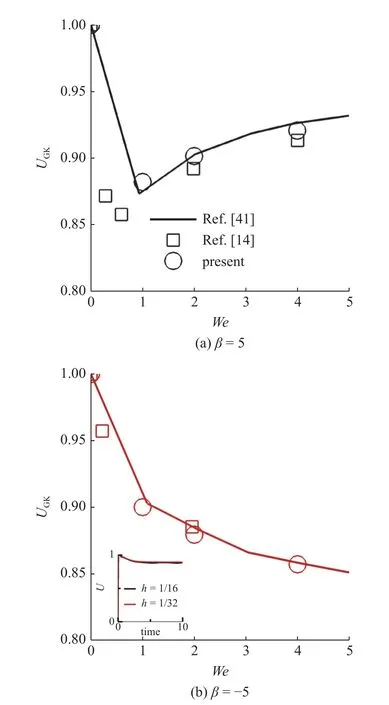
圖3 兩種類型粒子游動平均速度 UGK 隨 W e 變化規(guī)律: (a) β=5,(b) β=?5.(b)插圖為 β=?5,We=2 工況下粒子游動速度 U 隨時(shí)間的變化曲線;黑色實(shí)線為粗網(wǎng)格 h=1/16,?t=0.000 5 計(jì)算結(jié)果,紅色實(shí)線為細(xì)網(wǎng)格 h=1/32,?t=0.000 25 計(jì)算結(jié)果Fig.3 The average swimming speed UGK of squirmers: (a) β=5,(b) β=?5.Inset: squirmer swimming speed computed when using two different meshes at β=?5,We=2 ;black solid line represents the result of coarse grid h=1/16,?t=0.000 5,and the red represents the result of fine grid h=1/32,?t=0.000 25
3 結(jié)果與分析
本節(jié)將主要考察微生物在黏彈性流體中游動的壁面效應(yīng),重點(diǎn)探索近壁處微生物的行為特征以及相關(guān)的水動力機(jī)理,以期能夠初步得到微生物在復(fù)雜流體中游動的變化規(guī)律.
微生物游動問題屬于低Reynolds 數(shù)范疇,因此本節(jié)研究設(shè)定Re=0.01.在此基礎(chǔ)上,著重研究流體彈性性質(zhì)對微生物行為的影響規(guī)律,選取典型的Weissenberg 數(shù)范圍We=0 ~4.微生物模型選取兩種典型粒子 β=3,?3.其他參數(shù)如下: α=0.2,μr=0.5,ρr=1.0;計(jì)算區(qū)域大小為 [ 0,16]×[0,16]×[0,16],網(wǎng)格步長h=1/16,典型時(shí)間步長為 ?t=0.000 5 ~0.001.計(jì)算區(qū)域方向y為壁面無滑移邊界條件,其余兩個(gè)方向均為周期性邊界條件.粒子初始狀態(tài)如圖4 所示,初始位置位于z=0平面,粒子質(zhì)心與壁面初始距離d=2,初始游動方向與x軸夾角 γ=?π/4.
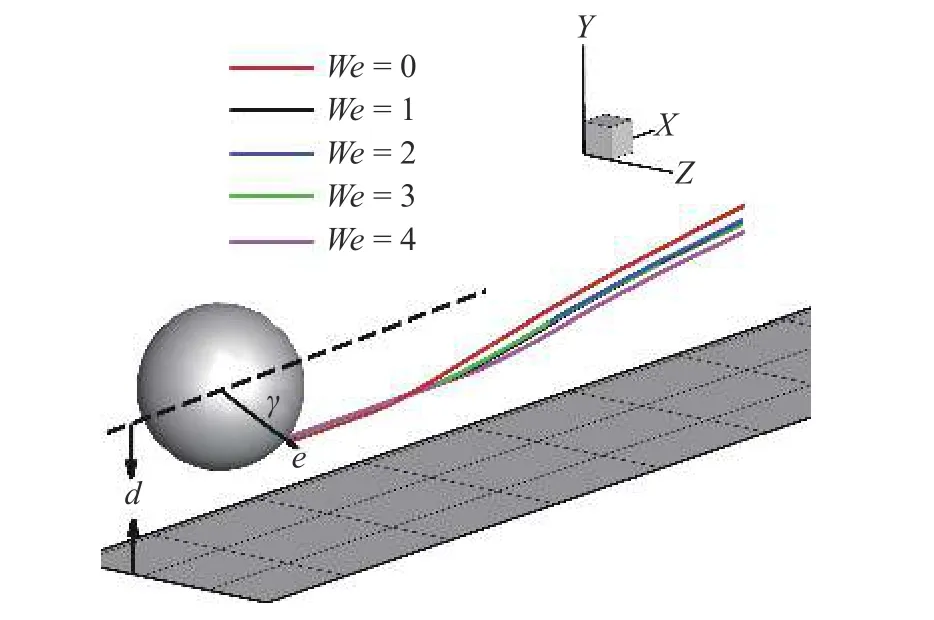
圖4 微生物顆粒(β=3)與壁面作用軌跡圖,粒子與壁面初始距離d=2,游動方向與 x 軸夾角 γ=?π/4Fig.4 Trajectory of puller (β=3) contact with wall,the initial distance between particles and wall d=2,the angle between swimming direction and x -axis γ=?π/4
首先,給出這兩種類型粒子自由游動狀態(tài)下周圍的流場結(jié)構(gòu).工況參數(shù)如上,但計(jì)算區(qū)域三個(gè)方向均為周期性邊界條件.如圖5 所示,隨體坐標(biāo)系下,黏彈性流體(We=4)中兩種類型粒子周圍流場結(jié)構(gòu)與牛頓流體(We=0) 類似.拉動型粒子(β=3)在尾部出現(xiàn)回流區(qū),推動型粒子( β=?3)則出現(xiàn)在頭部.與牛頓流體相比,黏彈性流體中流場速度較小,這與文獻(xiàn)[14,41]結(jié)論一致.背景云圖表示構(gòu)型張量的跡 T r(C)=c11+c22+c33.如圖5(b)所示,其極大值區(qū)域出現(xiàn)在推動型粒子尾部,表明該種粒子對尾部區(qū)域流體有很強(qiáng)的剪切作用.而拉動型粒子則是對粒子中部兩側(cè)區(qū)域有較強(qiáng)的剪切作用.
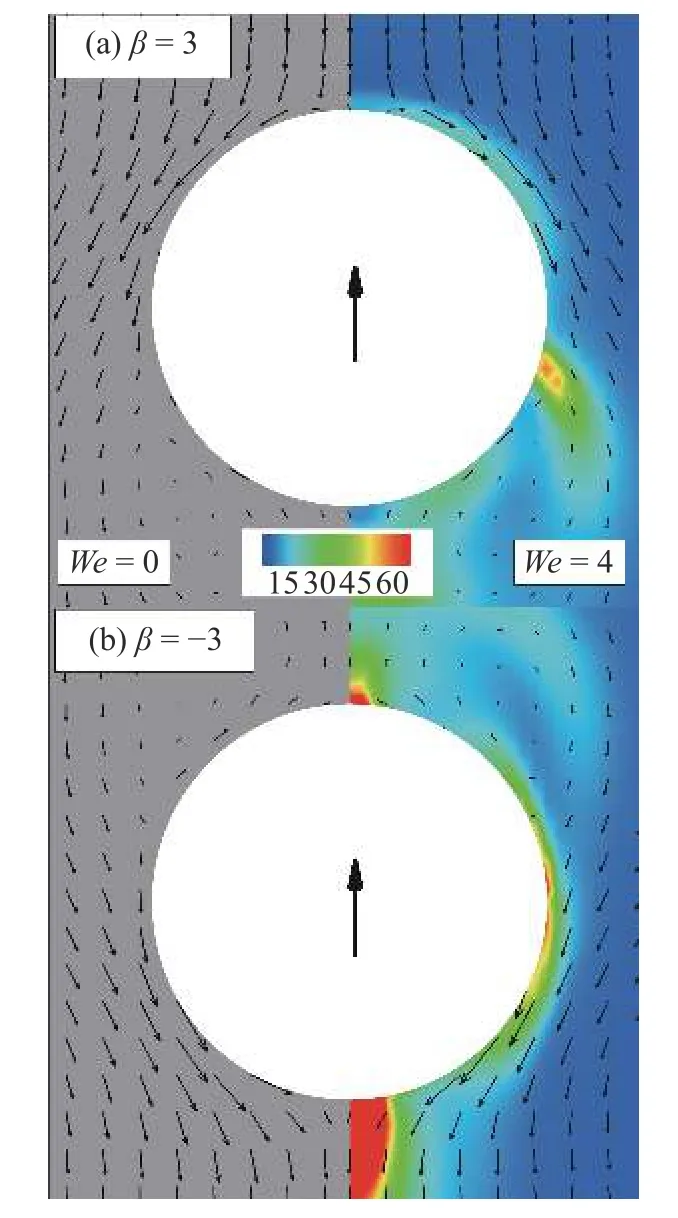
圖5 微生物顆粒自由游動流場結(jié)構(gòu)圖.坐標(biāo)系為隨體坐標(biāo);黑色箭頭表示顆粒游動方向,背景云圖表示構(gòu)型張量的跡 T r(C).左半部分圖為 W e=0 結(jié)果;右半部分圖為 W e=4 結(jié)果Fig.5 Flow field around squirmer particles free swimming in viscoelastic fluids with comoving frame;the black arrow represents the swimming direction of particles,and the background cloud chart represents the trace of the configuration tensor T r(C).The left part of figure shows the result at W e=0 ;the right part shows the result at We=4
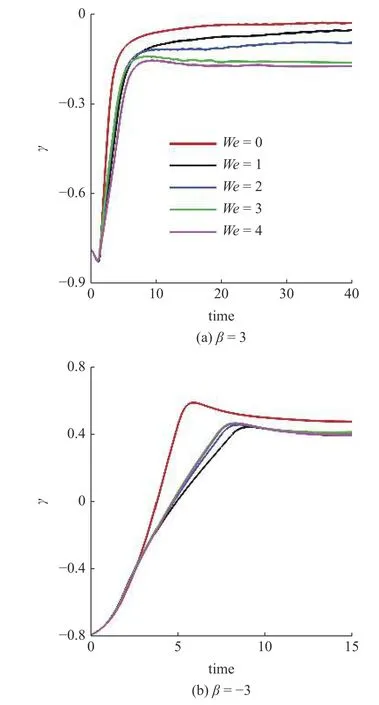
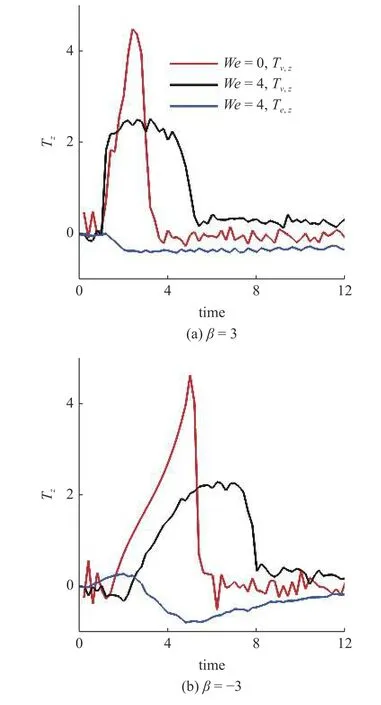
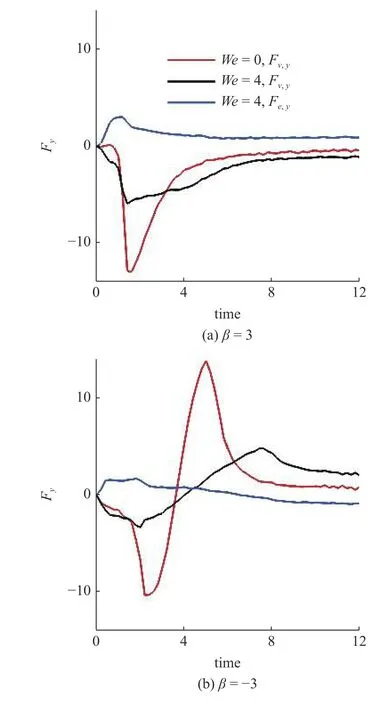
在此基礎(chǔ)上,研究黏彈性流體中微生物游動的壁面效應(yīng).圖6(a)~圖6(b)給出了兩種微生物顆粒與壁面間隔距離d隨時(shí)間發(fā)展的結(jié)果.對于拉動型粒子,在牛頓流體中,粒子與壁面充分接觸之后逃離壁面.在黏彈性流體中,則有所不同.隨著流體彈性增強(qiáng),當(dāng)We>2時(shí)拉動型粒子被壁面吸引,在壁面附近運(yùn)動并與壁面保持一定的間隔距離,其軌跡如圖4 所示.而對于推動型粒子,在兩種流體中均逃離壁面.這里必須指出,上述結(jié)果與文獻(xiàn)[14]的結(jié)論不盡相同.他們的結(jié)果表明隨著流體彈性性質(zhì)增強(qiáng),微生物顆粒更容易被壁面吸引,這一點(diǎn)與本文結(jié)論一致.不同之處在于Re=0.1工況下,黏彈性流體中推動型粒子被困在壁面附近,而拉動型粒子則能夠逃離壁面.可以認(rèn)為這與流體慣性相關(guān).文獻(xiàn)[15]的結(jié)果表明,在冪律流體中流體慣性改變(Re=0.1 ~0.5),導(dǎo)致推動型粒子在近壁處由被壁面吸引住轉(zhuǎn)變?yōu)樘与x壁面.Li 等[31-32]另外的研究工作指出牛頓流體中流體慣性影響微生物的行為特征.他們的結(jié)果表明,隨著Reynolds 數(shù)的增加(Re=0.1 ~1.0),微生物可以在逃離壁面和困在壁面兩種狀態(tài)轉(zhuǎn)換[32];甚至在Re=50工況下,微生物顆粒的游動出現(xiàn)不穩(wěn)定性,呈現(xiàn)復(fù)雜的三維行為特征[31].這些結(jié)果表明流體慣性對微生物的運(yùn)動特性具有復(fù)雜影響;需要進(jìn)一步研究.最后給出微生物顆粒與壁面的接觸時(shí)間,接觸判斷標(biāo)準(zhǔn)為d 圖6 不同類型微生物顆粒與壁面間隔距離 d 隨時(shí)間變化曲線.黏彈性流體的參數(shù)為: R e=0.01,W e=0 ~4,α=0.2,μ r=0.5,ρr=1.0Fig.6 The distance between squirmer particles and the wall in the y direction as a function of time.Parameters of viscoelastic fluid:Re=0.01,W e=0 ~4,α=0.2,μ r=0.5,ρr=1.0 對于上述現(xiàn)象,可以認(rèn)為與微生物顆粒的游動方向有關(guān).圖7 給出粒子游動方向與x軸的夾角隨時(shí)間發(fā)展的結(jié)果.在牛頓流體中,經(jīng)過與壁面接觸之后,拉動型粒子游動方向調(diào)整為與x軸幾乎平行.而在黏彈性流體中,其方向則明顯傾向壁面,因此粒子保持向壁面游動,無法逃離壁面.對于推動型粒子,如圖7(b)所示,夾角 γ由初始角度 ? π/4 發(fā)展為接近 π/8,表明粒子的游動方向由傾向壁面發(fā)展為遠(yuǎn)離壁面,與其行為特征吻合. 圖7 微生物顆粒游動方向與 x 軸夾角隨時(shí)間變化曲線.黏彈性流體的參數(shù)為: R e=0.01,W e=0 ~4,α=0.2,μ r=0.5,ρr=1.0Fig.7 Angle between squirmer particles swimming direction and the x -axis as a function of time.Parameters of the viscoelastic fluid:Re=0.01,W e=0 ~4,α=0.2,μ r=0.5,ρr=1.0 為了進(jìn)一步探討其背后的水動力機(jī)理,可以對微生物顆粒進(jìn)行動力學(xué)分析.圖8 給出粒子在x?y平面內(nèi)受到的水動力轉(zhuǎn)矩Tz;圖9 給出粒子受到的壁面垂直方向水動力Fy.兩者計(jì)算公式如下 圖8 微生物顆粒在 x ?y 平面內(nèi)受到的水動力轉(zhuǎn)矩 T z 隨時(shí)間變化曲線.其中,T v,z 表示黏性轉(zhuǎn)矩 z 方向分量,T e,z 表示彈性轉(zhuǎn)矩 z 方向分量,計(jì)算公式見式(33).黏彈性流體的參數(shù)為: R e=0.01,W e=0,4,α=0.2,μ r=0.5,ρr=1.0Fig.8 Hydrodynamic torque in the z direction computed using Eq.(33).Tv,z represents the viscous torque and T e,z the elastic torque.Parameters of the viscoelastic fluid: R e=0.01,W e=0,4,α=0.2,μ r=0.5,ρ r=1.0 這里選取We=0,4兩種典型的工況進(jìn)行分析.由圖8(a)可以看出,近壁處,黏性應(yīng)力產(chǎn)生的轉(zhuǎn)矩Tv,z>0,呈現(xiàn)逆時(shí)針方向,促使拉動型粒子游動方向遠(yuǎn)離壁面;而彈性應(yīng)力則相反,轉(zhuǎn)矩Te,z<0,呈現(xiàn)順時(shí)針方向,促使粒子游動方向傾向壁面.對于推動型粒子,如圖8(b)所示,黏性應(yīng)力產(chǎn)生更大的轉(zhuǎn)矩,使得粒子游動方向遠(yuǎn)離壁面,從而導(dǎo)致粒子能夠逃離壁面.這表明游動方向是影響微生物顆粒壁面效應(yīng)的重要因素.彈性應(yīng)力對游動方向的調(diào)制作用是黏彈性流體中微生物被壁面吸引的重要機(jī)理. 圖9 給出微生物顆粒受到的壁面垂直方向水動力.在壁面附近區(qū)域,黏性應(yīng)力Fv,y<0,對微生物顆粒呈現(xiàn)吸引作用,促使粒子向壁面運(yùn)動;而彈性應(yīng)力Fe,y>0,呈現(xiàn)排斥作用,促使粒子遠(yuǎn)離壁面.隨著時(shí)間發(fā)展,如圖9(b)所示,推動型粒子受到的黏性應(yīng)力變排斥作用;而彈性應(yīng)力則變?yōu)槲饔?這個(gè)轉(zhuǎn)變過程與推動型粒子游動方向由傾向壁面(γ <0)轉(zhuǎn)變?yōu)檫h(yuǎn)離壁面(γ >0)相吻合,我們認(rèn)為與此有關(guān). 圖9 微生物顆粒在壁面方向受到的水動力 F y 隨時(shí)間變化曲線.其中,F v,y 表示黏性應(yīng)力 y 方向分量,F e,y 表示彈性應(yīng)力 y 方向分量,計(jì)算公式見式(33).黏彈性流體的參數(shù)為: R e=0.01,W e=0,4,α=0.2,μ r=0.5,ρr=1.0Fig.9 Hydrodynamic forces in the y direction computed using Eq.(33).Fv,y represents the viscous force and F e,y the elastic force.Parameters of viscoelastic fluid: R e=0.01,W e=0,4,α=0.2,μ r=0.5,ρr=1.0 本文采用基于虛擬區(qū)域法,結(jié)合喬列斯基分解的數(shù)值方法,研究黏彈性流體中微生物游動問題.對于黏彈性流體本構(gòu)方程的求解: (1)構(gòu)型張量采用喬列斯基分解為一個(gè)上三角矩陣與一個(gè)下三角矩陣的乘積,并對對角線元素采用指數(shù)函數(shù)替換,從而在理論以及計(jì)算方面保證構(gòu)型張量的對稱正定性質(zhì);(2)對流項(xiàng)采用高精度的MUSCL 格式離散;(3)本構(gòu)方程采用顯式求解,時(shí)間積分采用四階龍格庫塔方法. 本文將上述方法初步應(yīng)用于研究微生物游動中的壁面效應(yīng).結(jié)果表明,游動方向是影響微生物顆粒壁面效應(yīng)的重要因素.彈性應(yīng)力對游動方向的調(diào)制作用是黏彈性流體中微生物被壁面吸引的重要機(jī)理.我們發(fā)現(xiàn): (1)對于拉動型微生物顆粒,Weissenberg數(shù)較大的工況下(We>2),流體彈性應(yīng)力產(chǎn)生一個(gè)反向轉(zhuǎn)矩,使得其游動方向顯著傾向壁面,從而阻礙微生物逃離壁面;(2)兩種類型粒子在黏彈性流體中與壁面作用時(shí)間較長,幾乎達(dá)到牛頓流體的兩倍以上;(3)近壁處,彈性應(yīng)力對兩種類型粒子呈現(xiàn)排斥作用,而黏性應(yīng)力則呈現(xiàn)吸引作用. 未來將在本文基礎(chǔ)上,進(jìn)一步研究黏彈性流體中微生物與復(fù)雜界面的相互作用以及近壁處微生物的行為特征,嘗試揭示其中的動力學(xué)機(jī)理以及變化規(guī)律,為微型器件的設(shè)計(jì)制造提供理論指導(dǎo). 數(shù)據(jù)可用性聲明 支撐本研究的科學(xué)數(shù)據(jù)已在中國科學(xué)院科學(xué)數(shù)據(jù)銀行ScienceDB 平臺公開發(fā)布,訪問地址為https://www.doi.org/10.57760/sciencedb.j00140.00009.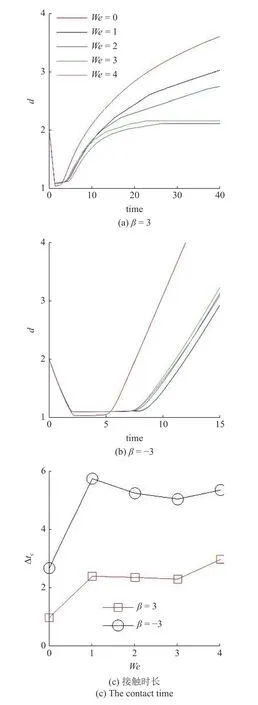
4 結(jié)論

