露天礦卡車SA-GA算法實時調度的實現

郭天中，郝靜

（包頭職業技術學院 材料工程系，內蒙古 包頭 014010）

0 引言

卡車運輸作為露天礦開采中最為主要的生產環節，其能否得到合理的調度直接影響著露天礦開采的生產效率，若卡車調度不合理容易造成其它環節的等待或不協調問題而浪費時間、降低經濟效益。本文在對露天礦開采實際調研的基礎上，充分分析了卡車運輸過程中的各個環節，采用計算機技術和人工智能算法對十分復雜的卡車調度系統進行研究，并最終應用模擬退火算法和遺傳算法相結合的方法動態地搜索卡車與挖掘機、破碎站之間的最佳組合，力求降低露天礦生產運輸的經濟成本。

1 SA-GA算法與GA算法搜索能力比較

1.1 TSP問題描述及算法的實現

TSP（Traveling Saleman Problem）問題即旅行商問題，它是一個涵蓋廣泛應用背景和重要理論價值的組合優化問題，其已被證明是一個經典的NP難題。與卡車調度的問題具有相似之處，因此以此對比GA算法與SA-GA算法的性能。

TSP問題可以描述為：已知m個城市之間的相對距離，一名旅行者由某一個城市出發遍歷這m個城市且每個城市僅訪問一次，而且最終必須返回出發的城市，求如何安排這些城市的訪問次序能夠使得旅行者行走的距離最短。

其數學模型描述如下：設一組城市集合M={m1，m2，…，mn}，其中任意2個城市mi、mj∈M間的距離為D（mi，mj），求解一條經過所有城市且僅經過一次的路徑（mp（1）,mp（2）,mp（3））使得式（1）值最小。

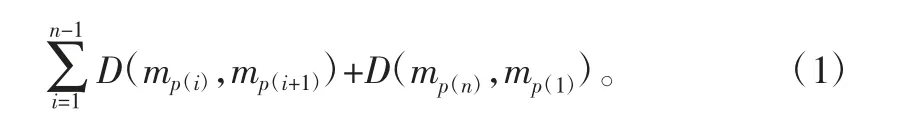
式中，（p(1),p(2),…，p(n)）為1,2,3…，n的一個置換。

1.2 實驗結果的比較與分析

對于上節所述的TSP問題，應用所述的編碼方式及參數設置方式，由Matlab軟件分別編制遺傳算法和改進的模擬退火遺傳算法程序，并對隨機生成的30個城市地點的TSP問題進行尋優，其中30座城市的坐標位置如表1所示。

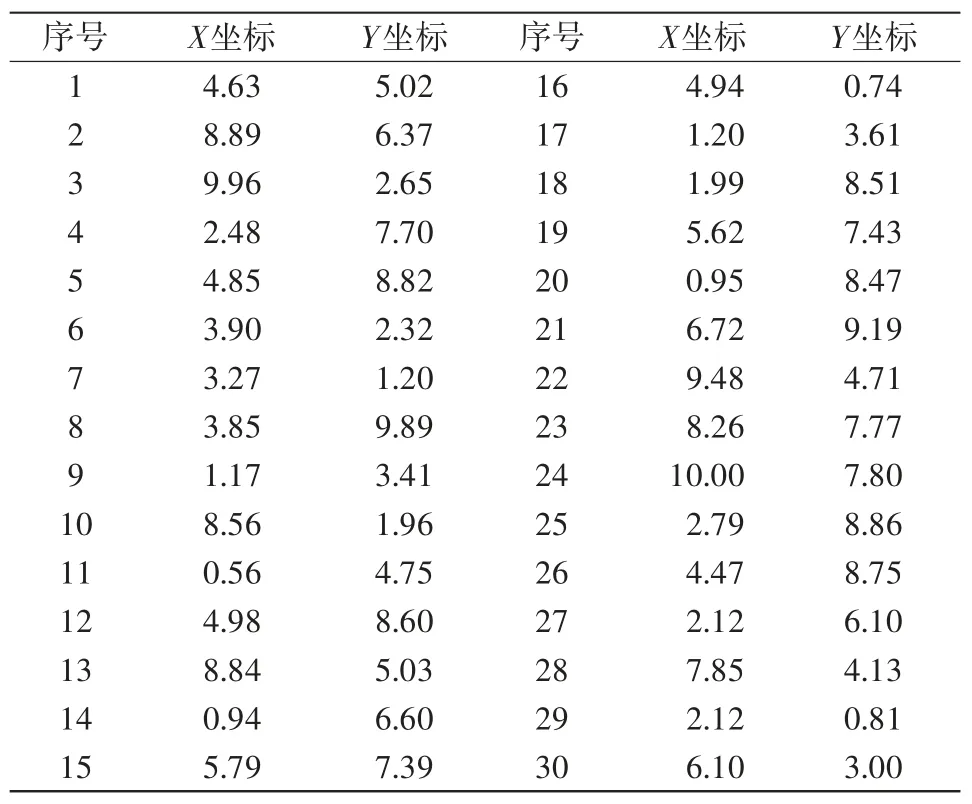
表1 30座城市坐標

30座城市的位置分布如圖1所示。

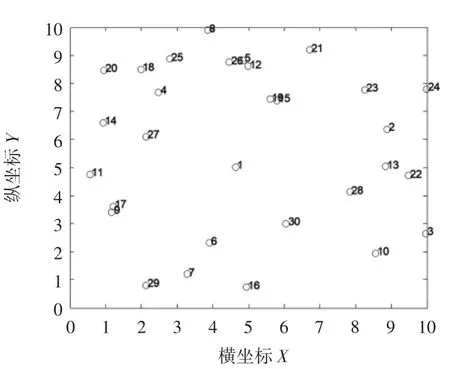
圖1 30座城市的位置分布圖

對于編制的遺傳算法程序和模擬退火算法程序分別在配置為Intel Core（TM）i5-2520 CPU@2.50 GHz、內存為2.00 GB的32位Win7操作系統中運行。

首先應用遺傳算法尋找最佳路徑。

在遺傳算法尋優時，首先初始種群中的一個隨機路徑為：20→18 →27 →4→7→19→3→24→30→17→10→5→25→11→6→9→13→1→8→22→12→21→14→15→16→2→26→28→29→23→20。其表示由城市20開始出發一次經過城市18，城市27，如此類推，直至回到出發城市20，總距離為161.308 2。其路徑軌跡圖如圖2所示。

圖2 GA算法初始種群隨機路徑

然后，由遺傳算法進行迭代尋優，經多次迭代最終獲得的最優路徑為：11→17 →9 →29 →7 →6 →16 →30→28→10→3→22→13→2→24→23→21→12→5→26→8→25→18→20→4→19→15→1→27→14→11。

其獲得的最優路徑圖如圖3所示。最終獲得的尋優路徑的總距離為47.689 5。比此前隨機生成路徑的總距離161.308 2縮短了許多，其具體優化過程曲線如圖4所示。從圖4中可以看出，GA算法前期迭代過程比較緩慢，局部搜索能力較弱且在近140代前就收斂至最優解。

圖3 GA尋優路徑軌跡圖

同樣由模擬退火算法與遺傳算法結合的SA -GA 算法對上述的30座城市的最佳路徑進行尋優。起初同樣隨機生成初始種群中的一個隨機值為：22 →1 →24 →8 →9 →30 →21 →4 →13 →6 →20 →25 →14 →17 →26 →18 →11 →2 →29 →19 →23→3→16→7→15→5→27→10→12→28→22；其隨機生成路徑的總距離為154.128 4，其具體路徑軌跡圖如圖5所示。

圖4 GA算法尋優迭代過程

圖5 SA-GA算法初始種群隨機路徑

根據模擬退火和遺傳算法的各個參數，然后由SA-GA算法尋得的最佳路徑的最優解為：13→22 →3 →10 →28 →30 →1 →6 →16 →7 →29 →9 →17 →11 →14 →27→4→20→18→25→8→26→5→12→19→15→21→23→24→2→13。

最終總距離為45.533 7，其具體尋優路徑軌跡如圖6所示。同樣比SA-GA算法隨機生成的路徑距離154.128 4小，比由GA算法尋得的最優路徑的總距離47.689 5也小。且將SA-GA算法的優化過程曲線（如圖7）與GA算法優化曲線（如圖4）相比可知，SA-GA算的局部搜索能力更強，而且前期收斂迅速，后期收斂緩慢，最終在近160代左右收斂。以優化算法的評價指標進行評價，對GA算法與SAGA算法各運行10次求得的各項評價指標如表2所示。其中時間性能指標直接求取10次運行結果的平均值，其值越小，運行時間越短。由表1可以看出優化性能和魯棒性SA-GA算法均優于GA算法，優化性能和魯棒性能值越小越好，因此盡管SA-GA算法在運行時間上略長于GA算法,但在優化性能和魯棒 性 上SA-GA算法均優于GA算法。

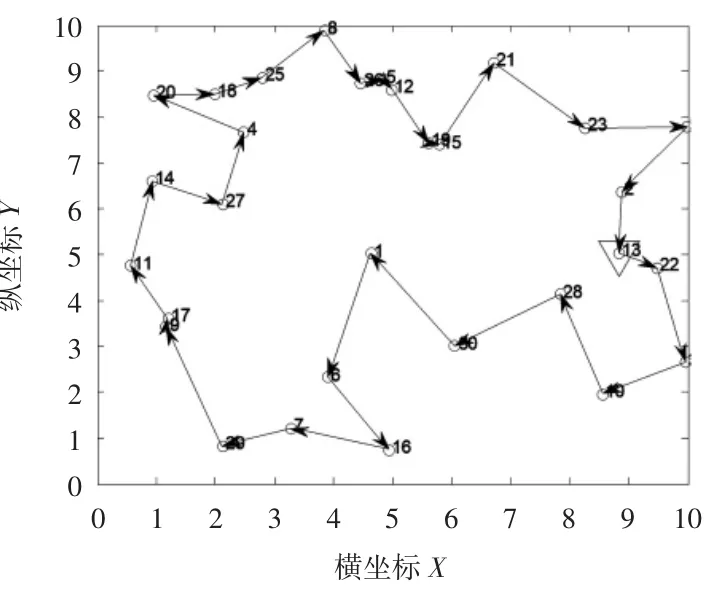
圖6 SA-GA尋優路徑軌跡圖

圖7 GA算法尋優迭代過程

表2 GA算法與SA-GA算法性能比較

由此可得，將SA算法與GA 算法結合起來的SA-GA算法無論是從最終的優化結果還是優化過程中的搜索能力都比單純的GA算 法 優越，因此將SA-GA算法應用到露天礦用卡車的調度過程中將能夠獲得更優的結果。

2 哈爾烏素露天礦卡車的SA-GA實時調度的實現

2.1 哈爾烏素露天礦開采狀況

哈爾烏素露天煤礦是我國自行設計并施工的特大型露天煤礦，位于準格爾煤田中部，可采原煤儲量達14.98億t，設計生產能力為每年2000 萬t。其開采選用的主要設備許多都是從國外引進的當今最先進的采礦設備，包括1臺P&H公司2800型電鏟及日本小松德萊賽630E型154 t電動輪自卸卡車58臺等設備。同時其調度管理系統采用的是由某公司提供的露天煤礦GPS智能礦山管理系統，其系統能夠通過采用全球衛星定位技術（GPS）、計算機及網絡技術、無線數字通信技術、礦山系統工程及優化理論、地理信息系統技術（GIS）、電子技術等高新技術對傳統的人工調度系統及管理體制進行改造，通過采集生產設備動態信息，實時監控和優化調度卡車、電鏟、輔助設備等設備的運行。在其車輛智能調度模塊中為了實現車輛智能調度，其采用的流程如圖8所示。

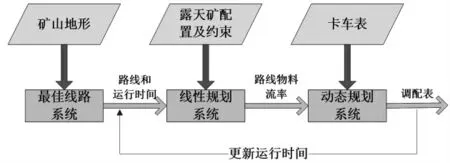
圖8 智能調度系統流程

最佳線路子系統能夠根據礦山地形計劃出相對兩點間的最短路徑；而線性規劃子系統采用最佳線路子系統生成的運行時間和最優路徑，以及當前露天坑內配置的信息：如可用于作業的電鏟和卡車的數量，在電鏟和卸載點的裝載時間和卸載時間，在相應卸載點和破碎站的配礦要求及電鏟的優先權。然后建立線性規劃的約束條件。該模型的最終解是優化的最佳路線的貨流量，在坑內配置既定時，使卡車運輸需求量最少。最后，動態規劃子系統利用線性規劃的結果，申請分派指令（由卸載點至電鏟）的卡車名單，當前的運行時間和運輸距離，為每臺卡車生成一個最優的實時調度表。每當卡車請求分派指令時，調用動態規劃程序，生成一個按照需求排序的由卸載點至電鏟的路徑表，并將卡車分派給各條路徑。最后，系統運用滑動平均值更新運輸時間。

智能調度采用兩階段模型法進行：首先，根據班計劃及生產的進行情況對通往各裝載點、卸載點的車流進行車流規劃；然后，在卡車需要調度時，根據生產的實際情況以車流規劃為基礎進行實時調度。

由前述可知，動態規劃雖然具有一定的優點，但其不足是動態規劃模型沒有統一的標準模型，而且求解時存在維數災難。而智能算法恰恰能夠克服其不足，在組合優化方面和車輛調度領域應用廣泛。因此，本節針對智能調度系統中的動態規劃系統應用SA-GA算法進行替換，以此獲得更優的實時調度效果。

2.2 基于SA-GA算法露天礦卡車調度系統實現

針對影響露天礦生產效率的采運設備調配的特點及現在使用的露天煤礦GPS智能礦山管理系統的不足，本文編寫了基于SA-GA算法露天礦卡車調度系統，實現對卡車的實時調度。該系統能夠隨著采運設備參數的變化而重新尋優，如當增減卡車數量或改動卡車一些參數；增減破碎站數量或改動其一些參數；增減挖掘機數量或改動其一些參數；修改各站點之間的距離等。該程序能夠由修改后的數據再次尋優，從而計算出設定時間段內的卡車調度安排表。

2.2.1 基于SA-GA算法露天礦卡車調度系統的主流程

卡車調度系統包括主程序和一些子程序。系統中，主程序的主要功能包括：首先判斷程序是否為第一次調用該系統程序。若是，主程序就會調用初始化數據子程序對數據進行初始化；若不是，則會調用最近一次優化結果。然后，便調用計時程序對優化時刻進行實時監控，若到達程序優化時刻，則調用優化子程序，對卡車路徑下一時間段卡車最優調度路徑進行安排，并給出卡車進度時刻及調度安排的甘特圖，接著調用數據調整程序，為下次卡車路徑優化準備初始數據；否則就會一直計時，直到達到下次優化時刻。此外，當運輸過程中設備調整（如增減卡車、挖掘機、破碎站數量或更改設備的某些參數）后會調用調整后的數據處理程序，由此獲得調整后的計算所需要數據，然后再調用路徑優化程序獲得設備調整以后的卡車最優調度路徑。

主程序的流程如圖9所示。由圖9可知，促使調入卡車路徑優化程序的具有兩種條件，分別是到了規定的優化時刻，再者是優化過程中調整設備。每次運行SA-GA 優化程序后，就會獲得每輛卡車對應的破碎站和挖掘機的甘特圖及到達時刻表。

圖9 主程序流程圖

2.2.2 各程序功能及實現

基于SA-GA算法的露天礦卡車調度程序的主程序、子程序的主要功能如下：

1）主程序（Main）主要功能是：判定系統程序是否被第一次使用；連接各個子程序并最終給出卡車調度的路徑。

2）初始數據子程序（InitialData）主要功能是：第一次調用系統程序時設定的基本數據，包括遺傳算法的一些基本參數和調度設備的一些參數。

3）卡車路線產生子程序（ProduceRoute）主要功能是：產生最初的一條卡車路線并記錄下由此產生的費用及挖掘機和破碎站的任務狀態。

4）種群初始化子程序（Initalition）主要功能是：初始化染色體并計算出相應的適應度值（即相應的調度方案費用）及到達破碎站和挖掘機的時刻及它們狀態變化。

5）優化子程序（Optimize）主要功能是：按照SA-GA算法流程圖完成規定時間內中現有設備條件下的卡車調度路徑的尋優，給出最佳的卡車調度結果。有關模擬退火和遺傳算法的基本參數如表3、表4所示。

表3 遺傳算法參數設定

表4 模擬退火參數設定

6）各類設備狀態調整子程序。其中：增加卡車子程序（Add_Truck）的主要功能是給新增卡車編號，確定起始站點，設定卡車的各種參數并啟動卡車路徑優化子程序；卡車參數修改子程序(Amend_Truck)主要功能是找出卡車編號對應的卡車，修改相關參數（如卡車速度、容量、各種費用）；卡車刪除子程序（Delete_Truck）主要功能是刪除相應編號卡車的所有信息；增加挖掘機子程序（Add_Excavator）主要功能是將挖掘機編號并將其編排到挖掘機狀態矩陣中并啟動重新優化卡車路徑子程序；挖掘機參數修改子程序(Amend_Excavator)主要功能是找出預修改的挖掘機編號，修改挖掘機與破碎站之間的距離，修改挖掘機的工作效率；挖掘機刪除子程序（Delete_Excavator）找出預刪除的挖掘機編號并刪除所有相關參數；增加破碎站子程序（Add_Crush）主要功能是將破碎站編號，給定其到各個挖掘機站點的距離，給出破碎站的工作效率，激發卡車路徑優化子程序；破碎站參數修改子程序(Amend_Crush)主要功能是找出預修改的破碎站并修改相應參數；破碎站刪除子程序（Delete_Crush）主要功能是找出預刪除的破碎站并刪除相應參數。

7）計時子程序（TimeLong）主要功能是計算出兩個卡車調度間的時間長度。其實現過程是以開始優化時的電腦時刻開始計時，其計時格式為年、月、日、時、分、秒，每當卡車完成一次運輸過程其就會記錄下每個節點的時刻。

8）時刻比較子程序（CompareTime）主要功能是比較多輛卡車往返于挖掘機與破碎站之間時刻的先后順序。其實現過程是對于記錄的兩個時刻t1和t2進行比較，若經過比較結果為0，則t1先到；若比較結果為1，則t2先到。

對于以上主程序及子程序，結合前述建立的露天礦卡車調度模型，應用Matlab編制并實現主程序和各個子程序。對于基于SA-GA算法的露天礦卡車調度系統實際應用中涉及到的主要設備參數如下。

1）優化時間間隔。由露天礦實際開采情況可知，采掘點和一些設備是不斷變化的，其只能在一定時間內保持不變，因此在實際使用系統程序時優化時間間隔，可以根據實際生產狀況設定，可以是1 h、8 h等。

2）卡車載重和挖掘機工作效率。由此便能夠計算出正常工作條件下，挖掘機裝滿卡車所需要的時間。

3）挖掘機到破碎站之間的距離。距離矩陣如下：

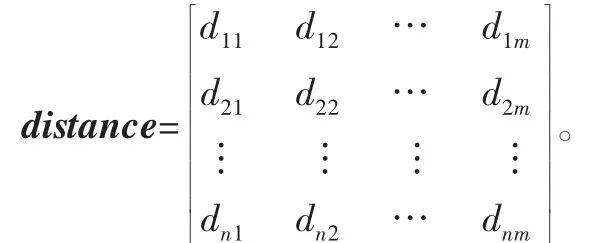
式中：矩陣的行數為挖掘機的數量n；列數為破碎站的數量m；dij（其中i=1，2，…，n；j=1，2，…，m）表示挖掘機i到破碎站j的距離。在實際生產中，盡管挖掘機到破碎站之間的距離一定，但由于不同道路間的路面質量、坡度不同，卡車在運行時的速度也不同，為了平衡由此帶來的影響，在給定它們之間的距離時，根據其影響大小折算為適當的距離。

4）卡車速度。包括卡車重載時的速度和空載時的速度，其可表示為

式中：t為卡車的數量；第一列vi1（i=1，2，…，t）為重載時的速度；第二列vi2為空載時的速度。

5）運輸費用。包括卡車重載時的費用、空載時的費用及維修時的費用，其可表示為

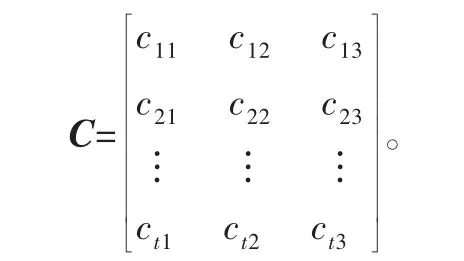
式中：t為卡車的數量；第一列ci1（i=1，2，…，t）為重載時的卡車運輸的費用；第二列ci2為空載時卡車運輸的費用；第三列ci3為卡車的維修費用。

2.3 基于SA-GA算法露天礦卡車調度實例

針對哈爾烏素露天礦某一開采區2014年12月份某一工作日的開采數據應用基于SA-GA算法的調度程序進行調度。在此開采區投入使用的設備情況為20輛卡車、12臺挖掘機和3臺破碎機。卡車和挖掘機設備的參數如表5、表6所示。

表5 卡車參數

表6 挖掘機參數

其中卡車的速度根據采掘工藝要求空載時不高于40 km/h，重載時不低于30 km/h。因此在應用程序時所有卡車空載的速度都設定為40 km/h，重載時都設定30 km/h。根據現場工人的開采經驗得到各型號卡車的運輸費用矩陣如下：MT5500B型的矩陣C1=[350 300 1.5]；MT4400AC型的矩陣C2=[260 200 1]；930-E型的矩陣C3=[320 260 1.5]；SF33900型的矩陣C4=[250 190 1]；HMTK600B型的矩陣C5=[390 330 2]。12臺挖掘機到3臺破碎站之間的距離矩陣為

在應用卡車調度程序時將20輛卡車分別命名為小寫字母a～t；3臺破碎站命名為a～c；12臺挖掘機分別命名為大寫字母A～L；并隨機選擇卡車出發點，程序調度間隔設定為1 h，對于以上數據逐步輸入基于SA-GA算法的卡車調度程序中并在配置為Intel Core （TM） i5 -2520 CPU@2.50GHz、內存為2.00 GB的32位WIN7操作系統運行，最終獲得20輛卡車的調度結果如圖10～圖12所示。

其中圖10為基于SA-GA算法露天礦卡車調度結果輸出頁面的截圖。以第一輛卡車的調度結果對其調度輸入結果解釋，第一臺卡車a在設備不變動的1 h內的運行路徑為：卡車a從2015年3月8日16時43分48.5秒開始由編號為A的挖掘機滿載出發將煤運至編號為c的破碎站，到達c破碎站的時刻是2015年3月8日16時59分19.7秒；接著出發到達編號為I的挖掘機進行裝煤，達到挖掘機I的時刻為2015年3月8日17時4分20.9秒，然后又將煤運至破碎站c，此時的時刻為2015年3月8日17時20分38.9秒；接著卡車又跑至編號為F的挖掘機處進行裝煤，此時的時刻為2015年3月8日17時28分2.9秒，然后又將煤運達破碎站c處卸載，此時的時刻為2015年3月8日17時42分43.7秒。至此卡車1 h 以內的調度路徑就被確定。為了能給工人師傅更直觀地顯示每輛卡車的調度進度和持續時間，卡車調度系統輸出了反映每輛卡車達到破碎站和挖掘機的時刻及持續時間甘特圖，其輸入結果如圖11所示。經過模擬退火優化遺傳算法對卡車調度的優化，此20輛卡車運輸費用的變化過程如圖12所示，從圖12中可以看出，卡車運輸費用起初較高，經過SA-GA算法的不斷優化，算法能夠較快地尋得最佳的卡車調度方案，最終獲得的在1 h內卡車調度方案總的運輸費用為52 747 元；對調度結果進行統計得20輛卡車共運送煤炭5158 t，行駛的總距離為214.4 km，由此便可得其噸公里運輸成本約為0.047 6 元/（t·km）。將此結果與此開采區運輸環節噸公里成本（2011年為1.014 9元/（t·km），2012年為0.972 9 元/（t·km））相比，基于SA-GA算法調度卡車的運輸成本較低，由此可得本文所提出的基于SA-GA算法的露天礦卡車調度方法能夠詳細地給出礦用卡車調度計劃和安排，為現場卡車實時調度提供了決策依據，能夠較好地指導實際生產，有利于企業降低生產成本，獲得更大的經濟效益。

圖10 基于SA-GA算法露天礦卡車調度結果

圖11 基于SA-GA算法卡車調度甘特圖

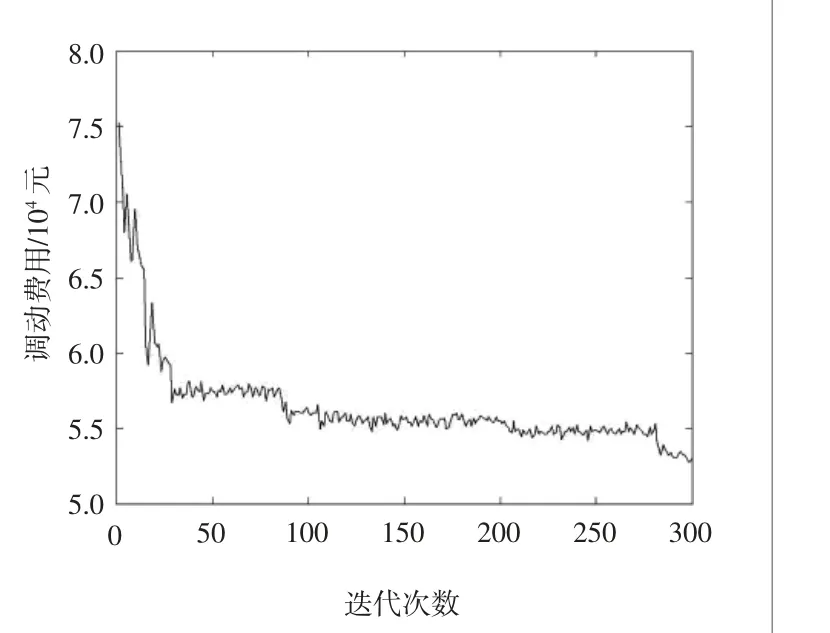
圖12 基于SA-GA算法卡車調度費用迭代過程

3 結論

針對本文提出的模擬退火優化遺傳算法的方法，首先應用與露天礦卡車調度具有相同數學背景的典型的優化組合問題——TSP問題對SA-GA算法和GA算法進行比較，結果證明本文提出的模擬退火優化的遺傳算法比單純的遺傳算法能夠獲得更優的全局最優解且魯棒性更好；接著對哈爾烏素露天礦現行的卡車調度系統中動態規劃調度方法中的不足，本文編制了基于SA-GA算法的露天礦用卡車調度程序，并詳述了各個程序的功能及實現過程；最后以哈爾烏素露天礦某開采區的采掘設備數據為例，采用SA-GA算法的露天礦用卡車調度程序對卡車進行了調度，調度結果不僅給出了1 h內每臺卡車的行駛路徑和時刻表，而且給出了總的運輸費用為200 元，由此得到噸公里成本為0.047 6 元/（t·km）, 比2011年的1.014 9元/（t·km）和2012年的0.972 9 元/（t·km）成本都低，降低了運輸成本，很好地指導了實際生產。